DOCSLIB.ORG

Bivariate Angular Estimation Under Consideration of Dependencies Using Directional Statistics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bivariate Angular Estimation Under Consideration of Dependencies Using Directional Statistics Bivariate Angular Estimation Under Consideration of Dependencies Using Directional Statistics Gerhard Kurz1, Igor Gilitschenski1, Maxim Dolgov1 and Uwe D. Hanebeck1 Abstract— Estimation of angular quantities is a widespread issue, but standard approaches neglect the true topology of the problem and approximate directional with linear uncertainties. In recent years, novel approaches based on directional statistics have been proposed. However, these approaches have been unable to consider arbitrary circular correlations between multiple angles so far. For this reason, we propose a novel recursive filtering scheme that is capable of estimating multiple angles even if they are dependent, while correctly describing their circular correlation. The proposed approach is based on toroidal probability distributions and a circular correlation coefficient. We demonstrate the superiority to a standard approach based on the Kalman filter in simulations. Fig. 1: A bivariate wrapped normal probability distribution Index Terms— recursive filtering, wrapped normal, circular on the torus shown as a heat map. correlation coefficient, moment matching. I. INTRODUCTION our knowledge, this is the first work on recursive estimation There are many applications that require estimation of based on toroidal probability distributions. angular quantities. These applications include, but are not It should be noted that there are some directional filters that, limited to, robotics, augmented reality, and aviation, as well in a sense, take correlation between angles into account. We as biology, geology, and medicine. In many cases, not just have performed research on a filter based on the hyperspheri- one, but several angles have to be estimated. Furthermore, cal Bingham distribution [8], [9], which captures correlations correlations may exist between those angles and have to be when estimating rotations represented as quaternions. A very taken into account in the estimation algorithm. For example, similar approach has independently been published by Glover there may be dependencies between the orientations of head et al. [10]. Furthermore, Feiten et al. have used mixtures of and torso of a person. Another example is a robot arm with projected Gaussians to deal with 6D pose estimation while several rotary joints that are affected by correlated noise. considering correlations between different angles as well as Traditional approaches for estimating correlated angles are correlation between position and orientation [11]. However, all typically based on Gaussian distributions and use classical of these approaches are intended for describing 3D rotations, filtering algorithms such as the Kalman filter [1] or nonlinear which have a different underlying topology, namely the group extensions thereof, e.g., the unscented Kalman filter [2]. SO(3) [12], rather than the torus. For this reason, they cannot However, Gaussian distributions are defined on n-dimensional be used to estimate arbitrary correlated angles. vector spaces rather than the proper manifold, in this case a In the field of directional statistics, some previous work on torus or hypertorus. toroidal distributions can be found. In particular, multivariate Some filtering algorithms that are particularly well-suited generalizations of the von Mises distribution have been for angular estimation have been proposed. They rely on studied by several authors [13], [14]. The multivariate periodic probability distributions that stem from the field wrapped normal distribution has also been considered [4, of directional statistics [3], [4]. For example, Azmani et Sec. 2.3.2], [15], which will be the foundation of the algorithm al. proposed a filtering algorithm based on the von Mises that we propose in this paper. Furthermore, various directional distribution [5], [6]. In our prior work, we proposed an versions of the correlation coefficient have been suggested. algorithm based on the wrapped normal distribution [7]. We use the circular correlation coefficient as defined in [4, However, these approaches are one-dimensional and unable Sec. 8.2] and [15]. to take correlations between several angles into account. To address this deficiency, we propose a new filtering II. TOROIDAL STATISTICS algorithm for estimation of correlated angles in this paper. To In this section, we give an introduction to toroidal statistics. 1 The authors are with the Intelligent Sensor-Actuator-Systems Laboratory First of all, we define the necessary topological spaces. The (ISAS), Institute for Anthropomatics and Robotics, Karlsruhe Institute of Technology (KIT), Germany (e-mail: [email protected], unit circle [email protected], [email protected], 1 [email protected]). S =fx 2 C : jjxjj = 1g =fcos(φ) + i sin(φ) : 0 ≤ φ < 2πg distribution with parameters µ and Σ. Note that the parameter matrix stems from the covariance of a bivariate normal is identified with the interval S1 ≡ [0; 2π), while keeping distribution, yet its meaning is different in the toroidal context. the topology in mind. The torus T 2 = S1 × S1 is obtained An example of the TWN distribution is depicted in Fig. 2a. as the Cartesian product of two circles. More generally, the It can be seen how x and x are 2π-periodic and the n-torus 1 2 distribution wraps at these locations. T n = S1 × · · · × S1 = (S1)n | {z } n times B. Toroidal Moments is obtained by the n-fold Cartesian product of circles. We In analogy to the traditional linear moments, we introduce only consider T 2 in the remainder of this paper. Most of the the circular moments and subsequently generalize them to presented techniques can be generalized to the n-torus. toroidal moments. A. Toroidal Distributions Definition 3 (Circular Moments). Before we look at the bivariate toroidal wrapped normal In the univariate case, the n-th circular moment (sometimes distribution, we introduce the circular univariate wrapped also referred to as trigonometric or angular moment) of a normal distribution to show how the toroidal distribution is a random variable x is given by generalization of the circular case. Z 2π inx inx Definition 1 (Wrapped Normal Distribution). mn = E(e ) = f(x)e dx 2 C ; A univariate wrapped normal (WN) distribution is given by 0 its probability density function (pdf) where i is the imaginary unit. 1 X Note that the n-th circular moment is a complex number, f(x; µ, σ) = N (x; µ + 2πj; σ) i.e., it has two degrees of freedom. The argument of m1 j=−∞ determines the location of the circular mean, whereas the 1 1 with x 2 S , location parameter µ 2 S , dispersion parameter absolute value of m1 determines the concentration. For this σ > 0, and normal density N (x; µ, σ). reason, a WN distribution is uniquely determined by its first circular moment. We generalize circular moments to the We use the notation X ∼ WN (µ, σ) to indicate that bivariate case in the following Definition. a random variable X is distributed according to a WN distribution with parameters µ and σ. A WN distribution Definition 4 (Toroidal Moments). is obtained by wrapping a normal distribution around the For a random variable x distributed according to a toroidal unit circle. The normalization constant is already included distribution, the n-th toroidal moment is given by in the Gaussian distributions, so it does not need to be inx1 Z 2πZ 2π inx1 calculated separately. This is a significant advantage compared e e 2 mn = E inx2 = f(x) inx2 dx1dx2 2 C : to other periodic probability distributions whose normalization e 0 0 e constants can be difficult to calculate. The WN distribution The n-th bivariate circular moment is a vector of two can be generalized to the bivariate case as follows. complex numbers, and thus, has four degrees of freedom. Definition 2 (Toroidal Wrapped Normal Distribution). Lemma 1 (Moments of a TWN distribution). The toroidal (or bivariate) wrapped normal (TWN) distribu- The n-th moment of TWN (µ; Σ) is given by tion is given by the pdf 1 1 " # " 2 2 # X X 2πj mn;1 exp(inµ1 − n σ =2) f(x; µ; Σ) = N x; µ + ; Σ m = = 1 ; 2πk n 2 2 j=−∞ k=−∞ mn;2 exp(inµ2 − n σ2=2) T 1 1 with x = [x1; x2] 2 S × S , location parameter µ = i.e., the componentwise circular moment of a WN (µ1; σ1) T 1 1 [µ1; µ2] 2 S × S , and symmetric parameter matrix and a WN (µ2; σ2). 2 σ1 ρσ1σ2 2×2 The proof is given in the appendix. Note that the n-th Σ = 2 2 R · σ2 bivariate circular moment does not depend on the linear correlation coefficient ρ. with correlation1 parameter −1 < ρ < 1, linear standard deviations σ ; σ > 0, and multivariate normal distribution 1 2 C. Circular Correlation Coefficient N (x; µ; Σ). Several circular correlation coefficients have been defined The notation X ∼ T WN (µ; Σ) is used to indicate that (for example by Mardia [16], Johnson [17], Jupp [18], and a random variable X is distributed according to a TWN Fisher [19]). We use the definition of Jammalamadaka et al. 1While the linear correlation coefficient ρ can reach values −1 and 1, [15], [4], because it is intuitive, easy to work with and has a we do not consider these cases because they lead to a positive semidefinite variety of nice properties (see [15, Theorem 2.1]). rather than a positive definite covariance matrix. 1 c 0.5 ρ 0 4 4 3 3 2 2 1 1 σ σ 2 0 0 1 (a) A bivariate wrapped normal probability distribution with (b) Circular correlation coefficient for a TWN distribution with T parameters µ = [1; 6] and Σ = [1; 0:5; 0:5; 1] Keep in mind given σ1; σ2 and ρ ! 1. As can be seen, the circular correlation that x1 and x2 are 2π-periodic. coefficient ρc is significantly lower than ρ for large σ1; σ2. Fig. 2: Toroidal wrapped normal distribution and circular correlation.
Load more

Recommended publications
  • Contributions to Directional Statistics Based Clustering Methods
    University of California Santa Barbara Contributions to Directional Statistics Based Clustering Methods A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Statistics & Applied Probability by Brian Dru Wainwright Committee in charge: Professor S. Rao Jammalamadaka, Chair Professor Alexander Petersen Professor John Hsu September 2019 The Dissertation of Brian Dru Wainwright is approved. Professor Alexander Petersen Professor John Hsu Professor S. Rao Jammalamadaka, Committee Chair June 2019 Contributions to Directional Statistics Based Clustering Methods Copyright © 2019 by Brian Dru Wainwright iii Dedicated to my loving wife, Carmen Rhodes, without whom none of this would have been possible, and to my sons, Max, Gus, and Judah, who have yet to know a time when their dad didn’t need to work from early till late. And finally, to my mother, Judith Moyer, without your tireless love and support from the beginning, I quite literally wouldn’t be here today. iv Acknowledgements I would like to offer my humble and grateful acknowledgement to all of the wonderful col- laborators I have had the fortune to work with during my graduate education. Much of the impetus for the ideas presented in this dissertation were derived from our work together. In particular, I would like to thank Professor György Terdik, University of Debrecen, Faculty of Informatics, Department of Information Technology. I would also like to thank Professor Saumyadipta Pyne, School of Public Health, University of Pittsburgh, and Mr. Hasnat Ali, L.V. Prasad Eye Institute, Hyderabad, India. I would like to extend a special thank you to Dr Alexander Petersen, who has held the dual role of serving on my Doctoral supervisory commit- tee as well as wearing the hat of collaborator.
    [Show full text]
  • Recent Advances in Directional Statistics
    Recent advances in directional statistics Arthur Pewsey1;3 and Eduardo García-Portugués2 Abstract Mainstream statistical methodology is generally applicable to data observed in Euclidean space. There are, however, numerous contexts of considerable scientific interest in which the natural supports for the data under consideration are Riemannian manifolds like the unit circle, torus, sphere and their extensions. Typically, such data can be represented using one or more directions, and directional statistics is the branch of statistics that deals with their analysis. In this paper we provide a review of the many recent developments in the field since the publication of Mardia and Jupp (1999), still the most comprehensive text on directional statistics. Many of those developments have been stimulated by interesting applications in fields as diverse as astronomy, medicine, genetics, neurology, aeronautics, acoustics, image analysis, text mining, environmetrics, and machine learning. We begin by considering developments for the exploratory analysis of directional data before progressing to distributional models, general approaches to inference, hypothesis testing, regression, nonparametric curve estimation, methods for dimension reduction, classification and clustering, and the modelling of time series, spatial and spatio- temporal data. An overview of currently available software for analysing directional data is also provided, and potential future developments discussed. Keywords: Classification; Clustering; Dimension reduction; Distributional
    [Show full text]
  • A General Approach for Obtaining Wrapped Circular Distributions Via Mixtures
    UC Santa Barbara UC Santa Barbara Previously Published Works Title A General Approach for obtaining wrapped circular distributions via mixtures Permalink https://escholarship.org/uc/item/5r7521z5 Journal Sankhya, 79 Author Jammalamadaka, Sreenivasa Rao Publication Date 2017 Peer reviewed eScholarship.org Powered by the California Digital Library University of California 1 23 Your article is protected by copyright and all rights are held exclusively by Indian Statistical Institute. This e-offprint is for personal use only and shall not be self- archived in electronic repositories. If you wish to self-archive your article, please use the accepted manuscript version for posting on your own website. You may further deposit the accepted manuscript version in any repository, provided it is only made publicly available 12 months after official publication or later and provided acknowledgement is given to the original source of publication and a link is inserted to the published article on Springer's website. The link must be accompanied by the following text: "The final publication is available at link.springer.com”. 1 23 Author's personal copy Sankhy¯a:TheIndianJournalofStatistics 2017, Volume 79-A, Part 1, pp. 133-157 c 2017, Indian Statistical Institute ! AGeneralApproachforObtainingWrappedCircular Distributions via Mixtures S. Rao Jammalamadaka University of California, Santa Barbara, USA Tomasz J. Kozubowski University of Nevada, Reno, USA Abstract We show that the operations of mixing and wrapping linear distributions around a unit circle commute, and can produce a wide variety of circular models. In particular, we show that many wrapped circular models studied in the literature can be obtained as scale mixtures of just the wrapped Gaussian and the wrapped exponential distributions, and inherit many properties from these two basic models.
    [Show full text]
  • Package 'Directional'
    Package ‘Directional’ May 26, 2021 Type Package Title A Collection of R Functions for Directional Data Analysis Version 5.0 URL Date 2021-05-26 Author Michail Tsagris, Giorgos Athineou, Anamul Sajib, Eli Amson, Micah J. Waldstein Maintainer Michail Tsagris <[email protected]> Description A collection of functions for directional data (including massive data, with millions of ob- servations) analysis. Hypothesis testing, discriminant and regression analysis, MLE of distribu- tions and more are included. The standard textbook for such data is the ``Directional Statis- tics'' by Mardia, K. V. and Jupp, P. E. (2000). Other references include a) Phillip J. Paine, Si- mon P. Preston Michail Tsagris and Andrew T. A. Wood (2018). An elliptically symmetric angu- lar Gaussian distribution. Statistics and Computing 28(3): 689-697. <doi:10.1007/s11222-017- 9756-4>. b) Tsagris M. and Alenazi A. (2019). Comparison of discriminant analysis meth- ods on the sphere. Communications in Statistics: Case Studies, Data Analysis and Applica- tions 5(4):467--491. <doi:10.1080/23737484.2019.1684854>. c) P. J. Paine, S. P. Pre- ston, M. Tsagris and Andrew T. A. Wood (2020). Spherical regression models with general co- variates and anisotropic errors. Statistics and Computing 30(1): 153--165. <doi:10.1007/s11222- 019-09872-2>. License GPL-2 Imports bigstatsr, parallel, doParallel, foreach, RANN, Rfast, Rfast2, rgl RoxygenNote 6.1.1 NeedsCompilation no Repository CRAN Date/Publication 2021-05-26 15:20:02 UTC R topics documented: Directional-package . .4 A test for testing the equality of the concentration parameters for ciruclar data . .5 1 2 R topics documented: Angular central Gaussian random values simulation .
    [Show full text]
  • Detecting the Direction of a Signal on High-Dimensional Spheres: Non-Null
    Noname manuscript No. (will be inserted by the editor) Detecting the direction of a signal on high-dimensional spheres Non-null and Le Cam optimality results Davy Paindaveine · Thomas Verdebout Received: date / Accepted: date Abstract We consider one of the most important problems in directional statistics, namely the problem of testing the null hypothesis that the spike direction θ of a Fisher{von Mises{Langevin distribution on the p-dimensional unit hypersphere is equal to a given direction θ0. After a reduction through invariance arguments, we derive local asymptotic normality (LAN) results in a general high-dimensional framework where the dimension pn goes to infinity at an arbitrary rate with the sample size n, and where the concentration κn behaves in a completely free way with n, which offers a spectrum of problems ranging from arbitrarily easy to arbitrarily challenging ones. We identify vari- ous asymptotic regimes, depending on the convergence/divergence properties of (κn), that yield different contiguity rates and different limiting experiments. In each regime, we derive Le Cam optimal tests under specified κn and we com- pute, from the Le Cam third lemma, asymptotic powers of the classical Watson test under contiguous alternatives. We further establish LAN results with re- spect to both spike direction and concentration, which allows us to discuss optimality also under unspecified κn. To investigate the non-null behavior of the Watson test outside the parametric framework above, we derive its local Research is supported by the Program of Concerted Research Actions (ARC) of the Univer- sit´elibre de Bruxelles, by a research fellowship from the Francqui Foundation, and by the Cr´editde Recherche J.0134.18 of the FNRS (Fonds National pour la Recherche Scientifique), Communaut´eFran¸caisede Belgique.
    [Show full text]
  • A General Setting for Symmetric Distributions and Their Relationship to General Distributions
    Accepted Manuscript A general setting for symmetric distributions and their relationship to general distributions P.E. Jupp, G. Regoli, A. Azzalini PII: S0047-259X(16)00033-6 DOI: http://dx.doi.org/10.1016/j.jmva.2016.02.011 Reference: YJMVA 4090 To appear in: Journal of Multivariate Analysis Received date: 30 May 2015 Please cite this article as: P.E. Jupp, G. Regoli, A. Azzalini, A general setting for symmetric distributions and their relationship to general distributions, Journal of Multivariate Analysis (2016), http://dx.doi.org/10.1016/j.jmva.2016.02.011 This is a PDF file of an unedited manuscript that has been accepted for publication. Asa service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain. *Manuscript Click here to download Manuscript: asymmetryR3_120216(red).pdf Click here to view linked References A general setting for symmetric distributions and their relationship to general distributions a, b c P.E. Jupp ∗, G. Regoli , A. Azzalini aSchool of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK bDipartimento di Matematica e Informatica, Universit`adi Perugia, 06123 Perugia, Italy cDipartimento di Scienze Statistiche, Universit`adi Padova, 35121 Padova, Italy Abstract A standard method of obtaining non-symmetrical distributions is that of modulating symmetrical distributions by multiplying the densities by a per- turbation factor.
    [Show full text]
  • Projected Multivariate Linear Models for Directional Data
    PROJECTED MULTIVARIATE LINEAR MODELS FOR DIRECTIONAL DATA By PAVLINA RUMCHEVA A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY UNIVERSITY OF FLORIDA 2005 Copyright 2005 by Pavlina Rumcheva To my mother and father, Ludmila and Ignat ACKNOWLEDGMENTS I would like to thank Dr. Brett Presnell for giving me the chance to work with him on this very interesting topic. His guidance and suggestions helped me a lot in my research. I also wish to thank him for being my graduate advisor for all the five years at the University of Florida. I would also like to thank Ramon Littell, Wendy London, Alex Trindade, and Michael Perfit for serving on my committee and taking the time to read my dissertation. Particularly, I would like to thank Dr. Littell for his helpful suggestions related to this topic, and also Wendy, who has been my supervisor at the Children’s Oncology Group for the last three years, for her willingness to answer questions, encouragement, and understanding. I thank Dobrin for all his support throughout my studies. His love and care have been an invaluable part of my life. I would like to thank my parents, Ludmila and Ignat, for stimulating my desire to study and helping me find my own path in life. Finally, I thank my little sister, Irina, for her love and belief in me. IV TABLE OF CONTENTS page ACKNOWLEDGMENTS iv LIST OF TABLES vii LIST OF FIGURES ix ABSTRACT xiii CHAPTER 1 INTRODUCTION 1 2 PROJECTED NORMAL DISTRIBUTION 6 2.1 Definition 6 2.2 The Mean Resultant Length of the Projected Normal Distribution 7 2.3 Comparison with the Fisher Distribution 18 2.4 Conditional Distribution of the Radial Part Given the Direction .
    [Show full text]
  • Directional Statistics: Introduction
    Directional Statistics: Introduction Directional Statistics: Introduction By Riccardo Gattoa and S. Rao Jammalamadakab Keywords: Directional distributions, goodness-of-fit tests, nonparametric inference, robust estimators, rotational invariance, spacings, spacing-frequencies, two-sample tests, von Mises–Fisher distribution Abstract: In many of the natural and physical sciences, measurements are directions, either in two or three dimensions. The analysis of directional data relies on specific statistical models and procedures, which differ from the usual models and methodologies of Cartesian data. This article briefly introduces statistical models and inference for this type of data. The basic von Mises–Fisher distribution is introduced and nonparametric methods such as goodness-of-fit tests are presented. Further references are given for exploring related topics. 1 Introduction This article explores the novel area of directional statistics. In many diverse scientific fields, measurements are directions. For instance, a biologist may be measuring the direction of flight of a bird or the orientation of an animal, whereas a geologist may be interested in the direction of the Earth’s magnetic pole. Such directions may be in two dimensions as in the first two examples or in three dimensions like the last one. A set of such observations on directions is referred to as directional data (see Directional Data Analysis). Langevin[1] and Lévy[2] are two pioneering contributions in this area. One of the first statistical analyses of directional data is Fisher[3]. A two-dimensional direction is a point in ℝ2 without magnitude, for example, a unit vector. It can also be represented as a point on the circumference of the unit circle centered at the origin, denoted S1,oras an angle measured with respect to some suitably chosen “zero direction,” that is, starting point, and “sense of rotation,” that is, whether clockwise or counterclockwise is the positive direction.
    [Show full text]
  • Applied Statistics Using SPSS, STATISTICA, MATLAB and R Joaquim P
    Applied Statistics Using SPSS, STATISTICA, MATLAB and R Joaquim P. Marques de Sá Applied Statistics Using SPSS, STATISTICA, MATLAB and R With 195 Figures and a CD 123 E d itors Prof. Dr. Joaquim P. Marques de Sá Universidade do Porto Fac. Engenharia Rua Dr. Roberto Frias s/n 4200-465 Porto Portugal e-mail: [email protected] Library of Congress Control Number: 2007926024 ISBN 978-3-540-71971-7 Springer Berlin Heidelberg New York This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilm or in any other way, and storage in data banks. Duplication of this publication or parts thereof is permitted only under the provisions of the German Copyright Law of September 9, 1965, in its current version, and permission for use must always be obtained from Springer. Violations are liable for prosecution under the German Copyright Law. Springer is a part of Springer Science+Business Media springer.com © Springer-Verlag Berlin Heidelberg 2007 The use of general descriptive names, registered names, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant pro- tective laws and regulations and therefore free for general use. Typesetting: by the editors Production: Integra Software Services Pvt. Ltd., India Cover design: WMX design, Heidelberg Printed on acid-free paper SPIN: 11908944 42/3100/Integra 5 4 3 2 1 0 To Wiesje and Carlos.
    [Show full text]
  • The Multivariate Generalised Von Mises Distribution: Inference and Applications
    Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17) The Multivariate Generalised von Mises Distribution: Inference and Applications Alexandre K. W. Navarro Jes Frellsen Richard E. Turner Department of Engineering Department of Engineering Department of Engineering University of Cambridge University of Cambridge University of Cambridge Cambridge, UK Cambridge, UK Cambridge, UK [email protected] [email protected] [email protected] Abstract Such an approach would, however, ignore the topology of the space e.g. that φ =0and φ =2π are equivalent. Alter- Circular variables arise in a multitude of data-modelling con- natively, the circular variable can be represented as a unit texts ranging from robotics to the social sciences, but they have vector in R2, x = [cos(φ), sin(φ)], and a standard bivariate been largely overlooked by the machine learning community. This paper partially redresses this imbalance by extending distribution used instead. This partially alleviates the afore- some standard probabilistic modelling tools to the circular mentioned topological problem, but standard distributions domain. First we introduce a new multivariate distribution place probability mass off the unit circle which adversely over circular variables, called the multivariate Generalised affects learning, prediction and analysis. von Mises (mGvM) distribution. This distribution can be con- In order to predict and analyse circular data it is therefore structed by restricting and renormalising a general multivari- key that machine learning practitioners have at their disposal ate Gaussian distribution to the unit hyper-torus. Previously a suite of bespoke modelling, inference and learning meth- proposed multivariate circular distributions are shown to be ods that are specifically designed for circular data (Lebanon special cases of this construction.
    [Show full text]
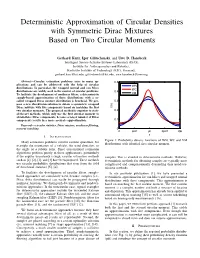
  • Deterministic Approximation of Circular Densities with Symmetric Dirac Mixtures Based on Two Circular Moments
    Deterministic Approximation of Circular Densities with Symmetric Dirac Mixtures Based on Two Circular Moments Gerhard Kurz, Igor Gilitschenski, and Uwe D. Hanebeck Intelligent Sensor-Actuator-Systems Laboratory (ISAS), Institute for Anthropomatics and Robotics, Karlsruhe Institute of Technology (KIT), Germany, [email protected], [email protected], [email protected] Abstract—Circular estimation problems arise in many ap- 0.5 plications and can be addressed with the help of circular WN distributions. In particular, the wrapped normal and von Mises WC distributions are widely used in the context of circular problems. 0.4 To facilitate the development of nonlinear filters, a deterministic VM sample-based approximation of these distributions with a so- called wrapped Dirac mixture distribution is beneficial. We pro- 0.3 pose a new closed-form solution to obtain a symmetric wrapped Dirac mixture with five components based on matching the first f(x) two circular moments. The proposed method is superior to state- 0.2 of-the-art methods, which only use the first circular moment to obtain three Dirac components, because a larger number of Dirac components results in a more accurate approximation. 0.1 Keywords—circular statistics, Dirac mixture, nonlinear filtering, moment matching 0 0 pi/2 pi 3pi/2 2pi x I. INTRODUCTION Figure 1: Probability density functions of WN, WC and VM Many estimation problems involve circular quantities, for distributions with identical first circular moment. example the orientation of a vehicle, the wind direction, or the angle of a robotic joint. Since conventional estimation algorithms perform poorly in these applications, particularly if the angular uncertainty is high, circular estimation methods samples.
    [Show full text]
  • The Power Spherical Distribution
    The Power Spherical distribution Nicola De Cao 1 2 Wilker Aziz 1 Abstract = 10 0.6 p( = /2, = 4) = 100 There is a growing interest in probabilistic models 1k samples = 500 0.5 defined in hyper-spherical spaces, be it to accom- 1 modate observed data or latent structure. The von 0.4 Mises-Fisher (vMF) distribution, often regarded 0.3 0 as the Normal distribution on the hyper-sphere, is 0.2 a standard modeling choice: it is an exponential 1 0.1 1 1 family and thus enjoys important statistical results, 0 0 0.0 for example, known Kullback-Leibler (KL) diver- 0 /2 3 /2 1 1 1 2 gence from other vMF distributions. Sampling (a) On the circle S . (b) On the sphere S . from a vMF distribution, however, requires a re- jection sampling procedure which besides being Figure 1. Example of draws and density function of the Power slow poses difficulties in the context of stochas- Spherical distribution. For the circle (a) we plot both the density tic backpropagation via the reparameterization and histograms for 1k samples. For the sphere (b) we plot draws trick. Moreover, this procedure is numerically from 3 distributions of orthogonal directions (µ) and different unstable for certain vMFs, e.g., those with high concentration parameter κ. concentration and/or in high dimensions. We pro- pose a novel distribution, the Power Spherical distribution, which retains some of the important Bijral et al., 2007), mixed-membership models (Reisinger aspects of the vMF (e.g., support on the hyper- et al., 2010), computer vision (Liu et al., 2017), and natural sphere, symmetry about its mean direction param- language processing (Kumar & Tsvetkov, 2019).
    [Show full text]