Benchmarking Optimization Software with Performance Pro�Les
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University of California, San Diego
UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization . -

Multi-Objective Optimization of Unidirectional Non-Isolated Dc/Dcconverters
MULTI-OBJECTIVE OPTIMIZATION OF UNIDIRECTIONAL NON-ISOLATED DC/DC CONVERTERS by Andrija Stupar A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Edward S. Rogers Department of Electrical and Computer Engineering University of Toronto © Copyright 2017 by Andrija Stupar Abstract Multi-Objective Optimization of Unidirectional Non-Isolated DC/DC Converters Andrija Stupar Doctor of Philosophy Graduate Department of Edward S. Rogers Department of Electrical and Computer Engineering University of Toronto 2017 Engineers have to fulfill multiple requirements and strive towards often competing goals while designing power electronic systems. This can be an analytically complex and computationally intensive task since the relationship between the parameters of a system’s design space is not always obvious. Furthermore, a number of possible solutions to a particular problem may exist. To find an optimal system, many different possible designs must be evaluated. Literature on power electronics optimization focuses on the modeling and design of partic- ular converters, with little thought given to the mathematical formulation of the optimization problem. Therefore, converter optimization has generally been a slow process, with exhaus- tive search, the execution time of which is exponential in the number of design variables, the prevalent approach. In this thesis, geometric programming (GP), a type of convex optimization, the execution time of which is polynomial in the number of design variables, is proposed and demonstrated as an efficient and comprehensive framework for the multi-objective optimization of non-isolated unidirectional DC/DC converters. A GP model of multilevel flying capacitor step-down convert- ers is developed and experimentally verified on a 15-to-3.3 V, 9.9 W discrete prototype, with sets of loss-volume Pareto optimal designs generated in under one minute. -

Julia, My New Friend for Computing and Optimization? Pierre Haessig, Lilian Besson
Julia, my new friend for computing and optimization? Pierre Haessig, Lilian Besson To cite this version: Pierre Haessig, Lilian Besson. Julia, my new friend for computing and optimization?. Master. France. 2018. cel-01830248 HAL Id: cel-01830248 https://hal.archives-ouvertes.fr/cel-01830248 Submitted on 4 Jul 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 1 « Julia, my New frieNd for computiNg aNd optimizatioN? » Intro to the Julia programming language, for MATLAB users Date: 14th of June 2018 Who: Lilian Besson & Pierre Haessig (SCEE & AUT team @ IETR / CentraleSupélec campus Rennes) « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 2 AgeNda for today [30 miN] 1. What is Julia? [5 miN] 2. ComparisoN with MATLAB [5 miN] 3. Two examples of problems solved Julia [5 miN] 4. LoNger ex. oN optimizatioN with JuMP [13miN] 5. LiNks for more iNformatioN ? [2 miN] « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 3 1. What is Julia ? Open-source and free programming language (MIT license) Developed since 2012 (creators: MIT researchers) Growing popularity worldwide, in research, data science, finance etc… Multi-platform: Windows, Mac OS X, GNU/Linux.. -

Click to Edit Master Title Style
Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than -

Specifying “Logical” Conditions in AMPL Optimization Models
Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual -

COSMO: a Conic Operator Splitting Method for Convex Conic Problems
COSMO: A conic operator splitting method for convex conic problems Michael Garstka∗ Mark Cannon∗ Paul Goulart ∗ September 10, 2020 Abstract This paper describes the Conic Operator Splitting Method (COSMO) solver, an operator split- ting algorithm for convex optimisation problems with quadratic objective function and conic constraints. At each step the algorithm alternates between solving a quasi-definite linear sys- tem with a constant coefficient matrix and a projection onto convex sets. The low per-iteration computational cost makes the method particularly efficient for large problems, e.g. semidefi- nite programs that arise in portfolio optimisation, graph theory, and robust control. Moreover, the solver uses chordal decomposition techniques and a new clique merging algorithm to ef- fectively exploit sparsity in large, structured semidefinite programs. A number of benchmarks against other state-of-the-art solvers for a variety of problems show the effectiveness of our approach. Our Julia implementation is open-source, designed to be extended and customised by the user, and is integrated into the Julia optimisation ecosystem. 1 Introduction We consider convex optimisation problems in the form minimize f(x) subject to gi(x) 0; i = 1; : : : ; l (1) h (x)≤ = 0; i = 1; : : : ; k; arXiv:1901.10887v2 [math.OC] 9 Sep 2020 i where we assume that both the objective function f : Rn R and the inequality constraint n ! functions gi : R R are convex, and that the equality constraints hi(x) := ai>x bi are ! − affine. We will denote an optimal solution to this problem (if it exists) as x∗. Convex optimisa- tion problems feature heavily in a wide range of research areas and industries, including problems ∗The authors are with the Department of Engineering Science, University of Oxford, Oxford, OX1 3PJ, UK. -

Introduction to Mosek
Introduction to Mosek Modern Optimization in Energy, 28 June 2018 Micha l Adamaszek www.mosek.com MOSEK package overview • Started in 1999 by Erling Andersen • Convex conic optimization package + MIP • LP, QP, SOCP, SDP, other nonlinear cones • Low-level optimization API • C, Python, Java, .NET, Matlab, R, Julia • Object-oriented API Fusion • C++, Python, Java, .NET • 3rd party • GAMS, AMPL, CVXOPT, CVXPY, YALMIP, PICOS, GPkit • Conda package, .NET Core package • Upcoming v9 1 / 10 Example: 2D Total Variation Someone sends you the left signal but you receive noisy f (right): How to denoise/smoothen out/approximate u? P 2 P 2 minimize ij(ui;j − ui+1;j) + ij(ui;j − ui;j+1) P 2 subject to ij(ui;j − fi;j) ≤ σ: 2 / 10 Conic problems A conic problem in canonical form: min cT x s:t: Ax + b 2 K where K is a product of cones: • linear: K = R≥0 • quadratic: q n 2 2 K = fx 2 R : x1 ≥ x2 + ··· + xng • semidefinite: n×n T K = fX 2 R : X = FF g 3 / 10 Conic problems, cont. • exponential cone: 3 K = fx 2 R : x1 ≥ x2 exp(x3=x2); x2 > 0g • power cone: 3 p−1 p K = fx 2 R : x1 x2 ≥ jx3j ; x1; x2 ≥ 0g; p > 1 q 2 2 2 x1 ≥ x2 + x3; 2x1x2 ≥ x3 x1 ≥ x2 exp(x3=x2) 4 / 10 Conic representability Lots of functions and constraints are representable using these cones. T jxj; kxk1; kxk2; kxk1; kAx + bk2 ≤ c x + d !1=p 1 X xy ≥ z2; x ≥ ; x ≥ yp; t ≥ jx jp = kxk y i p i p 1=n t ≤ xy; t ≤ (x1 ··· xn) ; geometric programming (GP) X 1 t ≤ log x; t ≥ ex; t ≤ −x log x; t ≥ log exi ; t ≥ log 1 + x i 1=n det(X) ; t ≤ λmin(X); t ≥ λmax(X) T T convex (1=2)x Qx + c x + q 5 / 10 Challenge Find a • natural, • practical, • important, • convex optimization problem, which cannot be expressed in conic form. -
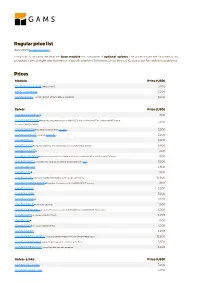
Standard Price List
Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities . -

AJINKYA KADU 503, Hans Freudenthal Building, Budapestlaan 6, 3584 CD Utrecht, the Netherlands
AJINKYA KADU 503, Hans Freudenthal Building, Budapestlaan 6, 3584 CD Utrecht, The Netherlands Curriculum Vitae Last Updated: Oct 15, 2018 Contact Ph.D. Student +31{684{544{914 Information Mathematical Institute [email protected] Utrecht University https://ajinkyakadu125.github.io Education Mathematical Institute, Utrecht University, The Netherlands 2015 - present Ph.D. Candidate, Numerical Analysis and Scientific Computing • Dissertation Topic: Discrete Seismic Tomography • Advisors: Dr. Tristan van Leeuwen, Prof. Wim Mulder, Prof. Joost Batenburg • Interests: Seismic Imaging, Computerized Tomography, Numerical Optimization, Level-Set Method, Total-variation, Convex Analysis, Signal Processing Indian Institute of Technology Bombay, Mumbai, India 2010 - 2015 Bachelor and Master of Technology, Department of Aerospace Engineering • Advisors: Prof. N. Hemachandra, Prof. R. P. Shimpi • GPA: 8.7/10 (Specialization: Operations Research) Work Mitsubishi Electric Research Labs, Cambridge, MA, USA May - Oct, 2018 Experience • Mentors: Dr. Hassan Mansour, Dr. Petros Boufounos • Worked on inverse scattering problem arising in ground penetrating radar. University of British Columbia, Vancouver, Canada Jan - Apr, 2016 • Mentors: Prof. Felix Herrmann, Prof. Eldad Haber • Worked on development of framework for large-scale inverse problems in geophysics. Rediff.com Pvt. Ltd., Mumbai, India May - July, 2014 • Mentor: A. S. Shaja • Worked on the development of data product `Stock Portfolio Match' based on Shiny & R. Honeywell Technology Solutions, Bangalore, India May - July, 2013 • Mentors: Kartavya Mohan Gupta, Hanumantha Rao Desu • Worked on integration bench for General Aviation(GA) to recreate flight test scenarios. Research: Journal • A convex formulation for Discrete Tomography. Publications Ajinkya Kadu, Tristan van Leeuwen, (submitted to) IEEE Transactions on Computational Imaging (arXiv: 1807.09196) • Salt Reconstruction in Full Waveform Inversion with a Parametric Level-Set Method. -

Open Source Tools for Optimization in Python
Open Source Tools for Optimization in Python Ted Ralphs Sage Days Workshop IMA, Minneapolis, MN, 21 August 2017 T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Outline 1 Introduction 2 COIN-OR 3 Modeling Software 4 Python-based Modeling Tools PuLP/DipPy CyLP yaposib Pyomo T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Outline 1 Introduction 2 COIN-OR 3 Modeling Software 4 Python-based Modeling Tools PuLP/DipPy CyLP yaposib Pyomo T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Caveats and Motivation Caveats I have no idea about the background of the audience. The talk may be either too basic or too advanced. Why am I here? I’m not a Sage developer or user (yet!). I’m hoping this will be a chance to get more involved in Sage development. Please ask lots of questions so as to guide me in what to dive into! T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Mathematical Optimization Mathematical optimization provides a formal language for describing and analyzing optimization problems. Elements of the model: Decision variables Constraints Objective Function Parameters and Data The general form of a mathematical optimization problem is: min or max f (x) (1) 8 9 < ≤ = s.t. gi(x) = bi (2) : ≥ ; x 2 X (3) where X ⊆ Rn might be a discrete set. T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Types of Mathematical Optimization Problems The type of a mathematical optimization problem is determined primarily by The form of the objective and the constraints. -

GEKKO Documentation Release 1.0.1
GEKKO Documentation Release 1.0.1 Logan Beal, John Hedengren Aug 31, 2021 Contents 1 Overview 1 2 Installation 3 3 Project Support 5 4 Citing GEKKO 7 5 Contents 9 6 Overview of GEKKO 89 Index 91 i ii CHAPTER 1 Overview GEKKO is a Python package for machine learning and optimization of mixed-integer and differential algebraic equa- tions. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP). Modes of operation include parameter regression, data reconciliation, real-time optimization, dynamic simulation, and nonlinear predictive control. GEKKO is an object-oriented Python library to facilitate local execution of APMonitor. More of the backend details are available at What does GEKKO do? and in the GEKKO Journal Article. Example applications are available to get started with GEKKO. 1 GEKKO Documentation, Release 1.0.1 2 Chapter 1. Overview CHAPTER 2 Installation A pip package is available: pip install gekko Use the —-user option to install if there is a permission error because Python is installed for all users and the account lacks administrative priviledge. The most recent version is 0.2. You can upgrade from the command line with the upgrade flag: pip install--upgrade gekko Another method is to install in a Jupyter notebook with !pip install gekko or with Python code, although this is not the preferred method: try: from pip import main as pipmain except: from pip._internal import main as pipmain pipmain(['install','gekko']) 3 GEKKO Documentation, Release 1.0.1 4 Chapter 2. Installation CHAPTER 3 Project Support There are GEKKO tutorials and documentation in: • GitHub Repository (examples folder) • Dynamic Optimization Course • APMonitor Documentation • GEKKO Documentation • 18 Example Applications with Videos For project specific help, search in the GEKKO topic tags on StackOverflow. -

Insight MFR By
Manufacturers, Publishers and Suppliers by Product Category 11/6/2017 10/100 Hubs & Switches ASCEND COMMUNICATIONS CIS SECURE COMPUTING INC DIGIUM GEAR HEAD 1 TRIPPLITE ASUS Cisco Press D‐LINK SYSTEMS GEFEN 1VISION SOFTWARE ATEN TECHNOLOGY CISCO SYSTEMS DUALCOMM TECHNOLOGY, INC. GEIST 3COM ATLAS SOUND CLEAR CUBE DYCONN GEOVISION INC. 4XEM CORP. ATLONA CLEARSOUNDS DYNEX PRODUCTS GIGAFAST 8E6 TECHNOLOGIES ATTO TECHNOLOGY CNET TECHNOLOGY EATON GIGAMON SYSTEMS LLC AAXEON TECHNOLOGIES LLC. AUDIOCODES, INC. CODE GREEN NETWORKS E‐CORPORATEGIFTS.COM, INC. GLOBAL MARKETING ACCELL AUDIOVOX CODI INC EDGECORE GOLDENRAM ACCELLION AVAYA COMMAND COMMUNICATIONS EDITSHARE LLC GREAT BAY SOFTWARE INC. ACER AMERICA AVENVIEW CORP COMMUNICATION DEVICES INC. EMC GRIFFIN TECHNOLOGY ACTI CORPORATION AVOCENT COMNET ENDACE USA H3C Technology ADAPTEC AVOCENT‐EMERSON COMPELLENT ENGENIUS HALL RESEARCH ADC KENTROX AVTECH CORPORATION COMPREHENSIVE CABLE ENTERASYS NETWORKS HAVIS SHIELD ADC TELECOMMUNICATIONS AXIOM MEMORY COMPU‐CALL, INC EPIPHAN SYSTEMS HAWKING TECHNOLOGY ADDERTECHNOLOGY AXIS COMMUNICATIONS COMPUTER LAB EQUINOX SYSTEMS HERITAGE TRAVELWARE ADD‐ON COMPUTER PERIPHERALS AZIO CORPORATION COMPUTERLINKS ETHERNET DIRECT HEWLETT PACKARD ENTERPRISE ADDON STORE B & B ELECTRONICS COMTROL ETHERWAN HIKVISION DIGITAL TECHNOLOGY CO. LT ADESSO BELDEN CONNECTGEAR EVANS CONSOLES HITACHI ADTRAN BELKIN COMPONENTS CONNECTPRO EVGA.COM HITACHI DATA SYSTEMS ADVANTECH AUTOMATION CORP. BIDUL & CO CONSTANT TECHNOLOGIES INC Exablaze HOO TOO INC AEROHIVE NETWORKS BLACK BOX COOL GEAR EXACQ TECHNOLOGIES INC HP AJA VIDEO SYSTEMS BLACKMAGIC DESIGN USA CP TECHNOLOGIES EXFO INC HP INC ALCATEL BLADE NETWORK TECHNOLOGIES CPS EXTREME NETWORKS HUAWEI ALCATEL LUCENT BLONDER TONGUE LABORATORIES CREATIVE LABS EXTRON HUAWEI SYMANTEC TECHNOLOGIES ALLIED TELESIS BLUE COAT SYSTEMS CRESTRON ELECTRONICS F5 NETWORKS IBM ALLOY COMPUTER PRODUCTS LLC BOSCH SECURITY CTC UNION TECHNOLOGIES CO FELLOWES ICOMTECH INC ALTINEX, INC.