Landing Trajectory Optimization for the Robobee
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University of California, San Diego
UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization . -

An Algorithm Based on Semidefinite Programming for Finding Minimax
Takustr. 7 Zuse Institute Berlin 14195 Berlin Germany BELMIRO P.M. DUARTE,GUILLAUME SAGNOL,WENG KEE WONG An algorithm based on Semidefinite Programming for finding minimax optimal designs ZIB Report 18-01 (December 2017) Zuse Institute Berlin Takustr. 7 14195 Berlin Germany Telephone: +49 30-84185-0 Telefax: +49 30-84185-125 E-mail: [email protected] URL: http://www.zib.de ZIB-Report (Print) ISSN 1438-0064 ZIB-Report (Internet) ISSN 2192-7782 An algorithm based on Semidefinite Programming for finding minimax optimal designs Belmiro P.M. Duarte a,b, Guillaume Sagnolc, Weng Kee Wongd aPolytechnic Institute of Coimbra, ISEC, Department of Chemical and Biological Engineering, Portugal. bCIEPQPF, Department of Chemical Engineering, University of Coimbra, Portugal. cTechnische Universität Berlin, Institut für Mathematik, Germany. dDepartment of Biostatistics, Fielding School of Public Health, UCLA, U.S.A. Abstract An algorithm based on a delayed constraint generation method for solving semi- infinite programs for constructing minimax optimal designs for nonlinear models is proposed. The outer optimization level of the minimax optimization problem is solved using a semidefinite programming based approach that requires the de- sign space be discretized. A nonlinear programming solver is then used to solve the inner program to determine the combination of the parameters that yields the worst-case value of the design criterion. The proposed algorithm is applied to find minimax optimal designs for the logistic model, the flexible 4-parameter Hill homoscedastic model and the general nth order consecutive reaction model, and shows that it (i) produces designs that compare well with minimax D−optimal de- signs obtained from semi-infinite programming method in the literature; (ii) can be applied to semidefinite representable optimality criteria, that include the com- mon A−; E−; G−; I− and D-optimality criteria; (iii) can tackle design problems with arbitrary linear constraints on the weights; and (iv) is fast and relatively easy to use. -

Julia, My New Friend for Computing and Optimization? Pierre Haessig, Lilian Besson
Julia, my new friend for computing and optimization? Pierre Haessig, Lilian Besson To cite this version: Pierre Haessig, Lilian Besson. Julia, my new friend for computing and optimization?. Master. France. 2018. cel-01830248 HAL Id: cel-01830248 https://hal.archives-ouvertes.fr/cel-01830248 Submitted on 4 Jul 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 1 « Julia, my New frieNd for computiNg aNd optimizatioN? » Intro to the Julia programming language, for MATLAB users Date: 14th of June 2018 Who: Lilian Besson & Pierre Haessig (SCEE & AUT team @ IETR / CentraleSupélec campus Rennes) « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 2 AgeNda for today [30 miN] 1. What is Julia? [5 miN] 2. ComparisoN with MATLAB [5 miN] 3. Two examples of problems solved Julia [5 miN] 4. LoNger ex. oN optimizatioN with JuMP [13miN] 5. LiNks for more iNformatioN ? [2 miN] « Julia, my new computing friend? » | 14 June 2018, IETR@Vannes | By: L. Besson & P. Haessig 3 1. What is Julia ? Open-source and free programming language (MIT license) Developed since 2012 (creators: MIT researchers) Growing popularity worldwide, in research, data science, finance etc… Multi-platform: Windows, Mac OS X, GNU/Linux.. -
![[20Pt]Algorithms for Constrained Optimization: [ 5Pt]](https://docslib.b-cdn.net/cover/7585/20pt-algorithms-for-constrained-optimization-5pt-77585.webp)
[20Pt]Algorithms for Constrained Optimization: [ 5Pt]
SOL Optimization 1970s 1980s 1990s 2000s 2010s Summary 2020s Algorithms for Constrained Optimization: The Benefits of General-purpose Software Michael Saunders MS&E and ICME, Stanford University California, USA 3rd AI+IoT Business Conference Shenzhen, China, April 25, 2019 Optimization Software 3rd AI+IoT Business Conference, Shenzhen, April 25, 2019 1/39 SOL Optimization 1970s 1980s 1990s 2000s 2010s Summary 2020s SOL Systems Optimization Laboratory George Dantzig, Stanford University, 1974 Inventor of the Simplex Method Father of linear programming Large-scale optimization: Algorithms, software, applications Optimization Software 3rd AI+IoT Business Conference, Shenzhen, April 25, 2019 2/39 SOL Optimization 1970s 1980s 1990s 2000s 2010s Summary 2020s SOL history 1974 Dantzig and Cottle start SOL 1974{78 John Tomlin, LP/MIP expert 1974{2005 Alan Manne, nonlinear economic models 1975{76 MS, MINOS first version 1979{87 Philip Gill, Walter Murray, MS, Margaret Wright (Gang of 4!) 1989{ Gerd Infanger, stochastic optimization 1979{ Walter Murray, MS, many students 2002{ Yinyu Ye, optimization algorithms, especially interior methods This week! UC Berkeley opened George B. Dantzig Auditorium Optimization Software 3rd AI+IoT Business Conference, Shenzhen, April 25, 2019 3/39 SOL Optimization 1970s 1980s 1990s 2000s 2010s Summary 2020s Optimization problems Minimize an objective function subject to constraints: 0 x 1 min '(x) st ` ≤ @ Ax A ≤ u c(x) x variables 0 1 A matrix c1(x) B . C c(x) nonlinear functions @ . A c (x) `; u bounds m Optimization -

Numericaloptimization
Numerical Optimization Alberto Bemporad http://cse.lab.imtlucca.it/~bemporad/teaching/numopt Academic year 2020-2021 Course objectives Solve complex decision problems by using numerical optimization Application domains: • Finance, management science, economics (portfolio optimization, business analytics, investment plans, resource allocation, logistics, ...) • Engineering (engineering design, process optimization, embedded control, ...) • Artificial intelligence (machine learning, data science, autonomous driving, ...) • Myriads of other applications (transportation, smart grids, water networks, sports scheduling, health-care, oil & gas, space, ...) ©2021 A. Bemporad - Numerical Optimization 2/102 Course objectives What this course is about: • How to formulate a decision problem as a numerical optimization problem? (modeling) • Which numerical algorithm is most appropriate to solve the problem? (algorithms) • What’s the theory behind the algorithm? (theory) ©2021 A. Bemporad - Numerical Optimization 3/102 Course contents • Optimization modeling – Linear models – Convex models • Optimization theory – Optimality conditions, sensitivity analysis – Duality • Optimization algorithms – Basics of numerical linear algebra – Convex programming – Nonlinear programming ©2021 A. Bemporad - Numerical Optimization 4/102 References i ©2021 A. Bemporad - Numerical Optimization 5/102 Other references • Stephen Boyd’s “Convex Optimization” courses at Stanford: http://ee364a.stanford.edu http://ee364b.stanford.edu • Lieven Vandenberghe’s courses at UCLA: http://www.seas.ucla.edu/~vandenbe/ • For more tutorials/books see http://plato.asu.edu/sub/tutorials.html ©2021 A. Bemporad - Numerical Optimization 6/102 Optimization modeling What is optimization? • Optimization = assign values to a set of decision variables so to optimize a certain objective function • Example: Which is the best velocity to minimize fuel consumption ? fuel [ℓ/km] velocity [km/h] 0 30 60 90 120 160 ©2021 A. -

Click to Edit Master Title Style
Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than -

Specifying “Logical” Conditions in AMPL Optimization Models
Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual -
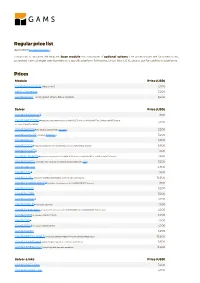
Standard Price List
Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities . -

Open Source Tools for Optimization in Python
Open Source Tools for Optimization in Python Ted Ralphs Sage Days Workshop IMA, Minneapolis, MN, 21 August 2017 T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Outline 1 Introduction 2 COIN-OR 3 Modeling Software 4 Python-based Modeling Tools PuLP/DipPy CyLP yaposib Pyomo T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Outline 1 Introduction 2 COIN-OR 3 Modeling Software 4 Python-based Modeling Tools PuLP/DipPy CyLP yaposib Pyomo T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Caveats and Motivation Caveats I have no idea about the background of the audience. The talk may be either too basic or too advanced. Why am I here? I’m not a Sage developer or user (yet!). I’m hoping this will be a chance to get more involved in Sage development. Please ask lots of questions so as to guide me in what to dive into! T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Mathematical Optimization Mathematical optimization provides a formal language for describing and analyzing optimization problems. Elements of the model: Decision variables Constraints Objective Function Parameters and Data The general form of a mathematical optimization problem is: min or max f (x) (1) 8 9 < ≤ = s.t. gi(x) = bi (2) : ≥ ; x 2 X (3) where X ⊆ Rn might be a discrete set. T.K. Ralphs (Lehigh University) Open Source Optimization August 21, 2017 Types of Mathematical Optimization Problems The type of a mathematical optimization problem is determined primarily by The form of the objective and the constraints. -

GEKKO Documentation Release 1.0.1
GEKKO Documentation Release 1.0.1 Logan Beal, John Hedengren Aug 31, 2021 Contents 1 Overview 1 2 Installation 3 3 Project Support 5 4 Citing GEKKO 7 5 Contents 9 6 Overview of GEKKO 89 Index 91 i ii CHAPTER 1 Overview GEKKO is a Python package for machine learning and optimization of mixed-integer and differential algebraic equa- tions. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP). Modes of operation include parameter regression, data reconciliation, real-time optimization, dynamic simulation, and nonlinear predictive control. GEKKO is an object-oriented Python library to facilitate local execution of APMonitor. More of the backend details are available at What does GEKKO do? and in the GEKKO Journal Article. Example applications are available to get started with GEKKO. 1 GEKKO Documentation, Release 1.0.1 2 Chapter 1. Overview CHAPTER 2 Installation A pip package is available: pip install gekko Use the —-user option to install if there is a permission error because Python is installed for all users and the account lacks administrative priviledge. The most recent version is 0.2. You can upgrade from the command line with the upgrade flag: pip install--upgrade gekko Another method is to install in a Jupyter notebook with !pip install gekko or with Python code, although this is not the preferred method: try: from pip import main as pipmain except: from pip._internal import main as pipmain pipmain(['install','gekko']) 3 GEKKO Documentation, Release 1.0.1 4 Chapter 2. Installation CHAPTER 3 Project Support There are GEKKO tutorials and documentation in: • GitHub Repository (examples folder) • Dynamic Optimization Course • APMonitor Documentation • GEKKO Documentation • 18 Example Applications with Videos For project specific help, search in the GEKKO topic tags on StackOverflow. -

Largest Small N-Polygons: Numerical Results and Conjectured Optima
Largest Small n-Polygons: Numerical Results and Conjectured Optima János D. Pintér Department of Industrial and Systems Engineering Lehigh University, Bethlehem, PA, USA [email protected] Abstract LSP(n), the largest small polygon with n vertices, is defined as the polygon of unit diameter that has maximal area A(n). Finding the configuration LSP(n) and the corresponding A(n) for even values n 6 is a long-standing challenge that leads to an interesting class of nonlinear optimization problems. We present numerical solution estimates for all even values 6 n 80, using the AMPL model development environment with the LGO nonlinear solver engine option. Our results compare favorably to the results obtained by other researchers who solved the problem using exact approaches (for 6 n 16), or general purpose numerical optimization software (for selected values from the range 6 n 100) using various local nonlinear solvers. Based on the results obtained, we also provide a regression model based estimate of the optimal area sequence {A(n)} for n 6. Key words Largest Small Polygons Mathematical Model Analytical and Numerical Solution Approaches AMPL Modeling Environment LGO Solver Suite For Nonlinear Optimization AMPL-LGO Numerical Results Comparison to Earlier Results Regression Model Based Optimum Estimates 1 Introduction The diameter of a (convex planar) polygon is defined as the maximal distance among the distances measured between all vertex pairs. In other words, the diameter of the polygon is the length of its longest diagonal. The largest small polygon with n vertices is the polygon of unit diameter that has maximal area. For any given integer n 3, we will refer to this polygon as LSP(n) with area A(n). -

Users Guide for Snadiopt: a Package Adding Automatic Differentiation to Snopt∗
USERS GUIDE FOR SNADIOPT: A PACKAGE ADDING AUTOMATIC DIFFERENTIATION TO SNOPT∗ E. Michael GERTZ Mathematics and Computer Science Division Argonne National Laboratory Argonne, Illinois 60439 Philip E. GILL and Julia MUETHERIG Department of Mathematics University of California, San Diego La Jolla, California 92093-0112 January 2001 Abstract SnadiOpt is a package that supports the use of the automatic differentiation package ADIFOR with the optimization package Snopt. Snopt is a general-purpose system for solving optimization problems with many variables and constraints. It minimizes a linear or nonlinear function subject to bounds on the variables and sparse linear or nonlinear constraints. It is suitable for large-scale linear and quadratic programming and for linearly constrained optimization, as well as for general nonlinear programs. The method used by Snopt requires the first derivatives of the objective and con- straint functions to be available. The SnadiOpt package allows users to avoid the time- consuming and error-prone process of evaluating and coding these derivatives. Given Fortran code for evaluating only the values of the objective and constraints, SnadiOpt automatically generates the code for evaluating the derivatives and builds the relevant Snopt input files and sparse data structures. Keywords: Large-scale nonlinear programming, constrained optimization, SQP methods, automatic differentiation, Fortran software. [email protected] [email protected] [email protected] http://www.mcs.anl.gov/ gertz/ http://www.scicomp.ucsd.edu/ peg/ http://www.scicomp.ucsd.edu/ julia/ ∼ ∼ ∼ ∗Partially supported by National Science Foundation grant CCR-95-27151. Contents 1. Introduction 3 1.1 Problem Types . 3 1.2 Why Automatic Differentiation? . 3 1.3 ADIFOR ......................................