DOCSLIB.ORG

Hadron Spectroscopy in the Diquark Model

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hadron Spectroscopy in the Diquark Model Hadron Spectroscopy in the Diquark Model Jacopo Ferretti University of Jyväskylä Diquark Correlations in Hadron Physics: Origin, Impact and Evidence September 23-27 2019, ECT*, Trento, Italy Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 1 / 38 Summary Quark Model (QM) formalism Exotic hadrons and their interpretations Fully-heavy and heavy-light tetraquarks in the diquark model The problem of baryon missing resonances Strange and nonstrange baryons in the diquark model Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 2 / 38 Constituent Quark Models Complicated quark-gluon dynamics of QCD 1. Effective degree of freedom of Constituent Quark is introduced: same quantum numbers as valence quarks mass ≈ 1=3 mass of the proton 3. Baryons ! bound states of 3 constituent quarks 4. Mesons ! bound states of a constituent quark-antiquark pair 5. Constituent quark dynamics ! phenomenological (QCD-inspired) interaction Phenomenological models q X 2 2 X αs H = p + m + − + βrij + V (Si ; Sj ; Lij ; rij ) i i r i i<j ij Coulomb-like + linear confining potentials + spin forces Several versions: Relativized Quark Model for baryons and mesons (Capstick and Isgur, Godfrey and Isgur); U(7) Model (Bijker, Iachello and Leviatan); Graz Model (Glozman and Riska); Hypercentral QM (Giannini and Santopinto), ... Reproduce reasonably well many hadron observables: baryon magnetic moments, lower part of baryon and meson spectrum, hadron strong decays, nucleon e.m. form factors ... Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 3 / 38 Relativized Quark Model for Baryons/Mesons S. Godfrey and N. Isgur, Phys. Rev. D 32, 189 (1985) S. Capstick and N. Isgur, Phys. Rev. D 34, 2809 (1986) Relativized QM Hamiltonian q X 2 2 X H = pi + mi + Vconf (rij ) + Vhyp(rij ) + Vso(rij ) i i<j Confining potential 3 3 αs(rij ) Vconf (rij )= − c + βrij − Fi · Fj 4 4 rij Hyperfine interaction αs(rij ) 8π 3 1 3 Si ·rij Sj ·rij Vhyp(rij )= − m m 3 Si · Sj δ (rij ) + 3 r 2 − Si · Sj Fi · Fj i j rij Spin-orbit interaction αs(rij ) 1 1 Si Sj Vso(rij )= − 3 m + m m + m · LFi · Fj rij i j i j Relativistic effects Inserted in the Hamiltonian by means of phenomenological parameterization Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 4 / 38 Charmonium spectrum in the relativized QM S. Godfrey and N. Isgur, Phys. Rev. D 32, 189 (1985) Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 5 / 38 Exotic Hadrons: Possible Interpretations See e.g. Y. R. Liu et al., Prog. Part. Nucl. Phys. 107, 237 (2019) X (3872) [now χc1(3872)]. Discovered by Belle in 2003 in B± ! K ±X (X ! J= π+π−). First observed exotic state. Its properties are not completely compatible with those of a cc¯ state Exotics: Meson and baryon states whose properties and/or quantum numbers cannot be described by considering qq¯ or qqq degrees of freedom only Multiquark states: 1. baryons made up of more than 3 valence quarks qqqqq¯ ! pentaquarks qqqqqq ! exa-quarks or dibaryons 2. mesons made up of more than a qq¯ pair qqq¯q¯ ! tetraquarks Hybrid mesons/baryons: hadrons made up of qqq or qq¯ valence quarks plus gluonic degrees of freedom Glueballs: particles consisting of gluonic degrees of freedom only, without valence quarks Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 6 / 38 Tetraquarks Tetraquarks: bound states of four valence quarks/antiquarks (qqq¯q¯) R.L. Jaffe, Phys. Rev. D 15, 267 & 281 (1977) Combine 4 quarks in terms of qq/q¯q¯ or qq¯ substructures: 1. Compact Tetraquark model: [qq]¯ [¯qq¯]3 3c c 1c 2. Meson-meson molecular mode: [[qq¯] [qq¯] ] 1c 1c 1c 3. Hadro-charmonium model: [qq¯] [QQ¯] 1c 1c 1c q q q q charmonium diquark q c c q q q q light meson q antidiquark compact tetraquark molecule hadro-charmonium Possible mixing between qq¯ and qqq¯ q¯ components Unquenched Quark Model (UQM) Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 7 / 38 Exotic Meson Candidates. Hidden-charm sector PC State J Mexp (MeV) Γ (MeV) Observing Process Experiment X (3872) 1++ 3871:69 ± 0:17 < 1:7 B± ! K ±π+π−J= Belle +− + − + − Zc (3900) 1 3886:6 ± 2:4 28:1 ± 2:6 e e ! π π J= BESIII −− + − + − Y (4008) 1 4008 ± 40 226 ± 44 e e ! γISRπ π J= Belle ± +− + − + − Zc (4020) 1 4024:1 ± 1:9 13 ± 5 e e ! π π hc BESIII ++ +8 X (4140) 1 4146:8 ± 2:5 19−7 γγ ! φJ= CDF ± − +45 +108 0 + − Zc (4240) 0 4239 ± 18−10 220 ± 47−74 B ! K π (2S) LHCb −− + − + − Y (4260) 1 4230 ± 8 55 ± 19 e e ! γISRπ π J= BaBar ++ +19 +14 + + X (4274) 1 4273−9 56−16 B ! J= φK CDF, LHCb −− + − + − Y (4360) 1 4341 ± 8 102 ± 9 e e ! γISRπ π (2S) Belle ± + +15 ± Zc (4430) 1 4478−18 181 ± 31 B ! Kπ (2S) Belle ++ +16 + + X (4500) 0 4506−19 92 ± 29 B ! J= φK LHCb −− +8 +40 + − + − Y (4630) 1 4634−7 92−24 e e ! Λc Λc Belle −− + − + − Y (4660) 1 4643 ± 9 72 ± 11 e e ! γISRπ π (2S) Belle ++ +17 + + X (4700) 0 4704−26 120 ± 50 B ! J= φK LHCb Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 8 / 38 Exotic Mesons. The well-known case of the X (3872) X (3872): JPC = 1++ quantum numbers, narrow width (< 1:2 MeV) Mass Problem: Experimental mass: 3871:69 ± 0:17 MeV [PDG] Incompatible with QM predictions. For example, Relativized QM ! 3.95 GeV X(3872) very close to D0D¯∗0 threshold ) Importance of threshold effects? Peculiar decay modes: Main decay modes are into D0D¯0π0 (Br > 0.4) and D0D¯∗0 (Br > 0.3) J= ρ (isospin violating, Br > 0.032) and J= ! (Br > 0.023) decay modes Decay properties not compatible with those of a cc¯ state Several interpretations: DD¯∗ meson-meson molecule Compact tetraquark (diquark-antidiquark) state cc¯ core + meson-meson pair loops (Unquenched Quark Model interpretation) Hadro-charmonium Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 9 / 38 Meson-meson molecular model See e.g. N. A. Törnqvist, Z. Phys. C 61, 525 (1994) Meson-meson molecules: bound states of two mesons Binding energy is relatively small Emergence of molecular states only close to meson-meson thresholds Binding: one-meson exchange forces and/or contact interactions One-pion-exchange (OPE) potential 2 g (σ1·q)(σ2·q) Vπ(q) = − 2 (τ1 · τ2) 2 2 fπ q +mπ σi and τi (i = 1; 2) ! spin and isospin matrices acting on light quarks i fπ ≈ 132 MeV ! pion decay constant mπ ! pion mass g ! dimensionless coupling constant Molecule wave function Obtained by combining the wave functions of the two meson Consider also relative orbital angular momentum between two mesons Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 10 / 38 Hadro-charmonium (hadro-quarkonium) model S. Dubynskiy and M. B. Voloshin, Phys. Lett. B 666, 344 (2008) J. Ferretti, Phys. Lett. B 782, 702 (2018) Heavy QQ¯ state embodied in a light qq¯ one (Q = c or b; q = u; d or s) Binding provided by multiple gluon-exchange forces QCD analog of van der Waals-type interactions Parametrization of the heavy quarkonium-light meson interaction: ( 2πα M − QQ¯ M for r < R 3R3 M Vhq(r) = M 0 for r > RM RM = light meson radius, MM = light meson mass αQQ¯ = quarkonium diagonal chromo-electric polarizability Hamiltonian: Hhq = MQQ¯ + MM + Vhq(r) + Thq k2 Thq = 2µ , k = relative momentum, µ = reduced mass of the system Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 11 / 38 Unquenched quark model (UQM) K. Heikkila, S. Ono and N. A. Törnqvist, Phys. Rev. D 29, 110 (1984) J. Ferretti, G. Galatà and E. Santopinto, Phys. Rev. C 88, 015207 (2013) Bare meson jAi develops a meson-meson continuum component jBCi " Z # X hBCkj Hqq¯ jAi j Ai = NA jAi + dk jBCki MA − EB − EC BC ¯ ¯ jAi = QQ ; jBCi = qQ − Qq¯ ; Hqq¯ = pair-creation operator UQM Hamiltonian HUQM = HA + HBC + Hqq¯ HA(HB;C) ! QQ¯ (qQ¯) bare meson Hamiltonian of A (B and C) ! REL QM Hqq¯ ! couples A to BC meson-meson components by creating a light qq¯ pair Physical Mass of a meson A: MA = EA +Σ( MA)= bare mass + self-energy correction Self-energy corrections Z 1 2 X jhBCkj Hqq¯ jAij Σ(MA) = dk MA − EB − EC BC 0 Sum over a complete set of intermediate states jBCi Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 12 / 38 Compact tetraquark (diquark-antidiquark) model (I) Compact tetraquarks: diquark-antidiquark bound states 4 body problem ! 2 body one ρ D q3 q4 q3 q4 λ r ≈ r q1 q2 q1 q2 σ D Diquark: Effective bosonic degree of freedom 2 strongly correlated quarks with no internal spatial excitation Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 13 / 38 Compact tetraquark (diquark-antidiquark) model (II) Possible diquark color configurations: color antitriplet (3¯c, attractive interaction) color sextet (6c, repulsive interaction) ) 3¯c is favored Diquark WF: ΨD = ΨspaceΨcolorΨspin−flavor is antisymmetric (Pauli principle) ) Ψspin−flavor is symmetric Diquark spin-flavor wave function: decomposed in terms of S = 0, 3¯f (scalar diquark) S = 1, 6f (axial-vector diquark) OGE calculations ) scalar configuration is energetically favored Jacopo Ferretti (University of Jyväskylä) hadron spectroscopy (diquark model) Sept 23-27 2019, ECT* 14 / 38 Compact tetraquark (diquark-antidiquark) model (III) Different approaches to study tetraquark properties: Potential models Algebraic models QCD calculations Mass inequality relations and so on Diquark models for tetraquarks: Several versions L.
Load more

Recommended publications
  • Arxiv:1912.09659V2 [Hep-Ph] 20 Mar 2020
    2 spontaneous chiral-symmetry breaking, i.e., quark con- responding nonrelativistic quark model assignments are densates, generates a diquark mass term, which behaves given of the spin and orbital angular momentum. differently from the other mass terms. We discuss how we can identify and determine the parameters of such a coupling term of the diquark effective Lagrangian. B. Scalar and pseudo-scalar diquarks in chiral This paper is organized as follows. In Sec. II, we SU(3)R × SU(3)L symmetry introduce diquarks and their local operator representa- tion, and formulate chiral effective theory in the chiral- In this paper, we concentrate on the scalar and pseu- symmetry limit. In Sec. III, explicit chiral-symmetry doscalar diquarks from the viewpoint of chiral symmetry. breaking due to the quark masses is introduced and its More specifically, we consider the first two states, Nos. 1 consequences are discussed. In Sec. IV, a numerical esti- and 2, from Table I, which have spin 0, color 3¯ and flavor mate is given for the parameters of the effective theory. 3.¯ We here see that these two diquarks are chiral part- We use the diquark masses calculated in lattice QCD and ners to each other, i.e., they belong to the same chiral also the experimental values of the singly heavy baryons. representation and therefore they would be degenerate if In Sec. V, a conclusion is given. the chiral symmetry is not broken. To see this, using the chiral projection operators, a PR;L ≡ (1 ± γ5)=2, we define the right quark, qR;i = a II.
    [Show full text]
  • Cooling of Hybrid Neutron Stars and Hypothetical Self-Bound Objects with Superconducting Quark Cores
    A&A 368, 561–568 (2001) Astronomy DOI: 10.1051/0004-6361:20010005 & c ESO 2001 Astrophysics Cooling of hybrid neutron stars and hypothetical self-bound objects with superconducting quark cores D. Blaschke1,2,H.Grigorian1,3, and D. N. Voskresensky4 1 Fachbereich Physik, Universit¨at Rostock, Universit¨atsplatz 1, 18051 Rostock, Germany 2 European Centre for Theoretical Studies ECT∗, Villa Tambosi, Strada delle Tabarelle 286, 38050 Villazzano (Trento), Italy 3 Department of Physics, Yerevan State University, Alex Manoogian Str. 1, 375025 Yerevan, Armenia e-mail: [email protected] 4 Moscow Institute for Physics and Engineering, Kashirskoe shosse 31, 115409 Moscow, Russia Gesellschaft f¨ur Schwerionenforschung GSI, Planckstrasse 1, 64291 Darmstadt, Germany e-mail: [email protected] Received 19 September 2000 / Accepted 12 December 2000 Abstract. We study the consequences of superconducting quark cores (with color-flavor-locked phase as repre- sentative example) for the evolution of temperature profiles and cooling curves in quark-hadron hybrid stars and in hypothetical self-bound objects having no hadron shell (quark core neutron stars). The quark gaps are varied from 0 to ∆q = 50 MeV. For hybrid stars we find time scales of 1 ÷ 5, 5 ÷ 10 and 50 ÷ 100 years for the formation of a quasistationary temperature distribution in the cases ∆q =0,0.1MeVand∼>1 MeV, respectively. These time scales are governed by the heat transport within quark cores for large diquark gaps (∆ ∼> 1 MeV) and within the hadron shell for small diquark gaps (∆ ∼< 0.1 MeV). For quark core neutron stars we find a time scale '300 years for the formation of a quasistationary temperature distribution in the case ∆ ∼> 10 MeV and a very short one for ∆ ∼< 1 MeV.
    [Show full text]
  • Uwthph-81-28 QUARK and DIQUARK FRAGMENTATION INTO
    UWThPh-81-28 QUARK AND DIQUARK FRAGMENTATION INTO «SONS AND BARYONS A. Bartl Institut für Theoretische Physik Universität Wien A-1090 Wien, Austria H. Fraas Physikalisches Institut Universität Würzburg D-8700 Würzburg, Federal Republik of Germany U. Majerotto Institut für Hochenergiephysik Österreichische Akademie der Wissenschaften A-1050 Wien» Austria Abstract Quark and diquark fragmentation into mesons and baryons is treated in a cascade-type model based on six coupled integral equations. An analytic solution including flavour dependence is found. Comparison with experimental data is given. Our results indicate a probability of about 50 percent for the diquark to break up. +) Supported in part by "Fonds zur Förderung der wissenschaftlichen Forschung in Österreich", Project number 4347. 1 I. Introduction It is conmonly accepted that quarks are confined and fragment into jets of hadrons which are observed in high energy reactions. The properties of these jets are usually described in terns of so-called fragmentation functions. In the phenomenological picture which has been developed to understand this process of hadronization (see e.g. ref. 1-3) the frag­ mentation of a highly energetic quark into mesons proceeds by creation of quark-antiquark pairs in the colour field of the original quark and recursive pairing of quarks with antiquarks starting with the original quark. In quark jets also baryons are produced [4] at a rate of 5-10 percent. This can be incorporated into the phenomenological description by assuming that also diquark-antidiquark pairs are created and a quark together with a diquark forms a baryon [5]. What concerns colour the diquark behaves like an antiquark, but since it has a higher effective mass than a quark diquark-antidiquark pairs are produced less frequently.
    [Show full text]
  • Hadronic Superpartners from Superconformal And
    SLAC-PUB-17231 Hadronic Superpartners from Superconformal and Supersymmetric Algebra Marina Nielsen1 Instituto de F´ısica, Universidade de S˜ao Paulo Rua do Mat˜ao, Travessa R187, 05508-900 S˜ao Paulo, S˜ao Paulo, Brazil SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94309, USA Stanley J. Brodsky2 SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94309, USA Abstract Through the embedding of superconformal quantum mechanics into AdS space, it is possible to construct an effective supersymmetric QCD light-front Hamilto- nian for hadrons, which includes a spin-spin interaction between the hadronic con- stituents. A specific breaking of conformal symmetry determines a unique effective quark-confining potential for light hadrons, as well as remarkable connections be- tween the meson, baryon, and tetraquark spectra. The pion is massless in the chiral limit and has no supersymmetric partner. The excitation spectra of rela- tivistic light-quark meson, baryon and tetraquark bound states lie on linear Regge arXiv:1802.09652v1 [hep-ph] 27 Feb 2018 trajectories with identical slopes in the radial and orbital quantum numbers. Al- though conformal symmetry is strongly broken by the heavy quark mass, the basic underlying supersymmetric mechanism, which transforms mesons to baryons (and baryons to tetraquarks) into each other, still holds and gives remarkable connec- tions across the entire spectrum of light, heavy-light and double-heavy hadrons. Here we show that all the observed hadrons can be related through this effective supersymmetric QCD, and that it can be used to identify the structure of the new charmonium states. [email protected] [email protected] This material is based upon work supported by the U.S.
    [Show full text]
  • Supersymmetry in the Quark-Diquark and the Baryon-Meson Systems
    Acta Polytechnica Vol. 51 No. 1/2011 Supersymmetry in the Quark-Diquark and the Baryon-Meson Systems S. Catto, Y. Choun Abstract A superalgebra extracted from the Jordan algebra of the 27 and 27¯ dim. representations of the group E6 is shown to be relevant to the description of the quark-antidiquark system. A bilocal baryon-meson field is constructed from two quark-antiquark fields. In the local approximation the hadron field is shown to exhibit supersymmetry which is then extended to hadronic mother trajectories and inclusion of multiquark states. Solving the spin-free Hamiltonian with light quark masses we develop a new kind of special function theory generalizing all existing mathematical theories of confluent hypergeometric type. The solution produces extra “hidden” quantum numbers relevant for description of supersymmetry and for generating new mass formulas. Keywords: supersymmetry, relativistic quark model. A colored supersymmetry scheme based on SU(3)c × SU(6/1) Algebraic realization of supersymmetry and its experimental consequences based on supergroups of type SU(6/21) and color algebras based on split octonionic units ui (i =0,...,3) was considered in our earlier papers[1,2,3,4,5].Here,weaddtothemthelocalcolorgroupSU(3)c. We could go to a smaller supergroup having SU(6) as a subgroup. With the addition of color, such a supergroup is SU(3)c × SU(6/1). The fun- damental representation of SU(6/1) is 7-dimensional which decomposes into a sextet and a singlet under the spin-flavor group. There is also a 28-dimensional representation of SU(7). Under the SU(6) subgroup it has the decomposition 28 = 21 + 6 + 1 (1) Hence, this supermultiplet can accommodate the bosonic antidiquark and fermionic quark in it, provided we are willing to add another scalar.
    [Show full text]
  • An Overview of Some Recent Theory Developments in Neutron Oscillations
    An overview of some recent theory developments in Neutron oscillations R. N. Mohapatra “Workshop on. Baryon violation by 2 units” ACFI, August 3-6, 2020 Why search for B-violation (B) vThere are many good reasons to think that baryon and lepton number are violated in nature e.g.: (i) Understanding the origin of matter in the universe using Sakharov’s conditions; (ii) Many beyond the standard model theories predict specific kinds of B-violation (B); (iii) Standard model itself breaks B nonperturbatively via sphalerons Two Major classes of B • Proton decay : Δ� = 1 (probes high scale physics and if discovered will strengthen the case for grand unified theory of forces and matter) • Neutron-anti-neutron oscillation: Δ� = 2 (Probes physics in the 1-100 TeV scale range, testable in colliders unlike p-decay P-decay vs N-N-bar osc. • GUTs generically predict canonical p-decay pàe+ π0 ,K+ � ; p life time model dependent. Scales like ~M-4 • N-N-bar predicted in theories with Majorana neutrino when extended to quark lepton unification; nn-bar oscillation time scales like ~M-5 . May also exist in some GUT models at observable levels. NN-bar oscillation directly connected to origin of matter! Provides an additionl handle on testing it ! Canonical Proton decay in GUTs not connected to baryogenesis ! Does not lead to baryon asymmetry! Phenomenology for free and bound neutrons, Key parameter Oscillation time �: Facts: free n: � > 8.7x107 sec.(ILL) Super-K : for bound nà τ > 3.5 × 108 sec. ESS possible improvement by ~30 (very important) Case for free NNbar vs bound NNbar: (i) How far does the sensitivity of bound NNbar go: atmospheric bg? (Barrow’s talk) (ii) To put bounds on LIV and equivalence principle etc.
    [Show full text]
  • Opportunities in Diquark Physics
    Opportunities in Diquark Physics Kenji Fukushima The University of Tokyo JAEA/ASRC Reimei Workshop New exotic hadron matter at J-PARC October 24, 2016 @ Inha U 1 Diquarks — where? Diquarks in Matter □ Phases of QCD and diquarks □ Color superconductivity — theoretical illusion? □ Diquark condensate in nuclear matter Diquarks in Hadrons □ Diquark correlation in baryons □ Phenomenological mass formula and diquarks □ Implication from hadrons to matter October 24, 2016 @ Inha U 2 Phases of QCD Nuclear Superfluid Chemical Potential μB Fukushima-Hatsuda (2010) / Fukushima-Sasaki (2013) October 24, 2016 @ Inha U 3 Phases of QCD Complicated structures with various diquark condensates Nuclear Superfluid Chemical Potential μB Fukushima-Hatsuda (2010) / Fukushima-Sasaki (2013) October 24, 2016 @ Inha U 4 Diquark Condensation Phases In b-equlibrium Many diquarks — many phases Instabilities (Crystallized) All complications by s-quarks Fukushima (2005) October 24, 2016 @ Inha U 5 Caution! Your phase diagram may not be the phase diagram for neutron stars or for heavy-ion collision (HIC) Neutron Stars Electric neutrality condition (n-rich; electron density) b-equilibrium (hyperons to lower the Fermi surface) HIC Electric charge conservation (Q/(p+n) fixed) Zero net strangeness (L, S compensated by K) October 24, 2016 @ Inha U 6 performed at nonzero temperature, and small values of µB without running into problems of principle. At µB = 0, these simulations indicate that there is no true phase transition from Hadronic Matter to a Quark-Gluon Plasma, but rather a very rapid rise in the energy density at a temperature Tc which lines in 160 Particle190 MeV within the systematic Abundances errors. Further, studies using the in HIC ° lattice technique imply that Tc decreases very little as µB increases, at least for moderate values of µB.
    [Show full text]
  • Melting Pattern of Diquark Condensates in Quark Matter
    Melting Pattern of Diquark Condensates in Quark Matter ーGinzburg-Landau approach in Color Superconductivityー Based on hep-ph/0312363 Motoi Tachibana (RIKEN) Kei Iida（RIKEN-BNL） Taeko Matsuura (Univ. Tokyo) Tetsuo Hatsuda (Univ. Tokyo) 1. Introduction T 150MeV Quark-Gluon Plasma Hadron Color Superconductivity μ 400MeV Neutron Star Core? (Conjectured) Phase Diagram of Hot and Dense Quark Matter Color Superconductivity Characterized by diquark condensate <qq> Attractive force via color 3-bar gluon exchange Lots of internal d.o.f such as spin, charge, color & flavor ‡Complicated phase structures depending on T & μ Taking into account for the nonzero strange quark mass and the charge neutralities →Much closer situation for the real systems (Already) lots of phases in color superconductivity Originally 2SC CFL 1997 Then Crystalline Kaon condensed CFL 2000 More recently Gapless 2SC Gapless CFL 2003 Much more recently CFL-η Last week Purpose of this study Investigation of thermal phase transition in color superconducting quark matter with 3 flavors and 3 colors, particularly emphasizing on the interplay between effects of the strange quark mass ( m s ) & electric and color charge neutrality near the transition temperatures. Ginzburg-Landau approach near Tc ＋ † weak coupling analysis Result Single Phase transition Multiple phase transitions (m 0) ms ≠ 0 s = dSC as a new phase † † 2. Ginzburg-Landau a la Iida-Baym PRD63(’01)074018 GL potential (mu,d ,s = 0) r 2 r 2 2 r * r 2 S = a | d a | + b1( | d a | ) + b2 | d a ⋅ d b | Â Â Â i, j,k = u,d,s
    [Show full text]
  • Muon Scattering and Dimuon Production
    Muon Scattering and Dimuon Production Ell Gabathuler, CERN Session Organizer THE EMC MUON SCATTERING EXPERIMENT AT CERN Hans-Erhart Stier University of Freiburg D-7800 Freiburg, Germany European Muon Collaboration: O.C. Allkofer4 , J.J. Aubert6, G. Bassompierre6, K.H. Becks l2 , Y. Bertsch6, C. Bestl , E. Bohm4 , D.R. Botteril19 , F.W. Brasse2, C. Bro116, J. Carr9 , R.W. Clifft9 , J.H. CobbS, G. Coignet6, F. CombleylO, G.R. Court7 , J.M. cres~o6, P. Dalpiazll , P.F. Dalpiazll , W.D. Dau 4 , J.K. Davies8 , Y. Declais6, R.W. Dobinson1 , J. Dreesl2 , A. Edwards, M. Edwards9! J. Favier6, M.I. Ferrero1l , W. Flauger2, E. Gabathuler1, R. Gamet 7, J. Gayler2, C. Gossling2 , P. Gregory, J. Haas 3 , U. Hahn 3 , P. Hayman7 , M. Henckes l2 , J.R. Holt7, H. Jokisch4 , 9 V. Korbel 2 , U. Landgraf 3 , M. Leenen1,L. Massonnet6, W. Mohr 3 , H.E. Montgomery!, K. Hose:r 3 , R.P.Eount8 , P.R.Norton , A.M. Osbornel , P. Payrel , C. Peronill , H. Pessard6, K. Rith1 , M.D. Rousseau9 , E. Schlosser3 , M. Schneegans6 , T. SloanS, M. Sproston9 , H.E. Stier3 , W. Stockhausenl2 , J.M. Thenard6 , J.C. Thompson9 , L. Urban6 , G. von Holteyl, H. Wahlenl , V.A. White l , D. Williams7, W.S.C. Williams8, S.J. WimpennylO. CERN l -DESY(Hamburg)2-Freiburg3- Kiel4- LancasterS-LAPP(Annecy)6- Liverpool7- Oxford8- Rutherford9- Sheffield1Q ­ Turinll and Wuppertall2 • I.) Introduction v = E- E' and its imaginary mass squared Q2: The investigation of the hadronic structure of the nu­ cleon is one of the most interesting questions in high Q2= -4EE'sin2 0/2 energy physics.
    [Show full text]
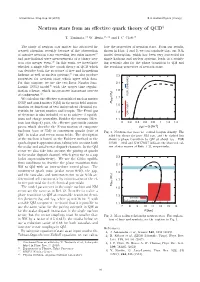
  • Neutron Stars from an Effective Quark Theory of QCD†
    RIKEN Accel. Prog. Rep. 52 (2019) Ⅱ-5. Hadron Physics (Theory) Neutron stars from an effective quark theory of QCD† 1 1, 2 3 T. Tanimoto,∗ W. Bentz,∗ ∗ and I. C. Cloët∗ The study of neutron star matter has attracted in- late the properties of neutron stars. From our results, creased attention recently because of the observation shown in Figs. 1 and 2, we can conclude that our NJL of massive neutron stars exceeding two solar masses1) model description, which has been very successful for and gravitational wave measurements of a binary neu- single hadrons and nuclear systems, leads to a satisfy- tron star merger event.2) In this work, we investigate ing scenario also for the phase transition to QM and whether a single effective quark theory of QCD which the resulting properties of neutron stars. can describe both the structure of free and in-medium hadrons as well as nuclear systems,3) can also produce properties for neutron stars which agree with data. For this purpose, we use the two-flavor Nambu-Jona- Lasinio (NJL) model4) with the proper-time regular- ization scheme, which incorporates important aspects of confinement.3) We calculate the effective potentials of nuclear matter (NM) and quark matter (QM) in the mean field approx- imation as functions of two independent chemical po- tentials for baryon number and isospin. The Fermi gas of electrons is also included so as to achieve β equilib- rium and charge neutrality. Besides the vacuum (Mex- ican hat shaped) part, the effective potentials contain pieces which describe the Fermi motion of composite nucleons (case of NM) or constituent quarks (case of Fig.
    [Show full text]
  • Exotic Diquark Spectroscopy
    Exotic Diquark Spectroscopy JLab R.L. Jaffe November 2003 F. Wilczek hep-ph/0307341 The discovery of the Θ+(1540) this year marks the beginning of a new and rich spectroscopy in QCD. What are the foundations of this physics? Why this channel? What is the underlying dynamics? What implications for QCD? What predictions to test ideas? R Jaffe JLab November, 2003 1 Assumed Properties of the Θ+(1540) 1 It exists ? J = 2 Flat angular distribution Mass 1540 MeV Width 10 MeV ???? How Narrow? Parity Unknown! Very Narrow? + K n quantum numbers: Y Θ+ Y =2 I3 =0 I3 I =0 (no K+p partner) R Jaffe JLab November, 2003 2 First Manifestly Exotic Hadron in 40 Years • What dynamical principles are operating here? • What are the further consequences? • Strong correlation of color, ⇐ THIS TALK flavor, and spin antisymmetric quark pairs into DIQUARKS. Y + _ Θ uudds • Two relatively light, narrow EXOTIC CASCADES await I3 discovery. • -- _ + _ Possible stable? charm and Ξ ssddu Ξ uussd bottom analogues. R Jaffe JLab November, 2003 3 Interpretations of the Θ+ • Chiral Soliton Model (motivated experiments) A narrow K+n resonance generated by chiral dynamics. Chemtob (1984) ; Praszalowicz (1987) Diakonov, Petrov, Polyakov (1997) • Uncorrelated Quark Model Q4Q¯ in the lowest orbital of some mean field: NRQM, bag, . RLJ (1976), Strottman (1978), Wybourne Carlson, Carone, Kwee, & Nazaryan,. • Correlated (Diquark) Description [QQ] correlated in an antisymmetric color, flavor, and spin state. ⇔ Q2Q¯2 mesons, color superconductivity. Jaffe & Wilczek [For a different
    [Show full text]
  • Neutral and Charged Scalar Mesons, Pseudoscalar Mesons, and Diquarks in Magnetic Fields
    PHYSICAL REVIEW D 97, 076008 (2018) Neutral and charged scalar mesons, pseudoscalar mesons, and diquarks in magnetic fields Hao Liu,1,2,3 Xinyang Wang,1 Lang Yu,4 and Mei Huang1,2,5 1Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, People’s Republic of China 2School of Physics Sciences, University of Chinese Academy of Sciences, Beijing 100039, China 3Jinyuan Senior High School, Shanghai 200333, China 4Center of Theoretical Physics and College of Physics, Jilin University, Changchun 130012, People’s Republic of China 5Theoretical Physics Center for Science Facilities, Chinese Academy of Sciences, Beijing 100049, People’s Republic of China (Received 16 January 2018; published 17 April 2018) We investigate both (pseudo)scalar mesons and diquarks in the presence of external magnetic field in the framework of the two-flavored Nambu–Jona-Lasinio (NJL) model, where mesons and diquarks are constructed by infinite sum of quark-loop chains by using random phase approximation. The polarization function of the quark-loop is calculated to the leading order of 1=Nc expansion by taking the quark propagator in the Landau level representation. We systematically investigate the masses behaviors of scalar σ meson, neutral and charged pions as well as the scalar diquarks, with respect to the magnetic field strength at finite temperature and chemical potential. It is shown that the numerical results of both neutral and charged pions are consistent with the lattice QCD simulations. The mass of the charge neutral pion keeps almost a constant under the magnetic field, which is preserved by the remnant symmetry of QCD × QED in the vacuum.
    [Show full text]