A Two-Step Linear Programming Model for Energy-Efficient Timetables in Metro Railway Networks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CRAC Brochure
Shanghai | Oct 13-14, 2014 European Chemicals Agency | EPA US | MOE China | MOE Korea | EPA Taiwan | METI Japan | SAWs-NRCC | Local CIQ China | ICAMA | CtGB, the Nethalands Organizer: REACH24H Consulting Group (a member company of CTI Group) / Supported by ChemLinked Co-organizer: Zhejiang Institute of Standardization (ZIS) Zhejiang WTO/TBT Research & Response Center Technical support: Chinese Industry Association for Antimicrobial Materials & Products (CIAA) With the unprecedented success of last year’s CRAC 2013, REACH24H have set the bar even higher for 2014. We are committed to providing an even better platform for exchange and dissemination of the most important cross boarder regulatory and practical compliance information for enterprises operating in China and Europe, the US and the wider Asian Pacific region. This year's CRAC is to be held at InterContinental Shanghai Puxi on Oct 13-14 (Mon & Tue)2014. Since last year’s conference the industry and regulatory environment has moved forward, legislations have been amended and new regulations implemented in our collective global efforts to ensure a safer and more efficient management of Chemicals throughout the entire supply chain. What hasn’t changed is REACH24H’s commitment to host a meaningful event with an industry focus. CRAC is an event where practical issues facing industry are discussed and presented to policymakers, NGO’s and leading industrial players alike. CRAC is an event where genuine constructive dialogue converts into take-home information which help attendees come to terms with the most important developments in the Sino-global regulatory environment. YOUR GATEWAY TO CHINESE AND GLOBAL REGULATORY AFFAIRS Professional Gathering in China to address concerns raised by regional and international stakeholders in regard to changes in chemical management frameworks and implementation of regulations. -

US Military Shifts Army Basing from Qatar to Jordan
PACIFIC: See Hawaii the way locals wish you would Page 24 EUROPE Smoked beer and GAMES: Mario Golf is medieval history worth teeing up Page 19 make Bamberg NBA PLAYOFFS: Chris Paul memorable Page 21 finally reaches Finals Page 48 stripes.com Volume 80 Edition 55 ©SS 2021 FRIDAY,JULY 2, 2021 $1.00 US military shifts Army basing from Qatar to Jordan BY J.P. LAWRENCE Stars and Stripes The U.S. has closed sprawling bases in Qatar that once stored warehouses full of weaponry and transferred the remaining suppli- es to Jordan, in a move that analy- sts say positions Washington to deal better with Iran and reflects the military’s changing priorities in the region. Military leaders shuttered U.S. Army Camp As Sayliyah-Main last month, along with Camp As Sayliyah-South, and an ammuni- tion supply point named Falcon, an Army statement last week said. Camp As Sayliyah was known among many service members for its Rest and Recuperation Pass Program, which gave some EFFRAIN LOPEZ/U.S. Air Force 200,000 deployed troops a four- An MQ-1 Predator flies over the Southern California Logistics Airport in Victorville, Calif., in 2012. The drone was a catalyst for extraordinary day vacation. The program ran growth and change in the world of unmanned aerial vehicles, but it also raised ethical questions regarding death by remote control. from 2002 to 2011 and offered trav- elers up to two glasses of beer or wine a day, along with golf and beach trips. The camp also served as a for- ward staging area for U.S. -

GR8-1202 Multitasking Battery and Electrical Diagnostic Station
April 2013 167-000497EN-A GR8-1202 Multitasking Battery And Electrical Diagnostic Station INSTRUCTION MANUAL This page intentionally left blank. GR8-1202 Contents Contents Safety Guidelines 5 Chapter 2: Battery Test 17 General Safety Precautions 5 Test Requirements 17 Personal Precautions 5 Additional Test Requirements 18 Preparing To Charge The Battery 6 System Noise Detected 18 Grounding & Power Cord Connections 6 Unstable Battery Detected 18 Charger Location 7 Deep Scan Test 18 DC Connection Precautions 7 Battery Test Results 18 Installing The Battery 7 State of Health 19 Connecting To The Battery 8 State-of-Charge 19 Chapter 1: Introduction & Overview 9 Chapter 3: Diagnostic Charging 20 Safety Reminder 9 Charging Modes 21 Safety Precautions 9 Initial Analysis 21 Assembling the GR8 9 Deep Scan Test 21 Attaching the Control Module 9 Diagnostic Mode 21 Installing the Multitasker Module 10 Aborting a Charge Session 21 Front of GR8 11 Completing a Charge Session 22 Back of GR8 11 Diagnostic Charge Results 22 Control Module Keypad 12 Top-Off Mode 22 Data Entry Methods 13 Menu Icons 13 Chapter 4: System Test 23 Option Buttons 13 Starter Test 23 Scrolling Lists 13 Starter System Test Results 23 Alphanumeric Entry 13 Charging System Test 24 Value Boxes 13 Key-Off Draw 24 Main Menu 13 Charging System Test Results 25 Info Menu 14 Chapter 5: ECM Power Supply 26 DMM Menu 14 Setup Menu 14 Chapter 6: Jump Start 27 Setting User Preferences 15 Help Menu 15 Chapter 7: Manual Charging 28 Multitasking 15 Wireless Multitasking 15 Chapter 8: Info Menu 30 Procedure Example 15 View Test Battery 30 Inspecting the Battery 15 View Test Charger 30 Testing Out-of-Vehicle (Battery Test) 15 View Cable Test 30 Testing In-Vehicle (System Test) 16 View Inventory Test 30 Connecting to the Battery 16 Totals 30 Initial Power-up 16 Transfer 31 Selecting A Language 16 View Wireless 31 Version 31 www.midtronics.com 3 Midtronics Inc. -

Travel Information
Travel Information 20th IEEE/ACIS International Conference on Computer and Information Science (ICIS 2021 Summer) June 23-24, 2021 Shanghai Development Center of Computer Software Technology Shanghai http://acisinternational.org/conferences/icis-2021/ Venue for the Conference Shanghai Development Center of Computer Software Technology (SSC) Full address: Technology Building, No. 1588 Lianhang Rd, Minhang District, 201112, Shanghai, China Host Contact: Ms. Yun Hu [email protected] Tel. 86-021-54325166-3313 Travel Information Taxi service: SSC is around 30 km (about 120 CNY) from Shanghai Hongqiao International Airport (SHA), Hongqiao Railway Station and 40 km (about 150 CNY) from Shanghai Pudong International Airport (PVG). Location of SSC from Shanghai Hongqiao International Airport Location of SSC from Shanghai Pudong International Airport Public Transportation: From Shanghai Hongqiao International Airport: From To Transportation Notes Hongqiao International Laoximeng Station Shanghai Metro Line 10 Airport Terminal 2 Direction: Jilong Road Laoximeng Station Lianhang Road Station Shanghai Metro Line 8 Transfer Direction: Shendu Highway inside the station Lianhang Road Station SSC Walk (about 10 min, 500m) From Hongqiao Railway Station: From To Transportation Notes Hongqiao Railway Laoximeng Station Shanghai Metro Line 10 Station Direction: Jilong Road Laoximeng Station Lianhang Road Station Shanghai Metro Line 8 Transfer Direction: Shendu Highway inside the station Lianhang Road Station SSC Walk (about 10 min, 500m) From Shanghai Pudong International Airport: From To Transportation Notes Pudong International Laoximeng Station Shanghai Maglev Airport Direction: Longyang Road Longyang Road Station Yaohua Road Station Shanghai Metro Line 7 Transfer out Direction: Meilan Road of the station Yaohua Road Station Lianhang Road Station Shanghai Metro Line 8 Transfer Direction: Shendu Highway inside the station Lianhang Road Station SSC Walk (about 10 min, 500m) Accommodation Ji Hotel (60~100 USD per night) Address: No. -

Rolling Stock for Metro Railways
GOVERNMENT OF INDIA MINISTRY OF URBAN DEVELOPMENT REPORT OF THE SUB-COMMITTEE ON ROLLING STOCK FOR METRO RAILWAYS NOVEMBER 2013 2 Preface 1. Metro systems are already operational in Delhi and Bangalore and construction work is progressing at a fast pace in Chennai, Kolkata, Hyderabad, Jaipur, Kochi and Gurgaon. There are plans to have Metro Systems in cities with population more than 2 million. MOUD with a view to promote the domestic manufacturing for Metro Systems and formation of standards for such systems in India, has constituted a Group for preparing a Base paper on Standardization and Indigenization of Metro Railway Systems vide Order of F.No.K- 14011/26/2012 MRTS/Coord dated 30th May 2012. 2. The Group has identified certain issues which require detailed deliberations / review cost benefit analysis / study. The Group suggested that Sub-Committees may be constituted consisting of officers/professional drawn from relevant field/ profession from Ministry of Urban Development/Railways/Metros and industries associated with rail based systems / Metro Railway Systems. 3. Accordingly following Sub-Committees for various systems were constituted by Ministry of Urban Development vide order No. K-14011/26/2012-MRTS/Coorddt. 30.05.2012/25.07.2012: · Traction system · Rolling stock · Signaling system · Fare collection system · Operation & Maintenance · Track structure · Simulation Tools 4. The Sub-committee on Rolling Stock has following members: Shri Sanchit Pandey CGM/Rolling Stock/P/DMRC. Shri Amit Banerjee, GM/Technology Divn. BEML, Bangaluru. Shri Naresh Aggarwal, Chairman CII, Railway Equipment Divn. & MD & Co- Chairman, VAE, VKN Industries Pvt. Ltd. Shri Raminder Singh, Siemens Ltd. -

Pop / Rock / Commercial Music Wed, 25 Aug 2021 21:09:33 +0000 Page 1
Pop / Rock / Commercial music www.redmoonrecords.com Artist Title ID Format Label Print Catalog N° Condition Price Note 10000 MANIACS The wishing chair 19160 1xLP Elektra Warner GER 960428-1 EX/EX 10,00 € RE 10CC Look hear? 1413 1xLP Warner USA BSK3442 EX+/VG 7,75 € PRO 10CC Live and let live 6546 2xLP Mercury USA SRM28600 EX/EX 18,00 € GF-CC Phonogram 10CC Good morning judge 8602 1x7" Mercury IT 6008025 VG/VG 2,60 € \Don't squeeze me like… Phonogram 10CC Bloody tourists 8975 1xLP Polydor USA PD-1-6161 EX/EX 7,75 € GF 10CC The original soundtrack 30074 1xLP Mercury Back to EU 0600753129586 M-/M- 15,00 € RE GF 180g black 13 ENGINES A blur to me now 1291 1xCD SBK rec. Capitol USA 7777962072 USED 8,00 € Original sticker attached on the cover 13 ENGINES Perpetual motion 6079 1xCD Atlantic EMI CAN 075678256929 USED 8,00 € machine 1910 FRUITGUM Simon says 2486 1xLP Buddah Helidon YU 6.23167AF EX-/VG+ 10,00 € Verty little woc COMPANY 1910 FRUITGUM Simon says-The best of 3541 1xCD Buddha BMG USA 886972424422 12,90 € COMPANY 1910 Fruitgum co. 2 CELLOS Live at Arena Zagreb 23685 1xDVD Masterworks Sony EU 0888837454193 10,90 € 2 UNLIMITED Edge of heaven (5 vers.) 7995 1xCDs Byte rec. EU 5411585558049 USED 3,00 € 2 UNLIMITED Wanna get up (4 vers.) 12897 1xCDs Byte rec. EU 5411585558001 USED 3,00 € 2K ***K the millennium (3 7873 1xCDs Blast first Mute EU 5016027601460 USED 3,10 € Sample copy tracks) 2PLAY So confused (5 tracks) 15229 1xCDs Sony EU NMI 674801 2 4,00 € Incl."Turn me on" 360 GRADI Ba ba bye (4 tracks) 6151 1xCDs Universal IT 156 762-2 -
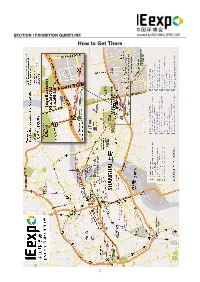
How to Get There
SECTION I EXHIBITION GUIDELINE How to Get There 12 SECTION I EXHIBITION GUIDELINE How to Get There (cont’d) Shanghai Metro Map 13 SECTION I EXHIBITION GUIDELINE How to Get There (cont’d) SNIEC is strategically located in Pudong‘s key economic development zone. There is a public traffic interchange for bus and metro, , one named “Longyang Road Station“ about 10-min walk from the station to fairground, and one named “Huamu Road Station“ about 1-min walk from the station to fairground. By flight The expo centre is located half way between Pudong International Airport and Hongqiao Airport, 35 km away from Pudong International Airport to the east, and 32 km away from Hongqiao Airport to the west. You can take the airport bus, maglev or metro directly to the expo center. From Pudong International Airport By taxi By Transrapid Maglev: from Pudong International Airport to Longyang Road Take metro line 2 to Longyang Road Station to change line 7 to Huamu Road Station, 60 min. By Airport Line Bus No. 3: from Pudong Int’l Airport to Longyang Road, 40 min, ca. RMB 20. From Hongqiao Airport By taxi Take metro line 2 to Longyang Road Station to change line 7 to Huamu Road Station, 60 min. By train From Shanghai Railway Station or Shanghai South Railway Station please take metro line1 to People’s Square, then take metro line 2 toward Pudong International Airport Station and get off at Longyang Road Station to change line7 to Huamu Road Station. From Hongqiao Railway Station, please take metro line 2 to Longyang Road Station and change line 7 to Huamu Road Station. -
112 It's Over Now 112 Only You 311 All Mixed up 311 Down
112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question -

Transportation Research Record No. 1489, Railroad Transportation Research
TRANSPORTATION RESEARCH RECORD No. 1489 Rail Railroad Transportation Research A peer-reviewed publication of the Transportation Research Board TRANSPORTATION RESEARCH BOARD NATIONAL RESEARCH COUNCIL NATIONAL ACADEMY PRESS WASHINGTON, D.C. 1995 Transportation Research Record 1489 Railway Systems Section ISSN 0361-1981 Chairman: A. J. Reinschmidt, Association of American Railroads ISBN 0-309-06155-5 Price: $26.00 Committee on Railroad Track Structure System Design Chairman: William H. Moorhead, Iron Horse Engineering Company, Inc. Subscriber Category Secretary: David C. Kelly, Illinois Central Railroad VII rail Ernest J. Barenberg, Dale K. Beachy, Harry Bressler, Ronald H. Dunn, Willem Ebersohn, Hugh J. Fuller, Stephen P. Heath, Crew S. Heimer, Printed in the United States of America Thomas B. Hutcheson, Amos Komornik, Myles E. Paisley, Jerry G. Rose, Ernest T. Selig, Joseph C. Sessa, Alfred E. Shaw, Jr., Thomas P. Smithberger, James W. Winger Committee on Electrification and Train Control Systems for Guided Sponsorship of Transportation Resear~h Record 1489 · Ground Transportation Systems Chairman: Paul H. Reisirup, Parsons Brinckerhoff International, Inc. GROUP I-TRANSPORTATION SYS.TEMS PLANNING AND Secretary: Paul K. Stangas, Edwards & Kelcey, Inc. ADMINISTRATION Kenneth W. Addison, John G. Bell, Peter A. Cannito, Richard U. Cogswell, Chairman: Thomas F. Humphrey, Massachusetts Institute of Technology Mary Ellen Fetchko, Allan C. Fisher, Jeffrey E. Gordon, Robert E. Heggestad, Stephen B. Kuznetsov, Robert H. Leilich, Thomas E. Margro, Multimodal Freight Transportation Section Robert W. McKnight, Howard G. Moody, Gordon B. Mott, Per-Erik Olson. Chairman: Anne Strauss-Wieder, Port Authority of New York William A. Petit, John A. Reach, Louis F. Sanders, Peter L. Shaw, Richard and New Jersey C. -

Bombardier Manufactures a Variety of Standalone Transit Systems, Including the INNOVIA Monorail, the INNOVIA APM, and the MOVIA Light Metro
Response to City of San Jose RFI 2019-DOT-PPD-4 New Transit Options: Airport-Diridon-Stevens Creek Transit Connection Bombardier manufactures a variety of standalone transit systems, including the INNOVIA Monorail, the INNOVIA APM, and the MOVIA Light Metro. All these systems, or a combination of these systems, could be an excellent basis for the Airport - Diridon - Steven's Creek corridor project(s). Of the three technologies, the INNOVIA Monorail appears to best address the objectives of the proposed project in that it is less expensive to construct, can be constructed more rapidly, and operates in a grade-separated, high capacity system. Ultimately the choice of technology depends on a variety of factors, most notably the planned ridership per hour, which are not available at present. As such, Bombardier has submitted information on all three technologies, and looks forward to the opportunity to discuss the best fit solution with the City of San Jose at their convenience. Bombardier anticipates that this project could be delivered as a Design-Build-Operate Maintain Finance (DBFOM) Public Private Partnership (PPP). Contact: Kevin Walker, Head of Ecosystem US West [email protected] (210) 781 9316 Bombardier Transportation (Holdings) USA Inc. 1501RFI 2019 LEBANON-DOT-PPD CHURCH-4 ROAD PITTSBURGH,New Transit Options: PA 15236 Airport -USADiridon -Stevens Creek Transit Connection Confidential and Proprietary Information Page | 1 New Transit Options: Airport-Diridon-Stevens Creek Transit Connection INNOVIA 300 APM Executive Summary With Automobile-based transportation reaching saturation in Silicon Valley, the City of San Jose is looking for sustainable transportation solutions which can be deployed quickly and cost effectively. -

The International Light Rail Magazine
THE INTERNATIONAL LIGHT RAIL MAGAZINE www.lrta.org www.tautonline.com FEBRUARY 2020 NO. 986 2020 VISION Our predictions for the new systems due to open this year Hamilton LRT cancellation ‘a betrayal’ Tram & metro: Doha’s double opening China launches 363km of new routes Berlin tramways Added value £4.60 Bringing Germany’s What is your tram capital back together project really worth? European Light Rail Congress TWO days of interactive debates... EIGHT hours of dedicated networking... ONE place to be Ibercaja Patio de la Infanta Zaragoza, Spain 10-11 June The European Light Rail Congress brings together leading opinion-formers and decision-makers from across Europe for two days of debate around the role of technology in the development of sustainable urban travel. With presentations and exhibitions from some of the industry’s most innovative suppliers and service providers, this congress also includes technical visits and over eight hours of networking sessions. 2020 For 2020, we are delighted to be holding the event in the beautiful city of Zaragoza in partnership with Tranvía Zaragoza, Mobility City and the Fundación Ibercaja. Our local partners at Tranvía Zaragoza have arranged a depot tour as part of day one’s activities at the European Light Rail Congress. At the event, attendees will discover the role and future of light rail within a truly intermodal framework. To submit an abstract or to participate, please contact Geoff Butler on +44 (0)1733 367610 or [email protected] +44 (0)1733 367600 @ [email protected] www.mainspring.co.uk MEDIA PARTNERS EU Light Rail Driving innovation CONTENTS The official journal of the Light Rail 64 Transit Association FEBRUARY 2020 Vol. -

Inside: Biffy Clyro Jantie Cullum Rishi Rich the Rapture Bob Marley Two-Track Low-Price Format Is Centrepiece of Major's Initiat
Inside: Biffy Clyro Jantie Cullum Rishi Rich The Rapture Bob Marley Two-track low-price format is centrepiece of major's initiative to revive flagging singles sales EMI unveils singles plan :k of clarity surrounding the approach to Windows. He eight tracks received 100 plays 01 _^^ingle fornm^as^rôf a dealer pricedto retlil at £2.99; or JdlsTg 0"^^ Sowwhyf9 ^Te^l^oth of prichtg and S^times on MTV Hite. " "g revmn^thesmg'esjnarket, ^ biggest-name artiste, dealer priced cial director, sales, Mike McMa- part of the OCC singles project, parallel announcement last week one th.rd dovvn on the year, EMI The new pnces ™., also conte not.ce of the changes front the groupsoverthe p^^ ' that ® See p4 and p7 Capital revamps to lift station Capital group puts new management team in place as the station regains the top spot in London listening p3 Virgin resliuffie to boost genres Retail giant reorganises buying teams to maximise its strength in specialist music and to react to tough market p4 IOTP: Wre stayïng on BBCF BBC entertainmentboss backs top pop show, as Cowey cites "musical différences" for his shock departurepô This week's Number Is ASbums: TSie Coral Texas album SlngSes: B9ii Caiiirell Airplay: Beycncé 9 "776669 '77609 09.08.03/£4.00 © Action needs to be taken quickly. There is no time to wait until after a busy autumn; the time is now' - Editorial, pl4 Your guide to the latest news from the music industry lin his European responsibilitie withfourth 6.0%, with while12.5% Windswept and Sony/ATV finished fifth tie-up with WMI's lav nd corporate aflairs.