DOCSLIB.ORG

Basics of UNIX

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Basics of UNIX Basics of UNIX August 23, 2012 By UNIX, I mean any UNIX-like operating system, including Linux and Mac OS X. On the Mac you can access a UNIX terminal window with the Terminal application (under Applica- tions/Utilities). Most modern scientific computing is done on UNIX-based machines, often by remotely logging in to a UNIX-based server. 1 Connecting to a UNIX machine from {UNIX, Mac, Windows} See the file on bspace on connecting remotely to SCF. In addition, this SCF help page has infor- mation on logging in to remote machines via ssh without having to type your password every time. This can save a lot of time. 2 Getting help from SCF More generally, the department computing FAQs is the place to go for answers to questions about SCF. For questions not answered there, the SCF requests: “please report any problems regarding equipment or system software to the SCF staff by sending mail to ’trouble’ or by reporting the prob- lem directly to room 498/499. For information/questions on the use of application packages (e.g., R, SAS, Matlab), programming languages and libraries send mail to ’consult’. Questions/problems regarding accounts should be sent to ’manager’.” Note that for the purpose of this class, questions about application packages, languages, li- braries, etc. can be directed to me. 1 3 Files and directories 1. Files are stored in directories (aka folders) that are in a (inverted) directory tree, with “/” as the root of the tree 2. Where am I? > pwd 3. What’s in a directory? > ls > ls -a > ls -al 4. Moving around > cd /home/paciorek/teaching/243 > cd ~paciorek/teaching/243 > cd ~/teaching/243 > cd 243 # provided I am in ’teaching’ > cd .. > cd - 5. Copying and removing > cp > cp -r > cp -rp # preserves timestamps and other metainfo (VERY handy for tracing your workflows if you move files between machines) > mkdir > rm > rm -r > rm -rf # CAREFUL! To copy between machines, we can use scp, which has similar options to cp: > scp file.txt [email protected]:~/research/. > scp [email protected]:/data/file.txt ~/research/renamed.txt 2 6. File permissions: ls -al will show the permissions for the ’user’, ’group’, ’other’ • to allow a file to be executed as a program: > chmod ugo+x myProg # myProg should be compiled code or a shell script • to allow read and write access to all: > chmod ugo+rw code.q • to prevent write access: > chmod go-w myThesisCode.q 7. Compressing files • the zip utility compresses in a format compatible with zip files for Windows: > zip files.zip a.txt b.txt c.txt • gzip is the standard in UNIX: > gzip a.txt b.txt c.txt # will create a.txt.gz, b.txt.gz, c.txt.gz • tar will nicely wrap up entire directories: > tar -cvf files.tar myDirectory > tar -cvzf files.tgz myDirectory • To unwrap a tarball > tar -xvf files.tar > tar -xvzf files.tgz • To peek into a zipped (text) file: > gzip -cd file.gz | less > zcat file.zip | less 4 A variety of UNIX tools/capabilities Many UNIX programs are small programs (tools, utilities) that can be combined to do complicated things. 1. For help on a UNIX program, including command-line utilities like ls, cp, etc. > man cp 3 2. What’s the path of an executable? > which R 3. Tools for remotely mounting the filesystem of a remote UNIX machine/filesystem as a ’local’ directory on your machine: • Samba protocol - see “How can I mount my home directory” on SCF Help Desk FAQs • MacFUSE • Linux: > cd; mkdir nersc # create a directory as a mountpoint > sshfs carver.nersc.gov: /Users/paciorek/nersc # mount the remote filesystem > fusermount -u ~/scf # to unmount 4. Cloud storage: Dropbox and other services will mirror directories on multiple machines and on their servers 5. To do something at the UNIX command line from within R, use the system() function in R: > system(“ls -al”) 6. Editors For statistical computing, we need an editor, not a word processor, because we’re going to be operating on files of code and data files, for which word processing formatting gets in the way. • traditional UNIX: emacs, vi • Windows: WinEdt • Mac: Aquamacs Emacs, TextMate, TextEdit • Be careful in Windows - file suffixes are often hidden 7. Basic emacs: • emacs has special modes for different types of files: R code files, C code files, Latex files – it’s worth your time to figure out how to set this up on your machine for the kinds of files you often work on 4 Table 1. Helpful emacs control sequences. Sequence Result C-x,C-c Close the file C-x,C-s Save the file C-x,C-w Save with a new name C-s Search ESC Get out of command buffer at bottom of screen C-a Go to beginning of line C-e Go to end of line C-k Delete the rest of the line from cursor forward C-space, then move to end of block Highlight a block of text C-w Remove the highlighted block, putting it in the kill buffer C-y (after using C-k or C-w) Paste from kill buffer (’y’ is for ’yank’) – For working with R, ESS (emacs speaks statistics) mode is helpful. This is built in to Aquamacs emacs. Alternatively, the Windows and Mac versions of R, as well as RStudio (available for all platforms) provide a GUI with a built-in editor. • To open emacs in the terminal window rather than as a new window, which is handy when it’s too slow (or impossible) to tunnel the graphical emacs window through ssh: > emacs -nw file.txt 8. Files that provide info about a UNIX machine: • /proc/meminfo • /proc/cpuinfo • /etc/issue • Example: how do I find out how many processors a machine has: > grep processor /proc/cpuinfo 9. There are (free) tools in UNIX to convert files between lots of formats (pdf, ps, html, latex, jpg). This is particularly handy when preparing figures for a publication. My computing tips page lists a number of these. 5 The bash shell and UNIX utilities August 26, 2012 Sections with more advanced material that are not critical for those of you just getting started with UNIX are denoted (***). However, I will ask you to write a shell function on the first problem set. Note that it can be difficult to distinguish what is shell-specific and what is just part of UNIX. Some of the material here is not bash-specific but general to UNIX. Reference: Newham and Rosenblatt, Learning the bash Shell, 2nd ed. 1 Shell basics The shell is the interface between you and the UNIX operating system. When you are working in a terminal window (i.e., a window with the command line interface), you’re interacting with a shell. There are multiple shells (sh, bash, csh, tcsh, ksh). We’ll assume usage of bash, as this is the default for Mac OSX and on the SCF machines and is very common for Linux. 1. What shell am I using? > echo $SHELL 2. To change to bash on a one-time basis: > bash 3. To make it your default: > chsh /bin/bash /bin/bash should be whatever the path to the bash shell is, which you can figure out using which bash Shell commands can be saved in a file (with extension .sh) and this file can be executed as if it were a program. To run a shell script called file.sh, you would type ./file.sh. Note that if you just typed file.sh, the shell will generally have trouble finding the script and recognizing that it is executable. 1 2 Tab completion When working in the shell, it is often unnecessary to type out an entire command or file name, because of a feature known as tab completion. When you are entering a command or filename in the shell, you can, at any time, hit the tab key, and the shell will try to figure out how to complete the name of the command or filename you are typing. If there is only one command in the search path and you’re using tab completion with the first token of a line, then the shell will display its value and the cursor will be one space past the completed name. If there are multiple commands that match the partial name, the shell will display as much as it can. In this case, hitting tab twice will display a list of choices, and redisplay the partial command line for further editing. Similar behavior with regard to filenames occurs when tab completion is used on anything other than the first token of a command. Note that R does tab completion for objects (including functions) and filenames. 3 Command history By using the up and down arrows, you can scroll through commands that you have entered previ- ously. So if you want to rerun the same command, or fix a typo in a command you entered, just scroll up to it and hit enter to run it or edit the line and then hit enter. Note that you can use emacs-like control sequences (C-a, C-e, C-k) to navigate and delete characters, just as you can at the prompt in the shell usually. You can also rerun previous commands as follows: > !-n # runs the nth previous command > !xt # runs the last command that started with ’xt’ If you’re not sure what command you’re going to recall, you can append :p at the end of the text you type to do the recall, and the result will be printed, but not executed.
Load more

Recommended publications
  • Unix Introduction
    Unix introduction Mikhail Dozmorov Summer 2018 Mikhail Dozmorov Unix introduction Summer 2018 1 / 37 What is Unix Unix is a family of operating systems and environments that exploits the power of linguistic abstractions to perform tasks Unix is not an acronym; it is a pun on “Multics”. Multics was a large multi-user operating system that was being developed at Bell Labs shortly before Unix was created in the early ’70s. Brian Kernighan is credited with the name. All computational genomics is done in Unix http://www.read.seas.harvard.edu/~kohler/class/aosref/ritchie84evolution.pdfMikhail Dozmorov Unix introduction Summer 2018 2 / 37 History of Unix Initial file system, command interpreter (shell), and process management started by Ken Thompson File system and further development from Dennis Ritchie, as well as Doug McIlroy and Joe Ossanna Vast array of simple, dependable tools that each do one simple task Ken Thompson (sitting) and Dennis Ritchie working together at a PDP-11 Mikhail Dozmorov Unix introduction Summer 2018 3 / 37 Philosophy of Unix Vast array of simple, dependable tools Each do one simple task, and do it really well By combining these tools, one can conduct rather sophisticated analyses The Linux help philosophy: “RTFM” (Read the Fine Manual) Mikhail Dozmorov Unix introduction Summer 2018 4 / 37 Know your Unix Unix users spend a lot of time at the command line In Unix, a word is worth a thousand mouse clicks Mikhail Dozmorov Unix introduction Summer 2018 5 / 37 Unix systems Three common types of laptop/desktop operating systems: Windows, Mac, Linux. Mac and Linux are both Unix-like! What that means for us: Unix-like operating systems are equipped with “shells”" that provide a command line user interface.
    [Show full text]
  • Administering Unidata on UNIX Platforms
    C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta UniData Administering UniData on UNIX Platforms UDT-720-ADMU-1 C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Notices Edition Publication date: July, 2008 Book number: UDT-720-ADMU-1 Product version: UniData 7.2 Copyright © Rocket Software, Inc. 1988-2010. All Rights Reserved. Trademarks The following trademarks appear in this publication: Trademark Trademark Owner Rocket Software™ Rocket Software, Inc. Dynamic Connect® Rocket Software, Inc. RedBack® Rocket Software, Inc. SystemBuilder™ Rocket Software, Inc. UniData® Rocket Software, Inc. UniVerse™ Rocket Software, Inc. U2™ Rocket Software, Inc. U2.NET™ Rocket Software, Inc. U2 Web Development Environment™ Rocket Software, Inc. wIntegrate® Rocket Software, Inc. Microsoft® .NET Microsoft Corporation Microsoft® Office Excel®, Outlook®, Word Microsoft Corporation Windows® Microsoft Corporation Windows® 7 Microsoft Corporation Windows Vista® Microsoft Corporation Java™ and all Java-based trademarks and logos Sun Microsystems, Inc. UNIX® X/Open Company Limited ii SB/XA Getting Started The above trademarks are property of the specified companies in the United States, other countries, or both. All other products or services mentioned in this document may be covered by the trademarks, service marks, or product names as designated by the companies who own or market them. License agreement This software and the associated documentation are proprietary and confidential to Rocket Software, Inc., are furnished under license, and may be used and copied only in accordance with the terms of such license and with the inclusion of the copyright notice.
    [Show full text]
  • Introduction to Command Line and Accessing Servers Remotely
    Introduction to command line and accessing servers remotely Marco Büchler, Emily Franzini, Greta Franzini, Maria Moritz eTRAP Research Group Göttingen Centre for Digital Humanities Institute of Computer Science Georg August University Göttingen, Germany DH Estonia 2015 - Text Reuse Hackathon 20. Oktober 2015 Who am I? • 2001/2 Head of Quality Assurance department in a software company • 2006 Diploma in Computer Science on big • scale co-occurrence analysis • 2007- Consultant for several SMEs in IT sector • 2008 Technical project management of eAQUA project • 2011 PI and project manager of eTRACES project • 2013 PhD in „Digital Humanities“ on Text Reuse • 2014- Head of Early Career Research Group eTRAP at Göttingen Centre for Digital Humanities DH Estonia 2015 - Text Reuse Hackathon 20. Oktober 2015 Agenda 1) Connecting to the server 2) Some command line introduction DH Estonia 2015 - Text Reuse Hackathon 20. Oktober 2015 Connecting to the server 1) Windows: Start Putty 2) Mac + Linux: Open a terminal 3) Connecting to server via ssh -l <login> 192.168.11.4 4) Enter password DH Estonia 2015 - Text Reuse Hackathon 20. Oktober 2015 Which folder am I on the server? Command: pwd (parent working directory) Usage: pwd <ENTER> Example: pwd <ENTER> DH Estonia 2015 - Text Reuse Hackathon 20. Oktober 2015 Which files and directories are contained in my pwd? Command: ls (list) Usage: ls -l <FOLDER> <ENTER> // list all files and directory one on each line ls -la <FOLDER> <ENTER> // show also hidden files ls -lh <FOLDER> <ENTER> // show e.g. files sizes in human- friendly version Example: ls -l <ENTER> ls -lh /home/mbuechler <ENTER> DH Estonia 2015 - Text Reuse Hackathon 20.
    [Show full text]
  • Types and Programming Languages by Benjamin C
    < Free Open Study > . .Types and Programming Languages by Benjamin C. Pierce ISBN:0262162091 The MIT Press © 2002 (623 pages) This thorough type-systems reference examines theory, pragmatics, implementation, and more Table of Contents Types and Programming Languages Preface Chapter 1 - Introduction Chapter 2 - Mathematical Preliminaries Part I - Untyped Systems Chapter 3 - Untyped Arithmetic Expressions Chapter 4 - An ML Implementation of Arithmetic Expressions Chapter 5 - The Untyped Lambda-Calculus Chapter 6 - Nameless Representation of Terms Chapter 7 - An ML Implementation of the Lambda-Calculus Part II - Simple Types Chapter 8 - Typed Arithmetic Expressions Chapter 9 - Simply Typed Lambda-Calculus Chapter 10 - An ML Implementation of Simple Types Chapter 11 - Simple Extensions Chapter 12 - Normalization Chapter 13 - References Chapter 14 - Exceptions Part III - Subtyping Chapter 15 - Subtyping Chapter 16 - Metatheory of Subtyping Chapter 17 - An ML Implementation of Subtyping Chapter 18 - Case Study: Imperative Objects Chapter 19 - Case Study: Featherweight Java Part IV - Recursive Types Chapter 20 - Recursive Types Chapter 21 - Metatheory of Recursive Types Part V - Polymorphism Chapter 22 - Type Reconstruction Chapter 23 - Universal Types Chapter 24 - Existential Types Chapter 25 - An ML Implementation of System F Chapter 26 - Bounded Quantification Chapter 27 - Case Study: Imperative Objects, Redux Chapter 28 - Metatheory of Bounded Quantification Part VI - Higher-Order Systems Chapter 29 - Type Operators and Kinding Chapter 30 - Higher-Order Polymorphism Chapter 31 - Higher-Order Subtyping Chapter 32 - Case Study: Purely Functional Objects Part VII - Appendices Appendix A - Solutions to Selected Exercises Appendix B - Notational Conventions References Index List of Figures < Free Open Study > < Free Open Study > Back Cover A type system is a syntactic method for automatically checking the absence of certain erroneous behaviors by classifying program phrases according to the kinds of values they compute.
    [Show full text]
  • LATEX for Beginners
    LATEX for Beginners Workbook Edition 5, March 2014 Document Reference: 3722-2014 Preface This is an absolute beginners guide to writing documents in LATEX using TeXworks. It assumes no prior knowledge of LATEX, or any other computing language. This workbook is designed to be used at the `LATEX for Beginners' student iSkills seminar, and also for self-paced study. Its aim is to introduce an absolute beginner to LATEX and teach the basic commands, so that they can create a simple document and find out whether LATEX will be useful to them. If you require this document in an alternative format, such as large print, please email [email protected]. Copyright c IS 2014 Permission is granted to any individual or institution to use, copy or redis- tribute this document whole or in part, so long as it is not sold for profit and provided that the above copyright notice and this permission notice appear in all copies. Where any part of this document is included in another document, due ac- knowledgement is required. i ii Contents 1 Introduction 1 1.1 What is LATEX?..........................1 1.2 Before You Start . .2 2 Document Structure 3 2.1 Essentials . .3 2.2 Troubleshooting . .5 2.3 Creating a Title . .5 2.4 Sections . .6 2.5 Labelling . .7 2.6 Table of Contents . .8 3 Typesetting Text 11 3.1 Font Effects . 11 3.2 Coloured Text . 11 3.3 Font Sizes . 12 3.4 Lists . 13 3.5 Comments & Spacing . 14 3.6 Special Characters . 15 4 Tables 17 4.1 Practical .
    [Show full text]
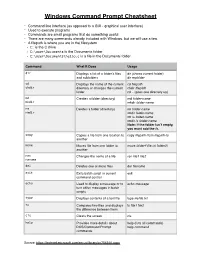
  • Windows Command Prompt Cheatsheet
    Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx.
    [Show full text]
  • The Gnu Binary Utilities
    The gnu Binary Utilities Version cygnus-2.7.1-96q4 May 1993 Roland H. Pesch Jeffrey M. Osier Cygnus Support Cygnus Support TEXinfo 2.122 (Cygnus+WRS) Copyright c 1991, 92, 93, 94, 95, 1996 Free Software Foundation, Inc. Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are preserved on all copies. Permission is granted to copy and distribute modi®ed versions of this manual under the conditions for verbatim copying, provided also that the entire resulting derived work is distributed under the terms of a permission notice identical to this one. Permission is granted to copy and distribute translations of this manual into another language, under the above conditions for modi®ed versions. The GNU Binary Utilities Introduction ..................................... 467 1ar.............................................. 469 1.1 Controlling ar on the command line ................... 470 1.2 Controlling ar with a script ............................ 472 2ld.............................................. 477 3nm............................................ 479 4 objcopy ....................................... 483 5 objdump ...................................... 489 6 ranlib ......................................... 493 7 size............................................ 495 8 strings ........................................ 497 9 strip........................................... 499 Utilities 10 c++®lt ........................................ 501 11 nlmconv ....................................
    [Show full text]
  • Creating Rpms Guide
    CREATING RPMS (Student version) v1.0 Featuring 36 pages of lecture and a 48 page lab exercise This docu m e n t serves two purpose s: 1. Representative sample to allow evaluation of our courseware manuals 2. Make available high quality RPM documentation to Linux administrators A bout this m aterial : The blue background you see simulates the custom paper that all Guru Labs course w are is printed on. This student version does not contain the instructor notes and teaching tips present in the instructor version. For more information on all the features of our unique layout, see: http://ww w . g urulabs.co m /courseware/course w are_layout.php For more freely available Guru Labs content (and the latest version of this file), see: http://www.gurulabs.co m/goodies/ This sample validated on: Red Hat Enterprise Linux 4 & Fedora Core v3 SUSE Linux Enterprise Server 9 & SUSE Linux Professional 9.2 About Guru Labs: Guru Labs is a Linux training company started in 199 9 by Linux experts to produce the best Linux training and course w are available. For a complete list, visit our website at: http://www.gurulabs.co m/ This work is copyrighted Guru Labs, L.C. 2005 and is licensed under the Creative Common s Attribution- NonCom mer cial- NoDerivs License. To view a copy of this license, visit http://creativecom m o n s.org/licenses/by- nc- nd/2.0/ or send a letter to Creative Commons, 559 Nathan Abbott Way, Stanford, California 943 0 5, USA. Guru Labs 801 N 500 W Ste 202 Bountiful, UT 84010 Ph: 801-298-5227 WWW.GURULABS.COM Objectives: • Understand
    [Show full text]
  • Download the Specification
    Internationalizing and Localizing Applications in Oracle Solaris Part No: E61053 November 2020 Internationalizing and Localizing Applications in Oracle Solaris Part No: E61053 Copyright © 2014, 2020, Oracle and/or its affiliates. License Restrictions Warranty/Consequential Damages Disclaimer This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. Warranty Disclaimer The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. Restricted Rights Notice If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs) and Oracle computer documentation or other Oracle data delivered to or accessed by U.S. Government end users are "commercial
    [Show full text]
  • A Large-Scale Study of File-System Contents
    A Large-Scale Study of File-System Contents John R. Douceur and William J. Bolosky Microsoft Research Redmond, WA 98052 {johndo, bolosky}@microsoft.com ABSTRACT sizes are fairly consistent across file systems, but file lifetimes and file-name extensions vary with the job function of the user. We We collect and analyze a snapshot of data from 10,568 file also found that file-name extension is a good predictor of file size systems of 4801 Windows personal computers in a commercial but a poor predictor of file age or lifetime, that most large files are environment. The file systems contain 140 million files totaling composed of records sized in powers of two, and that file systems 10.5 TB of data. We develop analytical approximations for are only half full on average. distributions of file size, file age, file functional lifetime, directory File-system designers require usage data to test hypotheses [8, size, and directory depth, and we compare them to previously 10], to drive simulations [6, 15, 17, 29], to validate benchmarks derived distributions. We find that file and directory sizes are [33], and to stimulate insights that inspire new features [22]. File- fairly consistent across file systems, but file lifetimes vary widely system access requirements have been quantified by a number of and are significantly affected by the job function of the user. empirical studies of dynamic trace data [e.g. 1, 3, 7, 8, 10, 14, 23, Larger files tend to be composed of blocks sized in powers of two, 24, 26]. However, the details of applications’ and users’ storage which noticeably affects their size distribution.
    [Show full text]
  • Unix/Linux Command Reference
    Unix/Linux Command Reference .com File Commands System Info ls – directory listing date – show the current date and time ls -al – formatted listing with hidden files cal – show this month's calendar cd dir - change directory to dir uptime – show current uptime cd – change to home w – display who is online pwd – show current directory whoami – who you are logged in as mkdir dir – create a directory dir finger user – display information about user rm file – delete file uname -a – show kernel information rm -r dir – delete directory dir cat /proc/cpuinfo – cpu information rm -f file – force remove file cat /proc/meminfo – memory information rm -rf dir – force remove directory dir * man command – show the manual for command cp file1 file2 – copy file1 to file2 df – show disk usage cp -r dir1 dir2 – copy dir1 to dir2; create dir2 if it du – show directory space usage doesn't exist free – show memory and swap usage mv file1 file2 – rename or move file1 to file2 whereis app – show possible locations of app if file2 is an existing directory, moves file1 into which app – show which app will be run by default directory file2 ln -s file link – create symbolic link link to file Compression touch file – create or update file tar cf file.tar files – create a tar named cat > file – places standard input into file file.tar containing files more file – output the contents of file tar xf file.tar – extract the files from file.tar head file – output the first 10 lines of file tar czf file.tar.gz files – create a tar with tail file – output the last 10 lines
    [Show full text]
  • Your Performance Task Summary Explanation
    Lab Report: 11.2.5 Manage Files Your Performance Your Score: 0 of 3 (0%) Pass Status: Not Passed Elapsed Time: 6 seconds Required Score: 100% Task Summary Actions you were required to perform: In Compress the D:\Graphics folderHide Details Set the Compressed attribute Apply the changes to all folders and files In Hide the D:\Finances folder In Set Read-only on filesHide Details Set read-only on 2017report.xlsx Set read-only on 2018report.xlsx Do not set read-only for the 2019report.xlsx file Explanation In this lab, your task is to complete the following: Compress the D:\Graphics folder and all of its contents. Hide the D:\Finances folder. Make the following files Read-only: D:\Finances\2017report.xlsx D:\Finances\2018report.xlsx Complete this lab as follows: 1. Compress a folder as follows: a. From the taskbar, open File Explorer. b. Maximize the window for easier viewing. c. In the left pane, expand This PC. d. Select Data (D:). e. Right-click Graphics and select Properties. f. On the General tab, select Advanced. g. Select Compress contents to save disk space. h. Click OK. i. Click OK. j. Make sure Apply changes to this folder, subfolders and files is selected. k. Click OK. 2. Hide a folder as follows: a. Right-click Finances and select Properties. b. Select Hidden. c. Click OK. 3. Set files to Read-only as follows: a. Double-click Finances to view its contents. b. Right-click 2017report.xlsx and select Properties. c. Select Read-only. d. Click OK. e.
    [Show full text]