Zone-Based, Robust Flood Evacuation Planning$
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
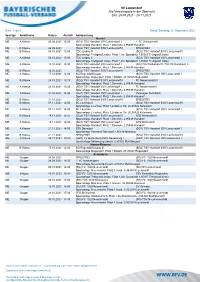
SV Lanzendorf Alle Vereinsspiele in Der Übersicht Zeit: 08.08
SV Lanzendorf Alle Vereinsspiele in der Übersicht Zeit: 25.09.2021 - 28.11.2021 Seite 1 von 3 Stand: Samstag, 25. September 2021 Spieltyp Spielklasse Datum Anstoß Spielpaarung Herren ME A Klasse 26.09.2021 15:30 (SG1) TSV Harsdorf I/SV Lanzendorf I 1. FC Schwarzach Sportanlage Harsdorf, Platz 1,Oberlohe 2,95499 Harsdorf ME B Klasse 26.09.2021 (SG2) TSV Harsdorf II/SV Lanzendorf II SPIELFREI ME B Klasse 03.10.2021 13:00 TDC Lindau III (SG2) TSV Harsdorf II/SV Lanzendorf II Sportanlage Trebgast/Lindau, Platz 1,Am Sportplatz 1,95367 Trebgast/Lindau ME A Klasse 03.10.2021 15:00 TDC Lindau II (SG1) TSV Harsdorf I/SV Lanzendorf I Sportanlage Trebgast/Lindau, Platz 1,Am Sportplatz 1,95367 Trebgast/Lindau ME A Klasse 10.10.2021 15:30 (SG1) TSV Harsdorf I/SV Lanzendorf I (SG) TSV Melkendorf I/ TSV 08 Kulmbach II Sportanlage Harsdorf, Platz 1,Oberlohe 2,95499 Harsdorf ME B Klasse 10.10.2021 (SG2) TSV Harsdorf II/SV Lanzendorf II SPIELFREI ME A Klasse 17.10.2021 14:00 SG Rugendorf/Losau (SG1) TSV Harsdorf I/SV Lanzendorf I Sportanlage Rugendorf, Platz 1,Badstr. 27,95365 Rugendorf ME B Klasse 24.10.2021 13:15 (SG2) TSV Harsdorf II/SV Lanzendorf II FC Neuenmarkt III Sportanlage Harsdorf, Platz 1,Oberlohe 2,95499 Harsdorf ME A Klasse 24.10.2021 15:30 (SG1) TSV Harsdorf I/SV Lanzendorf I FC Neuenmarkt II Sportanlage Harsdorf, Platz 1,Oberlohe 2,95499 Harsdorf ME A Klasse 31.10.2021 14:30 (SG1) TSV Harsdorf I/SV Lanzendorf I Vatanspor Kulmbach Sportanlage Harsdorf, Platz 1,Oberlohe 2,95499 Harsdorf ME B Klasse 31.10.2021 (SG2) TSV Harsdorf II/SV Lanzendorf II SPIELFREI ME B Klasse 07.11.2021 12:00 BC Leuchau II (SG2) TSV Harsdorf II/SV Lanzendorf II Sportanlage Leuchau, Platz 1,Lindauer Str. -

Beyond the Boat
Beyond the Boat RIVER CRUISE EXTENSION TOURS Welcome! We know the gift of travel is a valuable experience that connects people and places in many special ways. When tourism closed its doors during the difficult months of the COVID-19 outbreak, Germany ranked as the second safest country in the world by the London Deep Knowled- ge Group, furthering its trust as a destination. When you are ready to explore, river cruises continue to be a great way of traveling around Germany and this handy brochure provides tour ideas for those looking to venture beyond the boat or plan a stand-alone dream trip to Bavaria. The special tips inside capture the spirit of Bavaria – traditio- nally different and full of surprises. Safe travel planning! bavaria.by/rivercruise facebook.com/visitbavaria instagram.com/bayern Post your Bavarian experiences at #visitbavaria. Feel free to contact our US-based Bavaria expert Diana Gonzalez: [email protected] TIP: Stay up to date with our trade newsletter. Register at: bavaria.by/newsletter Publisher: Photos: p. 1: istock – bkindler | p. 2: BayTM – Peter von Felbert, Gert Krautbauer | p. 3: BayTM – Peter von Felbert, fotolia – BAYERN TOURISMUS herculaneum79 | p. 4/5: BayTM – Peter von Felbert | p. 6: BayTM – Gert Krautbauer | p. 7: BayTM – Peter von Felbert, Gert Kraut- Marketing GmbH bauer (2), Gregor Lengler, Florian Trykowski (2), Burg Rabenstein | p. 8: BayTM – Gert Krautbauer | p. 9: FC Bayern München, Arabellastr. 17 Burg Rabenstein, fotolia – atira | p. 10: BayTM – Peter von Felbert | p. 11: Käthe Wohlfahrt | p. 12: BayTM – Jan Greune, Gert Kraut- 81925 Munich, Germany bauer | p. -

SSV Kasendorf Gegen TSV Kirchenlaibach- Speichersdorf
Saison 2012/2013 Bezirksliga Oberfranken ost Kreisklasse Kulmbach aktuell 327/06 Kerwa-Sonntag 23. September 2012, 15.00 Uhr SSV Kasendorf gegen TSV Kirchenlaibach- Speichersdorf Sturmtank Andy Pistor versucht trotz Foul noch an seinem Steinbach- Dürrenwaider Gegenspieler vorbeizuziehen. Zum heutigen Spiel Wir begrüßen Sie am Kirchweihwochenende Punkt bangen, als die Steinberger eine klare im Namen des SSV Kasendorf ganz herzlich Möglichkeit vergaben. zur Bezirksoberligabegegnung gegen den Heute begrüßen wir mit dem TSV Kirchenlai- TSV Kirchenlaibach-Speichersdorf auf dem bach-Speichersdorf eine Mannschaft, die mit 16 Bernhard-Münch-Sportgelände. Ein besonderer Punkten im vorderen Mittelfeld zu finden ist. Willkommensgruß gilt dabei unseren Gästen Unsere Gäste hatten einen sehr erfolgreichen mit seinen Aktiven, Betreuern und Anhängern, Saisonstart und lagen nach fünf Spieltagen in sowie dem Schiedsrichter Felix Hoffmann mit der Spitzengruppe, mussten danach allerdings seinen Assistenten. drei Niederlagen in Folge hinnehmen. Im letz- Im Moment ist es schon verhext. In den letzten ten Heimspiel wurde aber der SV Steinmühle beiden Spielen waren durchaus sechs Punkte klar mit 4:1 geschlagen. Dass dieser Trend drin. Trotzdem musste sich unser SSV mit nicht anhält liegt nun an unserer Truppe. Mit einem mageren Pünktchen zufriedengeben. den zuletzt gezeigten Leistungen unserer Jungs Überraschenderweise beherrschten wir beim und den nötigen Quäntchen Glück scheint dies letzten Heimspiel den Tabellenführer aus nicht unmöglich. Steinbach-Dürrenwaid über weite Strecken Wir wünschen den beiden Mannschaften und hatten etliche „Hundertprozentige“. Doch ein verletzungsfreies und faires Spiel, dem im Abschluss versagten uns öfters die Nerven Schiedsrichtergespann jederzeit den richtigen und ein schmeichelhafter 0:1 Gästesieg stand Pfiff, und unserem SSV viel Erfolg damit der zu Buche. -

Business Bavaria Newsletter
Business Bavaria Newsletter Issue 07/08 | 2013 What’s inside 5 minutes with … Elissa Lee, Managing Director of GE Aviation, Germany Page 2 In focus: Success of vocational training Page 3 Bavaria in your Briefcase: Summer Architecture award for tourism edition Page 4 July/August 2013 incl. regional special Upper Franconia Apprenticeships – a growth market Bavaria’s schools are known for their well-trained school leavers. In July, a total of According to the latest education monitoring publication of the Initiative Neue 130,000 young Bavarians start their careers. They can choose from a 2% increase Soziale Marktwirtschaft, Bavaria is “top when it comes to school quality and ac- in apprenticeships compared to the previous year. cess to vocational training”. More and more companies are increasing the number of training positions to promote young people and thus lay the foundations for With 133,000 school leavers, 2013 has a sizeable schooled generation. Among long-term success. the leavers are approximately 90,000 young people who attended comprehensive school for nine years or grammar school for ten. Following their vocational train- The most popular professions among men and women are very different in Ba- ing, they often start their apprenticeships right away. varia: while many male leavers favour training as motor or industrial mechanics To ensure candidates and positions are properly matched, applicants and com- or retail merchants, occupations such as office manager, medical specialist and panies seeking apprentices are supported in their search by the Employment retail expert are the most popular choices among women. Agency. Between October 2012 and June 2013 companies made a total of 88,541 free, professional, training places available – an increase of 1.8% on the previ- www.ausbildungsoffensive-bayern.de ous year. -

Frankenwaldtag in Grafengehaig
Jahrgang 35 Mittwoch, den 7. Mai 2014 Nummer 5 Frankenwaldtag in Grafengehaig Der Obmann der Zeyerner Ortsgruppe des Fran- kenwaldvereins, Werner Hempfling (Vierter von rechts), übergab den Hauptwanderwimpel an den Hauptvorsitzenden Robert Strobel (Zwei- ter von rechts). Mit im Bild von links die Obfrau der Grafengehaiger Ortsgruppe Margitta Hieke, Bürgermeister Werner Burger, Josef Huber und Baron Ludwig von Lerchenfeld. Im Obergeschoss des hervorragend reno- vierten Mesnerhauses lauschten die geladenen Gäste den Ausführungen von Bürgermeister Werner Burger (links). Mit im Bild von rechts Landtagsabgeordneter Baron Ludwig von Lerchenfeld, die Obfrau der Ortsgruppe Gra- fengehaig, Margitta Hieke, stellvertretender Hauptvorsitzender Dieter Frank und Haupt- vorsitzenden Robert Strobel. Bericht siehe Innenteil Mitteilungsblatt Marktleugast und Grafengehaig - 2 - Nr. 5/14 Bekanntmachungen Telefonverzeichnis der Verwaltungsgemeinschaft Marktleugast Name Zimmer Durchwahl E-Mail-Adresse Uome, Franz Erster Bürgermeister Markt Marktleugast 4 947- 12 [email protected] Burger, Werner Erster Bürgermeister Markt Grafengehaig 4 3 55 in Grafengehaig 947-17 in Mlg. [email protected] Laaber, Michael Geschäftsstellenleiter 4 947-13 [email protected] Bittermann, Siegrid Sekretariat 4 947- 0 Dienstzeiten [email protected] Weber, Kathrin der Verwaltungsgemeinschaft Marktleugast: Neuensorger Bauverwaltung 3 947-14 Weg 10 [email protected] Montag bis Freitag von ............................... 08:00 bis 12:00 Uhr Taig, Norbert -

BEGR Ü NDUNG Bebauungsplan Mit Integriertem
Begründung zum Bebauungsplan und Flächennutzungsplan mit integriertem Grünordnungsplan B 41 „Lärchenweg” für ein allgemeines Wohngebiet im OT Reundorf der Stadt Lichtenfels, Lkr. Lichtenfels B E G R Ü N D U N G Bebauungsplan mit integriertem Grünordnungsplan mit Änderung des Flächennutzungsplanes B 41 “Lärchenweg” im OT Reundorf Begründung zum Bebauungsplan und Flächennutzungsplan mit integriertem Grünordnungsplan B 41 „Lärchenweg” für ein allgemeines Wohngebiet im OT Reundorf der Stadt Lichtenfels, Lkr. Lichtenfels Vorhabensträger: Stadt Lichtenfels Marktplatz 1+ 5, 96215 Lichtenfels Ansprechpartner: Stadtbauamt Lichtenfels Datum: 26.10.2019 Entwurfsverfasser: Stadt Lichtenfels Marktplatz 1 + 5, 96215 Lichtenfels Ansprechpartner: Stadtbauamt Lichtenfels Begründung zum Bebauungsplan und Flächennutzungsplan mit integriertem Grünordnungsplan B 41 „Lärchenweg” für ein allgemeines Wohngebiet im OT Reundorf der Stadt Lichtenfels, Lkr. Lichtenfels I N H A L T S V E R Z E I C H N I S RECHTSGRUNDLAGEN 1. ANLASS FÜR DIE AUFSTELLUNG DES BEBAUUNGSPLANES 1.1 Flächennutzungsplan 2. PLANUNGSRECHTLICHE GRUNDLAGEN 2.1 Vorhabensträger 2.2 Stadt Lichtenfels 2.3 Planungs- und Verfahrensstand 3. ZIEL DER PLANUNG 4. ABGRENZUNG UND BESCHREIBUNG DES PLANUNGSGEBIETES 4.1 Beschreibung des Gebietes 4.2 Räumlicher Geltungsbereich 4.3 Baugrund 4.4 Denkmalschutz 4.5 Schutzgebiete und schützenswerte Landschaftsteile 4.6 Entwicklung aus dem Flächennutzungsplan 4.7 Immissionsschutz 5. BESCHAFFENHEIT DES PLANUNGSGEBIETES 5.1 Topographie 5.2 Bodenbeschaffenheit 6. BODENORDNENDE -

Festsitzung Zur Bürgermedaillenverleihung
Jahrgang 35 Mittwoch, den 10. September 2014 Nummer 9 Festsitzung zur Bürgermedaillenverleihung Zusammen mit den Ehrengästen stellten sich die sechs neuen Marktleugaster Bürgermedaillen- träger der Kamera. Unser Bild zeigt (von links) Franz Gareis, Reinhold und Renate Scheunert, Irene Daig, Marianne und Walter Stanka, Rita Uome, 2. Bürgermeister Reiner Meisel, Bürgermeister Franz Uome, Landrat Klaus Peter Söllner, Kornelia und Norbert Volk, Landtagsabgeordneten Martin Schöffel, Susanne und Owald Purucker sowie Landtagsvizepräsidentin Inge Aures. Mitteilungsblatt Marktleugast und Grafengehaig - 2 - Nr. 9/14 25-jährige Gemeindepartnerschaft Festsitzung zur Bürgermedaillenverleihung Oswald Purucker, Franz Uome und Norbert Volk wurden mit der Goldenen Bürgermedaille ausgezeichnet Marianne Stanka, Franz Gareis und Reinold Scheunert bekamen die Silberne Bürgermedaille Gleich sechs Personen zeichnete der Marktgemeinderat zog 1962 nach Mannsflur in den neu gebauten Bungalow. Er Marktleugast in seiner Festsitzung am Sonntagmorgen, 31.8. besuchte die Grund- und Hauptschule. 1968 wechselte er in im Bürgersaal mit Bürgermedaillen aus. Oswald Purucker, die Realschule nach Kulmbach, die 1972 mit der mittleren Franz Uome und Norbert Volk wurden mit der Goldenen aus- Reife abschloss. Es folgte die Ausbildung zum Industriekauf- gezeichnet, Marianne Stanka, Franz Gareis und Reinhold mann bei der Firma WABAC in Kulmbach. Von 1985 bis 2002 Scheunert empfingen die Silberne Bürgermedaille. „Ihr Tun war er als Büroleiter bei der Fahnenfabrik Meinel in Marktleu- und Handeln ist wahrer Bürgersinn. Alle setzten sich ihr Leben gast und war dann bis 2013 bei der Sparkasse Kulmbach- lang selbstlos für ihre Mitmenschen und Heimatgemeinde Kronach tätig, zuletzt als Leiter der Geschäftsstelle in Press- ein. Hier und heute wollen wir Ihnen dafür danken, dass sie eck. 1976 heirate er seine Rita, die Ehe war mit zwei Kindern stets eigene Interessen hintan stellten“, betonte Bürgermeister gesegnet. -
Alte Schätze Neu Entdecken Bayreuth & Umgebung
Markgrafenkirchen entdecken. Alte Schätze neu entdecken Bayreuth & Umgebung Gräfenberg & Umgebung 26 Sonneberg 13 Kulmbach, Thurnau & 28 Umgebung Kronach, Kulmbach & Umgebung Ludwigsstadt & B85 Umgebung Hof & Umgebung B173 53 Selb, Wunsiedel & 41 Umgebung 46 44 B303 54 Lichtenfels 57 29 32 51 19 25 1 49 37 10 8 A 70 B85 11 58 2-7 14 B22 34 33 Bamberg 16 12 27 23 36 A 9 15 B2 24 18 17 40 Nürnberg Nürnberg Nürnberg Dresden Leipzig Leipzig / Berlin Leipzig A 72 50 9 52 20 22 48 42 21 31 45 A 9 39 35 B289 47 30 56 43 A 93 59 1 B303 Weiden/Regensburg 55 B22 38 Weiden B85 Dreifaltigkeitskirche 1 Bad Berneck Die Kurstadt zu Füßen Kirchenring 37 95460 Bad Berneck www.bad-berneck-evangelisch.de täglich 9 bis 17 Uhr Apr bis Okt bis 19 Uhr DB Bayreuth Hbf ZOH Bayreuth Bus 330 Fußweg ca. 3 Min. Ordenskirche 2 Bayreuth Die Fürstin der Markgrafenkirchen St. Georgen 50 95448 Bayreuth www.ordenskirche.de täglich 9 bis 16 Uhr Apr bis Okt bis 18 Uhr DB Bayreuth Hbf Fußweg ca. 12 Min. Pfarrkirche 3 St. Johannis Bayreuth Schmuckstück an Wilhelmines Eremitage Altentrebgastplatz 4 95448 Bayreuth www.stjohannis-bayreuth.de täglich 9 bis 16 Uhr Apr bis Okt bis 18 Uhr DB Bayreuth Hbf ZOH Bus 302, 302 Ri St. Johannis, Hst Ochsenhut Bayreuth & Umgebung Schlosskirche 4 Unsere liebe Frau Bay- reuth Wilhelmines Erbe Schlossberglein 1 95444 Bayreuth www.schlosskirche-bayreuth.kirche-bamberg.de täglich 7.30 bis 16 Uhr Apr bis Okt bis 19 Uhr DB Bayreuth Hbf Fußweg ca. -

Blätter Zur Flora Nordbayerns
Blätter zur Flora Nordbayerns Nr. 2 (Juli 2005) Inhalt in Stichworten Vorbemerkungen ·················································································· 1 Zur Diskussion gestellt: Darstellungsweisen, Naturräume, Abkürzungen ·································· 2 Über Hohlzähne (Galeopsis) am Westrand der Böhmischen Masse ··· 17 Galeopsis in der „Ergänzungsflora von Nordostbayern“ ······················ 42 Geplante Untersuchungen für 2005 und Folgejahre ··························· 45 Myriophyllum alterniflorum ···································································· 45 Avena-Sippen ················································································· 46 Für Nordostbayern einschlägige floristische Arbeiten ························· 47 Calystegia sepium agg. ··································································· 47 Euphorbia virgata und E. x pseudovirgata ······································ 47 Senecio velenovskyi ·············································································· 48 Pilularia globulifera ················································································· 49 Plantago coronopus ··············································································· 50 Sedum oppositifolium ············································································ 50 Kapitel “Botanique” (Camille de Tournon) ······································· 51 Potamogeton berchtoldii und Potamogeton pusillus ······················· 52 1 Vorbemerkungen Die Nr. 1 dieser -

Spielberichte FC1 2010-2011
Montag, 30. Mai 2011 SSV Kasendorf II : FC Neuenmarkt 3:1 (2:0) Tore: 1:0 Krüger (18.); 2:0 und 3:0 Wondra (20. und 52.); 3:1 Wesner (74.) Schiedsrichter: Fröba (Hirschfeld) Zuschauer: 40 Der FC spielte mit: Handlass, A.Dogru, Werner, Grieshammer, Wesner, Schröder, Geyer, Held, Promeuschel (25.Warzecha), Harttig (80.Horter), Kimmich Die Einheimischen übernahmen von Anfang an das Kommando. Nach einer Flanke von Hofmann köpfte Krüger zur frühen Führung ein. Keine zwei Minuten später besorgte Wenig nach schönem Zusammenspiel mit Morck das 2:0. Neuenmarkt blieb mit seiner Ersatzgeschwächten Mannschaft weit hinter den Erwartungen zurück. Nach dem Seitenwechsel hatte Kimmich den Anschlusstreffer für die Gäste auf dem Fuß, verzog aber allein vor dem Kasendorfer Keeper. Kurz dannach machte Wondra mit einem Traumtor alles klar. In der Folge nahm der SSV das Tempo aus dem Spiel und erlaubte dem FC einige gute Offensivszenen. Doch mehr als der Ehrentreffer durch Wesner gelang den Gästen nicht. Donnerstag, 26. Mai 2011 FC Neuenmarkt – FC Kirchleus 2:2 (0:1) Tore: 0:1 Passing (27.); 0:2 Lerner (51.); 1:2 Täffner (77.) 2:2 A. Dogru (88. ) Schiedsrichter: Bärwald (Hof) Zuschauer: 120 der FC spielte mit: Hahn, O.Dogru, Grieshammer (Woithe), Düthorn, Held, Lerner, Schröder (Wesner), Promeuschel, Täffner, Kunz, Kimmich (A.Dogru) Gewitterunterbrechung und zwei Roten Karten in der Nachspielzeit: In dieser Partie war alles geboten. Kirchleus stellte seine Auswärtsstärke unter Beweis und fuhr kluge Konter. Neuenmarkt versuchte, die Initiative zu ergreifen, und wäre beinahe in Front gegangen, als Kimmich den Pfosten traf. Nach dem 0:2 haben die Gastgeber auf bedingungslose Offensive gesetzt und wurden mit dem Remis belohnt. -

U07 G-Junioren Herbstrunde
U07 G-Junioren Herbstrunde 2.Spieltag Samstag 30.09.17 Uhrzeit: 10:00 Uhr Spielort: Sportanlage Kasendorf Erlengrund 18 95359 Kasendorf Teilnehmenden Mannschaften: SSV Kasendorf SG Rugendorf/Losau TSV Ködnitz TSV Kulmbach JFC Thurnauer Land Uhrzeit Heim - Gast Ergebnis 10:00 SSV Kasendorf - SG Rugendorf/Losau : 10:12 TSV Ködnitz - TSV Kulmbach : 10:24 SSV Kasendorf - JFC Thurnauer Land : 10:36 SG Rugendorf/Losau - TSV Ködnitz : 10:48 JFC Thurnauer Land - TSV Kulmbach : 11:00 TSV Ködnitz - SSV Kasendorf : 11:12 SG Rugendorf/Losau - JFC Thurnauer Land : 11:24 TSV Kulmbach - SSV Kasendorf : 11:36 JFC Thurnauer Land - TSV Ködnitz : 11:48 TSV Kulmbach - SG Rugendorf/Losau : U07 G-Junioren Herbstrunde 2.Spieltag Samstag 30.09.17 Uhrzeit: 10:00 Uhr Spielort: Sportanlage Lanzendorf Am Main 95502 Himmelkron-Lanzendorf Teilnehmenden Mannschaften: SV Lanzendorf SV Ludwigschorgast (SG) SV Röhrenhof VfR Katschenreuth TSC Mainleus Uhrzeit Heim - Gast Ergebnis 10:00 SV Lanzendorf - SV Ludwigschorgast : 10:12 (SG) SV Röhrenhof - VfR Katschenreuth : 10:24 SV Lanzendorf - TSC Mainleus : 10:36 SV Ludwigschorgast - (SG) SV Röhrenhof : 10:48 TSC Mainleus - VfR Katschenreuth : 11:00 (SG) SV Röhrenhof - SV Lanzendorf : 11:12 SV Ludwigschorgast - TSC Mainleus : 11:24 VfR Katschenreuth - SV Lanzendorf : 11:36 TSC Mainleus - (SG) SV Röhrenhof : 11:48 VfR Katschenreuth - SV Ludwigschorgast : U07 G-Junioren Herbstrunde 2.Spieltag Samstag 30.09.17 Uhrzeit: 10:00 Uhr Spielort: Sportanlage Bayreuth (Hartplatz möglich) Hermann-Löns-Straße 95447 Bayreuth-Glocke Teilnehmenden Mannschaften: BSC Saas Bayreuth (SG) SC Hummeltal SpVgg Oberfranken Bayreuth 2 TSV 07 St. Johannis Bayreuth Uhrzeit Heim - Gast Ergebnis 10:00 BSC Saas Bayreuth - (SG) SC Hummeltal : 10:15 SpVgg Oberfranken - TSV 07 St. -

TSV Trebgast 2 15:00 Uhr: SSV Peesten - TSV Trebgast Begrüßung Begrüßung
Schäckheftla Das offizielle Stadionblatt des SSV Peesten Saison 2017-2018 2. Ausgabe Sonntag 03.09.2017: 13:00 Uhr: SSV Peesten 2 - TSV Trebgast 2 15:00 Uhr: SSV Peesten - TSV Trebgast Begrüßung Begrüßung Liebe Sportfreunde, zu den heutigen Heimspielen begrüßen wir euch im Namen des SSV Peesten recht herzlich. Ein besonderer Gruß gilt dabei unseren Gästen aus Trebgast mit ihren Aktiven, Betreueren und Anhängern, sowie auch den eingeteilten Schiedsrichtern. Fünf Spiele - Fünf Niederlagen - Null Punkte - Tabellenletzter! Das ist die bittere Realität unserer Ersten vor dem heutigen Heimspiel gegen den TSV Trebgast, der mit zwei Punkten auch nicht gerade gut in die Saison gestartet ist. Zwar war die Leistung im Derby in Kasendorf angesichts der personell an- gespannten Lage in Ordnung, doch letztendlich nicht ausreichend um zu punkten. Dafür lief gerade in der Offensive einfach zu wenig zusammen und so musste man sich nach zwei höchst unglücklichen Gegentreffer mit 0:2 geschlagen geben. Heute gegen Trebgast wäre ein Sieg also enorm wichtig, erstens um endlich die ersten Punkte einzufahren und zweitens um die Hoffnung weiterhin auf- recht zu erhalten. Unsere Reserve holte bisher vier Punkte aus drei Spielen (Ergebnis gegen Thurnau lag bei Redaktionsschluss noch nicht vor) und hat heute gegen den TSV Trebgast 2 die Möglichkeit, den zweiten Saisonsieg einzufahren und die aufsteigende Form zu bestätigen. In diesem Sinne... Auf geht‘s Peesten, Kämpfen und Siegen!!! Die nächsten Spiele des SSV: 1. Mannschaft - Kreisklasse 4 Samstag, 09.09. um 16:00 Uhr, auswärts, VfR Katschenreuth 2 2. Mannschaft – B-Klasse 5 Samstag, 09.09. um 14:00 Uhr, auswärts, VfR Katschenreuth 3 Teamvergleich 1.