DOCSLIB.ORG

A New Dynamical Core of the Global Environmental Multiscale (GEM) Model with a Height-Based Terrain-Following Vertical Coordinate

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A New Dynamical Core of the Global Environmental Multiscale (GEM) Model with a Height-Based Terrain-Following Vertical Coordinate JULY 2019 H U S A I N E T A L . 2555 A New Dynamical Core of the Global Environmental Multiscale (GEM) Model with a Height-Based Terrain-Following Vertical Coordinate SYED ZAHID HUSAIN,CLAUDE GIRARD, AND ABDESSAMAD QADDOURI Atmospheric Numerical Prediction Research Section, Meteorological Research Division, Environment and Climate Change Canada, Dorval, Quebec, Canada ANDRÉ PLANTE Canadian Meteorological Centre, Environment and Climate Change Canada, Dorval, Quebec, Canada (Manuscript received 20 December 2018, in final form 7 May 2019) ABSTRACT A new dynamical core of Environment and Climate Change Canada’s Global Environmental Multiscale (GEM) atmospheric model is presented. Unlike the existing log-hydrostatic-pressure-type terrain- following vertical coordinate, the proposed core adopts a height-based approach. The move to a height- based vertical coordinate is motivated by its potential for improving model stability over steep terrain, which is expected to become more prevalent with the increasing demand for very high-resolution forecasting systems. A dynamical core with height-based vertical coordinate generally requires an it- erative solution approach. In addition to a three-dimensional iterative solver, a simplified approach has been devised allowing the use of a direct solver for the new dynamical core that separates a three- dimensional elliptic boundary value problem into a set of two-dimensional independent Helmholtz problems. The issue of dynamics–physics coupling has also been studied, and incorporating the physics tendencies within the discretized dynamical equations is found to be the most acceptable approach for the height-based vertical coordinate. The new dynamical core is evaluated using numerical experiments that include two-dimensional nonhydrostatic theoretical cases as well as 25-km resolution global fore- casts. For a wide range of horizontal grid resolutions—from a few meters to up to 25 km—the results from the direct solution approach are found to be equivalent to the iterative approach for the new dynamical core. Furthermore, results from the different numerical experiments confirm that the new height-based dynamical core is equivalent to the existing pressure-based core in terms of solution accuracy. 1. Introduction 2014). The existing pressure-type coordinate system then permits the use of a direct solver for the discretized The dynamical core of the Global Environmental Mul- EBV problem to resolve the dynamical component of tiscale (GEM) model, used operationally by Environ- the flow. The direct solver starts by separating the EBV ment and Climate Change Canada (ECCC) for numerical problem vertically in terms of the vertical eigenvec- weather prediction (NWP), employs a log-hydrostatic- tors of the part of the coefficient matrix that only in- pressure-type terrain-following vertical coordinate. The cludes the discretized difference and average operators system of nonlinear model equations is linearized in the vertical direction (Qaddouri and Lee 2010). For N around a basic state and is then reduced to an elliptic number of model vertical levels, the resulting N verti- boundary value (EBV) problem through numerical cally decoupled two-dimensional Helmholtz problems discretization and elimination of variables (Girard et al. are then separated along the longitude, leading to a system of tridiagonal problems depending only on the Denotes content that is immediately available upon publica- latitude. The tridiagonal problems are finally solved tion as open access. using LU decomposition without pivoting. Such an ap- proach is computationally more efficient than most it- Corresponding author: Syed Zahid Husain, syed.husain@ erative methods, particularly for the spatial resolutions canada.ca of the current operational NWP systems at ECCC. DOI: 10.1175/MWR-D-18-0438.1 For information regarding reuse of this content and general copyright information, consult the AMS Copyright Policy (www.ametsoc.org/ PUBSReuseLicenses). Unauthenticated | Downloaded 09/25/21 04:19 PM UTC 2556 MONTHLY WEATHER REVIEW VOLUME 147 One of the principal incentives for the adoption of has been found to lead to any meaningful stability im- the existing pressure-type vertical coordinate in GEM provement for steep orography. is the computational advantage of the direct solution Although the instability induced by steep orogra- approach that is permissible with such a coordinate. phy is often characterized as a limitation of the terrain- However, numerical experiments carried out at ECCC following nature of the vertical coordinate itself, have revealed that vertical separability, which is an Smolarkiewicz et al. (2007) were successful in re- imperative for the direct solution approach, can be- solving flow around the Pentagon with a model in- come quite restrictive for very high spatial resolutions volving height-based TFC where the maximum slope (e.g., for subkilometer horizontal grid spacing). Fur- was well above the widely acknowledged 458 threshold. thermore, the reduction of the 2D Helmholtz problems Previous experience with the Mesoscale Compress- into the 1D tridiagonal problems requires projection ible Community model at ECCC also suggests that a of right hand side (rhs) of the 2D problems along dynamical core with height-based TFC does not suf- the pertinent eigenvectors which is based on Fourier fer from similar severe orography-induced instability transformation. This necessitates transposing the (Girard et al. 2005). Apparently, a dynamical core coefficient matrix that involves global communica- with a height-based TFC can lead to improved nu- tions, and therefore, becomes inefficient for very large merical stability through better implicit treatment of number of processor cores. As a result, the direct solver the metric terms arising from the vertical coordinate is found to lose scalability with increasing number transformation through iterative solvers. More impor- of processor cores. Initial research at ECCC as well tantly, conventional numerical approximation of the as published research literature (Müller and Scheichl horizontal gradients in a TFC becomes less accurate 2014) reveal that optimized three-dimensional iterative with increasing terrain slope as well as with increasing solvers may possess better scalability in these circum- vertical resolution close to the model surface (Mahrer stances. The different limitations of the existing di- 1984). In this context, Zängl (2012) argues that the rect solver, particularly its potential lack of scalability pressure gradient term, in particular, becomes suscep- for future generations of massively parallel supercom- tible to triggering numerical instability when the height puters, therefore warrants the development of more difference between two adjacent grid points along a scalable iterative solvers at ECCC. A height-based terrain-following vertical level is much larger than the vertical coordinate is considered to be more amenable vertical grid resolution adjacent to the level. Numeri- to such iterative solvers as the metric terms originating cal approximation of the horizontal gradient terms in from the vertical coordinate transformation appear ex- theTFC,however,canbesignificantly improved fol- plicitly in the discretized EBV. lowing the approach proposed by Mahrer (1984). This Another, but more challenging, problem pertaining approach requires determination of the modified hor- to the existing GEM dynamical core is the fact that the izontal differencing stencils associated with each grid- current model exhibits strong numerical instability over point location that minimize the error in the metric steep orography. Tests conducted at ECCC have de- corrections for the terrain-following nature of the co- termined the maximum permissible terrain slope for ordinate. The existing pressure-type TFC varies with maintaining stability to be approximately 458 (Vionnet time and, therefore, would require determination of et al. 2015). This has been considered to be a limitation the pertinent gridpoint locations in the vertical for the inherent to the terrain-following coordinate (TFC) sys- modified differencing stencils at every time step. On tems (Zängl 2012). With a growing demand for very the contrary, the height-based TFC is time-invariant high-resolution operational NWP systems, steep oro- and thus would require the determination of these graphic slopes are expected to become more preva- gridpoint locations only once at the beginning of the lent in the near future. Improving model stability over time integration. Therefore, from a computational ef- steep mountains is therefore of critical importance for ficiency standpoint, a height-based TFC is more suitable the future development of subkilometer NWP systems. for implementing improved numerical approximation of A number of approaches have been investigated to im- horizontal gradients to address instabilities induced by prove numerical stability with the existing pressure-type steep orography. vertical coordinate in GEM. These include increased The aforementioned challenges associated with the off-centering in the discretized vertical momentum existing log-hydrostatic-pressure-type TFC motivated equation, a vertically variable basic state temperature the development of a new dynamical core for the GEM profile, and modifications to the nonhydrostatic contri- model that utilizes a height-based TFC. The primary butions in the linear system arising from the discretized objective of the present study is to demonstrate that, GEM formulation.
Load more

Recommended publications
  • Disability Classification System
    CLASSIFICATION SYSTEM FOR STUDENTS WITH A DISABILITY Track & Field (NB: also used for Cross Country where applicable) Current Previous Definition Classification Classification Deaf (Track & Field Events) T/F 01 HI 55db loss on the average at 500, 1000 and 2000Hz in the better Equivalent to Au2 ear Visually Impaired T/F 11 B1 From no light perception at all in either eye, up to and including the ability to perceive light; inability to recognise objects or contours in any direction and at any distance. T/F 12 B2 Ability to recognise objects up to a distance of 2 metres ie below 2/60 and/or visual field of less than five (5) degrees. T/F13 B3 Can recognise contours between 2 and 6 metres away ie 2/60- 6/60 and visual field of more than five (5) degrees and less than twenty (20) degrees. Intellectually Disabled T/F 20 ID Intellectually disabled. The athlete’s intellectual functioning is 75 or below. Limitations in two or more of the following adaptive skill areas; communication, self-care; home living, social skills, community use, self direction, health and safety, functional academics, leisure and work. They must have acquired their condition before age 18. Cerebral Palsy C2 Upper Severe to moderate quadriplegia. Upper extremity events are Wheelchair performed by pushing the wheelchair with one or two arms and the wheelchair propulsion is restricted due to poor control. Upper extremity athletes have limited control of movements, but are able to produce some semblance of throwing motion. T/F 33 C3 Wheelchair Moderate quadriplegia. Fair functional strength and moderate problems in upper extremities and torso.
    [Show full text]
  • Ifds Functional Classification System & Procedures
    IFDS FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2009 - 2012 Effective – 1 January 2009 Originally Published – March 2009 IFDS, C/o ISAF UK Ltd, Ariadne House, Town Quay, Southampton, Hampshire, SO14 2AQ, GREAT BRITAIN Tel. +44 2380 635111 Fax. +44 2380 635789 Email: [email protected] Web: www.sailing.org/disabled 1 Contents Page Introduction 5 Part A – Functional Classification System Rules for Sailors A1 General Overview and Sailor Evaluation 6 A1.1 Purpose 6 A1.2 Sailing Functions 6 A1.3 Ranking of Functional Limitations 6 A1.4 Eligibility for Competition 6 A1.5 Minimum Disability 7 A2 IFDS Class and Status 8 A2.1 Class 8 A2.2 Class Status 8 A2.3 Master List 10 A3 Classification Procedure 10 A3.0 Classification Administration Fee 10 A3.1 Personal Assistive Devices 10 A3.2 Medical Documentation 11 A3.3 Sailors’ Responsibility for Classification Evaluation 11 A3.4 Sailor Presentation for Classification Evaluation 12 A3.5 Method of Assessment 12 A3.6 Deciding the Class 14 A4 Failure to attend/Non Co-operation/Misrepresentation 16 A4.1 Sailor Failure to Attend Evaluation 16 A4.2 Non Co-operation during Evaluation 16 A4.3 International Misrepresentation of Skills and/or Abilities 17 A4.4 Consequences for Sailor Support Personnel 18 A4.5 Consequences for Teams 18 A5 Specific Rules for Boat Classes 18 A5.1 Paralympic Boat Classes 18 A5.2 Non-Paralympic Boat Classes 19 Part B – Protest and Appeals B1 Protest 20 B1.1 General Principles 20 B1.2 Class Status and Protest Opportunities 21 B1.3 Parties who may submit a Classification Protest
    [Show full text]
  • 6436 a Alco Dip Switches
    DIP Switches A DIP Switches GD Series - Page A3 GDH Series - Page A5 AD Series - Page A7 7000 Series - Page A11 7100 Series - Page A17 S Series - Page A18 MRD Series - Page A21 DRD Series - Page A23 DR Series - Page A25 A1 Catalog 1308390 Dimensions are in inches Dimensions are shown for USA: 1-800-522-6752 South America: 55-11-3611-1514 Issued 9-04 and millimeters unless otherwise reference purposes only. Canada: 1-905-470-4425 Hong Kong: 852-2735-1628 specified. Values in parentheses Specifications subject Mexico: 01-800-733-8926 Japan: 81-44-844-8013 www.tycoelectronics.com or brackets are metric equivalents. to change. C. America: 52-55-5-729-0425 UK: 44-141-810-8967 DIP Switches DIP Switch Part Number Index A ADE02 …………………A7 ADF07……………………A8 ADPA05S ………………A9 GDR02 …………………A5 ADE02S …………………A7 ADF07S …………………A8 ADPA05SA………………A9 GDR02S …………………A5 ADE02SA ………………A7 ADF07SA ………………A8 ADPA06 …………………A9 GDR04 …………………A5 ADE03 …………………A7 ADF07SAT………………A8 ADPA06S ………………A9 GDR04S …………………A5 ADE03S …………………A7 ADF07ST ………………A8 ADPA06SA………………A9 GDR06 …………………A5 ADE03SA ………………A7 ADF07STTR ……………A8 ADPA07 …………………A9 GDR06S …………………A5 ADE04 …………………A7 ADF07T …………………A8 ADPA07S ………………A9 GDR08 …………………A5 ADE04S …………………A7 ADF08……………………A8 ADPA07SA………………A9 GDR08S …………………A5 DIP Switches ADE04SA ………………A7 ADF08S …………………A8 ADPA08 …………………A9 GDR10 …………………A5 ADE05 …………………A7 ADF08SA ………………A8 ADPA08S ………………A9 GDR10S …………………A5 ADE05S …………………A7 ADF08SAT………………A8 ADPA08SA………………A9 GDS02……………………A3 ADE05SA ………………A7 ADF08ST ………………A8 ADPA09 …………………A9 GDS02NTS………………A3 ADE06 …………………A7 ADF08STTR
    [Show full text]
  • A9.880 P 1 of 15 Amendment of Attachment 2 Only Prepared By
    A9.880 P 1 of 15 Amendment of Attachment 2 only prepared by Mānoa Career Center. This replaces Administrative Procedure No. A9.880 dated January 2011. _ September 2013 Student Employment A9.880 Policies and Procedures on Student Employment 1. Purpose. To promulgate policies and procedures governing the employment of students by the University of Hawai'i to provide for a student classification and pay plan; and to establish the conditions of employment for students. 2. Applicability. The provisions of this directive apply to all campuses and affiliated agencies employing University of Hawai'i students. Campuses may establish additional procedures on student employment provided that they are in conformance with the provisions of this procedure. 3. Definitions. a. Student Assistants. Students who are employed by the University of Hawai'i or affiliate agencies while pursuing a certificate, degree or professional diploma. This employment, regardless of funding source, is a form of financial assistance enabling the students to pursue their education. Student employment is intended to provide students with an opportunity to meet their educational objective, therefore, student assistants are not regular employees of the University and are not entitled to the same fringe benefits. b. Campus Student Employment Office. That office of the campus which is responsible for the classification of student assistant positions, the finalizing of student assistant applications, and the placing of student assistants. A9.880 P 2 of 15 Individual campuses may make provisions to delegate these functions to other campus offices as may be appropriate to meet special campus needs. This office is responsible for the enforcement of these policies and is authorized to initiate necessary payroll transactions when violations persist (e.g.
    [Show full text]
  • Judicial Magistrate Court, Tiruttani Present : Thiru. V
    JUDICIAL MAGISTRATE COURT, TIRUTTANI PRESENT : THIRU. V. LOGANATHAN, B.A., L.L.B., D.No .1072/ 2021 Dated 31.12.2020 COVID19 ADVANCE SPECIAL CAUSE LIST, FOR 04.01.2021 (As per the OM. In D.No 5050/A/2020 dated 24.09.2020 of the Hon'ble Principal District Sessions Judge, Tiruvallur) S. Case No. Name of Parties Name of the counsel Date of Stage of the case No. Hearing 1. CC.25/2015 SI of Police App for prosecution 04.01.2021 Served summons K.K.Chatram P.S. and of Lw8, Lw12 & Vs V. Venkatesan Lw14 Parthasarathi 2. CC/79/2015 SI of Police App for prosecution 04.01.2021 SS of lw8 and Thiruvalangadu P.S. and lw10(I.O) Vs R. Sivaraj Surendhar and 3 others 3. CC.256/2014 SI of Police App for prosecution 04.01.2021 Served summons K.K. Chatramp P.S. and of Lw11 to Vs R. Sivaraj Lw13 Ramesh 4. CC.41/2012 SI of Police App for prosecution 04.01.2021 Served summons K.K.Chatram P.S. and of Lw1 to Lw7 Vs N. Mohanraj Murali 5. CC/204/2013 SI of Police App for prosecution 04.01.2021 For Judgement Tiruvalangadu P.S. and Vs V. Kishore reddy Sumath & 2 others 6. CC.124//2015 SI of Police App for prosecution 04.01.2021 For Judgement Tiruttani P.S. and Vs V.Reezar Nagappan 7. CC/201/2015 SI of Police App for prosecution 04.01.2021 Fresh summon Tiruttani P.S. and to lw2 lw3 and Vs Thirunavukarasu lw5 Maridoss 8.
    [Show full text]
  • Document Owner Suela Kodra Data Classification Confidential
    Document Classification: Public Statement of Applicability, Version 2.0, 4 May 2021 Legend for Reasons for Controls Selection LR: Legal Requirements,CO: Contractual Obligations,BR/BP: Business Requirements/Adopted Best Practices,RRA: Results of Risk Assessment Section Information security control Reference Applicable A5 Information security policies A5.1 Management direction for information security Information_Security_Policy; ISMS Yes A5.1.1 Policies for information security Manual; Security Concept A5.1.2 Review of the policies for information security Document_and_Policy Management Yes A6 Organization of information security A6.1 Internal organization ISMS Manual; Information_Security_Policy; Job Yes A6.1.1 Information security roles and responsibilities descriptions ISMS Manual; Information_Security_Policy; Yes A6.1.2 Segregation of duties Access_Control_Policy Computer_Security_Incident_Respon Yes A6.1.3 Contact with authorities se_Plan (Annex II) Computer_Security_Incident_Respon Yes A6.1.4 Contact with special interest groups se_Plan (Annex II) Information Security Risk Management Policy; Software Yes A6.1.5 Information security in project management Development Process A6.2 Mobile devices and teleworking A6.2.1 Mobile device policy Mobile_Device_Policy Yes A6.2.2 Teleworking Teleworking_Policy Yes A7 Human resource security A7.1 Prior to employment A7.1.1 Screening On_Off Boarding Checkliste Yes A7.1.2 Terms and conditions of employment Safety io Arbeitsvertrag_AT Yes A7.2 During employment Information_Security_Policy; ISMS Yes
    [Show full text]
  • US SAILING FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2013—2016 Effective—1 January 2013
    [Type text ] [Type text ] [Type text ] US SAILING FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2013—2016 Effective—1 January 2013 Originally Published—May 2013 US Sailing Member of the PO Box 1260 15 Maritime Drive Portsmouth, RI 02871-0907 Phone: 1-401-683-0800 / Toll free: 1-800-USSAIL - (1-800-877-2451) Fax: 401-683-0840 E-Mail: [email protected] International Paralympic Committee Roger H S trube, MD – A pril 20 13 1 ROGE R H STRUBE, MD – APRIL 2013 [Type text ] [Type text ] [Type text ] Contents Introduction .................................................................................................................................................... 6 Appendix to Introduction – Glossary of Medical Terminology .......................................................................... 7 Joint Movement Definitions: ........................................................................................................................... 7 Neck ........................................................................................................................................................ 7 Shoulder .................................................................................................................................................. 7 Elbow ...................................................................................................................................................... 7 Wrist ......................................................................................................................................................
    [Show full text]
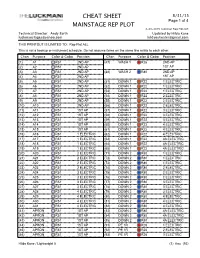
  • 8-28-2015 Luckman Rep Plot.Lw5 Technical Director: Andy Barth Updated by Hilda Kane [email protected] [email protected]
    CHEAT SHEET 8/31/15 Page 1 of 4 MAINSTAGE REP PLOT 8-28-2015 Luckman Rep Plot.lw5 Technical Director: Andy Barth Updated by Hilda Kane [email protected] [email protected] THIS PRINTOUT IS LIMITED TO: Rep Plot ALL This is not a hookup or instrument schedule. Do not assume items on the same line relate to each other. Chan Purpose Color & Gobo Position Chan Purpose Color & Gobo Position (1) A1 R51 2ND AP (47) WASH 1 R26 2ND AP (2) A2 R51 2ND AP 1ST AP (3) A3 R51 2ND AP (48) WASH 2 R80 2ND AP (4) A4 R51 2ND AP 1ST AP (5) A5 R51 2ND AP (51) DOWN 1 R22 1 ELECTRIC (6) A6 R51 2ND AP (52) DOWN 1 R22 1 ELECTRIC (7) A7 R51 2ND AP (53) DOWN 1 R22 1 ELECTRIC (8) A8 R51 2ND AP (54) DOWN 1 R22 2 ELECTRIC (9) A9 R51 2ND AP (55) DOWN 1 R22 2 ELECTRIC (10) A10 R51 2ND AP (56) DOWN 1 R22 2 ELECTRIC (11) A11 R51 1ST AP (57) DOWN 1 R22 3 ELECTRIC (12) A12 R51 1ST AP (58) DOWN 1 R22 3 ELECTRIC (13) A13 R51 1ST AP (59) DOWN 1 R22 3 ELECTRIC (14) A14 R51 1ST AP (60) DOWN 1 R22 4 ELECTRIC (15) A15 R51 1ST AP (61) DOWN 1 R22 4 ELECTRIC (16) A16 R51 1 ELECTRIC (62) DOWN 1 R22 4 ELECTRIC (17) A17 R51 1 ELECTRIC (63) DOWN 1 R22 4A ELECTRIC (18) A18 R51 1 ELECTRIC (64) DOWN 1 R22 4A ELECTRIC (19) A19 R51 1 ELECTRIC (65) DOWN 1 R22 4A ELECTRIC (20) A20 R51 2 ELECTRIC (71) DOWN 2 R80 1 ELECTRIC (21) A21 R51 2 ELECTRIC (72) DOWN 2 R80 1 ELECTRIC (22) A22 R51 2 ELECTRIC (73) DOWN 2 R80 1 ELECTRIC (23) A23 R51 2 ELECTRIC (74) DOWN 2 R80 2 ELECTRIC (24) A24 R51 3 ELECTRIC (75) DOWN 2 R80 2 ELECTRIC (25) A25 R51 3 ELECTRIC (76) DOWN 2 R80 2 ELECTRIC (26) A26 R51 3 ELECTRIC (77) DOWN 2 R80 3 ELECTRIC (27) A27 R51 3 ELECTRIC (78) DOWN 2 R80 3 ELECTRIC (28) A28 R51 4 ELECTRIC (79) DOWN 2 R80 3 ELECTRIC (29) A29 R51 4 ELECTRIC (80) DOWN 2 R80 4 ELECTRIC (30) A30 R51 4 ELECTRIC (81) DOWN 2 R80 4 ELECTRIC (31) A31 R51 4 ELECTRIC (82) DOWN 2 R80 4 ELECTRIC (41) APRON R51 1ST AP (83) DOWN 2 R80 4A ELECTRIC (42) APRON ..
    [Show full text]
  • USCIS Employment Authorization Documents
    USCIS Employment Authorization Documents March 19, 2018 Fiscal Year 2017 Report to Congress U.S. Citizenship and Immigration Services Message from U.S. Citizenship and Immigration Services March 19, 2018 I am pleased to present the following report, “USCIS Employment Authorization Documents,” which has been prepared by U.S. Citizenship and Immigration Services (USCIS). This report was compiled pursuant to language set forth in Senate Report 114-264 accompanying the Fiscal Year (FY) 2017 Department of Homeland Security Appropriations Act (P.L. 115-31). Pursuant to congressional requirements, this report is being provided to the following Members of Congress: The Honorable John R. Carter Chairman, House Appropriations Subcommittee on Homeland Security The Honorable Lucille Roybal-Allard Ranking Member, House Appropriations Subcommittee on Homeland Security The Honorable John Boozman Chairman, Senate Appropriations Subcommittee on Homeland Security The Honorable Jon Tester Ranking Member, Senate Appropriations Subcommittee on Homeland Security I am pleased to respond to any questions you may have. Please do not hesitate to contact me at (202) 272-1000 or the Department’s Acting Chief Financial Officer, Stacy Marcott, at (202) 447-5751. Sincerely, L. Francis Cissna Director U.S. Citizenship and Immigration Services i Executive Summary This report provides the information requested by the Senate Appropriations Committee regarding the number of employment authorization documents (EAD) issued annually from FY 2012 through FY 2015, the validity period of those EADs, and the policies governing validity periods of EADs. As requested, the report provides details on the number and type of EAD approvals by USCIS. From FYs 2012–2015, USCIS approved more than 6 million EADs in multiple categories.
    [Show full text]
  • Hitop®-Therapy Chart
    gbo-HiToP-Therapietafel-e 01.02.2007 18:09 Uhr Seite 1 Your competent ® and innovative partner HiToP -Therapy Chart in the field of physical therapy. 123456789 Excerpt from the indication menu Treatment of the whole body A1 Gynecology and urology Adnexitis, chronic A2 + A3 Dysmenorrhea A2 + A3 Obstipation, atonic A4 + A5 Obstipation, spastic A4 + A5 Postoperative intestinal atonia A4 + A5 Pains caused by intra-uterine device A2 + A3 Ear, nose and throat science Otitis media chronica A6 Tinnitus A6 Internal medicine and angiology Adiposity, fatness A7 A Occlusive arterial diseases A1 Bronchial asthma D4 + D5 Diabetic angiopathies A1 Endangiitis obliterans A8 Haematoma in the area of the calf B1 Heart complaints, functional B2 Migraine (treatment in intervals) B3 Obstipation, atonic A4 + A5 Obstipation, spastic A4 + A5 RAYNAUD’s syndrome B4 Neurology Amyotrophic lateral sclerosis A1 Atypical prosopalgia B5, four button electrode Facial-nerve paresis B5, four button electrode Migraine (treatment in intervals) B3, four button electrode Polyneuropathy A1 Shoulder pains in case of hemiplegia B6 + B7 Tension headache B3, four button electrode B Trigeminal neuralgia B5, four button electrode Vasomotor headache B3, four button electrode Orthopedics, surgery, sports medicine Achillodynia, calcaneal apophysitis C8 Carpus arthrosis C7 Arthrosis of knee-joint D2 + D3 Arthrosis of shoulder B6 + B7 Arthrosis of ankle joint C9 BAKER’s cysts C6 Prepatellar bursitis C6 Patellar chondromalacia C6 Patellar chondropathy C6 Coxarthrosis, arthrosis of hip joint
    [Show full text]
  • Specification for Welding Shielding Gases
    ANSI/AWS A5.32/A5.32M-97 An American National Standard Specification for Welding Shielding Gases Key Words— Argon, carbon dioxide, helium, ANSI/AWS A5.32/A5.32M-97 hydrogen, nitrogen, oxygen, shielding An American National Standard gases, welding gases Approved by American National Standards Institute December 8, 1997 Specification for Welding Shielding Gases Prepared by AWS Committee on Filler Metals Under the Direction of AWS Technical Activities Committee Approved by AWS Board of Directors Abstract This specification for welding shielding gases specifies minimum requirements for the composition and purity of the most popular single-component shielding gases. Classification designators for both single and multicomponent gases are introduced. Other topics include testing procedures, package marking, and general application guidelines. This specification makes use of both U.S. Customary Units and the International System of Units (SI). Since these are not equivalent, each system must be used independently of the other. 550 N.W. LeJeune Road, Miami, Florida 33126 Table of Contents Page No. Personnel.................................................................................................................................................................... iii Foreword ................................................................................................................................................................... v List of Tables ..............................................................................................................................................................vii
    [Show full text]
  • Markerless Measurement and Evaluation of General Movements in Infants
    www.nature.com/scientificreports OPEN Markerless Measurement and Evaluation of General Movements in Infants Toshio Tsuji1*, Shota Nakashima1, Hideaki Hayashi2, Zu Soh1, Akira Furui 1, Taro Shibanoki3, Keisuke Shima4 & Koji Shimatani5 General movements (GMs), a type of spontaneous movement, have been used for the early diagnosis of infant disorders. In clinical practice, GMs are visually assessed by qualifed licensees; however, this presents a difculty in terms of quantitative evaluation. Various measurement systems for the quantitative evaluation of GMs track target markers attached to infants; however, these markers may disturb infants’ spontaneous movements. This paper proposes a markerless movement measurement and evaluation system for GMs in infants. The proposed system calculates 25 indices related to GMs, including the magnitude and rhythm of movements, by video analysis, that is, by calculating background subtractions and frame diferences. Movement classifcation is performed based on the clinical defnition of GMs by using an artifcial neural network with a stochastic structure. This supports the assessment of GMs and early diagnoses of disabilities in infants. In a series of experiments, the proposed system is applied to movement evaluation and classifcation in full-term infants and low- birth-weight infants. The experimental results confrm that the average agreement between four GMs classifed by the proposed system and those identifed by a licensee reaches up to 83.1 ± 1.84%. In addition, the classifcation accuracy of normal and abnormal movements reaches 90.2 ± 0.94%. UNICEF reported in “Te State of the World’s Children 2016” that approximately 10% of newborn babies in Japan have a low birth weight (LBW), and this percentage is expected to increase in the near future1.
    [Show full text]