DOCSLIB.ORG

An Electron Impact Investigation of the Fluorinated Methanes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
An Electron Impact Investigation of the Fluorinated Methanes AN ELECTRON IMPACT INVESTIGATION OF THE FLUORINATED METHANES DISSERTATION Presented In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of the Ohio State University By EDWIN HENRY LOUGHER, B.S. The Ohio State University 1952 Approved by Advisor ACKNOWLEDGEMENT I wish to express my appreciation to Dr. E. N. Lassettre for his assistance during the course of this investigation. His interest and grasp of the problems involved were a principal factor in the completion of the work. I should like to thank Dr. A. L. Henne for valuable advice and for some of the materials used in this investigation. I wish to thank Dr. A. B. Garrett, the Chemistry Department, and the Ohio State Research Foundation for the assistantships which enabled me to carry this work to completion. Finally, I wish to thank my wife for her continued encouragement and for typing this dissertation. 8 0 0 4 6 1 TABLE OF CONTENTS Page Introduction 1 I. History and Theory 2 A. History of Electron Impact Work 2 B. General Theory of Electron Impact Spectra 3 C. Localization of Valence Electrons 8 (1) The Concept of Localization 8 (2) Electron Impact Spectra of Saturated and Unsaturated Hydrocarbons 10 (3) Localized and Non Localized Molecular Orbitals 13 (4) Localized and Non Localized Molecular Orbitals in Excitation Processes 21 D. Choice of Compounds 23 II. The Electron Spectrometer 24 A. General Description 24 B. Modification of the Apparatus 32 C. Operational Procedure 35 III. Experimental Work 39 A. Materials 39 B. Graphs of Observed Spectra 43 C. Table of Excitation Potentials 53 11 Page. IV. Discussion of Results 54 A. Decomposition by the Emitter 54 B. Discussion of the Spectra 56 C. General Significance 58 D. Theory of Energy States and Selection Rules 62 (1) Bonding Orbitals in the Ground State 63 (2) Excited States ( <5~~ System) 75 (3) Unshared Electron Pairs 85 (4) Interpretation of the Spectra 87 Summary 90 Appendix 91 A. Analyzer Correction Formula 91 B. Electrometer Bridge Calibration Factors 91 C. Tables of Data 92 Bibliography 120 Autobiography 122 H i ILLUSTRATIONS Flcure Pace 1 The Electron Spectrometer 25 2 Energy Spread In Direct Beam 33 3 Infrared Spectrum of Methyl Fluoride 42 4 Methane Spectra 45 5 Monofluoromethane Spectra 46 6 Difluoromethane Spectra 47 7 Trifluoromethane Spectra 48 8 Tetrafluoromethane Spectra 49 9 Comparison of Spectra of Fluorinated Methanes 50 10 Vinyl Fluoride Spectrum 51 11 Vacuum Spectra 52 12 Energy Levels and Selection Rules 79 iv TABLES Xflble Z&ge 1 Excitation Potentials 53 2 Character Table for CH^ 66 3 Irreducible Representations for CH4 (T^) 68 4 Irreducible Representations for CH^F (C^) 68 5 Irreducible Representations for CHgFg (Cgv) 69 6 Irreducible Representations for CHFg CC«3 V ) 69 7 Irreducible Representations for CF4 (T,^) 70 8 Matrices of Coefficients in Variation Equations 73 9 Ground State Energy Levels 74 10 S election Rules 78 v INTRODUCTION This Investigation had two purposes. One was to investigate the electron impact spectra of methane and its fluorine derivatives. The other, and princi­ pal, purpose was to determine whether the valence electrons in a molecule should be considered as localized, that is, associated with specific bonds, or as non-locallzed and as-sociated with the molecule as a whole* Following this Introduction is a history of electron impact work and of the previous work which has indicated the need for this Investigation. Also Included in this section are a review of the general theory of electon impact work and a com­ parison of the methods of localized and non-localized molecular orbitals. The criteria which led to the choice, of methane and its fluorine derivatives for the purpose of this investigation are discussed. Following this section are descriptions of the elec­ tron spectrometer, the experimental procedure, and the materials used. The results are presented as energy spectra, and their significance with respect to localization of electrons is discussed. 2 I HISTORY AND THEORY A. Hlatory of Electron Impact Work In the past, numerous systems have been investi­ gated by means of electron Impact, The early -work was confined to the determination of critical potentials of atoms and molecules. This work is reviewed by Arnot (1) and Darrow (2). More recently, Investigations of energy spectra have been carried out, using some sort of analyzer which separates the electrons of various energies. Harnwell (3) and, Dymond and Watson (4) were some of the first workers In this field. Hughes and RoJansky (5) developed the theory of the 127° electrostatic analyzer which was sub­ sequently used by Hughes and McMIllen (6) for various Investigations. B . General Theory of Electron Impact Spectra Electron Impact spectra are obtained by passing a monoenergetic electron beam through a gas at low pressure. Electrons which undergo Inelastic collisions with molecules or atoms of the gas, thereby exciting the molecules or atoms to higher quantum states, lose some of their energy. The energy losses are, of course, quantized. The electrons of different energies are then separated by means of some sort of velocity analyzer and the relative numbers at the various energies are measured. A plot of the collected current against the electron energy thien gives a spectrum of the gas under Investigation. The spectra are sometimes unresolved over the entire spectral region, due to the thermal energy spead In the electron beam, finite slit widths, and departure from perfect focusing In the velocity analyzer. Spectra obtained for atomic gases exhibit sharper peaks and deeper valleys than those for molecular gases, since molecular spectra have vibrational and rotational fine structure which Is not resolved by the spectrometer. The gas pressures used in the scattering chamberare low - of the order of 10_4: to 10*“^ millimeters of mercury. At such pressures, the mean free path for electrons is great enough so that the effect of multiple collisions, 4 that Is successive excitations of the same atom or mole­ cule, or successive collisions by a single electron, may be neglected. Electron Impact spectra extend to the far ultraviolet region of optical spectra. The selection rules for tran­ sition appear to be the same for electron energies above about 180 electron volts. With beams of lower energy, optically forbidden transitions may occur. A theoretical basis for this follows. Consider an electron in Inelastic collision with a molecule, atom, or Ion. Let the initial energy of the electron be = | **12 an<a- ^ e final energy be Eg - £ Pg2 , where P^ and Pg are the Initial and final momenta in atomic units. If the energy lost by the electron in exciting the scattering particle to a higher energy state be designated as I, then, by the law of conservation of energy, p-^/s - p 22/2 = I * The square of the change in momentum, AP^, is given by A P 2 = Px2 + P 22 - S P ^ g C o s # , where i) Is the scattering angle. At small angles, that is when \9- Osd 0, AP 2 =■ (Pj_ - Pg)2. 5 Now P2 = (P!2 - 21)^ p 2 = px d - V ej.)4 * Expanding and neglecting terms of order higher than (^/g) » P 2 = P 1 U “ -2E> • Then AP = (Px - P2) - XgljT-ir • The Born approximation (7) for the scattering of high energy electron Is CTi = .*+ » where £ = % < / C cJT ' Here (jj~ = the scattering cross section for the 1—th transition, = the wave function for the ground state of the scattering particle, and ^ = the wave function for the 1— th excited state of the scattering particle. The summation Is over all the molecular electrons, and the Integration Is over the coordinates of all the molecular electrons. The symbol ]£)X represents the square of the absolute magnitude of averaged over all molecular orientations. 6 Since P I s email, we may expand the expression for In a Maclaurln series to give <2 ' £n-o ( i Ap)nC n where K l f k-Tf)" d Y AP_ and k ~ |AF( J ^ Now If and are real , <Cn ~ and ic r AP£,’( - apV-' ^ A) +■ ^'p<’ a -tZS'^-)+' Then, since A P = — I— - . 1 , T u J T t ' or, since |< is Independent of the coordinates of the molecular electrons, C = iT-tefi; V* ^ d r ; . But the matrix element of dipole moment /£= 5-/»i rfr , eo that £ = 7c - ^ - r - > But k Is a unit vector, so that If is the angle between k" and , £ . = * Now is the value of C^~ averaged over all possible molecular orientations. But the average value of the square of a direction cosine Is 1/3, so that £ ^ = k5ytA.* Now If o< - - 4 ^ ^ - 2. £ , ) and z. ( e ; - 2 +■ a <f, « v ) , . 2. then -f ^ -+- (3 -fr- { -3 1 1 For high energy electrons, the first term of this expression Is the most important. The second term does not depend upon E^, and all higher terms decrease with increasing E^. Thus, for high energy electrons, the only allowed transitions are those which are optically allowed, that Is, those for which the matrix element of dipole moment does not vanish. 8 0. Localization of Valence Electrons. (1) The Concept of Localization The concept of localization of electrons within a molecule is an Integral part of the chemical theory of valence. The concept of an electron pair bond was Introduced into the theory by G-. N. Lewis (7) and I. Langmuir (8) and strongly implies that in each bond a pair of electrons is localized in the vlclnityof the two bonded atoms. This theory has had many successes in coordinating the properties of large clases of chemical substances and was proposed primarily for this purpose. Nevertheless, in some cases its success was limited, and with the advent of a quantum mechanical theory of valence its limitation was explicitly recognized by introducing the concept of resonance.
Load more

Recommended publications
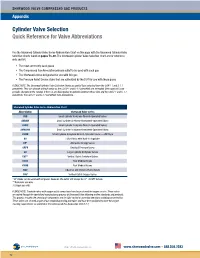
  • Cylinder Valve Selection Quick Reference for Valve Abbreviations
    SHERWOOD VALVE COMPRESSED GAS PRODUCTS Appendix Cylinder Valve Selection Quick Reference for Valve Abbreviations Use the Sherwood Cylinder Valve Series Abbreviation Chart on this page with the Sherwood Cylinder Valve Selection Charts found on pages 73–80. The Sherwood Cylinder Valve Selection Chart are for reference only and list: • The most commonly used gases • The Compressed Gas Association primary outlet to be used with each gas • The Sherwood valves designated for use with this gas • The Pressure Relief Device styles that are authorized by the DOT for use with these gases PLEASE NOTE: The Sherwood Cylinder Valve Selection Charts are partial lists extracted from the CGA V-1 and S-1.1 pamphlets. They can change without notice as the CGA V-1 and S-1.1 pamphlets are amended. Sherwood will issue periodic changes to the catalog. If there is any discrepancy or question between these lists and the CGA V-1 and S-1.1 pamphlets, the CGA V-1 and S-1.1 pamphlets take precedence. Sherwood Cylinder Valve Series Abbreviation Chart Abbreviation Sherwood Valve Series AVB Small Cylinder Acetylene Wrench-Operated Valves AVBHW Small Cylinder Acetylene Handwheel-Operated Valves AVMC Small Cylinder Acetylene Wrench-Operated Valves AVMCHW Small Cylinder Acetylene Handwheel-Operated Valves AVWB Small Cylinder Acetylene Wrench-Operated Valves — WB Style BV Hi/Lo Valves with Built-in Regulator DF* Alternative Energy Valves GRPV Residual Pressure Valves GV Large Cylinder Acetylene Valves GVT** Vertical Outlet Acetylene Valves KVAB Post Medical Valves KVMB Post Medical Valves NGV Industrial and Chrome-Plated Valves YVB† Vertical Outlet Oxygen Valves 1 * DF Valves can be used with all gases; however, the outlet will always be ⁄4"–18 NPT female.
    [Show full text]
  • Evolution of Refrigerants Mark O
    This is an open access article published under an ACS AuthorChoice License, which permits copying and redistribution of the article or any adaptations for non-commercial purposes. pubs.acs.org/jced Review (R)Evolution of Refrigerants Mark O. McLinden* and Marcia L. Huber Cite This: J. Chem. Eng. Data 2020, 65, 4176−4193 Read Online ACCESS Metrics & More Article Recommendations *sı Supporting Information ABSTRACT: As we enter the “fourth generation” of refrigerants, we consider the evolution of refrigerant molecules, the ever- changing constraints and regulations that have driven the need to consider new molecules, and the advancements in the tools and property models used to identify new molecules and design equipment using them. These separate aspects are intimately intertwined and have been in more-or-less continuous development since the earliest days of mechanical refrigeration, even if sometimes out-of-sight of the mainstream refrigeration industry. We highlight three separate, comprehensive searches for new refrigerantsin the 1920s, the 1980s, and the 2010sthat sometimes identified new molecules, but more often, validated alternatives already under consideration. A recurrent theme is that there is little that is truly new. Most of the “new” refrigerants, from R-12 in the 1930s to R- 1234yf in the early 2000s, were reported in the chemical literature decades before they were considered as refrigerants. The search for new refrigerants continued through the 1990s even as the hydrofluorocarbons (HFCs) were becoming the dominant refrigerants in commercial use. This included a return to several long-known natural refrigerants. Finally, we review the evolution of the NIST REFPROP database for the calculation of refrigerant properties.
    [Show full text]
  • "Fluorine Compounds, Organic," In: Ullmann's Encyclopedia Of
    Article No : a11_349 Fluorine Compounds, Organic GU¨ NTER SIEGEMUND, Hoechst Aktiengesellschaft, Frankfurt, Federal Republic of Germany WERNER SCHWERTFEGER, Hoechst Aktiengesellschaft, Frankfurt, Federal Republic of Germany ANDREW FEIRING, E. I. DuPont de Nemours & Co., Wilmington, Delaware, United States BRUCE SMART, E. I. DuPont de Nemours & Co., Wilmington, Delaware, United States FRED BEHR, Minnesota Mining and Manufacturing Company, St. Paul, Minnesota, United States HERWARD VOGEL, Minnesota Mining and Manufacturing Company, St. Paul, Minnesota, United States BLAINE MCKUSICK, E. I. DuPont de Nemours & Co., Wilmington, Delaware, United States 1. Introduction....................... 444 8. Fluorinated Carboxylic Acids and 2. Production Processes ................ 445 Fluorinated Alkanesulfonic Acids ...... 470 2.1. Substitution of Hydrogen............. 445 8.1. Fluorinated Carboxylic Acids ......... 470 2.2. Halogen – Fluorine Exchange ......... 446 8.1.1. Fluorinated Acetic Acids .............. 470 2.3. Synthesis from Fluorinated Synthons ... 447 8.1.2. Long-Chain Perfluorocarboxylic Acids .... 470 2.4. Addition of Hydrogen Fluoride to 8.1.3. Fluorinated Dicarboxylic Acids ......... 472 Unsaturated Bonds ................. 447 8.1.4. Tetrafluoroethylene – Perfluorovinyl Ether 2.5. Miscellaneous Methods .............. 447 Copolymers with Carboxylic Acid Groups . 472 2.6. Purification and Analysis ............. 447 8.2. Fluorinated Alkanesulfonic Acids ...... 472 3. Fluorinated Alkanes................. 448 8.2.1. Perfluoroalkanesulfonic Acids
    [Show full text]
  • THOMAS MIDGLEY, JR., and the INVENTION of CHLOROFLUOROCARBON REFRIGERANTS: IT AIN’T NECESSARILY SO Carmen J
    66 Bull. Hist. Chem., VOLUME 31, Number 2 (2006) THOMAS MIDGLEY, JR., AND THE INVENTION OF CHLOROFLUOROCARBON REFRIGERANTS: IT AIN’T NECESSARILY SO Carmen J. Giunta, Le Moyne College The 75th anniversary of the first public Critical readers are well aware description of chlorofluorocarbon (CFC) of the importance of evaluating refrigerants was observed in 2005. A sources of information. For ex- symposium at a national meeting of ample, an article in Nature at the the American Chemical Society (ACS) end of 2005 tested the accuracy on CFCs from invention to phase-out of two encyclopedias’ entries on a (1) and an article on their invention sample of topics about science and and inventor in the Chemical Educa- history of science (3). A thought- tor (2) marked the occasion. The story ful commentary published soon of CFCs—their obscure early days as afterwards raised questions on just laboratory curiosities, their commercial what should count as an error in debut as refrigerants, their expansion into assessing such articles: omissions? other applications, and the much later disagreements among generally re- discovery of their deleterious effects on liable sources (4)? Readers of his- stratospheric ozone—is a fascinating torical narratives who are neither one of science and society well worth practicing historians nor scholarly telling. That is not the purpose of this amateurs (the category to which I article, though. aspire) may find an account of a Thomas Midgley, Jr. historical research process attrac- This paper is about contradictory Courtesy Richard P. Scharchburg tive. As a starting point, consider sources, foggy memories, the propaga- Archives, Kettering University the following thumbnail summary tion of error, and other obstacles to writ- of the invention.
    [Show full text]
  • Overview of Fluorocarbons
    Three Bond Technical News Issued Dec. 20, 1989 An Overview of Fluorocarbons Introduction Currently, chlorofluorocarbons are garnering a lot of Three Bond Co,. Ltd. has been working night and day in attention around the world. Chlorofluorocarbons are used in search of alternatives to chlorofluorocarbons. In the future, many of our products and when we look at the future of products that do not contain any chlorofluorocarbons will chlorofluorocarbons in the world, and in Japan, we can replace products that now contain chlorofluorocarbons. To foresee that their use will be strictly limited or eliminated all ensure these products reach our customers as smoothly as together. possible, it is important that they have a good understanding of the issues surrounding chlorofluorocarbons. Whatever the case, Three Bond Co., Ltd. is obligated to provide our customers with products that have the same functionality as chlorofluorocarbons. Contents Introduction ................................................................................................................................................................1 1. What is a fluorocarbon? .......................................................................................................................................2 2. Properties of fluorocarbons ..................................................................................................................................2 3. Types of fluorocarbons.........................................................................................................................................2
    [Show full text]
  • Halocarbon 41, HFC-41
    SAFETY DATA SHEET Fluoromethane Issue Date: 16.01.2013 Version: 1.1 SDS No.: 000010021722 Last revised date: 19.03.2021 1/26 SECTION 1: Identification of the substance/mixture and of the company/undertaking 1.1 Product identifier Product name : Fluoromethane Other Name : R41, Halocarbon 41, HFC-41 Additional identification Chemical name: Fluoromethane Chemical formula: CH3F INDEX No. - CAS-No. 593-53-3 EC No. 209-796-6 REACH Registration No. 01-2120746661-53 1.2 Relevant identified uses of the substance or mixture and uses advised against Identified uses : Industrial and professional. Perform risk assessment prior to use. Aerosol propellant. Use as an Intermediate (transported, on-site isolated). Use for electronic component manufacture. Using gas alone or in mixtures for the calibration of analysis equipment. Uses advised against Consumer use. 1.3 Details of the supplier of the safety data sheet Supplier BOC Telephone : 0800 111 333 Priestley Road, Worsley M28 2UT Manchester E-mail: [email protected] 1.4 Emergency telephone number: 0800 111 333 SECTION 2: Hazards identification 2.1 Classification of the substance or mixture Classification according to Regulation (EC) No 1272/2008 as amended. Physical Hazards Gases under pressure Liquefied gas H280: Contains gas under pressure; may explode if heated. Flammable gas Category 1 H220: Extremely flammable gas. SDS_GB - 000010021722 SAFETY DATA SHEET Fluoromethane Issue Date: 16.01.2013 Version: 1.1 SDS No.: 000010021722 Last revised date: 19.03.2021 2/26 2.2 Label Elements Signal Word : Danger Hazard Statement(s) : H220: Extremely flammable gas. H280: Contains gas under pressure; may explode if heated.
    [Show full text]
  • Refrigerants
    Related Commercial Resources CHAPTER 29 REFRIGERANTS Refrigerant Properties .................................................................................................................. 29.1 Refrigerant Performance .............................................................................................................. 29.6 Safety ............................................................................................................................................. 29.6 Leak Detection .............................................................................................................................. 29.6 Effect on Construction Materials .................................................................................................. 29.9 EFRIGERANTS are the working fluids in refrigeration, air- cataracts, and impaired immune systems. It also can damage sensi- R conditioning, and heat-pumping systems. They absorb heat tive crops, reduce crop yields, and stress marine phytoplankton (and from one area, such as an air-conditioned space, and reject it into thus human food supplies from the oceans). In addition, exposure to another, such as outdoors, usually through evaporation and conden- UV radiation degrades plastics and wood. sation, respectively. These phase changes occur both in absorption Stratospheric ozone depletion has been linked to the presence of and mechanical vapor compression systems, but not in systems oper- chlorine and bromine in the stratosphere. Chemicals with long ating on a gas cycle using a
    [Show full text]
  • DECOMPOSITION PRODUCTS of FLUOROCARBON POLYMERS
    criteria for a recommended standard . occupational exposure to DECOMPOSITION PRODUCTS of FLUOROCARBON POLYMERS U.S. DEPARTMENT OF HEALTH, EDUCATION, AND WELFARE criteria for a recommended standard... OCCUPATIONAL EXPOSURE TO DECOMPOSITION PRODUCTS of FLUOROCARBON POLYMERS U.S. DEPARTMENT OF HEALTH, EDUCATION, AND WELFARE Public Health Service Center for Disease Control National Institute for Occupational Safety and Health September 1977 For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402 DHEW (NIOSH) Publication No. 77-193 PREFACE The Occupational Safety and Health Act of 1970 emphasizes the need for standards to protect the health and safety of workers exposed to an ever-increasing number of potential hazards at their workplace. The National Institute for Occupational Safety and Health has projected a formal system of research, with priorities determined on the basis of specified indices, to provide relevant data from which valid criteria for effective standards can be derived. Recommended standards for occupational exposure, which are the result of this work, are based on the health effects of exposure. The Secretary of Labor will weigh these recommendations along with other considerations such as feasibility and means of implementation in developing regulatory standards. It is intended to present successive reports as research and epidemiologic studies are completed and as sampling and analytical methods are developed. Criteria and standards will be reviewed periodically to ensure continuing protection of the worker. I am pleased to acknowledge the contributions to this report on the decomposition products of fluorocarbon polymers by members of the NIOSH staff and the valuable constructive comments by the Review Consultants on the Decomposition Products of Fluorocarbon Polymers and by Robert B.
    [Show full text]
  • Fluoromethane (R41) 059
    Page : 1 / 9 SAFETY DATA SHEET Revised edition no : 3 - 00 BC in accordance with REACH Date : 31 / 1 / 2014 regulation 1907/2006/EC Supersedes : 2 / 10 / 2012 Fluoromethane (R41) 059 SECTION 1. Identification of the substance/mixture and of the company/undertaking 1.1. Product identifier Trade name : Fluoromethane (R41) SDS Nr : 059 Chemical description : Fluoromethane (R41) CAS No :593-53-3 EC No :209-796-6 Index No :--- Registration-No. : Registration deadline not expired. Chemical formula : CH3F 1.2. Relevant identified uses of the substance or mixture and uses advised against Relevant identified uses : Test gas / Calibration gas. Industrial and professional. Perform risk assessment prior to use. Laboratory use. Contact supplier for more uses information. Use as refrigerant. Chemical reaction / Synthesis. 1.3. Details of the supplier of the safety data sheet Company identification : AIR LIQUIDE Deutschland GmbH Hans-Günther-Sohl-Straße 5 D-40235 Düsseldorf GERMANY Telefon: +49 (0)211 6699-0 - Fax: +49 (0)211 6699-222 E-Mail address (competent person) : [email protected] 1.4. Emergency telephone number Emergency telephone number : +49 (0)2151 398668 SECTION 2. Hazards identification 2.1. Classification of the substance or mixture Hazard Class and Category Code(s), Regulation (EC) No 1272/2008 (CLP) • Physical hazards : Flammable gases - Category 1 - Danger - (CLP : Flam. Gas 1) - H220 Gases under pressure - Liquefied gas - Warning - (CLP : Press. Gas) - H280 Classification EC 67/548 or EC 1999/45 Classification : F+; R12 Not included in Annex VI. 2.2. Label elements Labelling Regulation EC 1272/2008 (CLP) • Hazard pictograms M— M« • Hazard pictograms code : GHS02 - GHS04 • Signal words : Danger • Hazard statements : H220 - Extremely flammable gas.
    [Show full text]
  • SAFETY DATASHEET Revision Date : 06/2021
    Page : 1/10 Revised edition n° : 10.1 SAFETY DATASHEET Revision date : 06/2021 MTG059 Fluoromethane (R41) SECTION 1: Identification of the substance/mixture and of the company/undertaking 1.1. Product identifier Trade name Fluoromethane (R41) Chemical description Fluoromethane, Methyl fluoride CAS N° 593-53-3 CE N° 209-796-6 Index N° -- Registration n° 01-2120746661-53 Chemical formula CH3F 1.2. Relevant identified uses of the substance or mixture and uses advised against Relevant identified uses Industrial and professional Test gas/Calibration gas Chemical reaction / Synthesis Use as refrigerant Laboratory use Polymer production. Contact supplier for more information on uses Uses advised against Consumer use not recommended 1.3. Details of the supplier of the safety data sheet MULTIGAS Company identification Route de l’Industrie 102 CH-1564 Domdidier Phone number +41 (0) 26 676 94 94 E-mail address [email protected] 1.4. Emergency telephone numbers 145 (Toxicology Centre Zurich) or +41 (0) 44 251 51 51 +41 (0) 26 676 94 94 (Multigas) SECTION 2: Hazards identification 2.1. Classification of the substance or mixture Classification according to Regulation (EC) No. 1272/2008 [CLP] Physical hazards Flammable gases, Category 1 H220 Gases under pressure : Liquefied gas H280 Page : 2/10 Revised edition n° : 10.1 SAFETY DATASHEET Revision date : 06/2021 MTG059 Fluoromethane (R41) For the complete H-sentences texts mentioned in that chapter, refer to Section 16 2.2. Label elements Labelling according to Regulation (EC) No. 1272/2008 [CLP] Hazard pictograms GHS02 GHS04 Signal word Danger Hazard statements H220 Extremely flammable gas H280 Contains gas under pressure; may explode if heated Precautionary statements P210 Keep away from heat, hot surfaces, sparks, open flames and other ignition sources.
    [Show full text]
  • C1 and Cz FLUORINATED HYDROCARBON EFFECTS on the EXTINCTION CHARACTERISTICS of METHANE VS
    Presented at the Halon Opiions Technical Working Conference, Albuquerque, NM,May 6-8, 1997 C1 AND Cz FLUORINATED HYDROCARBON EFFECTS ON THE EXTINCTION CHARACTERISTICS OF METHANE VS. AIR COUNTERFLOW DIFFUSION FLAMES Michael A. Tanoff', Richard R. Dobbins, Mitchell D. Smooke Department of Mechanical Engineering, Yale University P.O. Boz 208284 New Haven, Connecticut, U.S.A. 06520-8284 Donald R. Burgess, Jr., Michael R. Zachariah, Wing Tsang Chemical Science and Technology Laboratory National Institute of Standanls and Technology Gaithersburg, Maryland, U.S.A. 20899-0001 Phillip R. Westmoreland Department of Chemical Engineering, University of Massachusetts Amherst, Massachusetts, U.S.A. 01009-9110 ABSTRACT Detailed numerical calculations are compared against available experiments and are used to inveg tigate the flame suppression and extinction properties of a variety of flourinated hydrocarbon candidates selected for halon 1301 and halon 1211 replacement. The air stream in a methane vs. air counterflow diffu- sion flame is doped with varying amountsof ChF,CH2F2, CHF3, CF4, CHFz-CFs and CHzF-CF3, as well as the diluents N2 and COz, and their effect on the strain rate required for flame extinction is monitored. The chemical model is based on a recently developed set of thermochemical and chemical kinetic data for the C1 and Cz fluorinated hydrocarbons. Numerical results are in very good agreement with available experimental data for CF4- and CHF3- suppresed methane vs. air counterflow diffusion flames. Both computations and experiments show similar linear decreases in required extinction strain rate with molar per cent agent added to the oxidizer stream, thereby yielding the same effectiveness for suppressing flames.
    [Show full text]
  • Burske Norbert W 195708 Phd
    "In presenting the dissertation as a partial fulfillment of the requirements for an advanced degree from the Georgia Institute of Technology, I agree that the Library of the Institution shall make it available for inspection and circulation in accordance with its regulations governing materials of this type. I agree that permission to copy from, or to publish from, this dissertation may be granted by the professor under whose direction it was written, or, in his absence, by the dean of the Graduate Division when such copying or publication is solely for scholarly purposes and does not involve potential financial gain. It is understood that any copying from, or publication of, this dissertation which involves potential financial gain will not be allowed without written permission. n It THE KINETICS OF THE BASE-CATALYZED DEUTERIUM EXCHANGE OF SOME HALOFORMS IN AQUEOUS SOLUTION A THESIS Presented to the Faculty of the Graduate Division Georgia Institute of Technology In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the School of Chemistry By Norbert William Burske June 1957 1< THE KINETICS OF THE BASE-CATALYZED DEUTERIUM EXCHANGE OF SOME HALOFORMS IN AQUEOUS SOLUTION Approved, J I ki Jack Hine I ,r Lod D. Frashier Erlft.Edg Grovenstein, Jr. Date Approved by Chairman, ii ACKNOWLEDGEMENT The author wishes to gratefully acknowledge his in- debtedness to Dr. J. Hine for invaluable guidance and without his aid this project would never have been completed. Also, the author is indebted to the Atomic Energy Commission and the Office of Ordnance Research, U. S. Army for sponsoring assistantships.
    [Show full text]