Chinese (Restaurant) Menu Translation Ting Liao 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

海鮮小炒 Vegetable on Rice L20 乾炒牛河 Fried Rice W/ Beef PT10 上海粗炒麵 六款 6 Items
現金九折 / 10% OFF WITH CASH 午市特價 $9.88 外賣餐單 自選和菜 LUNCH SPECIAL PARTY TRAY MENU TAKEOUT COMBO 供應時間:每日早上十一時至下午四時 跟明火例湯 兩款 2 Items ...........................................................$22.88 Available 11am - 4pm Daily 88 Daily Soup Included $39. 三款 3 Items ........................................................... $32.88 四款 4 items............................................................$42.88 百樂 PT1 揚州炒飯 PT9 乾燒伊麵 L1 梅菜扣肉飯 L19 上海粗 炒麵 Yeung Chow Fried Rice Braised E-Fu Noodle w/ 五款 5 Items ........................................................... $52.88 Braised Pork & Preserved Shanghai Noodle PT2 牛肉炒飯 Mushroom 海鮮小炒 Vegetable on Rice L20 乾炒牛河 Fried Rice w/ Beef PT10 上海粗炒麵 六款 6 Items ...........................................................$62.88 L2 涼瓜排骨飯 Rice Noodle w/ Beef & Soya Sauce PT3 雞粒炒飯 Shanghai Noodle Spare Ribs & Bitter Melon on Rice L21 菜遠牛河 Fried Rice w/ Chicken PT11 家鄉炒米 跟白飯例湯 L3 涼瓜牛肉飯 Rice Noodle w/ Beef & Soya Sauce PT4 蝦仁炒飯 Vermicelli Chinese Style Oriental Cuisine Beef & Bitter Melon on Rice L22 豉椒牛河 Fried Rice w/ Shrimp PT12 星洲炒米 Daily Soup & Steamed Rice Included Chef 88 L4 雲耳青瓜雞片飯 Rice Noodle w/ Beef & Black Bean PT5 雜菜炒飯 Singapore Vermicelli Fungus, Cucumber & Chicken on Sauce Fried Rice w/ Mixed PT13 乾炒牛河 T1 欖菜四季豆 T17 咕嚕雞球 Rice L23 芽菜仔炒麵 Vegetables Rice Noodle w/ Beef & Soya Stir Fried String Bean w/ Olive & Sweet & Sour Chicken L5 麻婆豆腐飯 Fried Noodle w/ Bean Sprouts PT6 海鮮炒飯 Sauce Minced Pork T18 藕片南乳腩肉 Ma Po Tofu w/ Minced Pork on L24 肉絲炒麵 Fried Rice w/ Seafood PT14 豉椒牛河 T2 咕嚕肉 Stir Fried Pork Belly w/ Lotus -

Price List – May 2020
Topmade Enterprises Ltd. Item Brand Description Pack Size Price Beef & Lamb 105700 Cargill Beef Shank Digital a appr. 21kg $17.50 kg 121010 Spr.Lamb Lamb Leg Bls NZ appr.11kg $18.85 kg Canned 370802 Mushroom Straw Whole Med 24/425g $45.00 cs 212007 Longevity Milk Sweet Condensed Milk 24/300ml $70.80 cs 212006 Carnation Milk Evaporated 48/354ml $84.96 cs Poultry 155013 TM Chic Leg/Thigh Meat Frz appr. 3/5kg $7.50 kg 150001 Fresh whole chic 1.6-1.8 (any brand) appr.25.5kg $7.20 kg 170104 Duck A 15-15.9kg CAN 6s 00015 appr.15.5kg $6.50 kg 150042 Chic Loong K.Fem.L 3-3.5lb 6s Frz 8.2-9.53kg $75.00 cs 156004 Chic breast boneless, skinless appr.3/5kg $10.95 kg 155002 Chic leg back attach app.20kg $3.99 kg Pork 130000 pork butt bnls fresh appr.24kg $6.50 kg 137000 Pork Belly Rind-On 2s Cov.19437 appr.12kg $13.50 kg 139403 Pork Side Rib 2.5cm(1") Trim D/Cut gwt 14.8kg $7.70 kg 139705 Pork Chop 1.3cm trim sharp bone c/c cut gwt appr.23.9kg $7.90 kg 139499 Pork Feet Front Split (4pc Cut) 13.60kg $7.60 kg 139807 Pork back bone appr.15kg $4.20 kg Tofu 402001 Tofu Bean Curd Fresh Med Firm 15/680g $27.00 cs 402004 Tofu Bean Curd Smooth Med Firm 2s 15/680g $27.00 cs Egg 160004 Eggs G.A Jumbo Brown 10dz(6/20s) $37.80 cs 160006 Eggs G.A X-Large White 15dz(6/30s) $51.50 cs Flour & Baking 240004 ELLISON Flour All Purpose BL 10kg 10kg $8.95 bg 245416 Hung Cheon Starch Wheat 50/454g $97.50 cs 245422 Erawan Flour Glutinous Rice 30/400g $41.07 cs 245425 Erawan Flour White Rice 30/400g $34.27 cs 245426 Cock Brand Starch Tapioca 60/400g $62.50 cs 245428 Erawan -

No. Stall Name Food Categories Address
No. Stall Name Food Categories Address Chi Le Ma 505 Beach Road #01-87, 1 吃了吗 Seafood Golden Mile Food Center 307 Changi Road, 2 Katong Laksa Laksa Singapore 419785 Duck / Goose (Stewed) Rice, Porridge & 168 Lor 1 Toa Payoh #01-1040, 3 Benson Salted Duck Rice Noodles Maxim Coffee Shop 4 Kampung Kia Blue Pea Nasi Lemak Nasi Lemak 10 Sengkang Square #01-26 5 Sin Huat Seafood Crab Bee Hoon 659 Lorong 35 Geylang 6 Hoy Yong Seafood Restaurant Cze Cha 352 Clementi Ave 2, #01-153 Haig Road Market and Food Centre, 13, #01-36 7 Chef Chik Cze Cha Haig Road 505 Beach Road #B1-30, 8 Charlie's Peranakan Food Eurasian / Peranakan / Nonya Golden Mile Food Centre Sean Kee Duck Rice or Duck / Goose (Stewed) Rice, Porridge & 9 Sia Kee Duck Rice Noodles 659-661Lor Lor 35 Geylang 665 Buffalo Rd #01-326, 10 545 Whampoa Prawn Noodles Prawn Mee / Noodle Tekka Mkt & Food Ctr 466 Crawford Lane #01-12, 11 Hill Street Tai Hwa Pork Noodle Bak Chor Mee Tai Hwa Eating House High Street Tai Wah Pork Noodle 531A Upper Cross St #02-16, Hong Lim Market & 12 大崋肉脞麵 Bak Chor Mee Food Centre 505 Beach Road #B1-49, 13 Kopi More Coffee Golden Mile Food Centre Hainan Fried Hokkien Prawn Mee 505 Beach Road #B1-34, 14 海南福建炒虾麵 Fried Hokkien Mee Golden Mile Food Centre 505 Beach Road #B1-21, 15 Longhouse Lim Kee Beef Noodles Beef Noodle Golden Mile Food Centre 505 Beach Road #01-73, 16 Yew Chuan Claypot Rice Claypot Rice Golden Mile Food Centre Da Po Curry Chicken Noodle 505 Beach Road #B1-53, 17 大坡咖喱鸡面 Curry Mee / Noodles Golden Mile Food Centre Heng Kee Curry Chicken Noodle 531A -
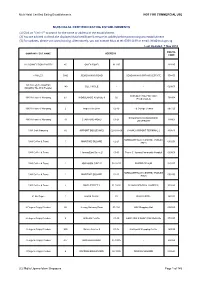
MUIS HALAL CERTIFIED EATING ESTABLISHMENTS (1) Click on "Ctrl + F" to Search for the Name Or Address of the Establishment
Muis Halal Certified Eating Establishments NOT FOR COMMERCIAL USE MUIS HALAL CERTIFIED EATING ESTABLISHMENTS (1) Click on "Ctrl + F" to search for the name or address of the establishment. (2) You are advised to check the displayed Halal certificate & ensure its validity before patronising any establishment. (3) For updates, please visit www.halal.sg. Alternatively, you can contact Muis at tel: 6359 1199 or email: [email protected] Last Updated: 7 Nov 2018 POSTAL COMPANY / EST. NAME ADDRESS CODE 126 CONNECTION BAKERY 45 OWEN ROAD 01-297 - 210045 13 MILES 596B SEMBAWANG ROAD - SEMBAWANG SPRINGS ESTATE 758455 149 Cafe @ TechnipFMC 149 GUL CIRCLE - - 629605 (Mngd By The Wok People) REPUBLIC POLYTECHNIC 1983 A Taste of Nanyang E1 WOODLANDS AVENUE 9 02 738964 (Food Court A) 1983 A Taste of Nanyang 2 Ang Mo Kio Drive 02-10 ITE College Central 567720 SINGAPORE MANAGEMENT 1983 A Taste of Nanyang 70 STAMFORD ROAD 01-21 178901 UNIVERSITY 1983 Cafe Nanyang 60 AIRPORT BOULEVARD 026-018-09 CHANGI AIRPORT TERMINAL 2 819643 HARBOURFRONT CENTRE, TRANSIT 1983 Coffee & Toast 1 MARITIME SQUARE 02-21 099253 AREA 1983 Coffee & Toast 1 Jurong East Street 21 01-01 Tower C, Jurong Community Hospital 609606 1983 Coffee & Toast 1 JOO KOON CIRCLE 02-32/33 FAIRPRICE HUB 629117 HARBOURFRONT CENTRE, TRANSIT 1983 Coffee & Toast 1 MARITIME SQUARE 02-21 099253 AREA 1983 Coffee & Toast 2 SIMEI STREET 3 01-09/10 CHANGI GENERAL HOSPITAL 529889 21 On Rajah 1 JALAN RAJAH 01 DAYS HOTEL 329133 4 Fingers Crispy Chicken 50 Jurong Gateway Road 01-15A JEM Shopping Mall 608549 4 Fingers -

Serving Certified Angus Steak
Appetizers & Soup Gado-Gado jicama, lettuce, fried prawn cake, tofu, peanut sauce $13.50 Satay Chicken $13.50, Beef or Combo Satay $14.95 chicken thigh or certified angus steak, cucumber, onion, peanut sauce Green Papaya & Mango Salad shrimps, roasted almond, kesom leaf $12.95 Fresh Hand Roll shrimps, bean sprouts, basil, peanut sauce $10.95 Sambal Anchovy onion, cucumber $8.50 Chicken Spring Roll deep fried, cabbage, basil, spicy sweet sauce $8.95 Roasted Shrimp Salad organic greens, fried thai basil, seasoned fruit, roasted almond, anaheim chili, himalayan salt $13.50 Grilled Pineapple Salad organic greens, fried thai basil, seasoned fruit, anaheim chili, roasted almond, himalayan salt $13.50 Roti Prata multi-layered home made Indian bread, curry sauce $4.25 **extra curry sauce: $3.50 Roti Telur multi-layered home made Indian bread with egg, curry sauce $7.95 Roti Murtabak multi-layered home made Indian bread with beef, egg, onion, curry sauce $14.50 Tofu Salad fried tofu triangles, jicama, cucumber, bean sprout, peanut sauce $13.50 Penang Poh Piah steamed spring rolls, jicama, dried shrimp, egg, lettuce, cucumber $8.95 Tom Yam Soup hot & sour, seafood or chicken, mushrooms, kaffer lime leaf, lemon grass $13.95 (small) $16.50 (large) Galangal & Kaffir Lime Soup seafood or chicken, coconut milk, mushroom, galangal $13.95 (small) $16.50 (large) Poultry Mango Chicken green & red pepper in mango shells $15.95 Sambal Malaysian Chicken belachan seasoning, curry leaf $15.95 Utama Basil Chicken snap peas, sweet onion, thai basil $15.50 Singaporean -

精彩萬千steamed 爽滑腸粉steamed Rice Noodle Roll
加 檯號 人數 ADD Table No. No. of Guests #_chef88elite 歡迎再度光臨!感謝您一直百樂軒 加 以來的支持並請保持安全 56 蒜蜜炸雞翼(六件) SP ADD 53 Crispy Chicken Wing w/ Honey Garlic (6 Pieces) 電話 Phone No. 22a 皇子菇豆苗腸 LWelcome back! Thank 57 椒鹽白飯魚 SP Snow Pea Leaf & King Mushroom Deep Fried Silver Fish w/ Spicy Salt 加 you for your continued ADD support and stay safe. Items 1-51a Are Available From 9am to 4pm 23 蜜汁叉燒腸 M 58 XO醬炒腸粉 SP BBQ Pork Pan Fried Rice Noodle Roll w/ XO Sauce 81 菜薳薑蔥撈生麵 $15.88 1-51a 項供應時間:上午九時至下午四時 Chef 88 Elite Egg Noodle w/ Ginger & Scallion 24 韭王豬潤腸粉 24 M 59 芽菜仔炒麵 SP 82 泰式茄瓜雞片河 $15.88 Pork Liver & Chive Fried Noodle w/ Bean Sprout 加 Thai Style Rice Noodle w/ Chicken ADD 精彩萬千 STEAMED 加 甜言蜜語 DESSERT ADD 60 沙薑鹽水雞腳 SP & Eggplant 煲煲暖意 RICE IN HOTPOT Chicken Feet w/ Ginger Powder Sauce 1 瑤柱海皇灌湯餃 XL 44 飄香榴槤酥 L 83 涼瓜爽肉炒麵 $15.88 Seafood Dumpling in Supreme Soup 25 香芋蒸排骨飯 XL Durian Puff 61 錦鹵炸雲吞 SP Crispy Chow Mein w/ Pork & Bitter Melon Pork Ribs & Taro Sweet & Sour Wonton 2 百樂水晶蝦餃皇 L 45a 香煎椰汁馬蹄糕 M 85 清湯牛腩河(例) $18.88 Crystal Shrimp Har Gow 26 臘味煲仔飯 XL Pan Fried Water Chestnut Cake 62 椒鹽雞軟骨 SP Rice Noodle w/ Beef Brisket 3 意大利瓜野菌餃 M Preserved Meat Deep Fried Chicken Knuckle in Soup (Regular) 26 46 酥皮蛋撻 L Mushroom & Zucchini Dumpling 27 北菇滑雞飯 XL Egg Tart 63 椒鹽豆腐角 SP 86 金沙涼瓜銀魚仔炒米粉 $16.88 Chicken & Mushroom Deep Fried Tofu w/ Spicy Salt Fried Vermicelli w/ Dried Fish, 4 皇子菇豆苗餃 M 47a 黑芝麻流沙煎堆 L Snow Pea Leaf & King Mushroom Dumpling 64 菠蘿咕嚕豬爽肉 SP Bitter Melon & Egg Yolk 生滾粥類 CONGEE Molten Black Sesame Ball 5 魚子醬燒賣 L Sweet & Sour Pork 87 梅菜扣肉炒飯 $16.88 49 香芒布甸 S Fried Rice -

Product List 4.22.14.Xlsx
! ! ! ! ! ! ! ! ! ! ! Produce & Groceries 52 15th Street ! Brooklyn ! NY ! 11215 ! 718-965-6500 www.seamarketny.com QUICK TIPS Do you need help locating a product? Hold the ‘Ctrl’ and ‘F’ buttons down, or the ‘Command’ and ‘F’ buttons if you are working off a Mac, to prompt the keyword search. If our product list contains the keyword, the keyword will be located and highlighted, to help navigate you through our inventory. Do you have questions, comments or concerns? Please contact us at [email protected] and our S.E.A. Market team will be more than happy to provide you with prices and product availability, even for items that you may not have been able to locate on our product list. We also have a team of food specialists that are available to provide recommendations on food handling, ingredient incorporation, and recipes upon request. What happens if an item is on back-order? Due to market fluctuations, product brand, packaging, and unit size are subject to change. In the off chance that an item is out of stock, we will try our best to locate and deliver a product of equal or better quality. If we cannot locate a product of equal or better quality, we will contact you as soon as possible. Upon delivery of the substitute item, we encourage you to inspect the order. If you are not happy with the quality of the substitute item, you are more than welcome to return the item to our S.E.A. Market driver. Category Item Code Description Brand U / M Unit Unit / CS Appetizers AP-526C Beef Satay A&A 100 CT CS AP-527C Chicken Satay A&A 100 CT CS -

The Rise of Disyllables in Old Chinese: the Role of Lianmian Words
City University of New York (CUNY) CUNY Academic Works All Dissertations, Theses, and Capstone Projects Dissertations, Theses, and Capstone Projects 2013 The Rise of Disyllables in Old Chinese: The Role of Lianmian Words Jian Li Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/3651 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] THE RISE OF DISYLLABLES IN OLD CHINESE: THE ROLE OF LIANMIAN WORDS by JIAN LI A dissertation submitted to the Graduate Faculty in Linguistics in partial fulfillment of the requirements for the degree of Doctor of Philosophy, The City University of New York 2013 © 2013 JIAN LI All Rights Reserved ii This manuscript has been read and accepted for the Graduate Faculty in Linguistics in satisfaction of the dissertation requirement for the degree of Doctor of Philosophy. Date Juliette Blevins, Ph.D. Chair of Examining Committee Date Gita Martohardjono, Ph.D. Executive Officer Supervisory Committee: Juliette Blevins, Ph. D Gita Martohardjono, Ph.D. William McClure, Ph.D. Outside Reader: Gopal Sukhu, Ph.D. THE CITY UNIVERSITY OF NEW YORK iii ABSTRACT THE RISE OF DISYLLABLES IN OLD CHINESE: THE ROLE OF LIANMIAN WORDS by JIAN LI ADVISER: PROFESSOR JULIETTE BLEVINS The history of Chinese language is characterized by a clear shift from monosyllabic to disyllabic words (Wang 1980). This dissertation aims to provide a new diachronic explanation for the rise of disyllables in the history of Chinese and to demonstrate its significance for Modern Chinese prosody and lexicalization. -

Sichuan Pork & Vegetable Dumplings 12 紅油炒手shanghai Pan Fried Minced Pork & Vegetable Buns 12 包豬肉生煎C
Spicy Singapore Pork & Shrimp Noodles 18 Chinese Sausage & Sun Dried Thai Iced Tea 7 Hot Chinese Tea 4 星洲米粉 Pork Belly with Cauliflower 28 泰式凍奶茶 中國熱茶 臘味炒臺山菜花 Hong Kong Style Beef Chow Fun 18 Iced Lemon Tea 5 Bubble Tea 8 香港牛肉炒河粉 Pork Cake With Salted Fish 26 冰紅茶 珍珠奶茶 咸魚肉餅 蒸或煎 Sichuan Pork & Vegetable Dumplings 12 Japanese Black Pepper Stir Fried Shrimp, 紅油炒手 Scallop & Squid Udon 18 Crispy Fried Rice 28 黑椒海鮮炒烏冬麫 14 Shanghai Pan Fried Minced Pork 脆米炒飯 Tiamo Rosé Buddha Beer 9 & Vegetable Buns 12 Yangzhou Shrimp & Pork Fried Rice 18 Seasoned Vegetables 玫瑰酒 開樂啤酒 包豬肉生煎 楊州炒飯 Any Style 24 清炒時蔬 Cantonese Crispy Shrimp Spring Roll 12 Cantonese Lo Mein 撈麵 18 Tiamo White Heineken 9 鮮蝦春卷 Choose One: Chicken, Beef, Pork, Shrimp or 白葡萄酒 喜力啤酒 Vegetable Chicken & Broccoli 18 鸡肉和西兰花 Shanghai Soup Dumplings 22 Combination (Any Two) Add 4 Tiamo Red Corona 9 雞肉,牛肉,豬肉,蝦,蔬菜 紅酒 科羅娜 上海小籠湯包 Beef & Broccoli 22 Korean Kim Chi Fried Rice 14 牛肉和西兰花 Tiamo Prosecco Bud Light 8 韓式泡菜炒飯 普羅塞科 百威淡啤 Shrimp & Broccoli 26 Three Cup Chicken 18 虾和西兰花 Taiwanese Beef Noodle Soup 18 Taiwanese Stir Fried Chicken with Basil & 台灣牛肉麪 Ginger 三柸雞 Cantonese Shrimp & Pork Wonton Noodle Pad Thai† 18 Soup 18 Wang Lo Kat 6 Choose One: Chicken, Beef, Pork, Shrimp 鮮蝦雲吞湯 (Any Two) Add 4 Chinese Cold Herbal Drink 王老吉 Contains Peanuts Malaysian Curry Beef Brisket Noodle Soup 18 泰式炒河粉 咖喱牛腩湯麵 Coconut Juice 7 椰清 Lobster Any Style 78 Cantonese Roasted Crispy Duck Lai Fun 波士頓龍蝦 Noodle Soup 22 Calpico 7 8 明爐吊燒鴨瀨粉 Japanese Yogurt Drink Whole Fish MP 優格氣水 Pistachio Or Vietnamese 清蒸海上鲜 Coffee Ice Cream, -

Rice & Rice Sticks, Noodles
RICE "J&P" HMONG LADY JASMINE RICE "J&P" 3 SISTER JASMINE RICE "BUFFALO" THAI JASMINE RICE RCHL50 RCTS RCBU (25#) (50#) (25#) (50#) (25#) (50#) "RABBIT" THAI JASMINE RICE "RABBIT" THAI SWEET RICE "BUFFALO" THAI SWEET RICE RCR RCRS RCBUS (5X10#) (25#) (50#) (25#) (50#) (25#) (50#) "RABBIT" BROKEN RICE "GOLDEN PHOENIX" JASMINE RICE "GOLDEN PHOENIX" BROKEN RICE RCRB RCGP RCGPB 25# (6 X 10#) (25#) (50#) (6 X 10#) (25#) (50#) 1 "KOKUHO" (YELLOW) "TSURU MAI" WHITE "T.ELEPHANTS"JASMINE "G.HARVEST"JASMINE RCK RCTM RCTEJ RCGH 100#, 50#, 20# 6X10# 50# 100# 25#, 50# 50# "MARUYU" RICE "TSURU MAI" BROWN "GOLDEN CRANE" "KODA" SWEET RICE RCM RCTMB RCGC RCKS 80#, 50# 50#, 20#, 6X5# 100#, 50#, 20#, 50#, 25#, 6X10#, 12X5# "APPLE" SWEET RICE "KOKUHO ROSE" (PINK) "BUFFALO"JASMINE RICE "BUFFALO"SWEET RICE RCAS RCKR RCBU4J RCBU4S 50#, 25#, 6X10#, 12X5# 50#, 20#, 4X10#, 8X5# 10 X 4# 10 X 4# DELTA RICE "L. ANGEL" JASMINE RICE "L. ANGEL" SWEET RICE CHINA BLACK JASMINE RCDT25 RCLAJ RCLAS RCCB 25# 10 X 4.4# 10 X 4.4# 1# 2# 4# 2 "APPLE" JASMINE RICE "BUDDHA" JASMINE RICE "PINK LOTUS" RICE RICELAND LONG GRAIN RCA1 RCBD50 RCPL50 RC50 50# 50# 50# 50# "DEER" JASMINE RICE "D.HORSES" JASMINE RICE "D.FLY" JASMINE RICE "3 LADIES" JASMINE RICE RCDJ RCDH RCDF RCTJ 25# 50# 25# 50# 25# 50# 25# 50# "RABBIT" "RABBIT" "3 SISTERS" "HMONG LADY" GUILIN VERMICELLI GUILIN FAMILY PACK INSTANT NOODLES INSTANT NOODLES RSRAG RSRAG2 RS3O RSHO 60 X 14oz 24 X 35.2oz 8 X 3.3# 8 X 3.3# "BUFFALO" "PARROT" LAI FUN CHIANG MAI VERMICELLI "RABBIT" VERMECELLI "HMONG LADY" VERM RSPL RSBUC RSRV RSHV 12 X 2# 12 X 2.2# (KP33) 15 X 28oz (#KB88) 15 X 28oz (#668) 3 ORIENTAL NOODLES (JUMBO PACK- GREEN) (FAMILY PACK-BLUE) "JP" LONG CHENG NOODLE 1MM. -

What Makes Ipoh Kueh Teow So Special by Chris Teh
FREE COPY JUNE 16 - 30, 2019 PP 14252/10/2012(031136) 30 SEN FOR DELIVERY TO YOUR DOORSTEP – ASK YOUR NEWSVENDOR ISSUE 306 100,000 print readers Bimonthly 1,685,645 online hits (May) – verifiable What makes Ipoh Kueh Teow so Special By Chris Teh Manual packing at Ipoh Kueh Teow and Noodles Sdn Bhd Kai Si Hor Fun poh has long been acknowledged to be the home of flat white noodles, more commonly known as hor fun in Cantonese or kway teow or spelt Ikueh teow in Hokkien. Flat rice noodles are also known as da fen in Sabah which means wide vermicelli. To dive deeper into how Ipoh kueh teow has garnered a reputation far and wide as being the best of its type of rice noodle, sought by foodies from all over Asia, Ipoh Echo went in search to uncover the source of its renown and why people flock to Ipoh to taste our inimitable “Kai Si Hor Fun” whether for breakfast, lunch, or dinner. FULL STORY ON PAGES 2 & 6 Varieties of coloured packaging for IKT products Ipoh Heritage Cycling Tour by Rosli Mansor Ahmad Razali by Rosli Mansor aking a ride through Ipoh, either by bicycle or trishaw, is an The second is by rickshaws and is dubbed the Rickshaw Ipoh experience in itself. Visitors get to feast their eyes on a myriad Heritage Tour. Duration is two hours too. It starts and ends at the Tof sights ranging from British colonial-era buildings to heri- same point. The machine can take two persons, one cycles the other tage sites steeped in history. -

UNESCO SITES in CHINA Your Guide to World Heritage Culture
Winter | 2018 UNESCO SITES IN CHINA Your Guide to World Heritage Culture Follow ISBN: 978-7-900747-945 Us on WeChat Now Advertising Hotline 400 820 8428 随刊付赠 城市家 出版发行:云南出版集团 云南科技出版责任有限公司 责任编辑:欧阳鹏 张磊 Urban Family Chief Editor Lena Gidwani 李娜 Copy Editor Matthew Bossons 马特 Production Supervisor Jack Lin 林川青 Designer Felix Chen 陈引全 Contributors: Students from various schools, Natalie Foxwell, Lauren Hogan, Kendra Perkins, Dr. Nate Balfanz, Alison Mary Cook, Leonard Stanley, Ellen Wang, Dr. Alfred Chambers, Celia Rayfiel, Mandy Tie, Sharon Raccah Perez, Sebastian Tosi Operations Shanghai (Head Office) 上海和舟广告有限公司 上海市蒙自路169号智造局2号楼305-306室 邮政编码:200023 Room 305-306, Building 2, No.169 Mengzi Lu, Shanghai 200023 电话:021-8023 2199 传真:021-8023 2190 Guangzhou 上海和舟广告有限公司广州分公司 广州市越秀区麓苑路42号大院2号610房 邮政编码:510095 Rm. 610, No.2 Building, Area 42, Lu Yuan Lu, Yuexiu District, Guangzhou 510095 电话:020-8358 6125, 传真:020-8357 3859-800 Beijing 北京业务联系 电话:010-8447 7002, 传真:010-8447 6455 Shenzhen 深圳业务联系 电话:0755-8623 3210, 传真:0755-8623 3219 CEO Leo Zhou 周立浩 National Digital Business Director Vickie Guo 郭韵 Digital Miller Yue 岳雷,Amanda Bao 包婷,Orange Wang 王爽,Yu Sun 孙宇,Elsa Yang 杨融,Kane Zhu 朱晓俊 General Manager Henry Zeng 曾庆庆 Operations Manager Rachel Tong 童日红 Finance Assistant Sunnie Lv 吕敏瑜 Sales Managers Celia Yu 余家欣, Justin Lu 卢建伟 Account Manager Wesley Zhang 张炜 Senior BD Executive Nicole Tang 汤舜妤 Account Executives Annie Li 李泳仪, Tia Weng 翁晓婷 Marketing Supervisor Fish Lin 林洁瑜 Senior Marketing Executive Shumin Li 黎淑敏 Marketing Executives Peggy Ni 倪佩琪, Kathy Chen 陈燕筠 Sales