DOCSLIB.ORG

KO-DISSERTATION-2020.Pdf (3.093Mb)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
KO-DISSERTATION-2020.Pdf (3.093Mb) ABSTRACT Multi-pulse Nonlinear Optical Spectroscopy and Light-matter Interactions in Layered Materials Brian Alexander Ko, Ph.D. Mentor: Marlan O. Scully, Ph.D. The interaction between light and matter is one that underscores many applications from solar energy conversion to optical sensing of biological materials. The use of multiple pulses to study these interactions are especially useful in understanding the nonlinear optical properties of materials. Transition metal dichalcogenides such as molybdenum disulfide (MoS2) are attractive materials due to the existence of a direct excitonic resonance that can be used to enhance nonlinear optical phenomena, such as Raman spectroscopy. Here, we have investigated four-wave mixing (FWM) processes in bulk MoS2 using a multiplex coherent anti-Stokes Raman spectroscopy setup. The observed FWM signal has a resonance at approximately 680 nm, corresponding to the energy of the A excitonic transition of MoS2. This resonance can be attributed to the increased third-order nonlinear susceptibility near the excitonic transition. This phenomenon shows the potential of MoS2 as a substrate for enhancing FWM processes. Understanding how particles and light interact in a liquid environment is vital for optical and biological applications. The interaction between two femtosecond pulses and MoS2 nanoparticles suspended in liquid is studied. The laser pulses induce bubble formation on the surface of a nanoparticle and a nanoparticle aggregate then forms on the surface of the trapped bubble. Two-dimensional organometallic lead halide perovskites are generating great interest due to their optoelectronic characteristics, such as a direct band gap in the visible regime. However, the presence of defect states within the crystal structure can affect these properties, resulting in changes to their emission and the emergence of nonlinear optical phenomena. Here, we have investigated the effects of the presence of defect states on the nonlinear optical phenomena of the hybrid perovskite (BA)2(MA)2Pb3Br10. When two pulses are incident on a perovskite flake, FWM occurs, with peaks corresponding to the defect energy levels present within the crystal. The longer lifetime of the defect state, in comparison to that of virtual transitions, allows for a larger population of electrons to be excited by the second pump photon, resulting in increased FWM signal at the defect energies. This technique has the potential to detect defect energy levels in bulk crystals using FWM. Multi-pulse Nonlinear Optical Spectroscopy and Light-matter Interactions in Layered Materials by Brian Alexander Ko, B.S. A Dissertation Approved by the Department of Physics Dwight P. Russell, Ph.D., Interim Chairperson Submitted to the Graduate Faculty of Baylor University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Approved by the Dissertation Committee Marlan Scully, Ph.D., Chairperson Ho Wai Howard Lee, Ph.D. Zhenrong Zhang, Ph.D. Truell Hyde, Ph.D. Jonathan Hu, Ph.D. Accepted by the Graduate School December 2020 J. Larry Lyon, Ph.D., Dean Page bearing signatures is kept on file in the Graduate School. Copyright © 2020 by Brian Alexander Ko All rights reserved TABLE OF CONTENTS LIST OF FIGURES ......................................................................................................... vii LIST OF TABLES ............................................................................................................ ix ACKNOWLEDGMENTS .................................................................................................. x ATTRIBUTIONS ............................................................................................................ xii CHAPTER ONE ................................................................................................................. 1 Introduction ............................................................................................................. 1 Enhanced Four-wave Mixing Process Near the Excitonic Resonances of Bulk MoS2 ........................................................................................................... 2 Multi-pulse Laser-Induced Bubble Formation and Nanoparticle Aggregation Using MoS2 Nanoparticles .......................................................................... 4 Resonant Degenerate Four-wave Mixing at the Defect Energy Levels of 2D Organic-inorganic Hybrid Perovskite Crystals ................................. 9 CHAPTER TWO .............................................................................................................. 13 Degenerate Multiplex Coherent anti-Stokes Raman Spectroscopy Setup .............13 Derivation of Spontaneous Raman Cross-Section .....................................13 Selection Rules for Raman Transitions ......................................................15 Degenerate Multiplex Coherent Anti-Stokes Raman Spectroscopy Setup ........................................................................17 CHAPTER THREE .......................................................................................................... 21 Enhanced Four-wave Mixing Process Near the Excitonic Resonances of Bulk MoS2 ................................................................................................. 21 Abstract ................................................................................................................. 21 Introduction ........................................................................................................... 21 Methods................................................................................................................. 23 Results ................................................................................................................... 25 Degenerate Four-wave Mixing on Bulk MoS2 ......................................... 25 Discussion ............................................................................................................. 31 Degenerate Four-wave Mixing at the Excitonic Resonance ......................31 Thickness Dependence of Four-wave Mixing .......................................... 32 Calculation of the Third-order Nonlinear Susceptibility ...........................33 Acknowledgments................................................................................................. 35 CHAPTER FOUR ............................................................................................................. 36 Multi-pulse Laser-Induced Bubble Formation and Nanoparticle Aggregation Using MoS2 Nanoparticles ........................................................................ 36 Abstract ..................................................................................................... 36 v Introduction ............................................................................................... 36 Results ....................................................................................................... 39 Laser-Induced Cavitation and Nanoparticle Aggregation ............ 39 Laser-Induced Bubble Rotation and Convection ...........................42 Nanoparticle Aggregation ..............................................................44 Pulse Dependence .....................................................................................45 Discussion ..................................................................................................49 Pulse Dependence of Bubble Formation....................................... 49 Bubble Heating ............................................................................. 50 Comparison with Other Nanoparticles .......................................... 52 Methods..................................................................................................... 55 Acknowledgments..................................................................................... 57 CHAPTER FIVE .............................................................................................................. 58 Resonant Degenerate Four-wave Mixing at the Defect Energy Levels of 2D Organic-inorganic Hybrid Perovskite Crystals ............................... 58 Abstract ..................................................................................................... 58 Introduction ............................................................................................... 59 Methods..................................................................................................... 62 Results ....................................................................................................... 65 Discussion ................................................................................................. 70 Acknowledgments..................................................................................... 73 CHAPTER SIX ................................................................................................................ 74 Conclusion ........................................................................................................... 74 Enhanced Four-wave Mixing Process Near the Excitonic Resonances of Bulk MoS2 ........................................................... 74 Multi-pulse Laser-Induced Bubble Formation and Nanoparticle Aggregation Using MoS2 Nanoparticles ...................................... 74 Resonant Degenerate Four-wave Mixing at the Defect Energy Levels of 2D Organic-inorganic Hybrid Perovskite Crystals ...... 75 APPENDIX
Load more

Recommended publications
  • Frontiers of Quantum and Mesoscopic Thermodynamics 29 July - 3 August 2013, Prague, Czech Republic
    Frontiers of Quantum and Mesoscopic Thermodynamics 29 July - 3 August 2013, Prague, Czech Republic Under the auspicies of Ing. Milosˇ Zeman President of the Czech Republic Milan Stˇ echˇ President of the Senate of the Parliament of the Czech Republic Prof. Ing. Jirˇ´ı Drahos,ˇ DrSc., dr. h. c. President of the Academy of Sciences of the Czech Republic Dominik Cardinal Duka OP Archbishop of Prague Supported by • Committee on Education, Science, Culture, Human Rights and Petitions of the Senate of the Parliament of the Czech Republic • Institute of Physics, the Academy of Sciences of the Czech Republic • Institute for Theoretical Physics, University of Amsterdam, The Netherlands • Department of Physics, Texas A&M University, USA • Institut de Physique Theorique,´ CEA/CNRS Saclay, France Topics • Foundations of quantum physics • Non-equilibrium statistical physics • Quantum thermodynamics • Quantum measurement, entanglement and coherence • Dissipation, dephasing, noise and decoherence • Quantum optics • Macroscopic quantum behavior, e.g., cold atoms, Bose-Einstein condensates • Physics of quantum computing and quantum information • Mesoscopic, nano-electromechanical and nano-optical systems • Biological systems, molecular motors • Cosmology, gravitation and astrophysics Scientific Committee Chair: Theo M. Nieuwenhuizen (University of Amsterdam) Co-Chair: Vaclav´ Spiˇ ckaˇ (Institute of Physics, Acad. Sci. CR, Prague) Raymond Dean Astumian (University of Maine, Orono) Roger Balian (IPhT, Saclay) Gordon Baym (University of Illinois at Urbana
    [Show full text]
  • Delayed-Choice Gedanken Experiments and Their Realizations
    REVIEWS OF MODERN PHYSICS, VOLUME 88, JANUARY–MARCH 2016 Delayed-choice gedanken experiments and their realizations Xiao-song Ma* Institute for Quantum Optics and Quantum Information (IQOQI), Austrian Academy of Sciences, Boltzmanngasse 3, 1090 Vienna, Austria, Department of Electrical Engineering, Yale University, 15 Prospect Street, New Haven, Connecticut 06520, USA, and National Laboratory of Solid State Microstructures, School of Physics, Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China † Johannes Kofler Max Planck Institute of Quantum Optics (MPQ), Hans-Kopfermann-Straße 1, 85748 Garching, Germany ‡ Anton Zeilinger Vienna Center of Quantum Science and Technology (VCQ), University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria and Institute for Quantum Optics and Quantum Information (IQOQI), Austrian Academy of Sciences, Boltzmanngasse 3, 1090 Vienna, Austria (published 3 March 2016) The wave-particle duality dates back to Einstein’s explanation of the photoelectric effect through quanta of light and de Broglie’s hypothesis of matter waves. Quantum mechanics uses an abstract description for the behavior of physical systems such as photons, electrons, or atoms. Whether quantum predictions for single systems in an interferometric experiment allow an intuitive under- standing in terms of the particle or wave picture depends on the specific configuration which is being used. In principle, this leaves open the possibility that quantum systems always behave either definitely as a particle or definitely as a wave in every experimental run by a priori adapting to the specific experimental situation. This is precisely what is tried to be excluded by delayed-choice experiments, in which the observer chooses to reveal the particle or wave character of a quantum system—or even a continuous transformation between the two—at a late stage of the experiment.
    [Show full text]
  • Works of Love
    reader.ad section 9/21/05 12:38 PM Page 2 AMAZING LIGHT: Visions for Discovery AN INTERNATIONAL SYMPOSIUM IN HONOR OF THE 90TH BIRTHDAY YEAR OF CHARLES TOWNES October 6-8, 2005 — University of California, Berkeley Amazing Light Symposium and Gala Celebration c/o Metanexus Institute 3624 Market Street, Suite 301, Philadelphia, PA 19104 215.789.2200, [email protected] www.foundationalquestions.net/townes Saturday, October 8, 2005 We explore. What path to explore is important, as well as what we notice along the path. And there are always unturned stones along even well-trod paths. Discovery awaits those who spot and take the trouble to turn the stones. -- Charles H. Townes Table of Contents Table of Contents.............................................................................................................. 3 Welcome Letter................................................................................................................. 5 Conference Supporters and Organizers ............................................................................ 7 Sponsors.......................................................................................................................... 13 Program Agenda ............................................................................................................. 29 Amazing Light Young Scholars Competition................................................................. 37 Amazing Light Laser Challenge Website Competition.................................................. 41 Foundational
    [Show full text]
  • Frontiers of Quantum and Mesoscopic Thermodynamics 14 - 20 July 2019, Prague, Czech Republic
    Frontiers of Quantum and Mesoscopic Thermodynamics 14 - 20 July 2019, Prague, Czech Republic Under the auspicies of Ing. Miloš Zeman President of the Czech Republic Jaroslav Kubera President of the Senate of the Parliament of the Czech Republic Milan Štˇech Vice-President of the Senate of the Parliament of the Czech Republic Prof. RNDr. Eva Zažímalová, CSc. President of the Czech Academy of Sciences Dominik Cardinal Duka OP Archbishop of Prague Supported by • Committee on Education, Science, Culture, Human Rights and Petitions of the Senate of the Parliament of the Czech Republic • Institute of Physics, the Czech Academy of Sciences • Department of Physics, Texas A&M University, USA • Institute for Theoretical Physics, University of Amsterdam, The Netherlands • College of Engineering and Science, University of Detroit Mercy, USA • Quantum Optics Lab at the BRIC, Baylor University, USA • Institut de Physique Théorique, CEA/CNRS Saclay, France Topics • Non-equilibrium quantum phenomena • Foundations of quantum physics • Quantum measurement, entanglement and coherence • Dissipation, dephasing, noise and decoherence • Many body physics, quantum field theory • Quantum statistical physics and thermodynamics • Quantum optics • Quantum simulations • Physics of quantum information and computing • Topological states of quantum matter, quantum phase transitions • Macroscopic quantum behavior • Cold atoms and molecules, Bose-Einstein condensates • Mesoscopic, nano-electromechanical and nano-optical systems • Biological systems, molecular motors and
    [Show full text]
  • A Fiber Optic Fluorometric Sensor for the Detection of Polymerase Chain Reaction (PCR)–Amplified DNA [26]
    Nanophotonics 2021; 10(1): 235–246 Research article Navid Rajil, Alexei Sokolov, Zhenhuan Yi, Garry Adams, Girish Agarwal, Vsevolod Belousov, Robert Brick, Kimberly Chapin, Jeffrey Cirillo, Volker Deckert, Sahar Delfan, Shahriar Esmaeili, Alma Fernández-González, Edward Fry, Zehua Han, Philip Hemmer, George Kattawar, Moochan Kim, Ming-Che Lee, Chao-Yang Lu, Jon Mogford, Benjamin Neuman, Jian-Wei Pan, Tao Peng, Vincent Poor, Steven Scully, Yanhua Shih, Szymon Suckewer, Anatoly Svidzinsky, Aart Verhoef, Dawei Wang, Kai Wang, Lan Yang, Aleksei Zheltikov, Shiyao Zhu, Suhail Zubairy and Marlan Scully* A fiber optic–nanophotonic approach to the detection of antibodies and viral particles of COVID-19 https://doi.org/10.1515/nanoph-2020-0357 to detect anthrax in real-time. A variation on the laser Received July 1, 2020; accepted August 31, 2020; published online spectroscopic techniques we developed for the rapid detec- September 29, 2020 tion of anthrax can be applied to detect the Severe Acute Respiratory Syndrome-Corona Virus-2 (SARS-CoV-2 virus). In Abstract: Dr. Deborah Birx, the White House Coronavirus addition to detecting a single virus, this technique allows us Task Force coordinator, told NBC News on “Meet the Press” to read its surface protein structure. In particular, we have that “[T]he U.S. needs a ‘breakthrough’ in coronavirus testing been conducting research based on a variety of quantum to help screen Americans and get a more accurate picture of optical approaches aimed at improving our ability to detect the virus’ spread.” We have been involved with biopathogen Corona Virus Disease-2019 (COVID-19) viral infection. detection since the 2001 anthrax attacks and were the first Neurotechnologies of the Federal Medical Biological Agency, Moscow The list of coauthors represents only a fraction of the team working on 117997, Russia the real-time detection of pathogens from anthrax to SARS-CoV-2.
    [Show full text]
  • Julio Gea-Banaclochea 'Department of Physics, University of Arkansas, Fayett,Eville, Arkansas, 72701, USA
    Geometric phase gate with a quantized driving field Shabnam Siddiquia arid Julio Gea-Banaclochea 'Department of Physics, University of Arkansas, Fayett,eville, Arkansas, 72701, USA ABSTRACT We have studied the performance of a geometric phase gate with a quantized driving field numerically, and developed an analytical approximation that yields some preliminary insight on the way the nl~hltbecomes entangled with the driving field. Keywords: Quantum computation, adiabatic quantum gates, geometric quantum gates 1. INTRODUCTION It was first suggested by Zanardi and ~asetti,'that the Berry phase (non-abelian holon~m~)~-~might in principle provide a novel way for implementing universal quantum computation. They showed that by encoding quantum information in one of the eigenspaces of a degenerate Harniltonian H one can in principle achieve the full quantum computational power by using holonomies only. It was then thought that since Berry's phase is a purely geometrical effect, it is resilient to certain errors and may provide a possibility for performing intrinsically fault-tolerant quantum gate operations. In a paper by Ekert et.al,5 a detailed theory behind the implementation of geometric computation was developed and an implementation of a conditional phase gate in NMR was shown by Jones et.al.6 This attracted the attention of the research community and various studies were performed to study the rob~stness~-'~of geometric gates and the implementation of these gates in other systenls such as ion-trap, solid state and Josephson qubits.lO-l4 In this paper we study an adiabatic geometric phase gate when the control system is treated as a two mode quantized coherent field.
    [Show full text]
  • Remote Detection Via Quantum Coherence Professor Marlan O
    Paint Branch Distinguished Lecture in Applied Physics The Paint Branch Distinguished Lecture in Applied Physics was established and endowed by a generous gift to IREAP in 2014 with the intention to bring luminaries in the field of Applied Physics to speak to our community. We hope that this lecture will bring together students, faculty, and community members to celebrate research that dissolves the boundaries of classic disciplines. This is the inaugural Lecture. Remote Detection via Quantum Coherence Professor Marlan O. Scully Baylor, Princeton, and Texas A&M Universities Monday, October 19, 2015 4 p.m., Room 1101 Biosciences Research Building Abstract: There is nothing so practical as a good theory. As a case in point, the compelling need for standoff detection of hazardous gases and vapor indicators of explosives has motivated the development of remotely pumped schemes that produce radiation in the backward direction [1,2]. Moving from conceptualization to theoretical analysis and experimental verification, we demonstrate that high gain can be achieved in air. Backward air lasing provides possibilities for remote detection [3], as will be discussed. Bio: Marlan Scully (Baylor, Princeton, and Texas A&M) has worked on a variety of problems in laser physics and quantum optics, including: the first quantum theory of the laser with Lamb, the laser phase transition analogy and its applications to the Bose condensate, experimental demonstrations of lasing without inversion, and ultraslow light in hot gases via quantum coherence. His introduction of entanglement interferometry to quantum optics has shed light on the foundations of quantum mechanics, e.g., the quantum eraser. Recently he and his colleagues have applied quantum coherence to remote sensing of anthrax and probing through turbid mediums, such as skin and plant tissue.
    [Show full text]
  • Výroční Zpráva FZU Za Rok 2019
    Výroční zpráva o činnosti a hospodaření za rok 2019 FZÚ AV ČR, V. V. I. VÝROČNÍ ZPRÁVA 2019 vodní slovo k výroční zprávě je velmi specifický slohový útvar. Mělo by jít Úo ohlédnutí za minulým rokem, ovšem vzniká typicky až jako jedna z posledních součástí výroční zprávy v květnu roku aktuálního. Ředitel – pisatel je tak vystaven velkému pokušení zohlednit důležité události, které se udály v posledních měsících. Toto pokušení je obzvláště silné v letošním roce, kdy nedávné události v rámci koronavirové krize a nouzového stavu v České republice byly opravdu mimořádné a historicky jedinečné, ale omezím se nyní na konstatování, že Fyzikálnímu ústavu AV ČR (FZU) se v této zkoušce podařilo obstát mimořádně dobře – zejména díky vynikajícímu nasazení všech zaměstnanců v mnoha různých rolích. Rok 2019 byl pro rozvoj FZU rokem jistě příznivým. Všechny relevantní statistické ukazatele rostly: Počet zaměstnanců se zvýšil z 1334 na konci roku 2018 na 1357 na konci roku 2019. Jde o růst jen o 1,7 %, což je ale v souladu s tím, že obě velká laserová centra ELI Beamlines a HiLASE již jsou plně personálně obsazena a ani v jiných vědeckých sekcích nebyl v loňském roce zahájen žádný projekt spojený se zásadnějším přijímáním nových lidí. Provozní rozpočet FZU – plánovaný – stoupl z 1,7 miliardy Kč v roce 2018 na 1,9 miliardy Kč v roce 2019. To svědčí o tom, že FZU se zatím daří nalézat financování pro rostoucí počet zaměstnanců i finanční prostředky pro to, aby tito zaměstnanci mohli provádět špičkový výzkum. Tato aritmetika je trochu komplikovaná ze dvou důvodů – účetně se do provozního rozpočtu promítají i odpisy dlouhodobého majetku, takže reálnější hodnotu skutečně provozního rozpočtu bychom dostali, kdybychom odečetli kolem 400 miliónů Kč v obou letech.
    [Show full text]
  • What If the Earth Stopped Spinning? 3 Maser to Predict Milky Way's Fate 8
    What if the Earth stopped spinning? 3 Maser to predict Milky Way's fate 8 Will we ever glimpse the universe's first stars? 10 When is a group of stars not a galaxy? 12 Telltale chemistry could betray ET 14 Online games reveal players' personalities – to who? 16 Compact 'eyeball' camera stretches to zoom 18 PirateBox lets you share files with anyone close by 20 Spinning seeds inspire single-bladed helicopters 21 VW's diesel hybrid: most efficient car on the planet? 23 Parallel parking is better for pedestrians' health 25 Soft-centred fossils reveal dinosaurs' true colours 27 How the seahorse gained its shapely body 31 Mad cow disease is almost extinct globally 32 Transsexual differences caught on brain scan 35 Kids with low self-control are less successful adults 37 Royal rumpus over King Tutankhamun's ancestry 38 Stretchy DNA shows off its elastic qualities 40 Remember the lessons of past clinical trials abuses 42 Quantum reality: The many meanings of life 44 Ancient puzzle gets new lease of 'geomagical' life 49 Deep meaning in Ramanujan's 'simple' pattern 52 Cancer Drug Aids Regeneration of Spinal Cord After Injuries 54 Dinosaurs Survived Mass Extinction by 700,000 Years, Fossil Find Suggests 56 A Mix of Tiny Gold and Viral Particles, and the DNA Ties That Bind Them 58 How Bacteria Keep Ahead of Vaccines and Antibiotics 60 Warming North Atlantic Water Tied to Heating Arctic 63 Brain 'GPS' Illuminated in Migratory Monarch Butterflies 66 Mass Extinction Linked to Ancient Climate Change, New Details Reveal 68 Modern Humans Reached Arabia
    [Show full text]
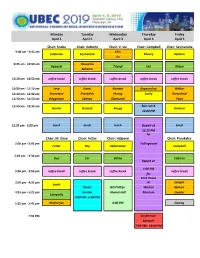
  • UBEC 2019 Abstract Book (PDF)
    Monday Tuesday Wednesday Thursday Friday April 1 April 2 April 3 April 4 April 5 Chair: Snoke Chair: Ketterle Chair: V. Liu Chair: Campbell Chair: Szymanska 9:00 am ‐ 9:45 am Shin Svistunov Szymanska Khoury Ketterle Jin 9:45 am ‐ 10:30 am Pieczarka Halperin Trivedi Hui Kirton Ballarini 10:30 am ‐ 10:50 am coffee break coffee break coffee break coffee break coffee break 10:50 am ‐ 11:10 am Levy Kanai Rontani Boyanovksy Walker 11:10 am ‐ 11:30 am Kuznetsov Proukakis Huang Scully Kurtscheid 11:30 am ‐ 11:50 am Briggeman Salman Giamarchi Yoon 11:50 am ‐ 12:35 am Box Lunch Demler Groszek Ruegg Siemens 12:00 PM 12:35 pm ‐ 2:00 pm lunch lunch lunch Depart at lunch 12:15 PM for Chair: M. Chan Chair: Fetter Chair: Halperin Chair: Proukakis 2:00 pm ‐ 2:45 pm Fallingwater Fetter Rey Abbamonte Campbell 2:45 pm ‐ 3:30 pm Guo Lin Bailey Cabrera Depart at 1:00 PM 3:30 pm ‐ 3:50 pm coffee break coffee break coffee break coffee break for Frick House 3:50 pm ‐ 4:35 pm or Langen Smith Poster Bill Phillips Warhol Akimov 4:35 pm ‐ 5:25 pm Session Alumni Hall Museum Quader Lebreuilly 4:00 PM ‐ 6:00 PM 5:25 pm ‐ 5:45 pm Mukherjee 4:00 PM Closing 7:30 PM Conference Banquet 7:30 PM ‐ 10:00 PM ~ ~VJ 1 \ \ ~\ ~ D ~ .,, \ VJ SlhAvenue I j .,, J '' m ifJ jOOCa<e St 0, 4 .. 'VJ~\ Pittsburgh Oakland II Buy 1. Caliban Book Shop • See and Do 2.
    [Show full text]
  • Light, the Universe and Everything – 12 Herculean Tasks for Quantum Cowboys and Black Diamond Skiers
    Journal of Modern Optics ISSN: 0950-0340 (Print) 1362-3044 (Online) Journal homepage: http://www.tandfonline.com/loi/tmop20 Light, the universe and everything – 12 Herculean tasks for quantum cowboys and black diamond skiers Girish Agarwal, Roland E. Allen, Iva Bezděková, Robert W. Boyd, Goong Chen, Ronald Hanson, Dean L. Hawthorne, Philip Hemmer, Moochan B. Kim, Olga Kocharovskaya, David M. Lee, Sebastian K. Lidström, Suzy Lidström, Harald Losert, Helmut Maier, John W. Neuberger, Miles J. Padgett, Mark Raizen, Surjeet Rajendran, Ernst Rasel, Wolfgang P. Schleich, Marlan O. Scully, Gavriil Shchedrin, Gennady Shvets, Alexei V. Sokolov, Anatoly Svidzinsky, Ronald L. Walsworth, Rainer Weiss, Frank Wilczek, Alan E. Willner, Eli Yablonovitch & Nikolay Zheludev To cite this article: Girish Agarwal, Roland E. Allen, Iva Bezděková, Robert W. Boyd, Goong Chen, Ronald Hanson, Dean L. Hawthorne, Philip Hemmer, Moochan B. Kim, Olga Kocharovskaya, David M. Lee, Sebastian K. Lidström, Suzy Lidström, Harald Losert, Helmut Maier, John W. Neuberger, Miles J. Padgett, Mark Raizen, Surjeet Rajendran, Ernst Rasel, Wolfgang P. Schleich, Marlan O. Scully, Gavriil Shchedrin, Gennady Shvets, Alexei V. Sokolov, Anatoly Svidzinsky, Ronald L. Walsworth, Rainer Weiss, Frank Wilczek, Alan E. Willner, Eli Yablonovitch & Nikolay Zheludev (2018) Light, the universe and everything – 12 Herculean tasks for quantum cowboys and black diamond skiers, Journal of Modern Optics, 65:11, 1261-1308, DOI: 10.1080/09500340.2018.1454525 To link to this article: https://doi.org/10.1080/09500340.2018.1454525 Published online: 24 Apr 2018. Submit your article to this journal Article views: 4956 View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=tmop20 JOURNAL OF MODERN OPTICS, 2018 VOL.
    [Show full text]
  • Symposium on Recollision Physics 2018 Chateau Montebello, Quebec
    6\PSRVLXPRQ5HFROOLVLRQ3K\VLFV &KDWHDX0RQWHEHOOR4XHEHF&DQDGD 0D\±0D\ Chairs Francois Légaré Sylvain Charbonneau Institut national de la recherche scientifique University of Ottawa [email protected] [email protected] André Staudte David M. Villeneuve National Research Council of Canada National Research Council of Canada [email protected] [email protected] Indispensable help is gratefully acknowledged: Jennifer Vuong, Stephen Lee, Philippe-Thierry Douamba, Zack Dube 1 Internet Access INTERNET PASSCODE 3STEPS CONNECTION INSTRUCTIONS 1. For Wired Service: Connect the network cable to your device. For Wireless Service: Turn on the wireless service on your device, and if prompted, connect to the wireless network. 2. Open your web browser. This should automatically bring up the login page. if not please, type login.globalsuite.net into the web browser address bar and press Enter. You should now see the login page. if you still don't see the login page, please ensure you are connected to the correct wireless network (See step 1). 3. Follow the on-screen instructions, and accept the terms of service. To access service options after loggin in, type services.globalsuite.net into the web browser ad- dress bar and press Enter. iPod, iPhone and iPad 1. Tap on Settings 2. Select Wi-Fi 3. Confirm that the Wi-Fi slider is ON 4. Select the network 5. Continue with the login process from Step 2 in the previous section Should you require any assistance, please call our Fairmont Internet “HelpDesk” by dialing 1-888-240-3736. You may also dial “0” and ask the telephone operator to connect you with the “HelpDesk”.
    [Show full text]