DOCSLIB.ORG

Copyright and Use of This Thesis This Thesis Must Be Used in Accordance with the Provisions of the Copyright Act 1968

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Copyright and Use of This Thesis This Thesis Must Be Used in Accordance with the Provisions of the Copyright Act 1968 COPYRIGHT AND USE OF THIS THESIS This thesis must be used in accordance with the provisions of the Copyright Act 1968. Reproduction of material protected by copyright may be an infringement of copyright and copyright owners may be entitled to take legal action against persons who infringe their copyright. Section 51 (2) of the Copyright Act permits an authorized officer of a university library or archives to provide a copy (by communication or otherwise) of an unpublished thesis kept in the library or archives, to a person who satisfies the authorized officer that he or she requires the reproduction for the purposes of research or study. The Copyright Act grants the creator of a work a number of moral rights, specifically the right of attribution, the right against false attribution and the right of integrity. You may infringe the author’s moral rights if you: - fail to acknowledge the author of this thesis if you quote sections from the work - attribute this thesis to another author - subject this thesis to derogatory treatment which may prejudice the author’s reputation For further information contact the University’s Director of Copyright Services sydney.edu.au/copyright Advanced NMR Spectral Characteristics Used in Biochemical Studies of Anisotropic Media and Cells New Ways of Analysing Quadrupolar-Split Resonances, Dynamically Hyperpolarised Spectra, and Those Obtained With Shift Reagents Max Puckeridge, BSc(Hons) A thesis submitted for the degree of Doctor of Philosophy January 2014 School of Molecular Bioscience University of Sydney NSW 2006 Australia i Acknowledgements I wish to thank my supervisor, Professor Philip Kuchel, for the large role he played in my development as a scientist and a person. He showed an incredible commitment to me despite travelling to Singapore and becoming the head of a research institute. I am very grateful for the skills, and attention to detail, that I developed while working with him. I would like to thank Professor Arthur Conigrave, my associate supervisor, for his guidance and allowing me to participate in his group meetings while Philip was overseas. Also, I would thank Bob Chapman who was always reliable for advice and help on the NMR spectrometer. I am thankful to the other Kuchel students for mentoring me during my first year, particularly Tsz Wai Yau, who trained me in DIC microscopy and RBC preparation. I would also thank Guilhem Pag`esfor running the DNP NMR experiments in Paper II, and the many technicians in the Biochemistry building who ran glucose assays for Paper V. Last I would thank all my family. I am grateful to my sister Carla, for her support, and my parents, who allowed me to do my best and get a good education. And of course, my soul mate and partner Jana, who always keenly discussed my work and even listened to my constant ‘math talk’. ii Abstract The theme of this thesis was to quantify possible sources of adenosine triphosphate (ATP) hydrolysis in the human red blood cell (RBC). Understanding the consumption of ATP in RBCs provides insight into its energy demands, and those of other cell types and the body as a whole. The main sources of ATP hydrolysis investigated included: (i) the Na+,K+-ATPase (NKA); and (ii) cell membrane flickering (CMF) of RBCs. In addition to these studies, we developed mathematical models of RBC systems and the experimental techniques used. Many of these models described spectral characteristics of NMR spectra, including: (i) chemical shift differences induced by shift reagents (SRs); (ii) dynamic nuclear polarisation (DNP) NMR; and (iii) z-spectra of quadrupolar nuclei contained in stretched hydrogels. In each of these cases, experimental data were acquired, and methods were then developed to estimate model parameter values. Chapter 3 describes the NMR experiments that examined the chemical shift differences induced on 23Na+ by the SR, thulium 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrakis (methylenephosphonate), as functions of Na+ and other competing ions. We developed a mathematical model that successfully matched the experimental dependencies, and esti- mated various model parameters. In Chapter 4, we mathematically described the decay of magnetisation of hyperpolarised nuclei (achieved using DNP) as observed using 13C NMR spectroscopy. It was found that the longitudinal relaxation time constant, T1, estimated using a regularly timed pulse sequence was artefactually reduced. We proposed a irregu- larly timed pulse sequence, which enabled correct estimates of the longitudinal relaxation rate constant, T1, and α, the NMR pulse angle. This approach was applied to exper- imental sequences obtained on hyperpolarised 13C-urea, and parameter estimates were consistent with those independently obtained by an ‘inversion-recovery’ pulse sequence. Chapter 5 describes the application of Bayesian analysis and Markov chain Monte Carlo (MCMC) methods to estimate the myriad relaxation rate constants that describe the shape and features of the z-spectra of quadrupolar nuclei contained in stretched gels. This approach proved successful in obtaining model fits and parameter estimates to ex- perimental z-spectra of 23Na+ and 7Li+ in stretched hydrogels. iii Chapter 6 examines the stoichiometric relationship between the rate at which Na+ ions are transported across the RBC membrane by the NKA to its indirect consumption rate of glucose. We performed experimental NMR time courses on suspensions of RBCs, and determined that this stoichiometric ratio was close to that theoretically predicted. It was determined that the NKA was very efficient at consuming ATP and glucose, and not an explanation for “missing” ATP turnover in the RBC. Last, for Chapter 7 I explored the origin of CMF in human RBCs; this was done in two ways: (i) CMF was mathematically modelled as a constrained random walk (CRW); and (ii) experimental DIC recordings of RBC CMF were acquired in the presence of various effectors, and analysed using the CRW model. We found that the model had the frequency characteristics and stochastic behaviour seen with CMF. It was observed that effectors of the cytoskeleton and mem- brane flexibility could significantly affect the amplitude of CMF. Furthermore, we found that previous studies that claimed a dependence of CMF on ATP were misleading, as they ignored that the cytoskeleton was alkylated under the same experimental conditions used. Overall, this work ruled out a number of potential sources of ATP hydrolysis in the RBC, and provided several model frameworks that describe metabolic systems in the human RBC, and various NMR spectral characteristics. iv List of abbreviations ADP Adenosine diphosphate AMP Adenosine monophosphate ATP Adenosine triphosphate AR Autoregressive BPG Bisphosphoglycerate BSA Bovine serum albumin CMF Cell membrane flickering CRW Constrained random walk cs Capillary-sphere DIC Differential interference contrast DNP Dynamic nuclear polarisation DOTP 1,4,7,10-Tetraazacyclododecane-1,4,7,10-tetrakis (methylenephosphonate) FID Free induction decay GAPDH Glyceraldehyde-3-phosphate dehydrogenase GrnP(h) Dihydroxyacetone-phosphate hydrate HEPES 4-(2-Hydroxyethyl)-1-piperazineethanesulfonic acid HP Hyperpolarised Ht Haematocrit MCMC Markov chain Monte Carlo MRI Magnetic resonance imaging NEM n-Ethylmaleimide NKA Na+,K+-ATPase NMR Nuclear magnetic resonance OA Okadaic acid PBS Phosphate buffered saline PDAc Phorbol 12,13-diacetate Pi Inorganic phosphate PKC Protein kinase C v PPP Tripolyphosphate RBC Red blood cell RF Radiofrequency Rib5P Ribose 5-phosphate RMSD Root mean square displacement Ru5P Ribulose 5-phosphate RW Random walk SR Shift reagent vi Contents 1 Introduction 1 1.1 Motivation . .1 1.2 Aims . .2 2 Theory of Methods 4 2.1 NMR spectroscopy . .4 2.1.1 RBC preparation for NMR spectroscopy . .7 2.1.2 Shift reagents . .8 2.1.3 Hyperpolarised NMR . .9 2.1.4 z-Spectra . 12 2.2 Microscopy . 15 2.2.1 Phase contrast microscopy . 15 2.2.2 DIC microscopy . 16 2.2.3 RBC morphology . 16 2.3 Deduction and logic . 20 2.3.1 Probability theory . 20 2.3.2 Practical Bayesian analysis . 22 2.3.3 MCMC sampling . 27 3 Shift Reagents 30 3.1 Introduction . 30 vii 3.2 Paper I: Quantitative model of NMR chemical shifts of 23Na+ induced by TmDOTP: applications in studies of Na+ transport in human erythrocytes 32 Supporting material . 43 4 Hyperpolarised NMR Spectroscopy 52 4.1 Introduction . 52 4.2 Paper II: Simultaneous estimation of T1 and the flip angle in hyperpolarized NMR experiments using acquisition at non-regular time intervals . 54 5 z -Spectra 61 5.1 Introduction . 61 5.1.1 Quantum mechanical description . 62 5.1.2 Approach to parameter estimation . 64 5.2 Paper III: Relaxation times of spin states of all ranks and orders of quadrupo- lar nuclei estimated from NMR z-spectra: Markov chain Monte Carlo anal- ysis applied to 7Li+ and 23Na+ stretched hydrogels . 70 5.3 Paper IV: 7Li+ NMR quadrupolar splitting in stretched hydrogels: devel- opments in relaxation time estimation from z-spectra . 80 5.4 133Cs+ z-spectra . 86 6 Na+,K+-ATPase & Glycolysis Coupling 88 6.1 Introduction . 88 6.2 Paper V: Stoichiometric relationship between Na+ ions transported and glucose consumed in human erythrocytes: Bayesian analysis of 23Na and 13C NMR time course data . 90 Supporting material . 100 7 Cell Membrane Flickering 105 7.1 Introduction . 105 7.2 Paper VI: Membrane flickering of the human erythrocyte: described by a constrained random walk . 108 viii Supporting Material . 131 7.3 Paper VII: Membrane flickering of the human erythrocyte: Physical and chemical effectors . 136 Supporting Material . 154 8 Overview 162 8.1 Introduction . 162 8.2 Summary of finding . 162 8.3 Future directions . 164 8.3.1 HP studies of RBCs . 164 8.3.2 z-spectra . 164 8.3.3 ATP consumption in the RBC . 165 Bibliography 173 ix Chapter 1 Introduction 1.1 Motivation The human erythrocyte or red blood cell (RBC) is a relatively simple cell despite its impor- tant function of oxygen distribution to a wide range of tissues.
Load more

Recommended publications
  • Golden Yearbook
    Golden Yearbook Golden Yearbook Stories from graduates of the 1930s to the 1960s Foreword from the Vice-Chancellor and Principal ���������������������������������������������������������5 Message from the Chancellor ��������������������������������7 — Timeline of significant events at the University of Sydney �������������������������������������8 — The 1930s The Great Depression ������������������������������������������ 13 Graduates of the 1930s ���������������������������������������� 14 — The 1940s Australia at war ��������������������������������������������������� 21 Graduates of the 1940s ����������������������������������������22 — The 1950s Populate or perish ���������������������������������������������� 47 Graduates of the 1950s ����������������������������������������48 — The 1960s Activism and protest ������������������������������������������155 Graduates of the 1960s ���������������������������������������156 — What will tomorrow bring? ��������������������������������� 247 The University of Sydney today ���������������������������248 — Index ����������������������������������������������������������������250 Glossary ����������������������������������������������������������� 252 Produced by Marketing and Communications, the University of Sydney, December 2016. Disclaimer: The content of this publication includes edited versions of original contributions by University of Sydney alumni and relevant associated content produced by the University. The views and opinions expressed are those of the alumni contributors and do
    [Show full text]
  • FROM the DIRECTOR: OUR NUMBERS ARE up in This Issue: Scientists Are Accustomed to Dealing with Some Pretty Big Numbers – and Some Very Small Ones Too
    Australian Synchrotron Lightspeed: November 2008 FROM THE DIRECTOR: OUR NUMBERS ARE UP In this issue: Scientists are accustomed to dealing with some pretty big numbers – and some very small ones too. • From the Director • A Tribute to Hans Freeman Take an electron, for example. It weighs around • Up to Speed • Beamtime Applications 9.10938188 x 10‐31 kilograms when it’s just sitting • Synchrotron opens up around. Now take a few more, turn them into a • In science, a lot can happen in one night beam 0.06 millimetres wide, and accelerate the • Experimenting with SAXS beam to say 99.9987% of the speed of light, which • One in a thousand is 299,792,458 metres per second. Then persuade • The next generation of synchrotron PhDs your electron beam to turn enough corners to keep • Another high-performance it circulating in a synchrotron storage ring 24 hours machine • Beamline Focus a day. • Rapid Access on Trial • New Survey to Boost User That’s the amazing feat regularly performed by the Satisfaction Australia Synchrotron’s team of engineers, • A traveller’s tale accelerator physicists, operators, technicians and • Events Diary • Careers at The Australian Prof. Robert Lamb other support staff. Impressed? I certainly am. Especially when that’s combined with a beam availability of 98.3 per cent that puts us in the world’s top five synchrotrons in terms of performance. And it seems our users are impressed too. Since we opened in July 2007, over 500 users have collectively visited us more than 1000 times, and we were only running at 30 per cent capacity.
    [Show full text]
  • 9781920898359 Appendices R
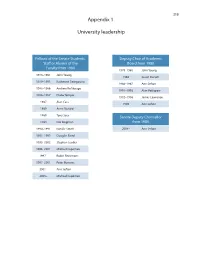
    319 Appendix 1 University leadership Fellows of the Senate Students, Deputy Chair of Academic Staff or Alumni of the Board from 1980 Faculty from 1980 1978–1980 John Young 1978–1981 John Young 1986 Susan Dorsch 1979–1993 Katherine Georgouras 1986–1987 Ann Sefton 1983–1986 Andrew Refshauge 1991–1993 Alan Pettigrew 1986–1987 Diana Temple 1992–1996 James Lawrence 1987 Alan Cass 1996 Ann Sefton 1989 Anna Donald 1989 Tony Sara Senate Deputy Chancellor 1989 Eric Wegman from 1980 1990–1991 Natalie Smith 2004– Ann Sefton 1993–1995 Douglas Baird 1995–2002 Stephen Leeder 1996–2001 Michael Copeman 1997– Robin Fitzsimons 1997–2001 Peter Burrows 2001– Ann Sefton 2005– Michael Copeman 320 Appendix 2 Deans of the Faculty of Medicine from 1980 1974 –1989 Richard S Gye 1989 –1996 John Atherton Young 1997–2002 Stephen Leeder 2003 – Andrew Coats Appendix 3 Current Emeritus Professors Barry Baker John Little Tony Basten William McCarthy Geoffrey Berry James McLeod Charles Blackburn Russell Meares Charles Bridges-Webb Gerald Milton Neil Buchanan Kim Oates Peter Castaldi Murray Pheils John Chalmers Wai-On Phoon Patrick De Burgh Thomas Reeve Susan Dorsch Douglas Saunders Hans Freeman Ann Sefton Kerry Goulston Ainslie Sheil Richard Gye Frederick Stephens Akos Gyory Michael Taylor Noel Hush Thomas Taylor Gordon Johnson Stewart Truswell Charles Kerr John Turtle James Lawrence Robert Wake 321 Appendix 4 Professors appointed or promoted 1980–2005 1980 W Cramond 1989 Nicholas Hunt 1994 Leigh Delbridge 1980 Graeme Johnston 1989 John Sutton 1994 Ian Frazer 1980 Philip
    [Show full text]
  • Print This Article
    Liversidge Research Lecture No. 21 1978 ELEGANCE IN MOLECULAR DESIGN: THE COPPER SITE OF PHOTOSYNTHETIC ELECTRON-TRANSFER PROTEIN HANS C. FREEMAN The Royal Society of New South Wales Liversidge Research Lecture No. 21, 1978 Royal Society of NSW 1 Hans Charles Freeman This photograph is reproduced by permission of the Australian Journal of Chemistry and the RACI 472 2 Royal Society of NSW Liversidge Research Lecture No. 21, 1978 Liversidge Research Lecturer No. 21, 1978. HANS CHARLES FREEMAN 1929-2008 Hans Charles Freeman was born on 26 May 1929 in Breslau, Germany. His family arrived in Sydney as refugees in 1938. After attending Double Bay Public School, he received his secondary education at Sydney Boys' High School where he was taught science by the ‘now-legendary’ teacher Leonard A. Basser. He proceeded to the University of Sydney, graduating B.Sc.(1st. Class Hons.), with the University Medal in 1950. While holding appointments as Teaching Fellow and Temporary Lecturer, he carried out research on the dipole moments of organic molecules in the gas state under the supervision of Professor R.J.W. Le Fèvre, and graduated M.Sc. in 1952. In 1952-3 he was a Rotary Foundation Fellow at the California Institute of Technology. There, at the suggestion of Linus Pauling, he began research in X-ray crystal structure analysis with one of the leading thinkers and strategists of the subject, Edward W. Hughes. In 1954 he returned to the University of Sydney as a Lecturer in Chemistry, and completion of the research begun in California led to the award of a Sydney Ph.D.
    [Show full text]
  • Structural Approaches to Probing Metal Interaction with Proteins
    Journal of Inorganic Biochemistry 115 (2012) 138–147 Contents lists available at SciVerse ScienceDirect Journal of Inorganic Biochemistry journal homepage: www.elsevier.com/locate/jinorgbio Structural approaches to probing metal interaction with proteins Lorien J. Parker a,1,2, David B. Ascher a,2, Chen Gao a,2, Luke A. Miles a,b,c,3, Hugh H. Harris d,3, Michael W. Parker a,c,⁎,3 a Biota Structural Biology Laboratory, St. Vincent's Institute of Medical Research, 9 Princes Street, Fitzroy, Victoria 3065, Australia b Department of Chemical and Biomolecular Engineering, The University of Melbourne, Victoria 3010, Australia c Department of Biochemistry and Molecular Biology, Bio21 Molecular Science and Biotechnology Institute, The University of Melbourne, 30 Flemington Road, Parkville, Victoria 3010, Australia d School of Chemistry and Physics, University of Adelaide, South Australia 5005, Australia article info abstract Article history: In this mini-review we focus on metal interactions with proteins with a particular emphasis on the evident Received 1 December 2011 synergism between different biophysical approaches toward understanding metallobiology. We highlight Received in revised form 2 February 2012 three recent examples from our own laboratory. Firstly, we describe metallodrug interactions with glutathi- Accepted 20 February 2012 one S-transferases, an enzyme family known to attack commonly used anti-cancer drugs. We then describe a Available online 3 March 2012 protein target for memory enhancing drugs called insulin-regulated aminopeptidase in which zinc plays a role in catalysis and regulation. Finally we describe our studies on a protein, amyloid precursor protein, Keywords: Amyloid precursor protein that appears to play a central role in Alzheimer's disease.
    [Show full text]
  • V 27 No 1 March 2013
    II RR PP SS BULLETIN Newsletter of the International Radiation Physics Society Vol 27 No 1 March, 2013 One is constantly amazed at the exotic applications and breadth of physical insight that continues to spring from “old fashioned” x-ray spectroscopy. The choice of the cover art for this issue was inspired by a recent report in Nature* on the first determination of the spin rate of a supermassive black hole; and it is 84% as fast as Einstein's theory of gravity will allow. This required combining measurements from two x-ray spectroscopic space observatories, NASA's Nuclear Spectroscopic Telescope Array (NuSTAR) and the European Space Agency's XMM-Newton, in this instance both focused upon a galaxy-centered black hole (NGC1365) that has a mass 2 million times that of our sun and is 56 million light years distant. This required assessing both the higher energy continuum portion of spectra (10 keV to 30 keV from NuSTAR) as well as the broadened x-ray emission lines from neutral and partially ionized iron (XMM-Newton), interpreted as fluorescence produced by the reflection of hard X-rays (from the relativistic jet) off the inner edge of an accretion disk. The line broadening occurs from Doppler broadening, gravitational red shifting, and “blue shifting” from partially ionized Fe. *A rapidly spinning supermassive black hole at the centre of NGC1365, G. Risaliti et al., Nature 494 (2013) pp. 449-451. IRPS COUNCIL 2012 - 2015 President : Ladislav Musilek (Czech Republic) Vice Presidents : EDITORIAL BOARD Africa and Middle East : M.A. Gomaa (Egypt) Editors Western Europe : J.
    [Show full text]
  • Curriculum Vitae of Kyle M
    Curriculum Vitae of Kyle M. Lancaster, Ph.D. Cornell University Department of Chemistry and Chemical Biology Baker Laboratory, Ithaca, NY 14853 Office: 607-255-0502 • Email: [email protected] • Website: lancaster.chem.cornell.edu Appointments Cornell University, Department of Chemistry and Chemical Biology (CCB) Ithaca, NY Associate Professor of Inorganic Chemistry July 1st, 2018–Present Assistant Professor of Inorganic Chemistry July 1st, 2012–June 30th, 2018 Postdoctoral Associate (supervised by Serena DeBeer) and Visiting Lecturer 2010–2012 Education California Institute of Technology Pasadena,CA Ph.D., Chemistry (supervised by Harry B. Gray and John H. Richards) October 1, 2010 “Outer-Sphere Effects on the Copper Sites of Pseudomonas aeruginosa Azurins.” Pomona College Claremont, CA B.A., Molecular Biology with Distinction, magna cum laude May 15, 2005 “Mechanistic Swing” Honors and Awards National Fresenius Award – Phi Lambda Upsilon 2020 Kavli Fellow – National Academy of Sciences 2018 Dreyfus Foundation Postdoctoral Program in Environmental Chemistry Mentor 2018 Paul Saltman Award (Gordon Research Conferences, Metals in Biology) 2018 Alfred P. Sloan Research Fellowship 2017 National Science Foundation CAREER Award 2015 Department of Energy Office of Science Early Career Award 2015 Forbes 30 Under 30: Science and Health 2013 John Stauffer Scholarship for Academic Merit (Pomona College) 2005 Walter Bertsch Prize in Molecular Biology (Pomona College) 2005 NSF Graduate Research Fellowship 2005 Phi Beta Kappa 2005 Barry Goldwater Scholarship
    [Show full text]
  • Professor Peter Malcolm Colman
    Professor Peter Malcolm Colman The degree of Doctor of Science (honoris causa) was conferred upon Professor Peter Malcolm Colman at the ceremony held on 21 March 2000. Citation Chancellor, I have the honour to present to you Peter Malcolm Colman, for admission to the degree of Doctor of Science, honoris causa. Peter Malcolm Colman is a graduate of the University of Adelaide, from where he also obtained his doctorate in 1968. His thesis dealt with the determination of the structures of small molecules by X-ray diffraction. After three years as a postdoctoral fellow at the University of Oregon with Professor Brian Matthews, Colman took up another post-doctoral Research Fellowship, this time at the Max-Planck Institut in Munich. The research director was Professor Robert Huber (later a Nobel Laureate), who offered Colman a most challenging problem: the first crystal structure analysis of a complete antibody molecule. Colman's success in meeting that challenge firmly placed him in the ranks of the world's outstanding young protein crystallographers. Colman returned to Australia in 1975 as a Queen Elizabeth II Fellow at the School of Chemistry of the University of Sydney, in Professor Hans Freeman's crystallography laboratory. It was in Sydney that Colman began - out of curiosity - the study of an enzyme, neuraminidase - research which would later have far- reaching effects. In 1978, Colman was appointed to a research position at the CSIRO Division of Protein Chemistry at Parkville in Melbourne where he rose steadily through the ranks until he was Chief of the re-named CSIRO Division of Biomolecular Engineering, and later Director of the Biomolecular Research Institute, which is his current title.
    [Show full text]
  • Physical Inorganic Chemistry: Principles, Methods, and Reactions
    www.jamshimi.ir www.jamshimi.ir www.jamshimi.ir PHYSICAL INORGANIC CHEMISTRY www.jamshimi.ir www.jamshimi.ir PHYSICAL INORGANIC CHEMISTRY Principles, Methods, and Models Edited by Andreja Bakac www.jamshimi.ir Copyright Ó 2010 by John Wiley & Sons, Inc. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey Published simultaneously in Canada No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 kver Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation.
    [Show full text]
  • Faculty of Science Handbook 1996
    The University of Sydney Faculty of Science Handbook 1996 Editor Robert Kt Norris The Editor gratefully acknowledges the substantial inputs to the preparation of the Handbook by Ms Christine Hermely and Ms Danielle Heilpern from the Faculty of Science Office. The Editor also thanks all Departmental and School Faculty Handbook Liaison Officers for their assistance. Faculty of Science Handbook 1996 ©The University of Sydney 1995 ISSN 1034-2699 The University of Sydney N.S.W. 2006 Telephone (02) 351 2222 Faculty of Science Telephone (02) 351 3021 Faculty of Science Facsimile (02) 351 4846 Semester and vacation dates 1996 Semester Day 1996 First Semester and lectures begin Monday 26 February Easter recess Last day of lectures Friday 5 April Lectures resume Monday 15 April Study vacation—1 week beginning Monday 10 June Examinations commence Monday 17 June Second Semester and lectures begin Monday 22 July Mid-semester recess Last day of lectures Friday 27 September Lectures resume Monday 7 October Study vacation—1 week beginning Monday 4 November Examinations commence Monday 11 November • Set in 10 on 11.5 point Palatine Produced by the Publications Unit, The University of Sydney and printed in Australia by Ligare Pty Ltd, Riverwood, N.S.W. Text printed on 80gsm bond, recycled from milk cartons. Introduction iv Psychology 138 Message from the Dean V BSc (Advanced) degree program 140 BSc (Environmental) degree program 140 1. Staff 1 BSc (Molecular Biology and Genetics) degree program 141 2. Courses in the Faculty of Science 13 BSc/LLB 141 Departmental and Faculty advisers 17 Degree of Bachelor of Computer Science and Technology 142 3.
    [Show full text]
  • Honours Student's Presentation Evening RACI
    Dear NSW RACI readers Below are this week’s announcements from the RACI NSW Branch, a summary is given and then scroll down for the full text. RACI (NSW) Analytical Chemistry Group - Honours Student’s Presentation Evening When: Wednesday, 19th November 2008, 5.30 pm for 6.00 pm (The NSW RACI Branch will be putting on Wine, and Cheese from 5.30pm at the event) Where: University of Technology Sydney (Room 2.33, Building 4; officially labelled as CB04.02.33) Cost: FREE Full details see page 3 RACI Wall Planner 2009 Attention all Members – the 2009 Wall planner to be distributed in January 2009 is in the final stages of editing The coordinator hopes that the 2009 wall planner will be as accurate and as useful as possible - therefore she needs your help! Full details see page 4 Vale Hans Freeman Dear Colleagues, It is my sad duty to pass on to you all the news that Hans Freeman passed away. Full details see page 4 RACI NSW One-Day Organic Chemistry Symposium 2008 3rd December, School of Chemistry, The University of Sydney – See page 5 for the full program of talks. If you would like to register please email [email protected] The 2009 Honours prize (RACI Western Sydney Section) will be awarded for the best Honours thesis produced in 2008 by a student who is resident and/or has studied or undertaken research in western Sydney throughout the year. The RACI Western Sydney Section Honours Prize is now open Full details see page 6 An Invitation The Royal Australian Chemical Institute (NSW Branch) in conjunction with The Dairy Industry Association
    [Show full text]
  • ACA 2009 Buerger Award Symposium Bruker AXS
    American Crystallographic Association Number 4 Winter 2008 ACA 2009 Buerger Award Symposium Bruker AXS TRIUMPH MONOCHROMATOR Triple Your Intensity for Mo Kα ■ Curved crystal technology delivers three times the intensity of a conventional graphite monochromator for Mo Kα ■ Accelerates data collection ■ Delivers superior data from the most challenging samples ■ Compatible with all KAPPA APEX II systems www.bruker-axs.com s 1-800-234-XRAY s [email protected] think forward Crystallography American Crystallographic Association www.AmerCrystalAssn.org Table of Contents 2-3 President’s Column 3-4 News from Canada 5-8 Elizabeth Wood - ACA - March 1975 4-6 AIP Governing Board Meeting 10-11 Lyle Jensen (1915-2008) 11-12 Hans Freeman (1929-2008) 13 John Dimarco (1963-2008) Index of Advertisers 13-14 New IUCr Commission on Art and Science 16 Knoxville Memories 17-19 2009 ACA Election Results 20 ACA Corporate Members 20-26 2008 ACA Travel Award Winners 26-32 2008 USNCCr Travel Award Winners 32-34 USNCCr Report on the IUCr Congress 34 Senate Economic Stimulus 35 Martin Buerge Award to Mike James 36 B. E. Warren Award to Shin-Lin Chang Harvey Prize to David Eisenberg 38-39 Contributors to ACA Award Funds 40-42 ACA 2009 Toronto, Ontario -Preview 43 Future Meetings ACA 2009 Small Molecule Course 44 2009 Art in Crystallography Prize Calls for ACA Nominations Travel Funds Available What's on the Cover Contributors to this Issue Contributions toACA RefleXions may be sent to either of the Editors: Please address matters pertaining to advertisements, membership inquiries, or use of the ACA mailing list to: Connie (Chidester) Rajnak .......................Judith L.
    [Show full text]