DOCSLIB.ORG

Ring Current -Atmosphere Interactions Model with Stormtime Magnetic Field

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ring Current -Atmosphere Interactions Model with Stormtime Magnetic Field University of New Hampshire University of New Hampshire Scholars' Repository Doctoral Dissertations Student Scholarship Fall 2007 Ring current -atmosphere interactions model with stormtime magnetic field Alexander Emilov Vapirev University of New Hampshire, Durham Follow this and additional works at: https://scholars.unh.edu/dissertation Recommended Citation Vapirev, Alexander Emilov, "Ring current -atmosphere interactions model with stormtime magnetic field" (2007). Doctoral Dissertations. 406. https://scholars.unh.edu/dissertation/406 This Dissertation is brought to you for free and open access by the Student Scholarship at University of New Hampshire Scholars' Repository. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of University of New Hampshire Scholars' Repository. For more information, please contact [email protected]. R i n g C u r r e n t - A t m o s p h e r e I nteractions M o d e l W i t h S t o r m t i m e M a g n e t i c F i e l d b y ALEXANDER EMILOV VAPIREV M.S., Sofia University, Sofia, Bulgaria, 1999 DISSERTATION Submitted to the University of New Hampshire in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Physics September 2007 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. UMI Number: 3277150 INFORMATION TO USERS The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleed-through, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. ® UMI UMI Microform 3277150 Copyright 2007 by ProQuest Information and Learning Company. All rights reserved. This microform edition is protected against unauthorized copying under Title 17, United States Code. ProQuest Information and Learning Company 300 North Zeeb Road P.O. Box 1346 Ann Arbor, Ml 48106-1346 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. This dissertation has been examined and approved. \ J . ) . Dissertation Director, Vania K. Jordanova, Adjunct Re­ search Associate Professor of Physics Professo of PhysicsRoy Torbe: Professo of PhysicsRoy Joachim Reeder, Associate Professor of Physics Lynn Kistler, Associate Professor of Physics Jochen Heisenberg, Professor of Physics Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. D e d ic a t io n To my parents ”An expert is a man who has made all the mistakes which can be made in a very narrow field. ” - Niels Bohr iii Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. A cknowledgments I thank my academic adviser Prof. Vania Jordanova for giving me the opportunity to work with her. I thank her for her guidance throughout my research and studies. It has been a privilege to work with her. I thank the members of my dissertation committee for their time and patience and their useful suggestions and helpful comments. I want to thank all my teachers and colleagues from the Bulgarian Academy of Sciences and the University of Sofia and especially those at the department of Nuclear Energy and Nuclear Technologies and the department of Quantum Electronics and Laser Technologies. I want to thank the academic program coordinators Katie Makem and Kathy Giberson for their help on so many occasions. I want to thank all my colleagues at UNH and especially Douglas Larson, Burgin Donmez and Georgi Nenchev for all the help and conversations. I also want to thank Sorin Zaharia (LANL) and Yoshizumi Miyoshi (Nagoya University) for the useful discussions and support on numerous occasions. I want to express my sincere gratitude to Nikolay Tsyganenko (GSFC) and Reiner Friedel (LANL) for their help. I thank my parents, my brother, my sister and all my friends for their love and support through all these years. iv Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. C o n t e n t s D e d ic a t io n .............................................. iii A cknowledgments ..................................................................................................................................... iv L is t o f T a b l e s ............................................................................................................................................. v iii L is t o f F ig u r e s ......................................................................................................................................... ix A b s t r a c t ......................................................................................................................................................... x v ii 1 I ntroduction 1 2 O r ig in a n d D e v e l o p m e n t o f th e T e r r e s t r ia l R in g C u r r e n t 9 2.1 General Structure of the Ring C urrent ................................................................... 9 2.2 Measurements .............................................................................................................. 12 2.3 Sources of Ring Current Pa rtic le s ........................................................................... 16 2.3.1 The Solar W ind ........................................................................................... 18 2.3.2 The Ionosphere .............................................................................................. 19 2.3.3 Compositional C h a n g e s .............................................................................. 21 2.4 Ionospheric o u tflo w .................................................................................................... 23 2.5 Charge Exchange Losses........................................................................................... 26 2.5.1 Charge Exchange Processes....................................................................... 26 2.5.2 Energetic Neutral Atoms .......................................................................... 28 2.6 Coulomb C o llisio n s .................................................................................................... 29 2.7 Wave — Particle Interactions ................................................................................ 31 v Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. 3 T heoretical A pproach 44 3.1 Kinetic E q u a tio n ............................................................................................................. 44 3.2 Drifts of Ring Current Particles.................................................................................. 46 3.2.1 Radial and Azimuthal Drifts ........................................................................ 47 3.2.2 /ro — Drift............................................................................................................. 49 3.2.3 Energy Drift ....................................................................................................... 50 3.3 Charge Exchange Losses ................................................................................................ 50 3.4 Atmospheric Losses.......................................................................................................... 52 3.5 Ring Current Characteristics and Aeronomical E ffects ...................................... 53 3.6 Tsyganenko Magnetospheric Field Model .............................................................. 54 4 T he N umerical M odel 58 4.1 The Numerical Scheme of RAM .................................................................................. 58 4.1.1 Time splitting ................................................................................................... 58 4.1.2 High — Resolution Schemes............................................................................ 59 4.2 Bounce — Averaging along a Field L in e ................................................................. 60 4.3 Numerical Accuracy Tests of the Bounce — Averaging Technique .................. 62 4.4 Accuracy Tests for R A M ................................................................................................ 63 4.4.1 Equatorial Particle F lu x ..................... 64 4.4.2 Total Energy and Total Number of Particles.............................................. 65 5 M odel R esults 77 5.1 Observations .................................................................................................................... 77 5.1.1 Interplanetary D a ta ......................................................................................... 77 5.1.2 Magnetospheric Data ...................................................................................... 78 5.1.3 Input data for T04s m od el ............................................................................... 79 vi Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. 5.2 Bounce — Averaged Exospheric Hydrogen Density and Magnetic Gradient — Curvature Drift Velocity ........................................................................................... 79 5.3 Time Evolution of the Trapped Equatorial Flu x .................................................
Load more

Recommended publications
  • Sphere Confusion: a Textual Reconstruction of Instruments and Observational Practice in First-Millennium CE China Daniel Patrick Morgan
    Sphere confusion: a textual reconstruction of instruments and observational practice in first-millennium CE China Daniel Patrick Morgan To cite this version: Daniel Patrick Morgan. Sphere confusion: a textual reconstruction of instruments and observa- tional practice in first-millennium CE China . Centaurus, Wiley, 2016, 58 (1-2), pp.87-103. halshs- 01374805v3 HAL Id: halshs-01374805 https://halshs.archives-ouvertes.fr/halshs-01374805v3 Submitted on 4 Oct 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution - NonCommercial - ShareAlike| 4.0 International License Centaurus, 58.1 (2016) Sphere Confusion: a Textual Reconstruction of Astronomical Instruments and Observational Practice in First-millennium CE China * Daniel Patrick MORGAN Abstract: This article examines the case of an observational and demonstration- al armillary sphere confused, one for the other, by fifth-century historians of astronomy He Chengtian and Shen Yue. Seventh-century historian Li Chunfeng dismisses them as ignorant, supplying the reader with additional evidence. Using their respective histories and what sources for the history of early imperial ar- millary instruments survive independent thereof, this article tries to explain the mix-up by exploring the ambiguities of ‘observation’ (guan) as it was mediated through terminology, text, materiality and mathematics.
    [Show full text]
  • Abd Al-Rahman Al-Sufi and His Book of the Fixed Stars: a Journey of Re-Discovery
    ResearchOnline@JCU This file is part of the following reference: Hafez, Ihsan (2010) Abd al-Rahman al-Sufi and his book of the fixed stars: a journey of re-discovery. PhD thesis, James Cook University. Access to this file is available from: http://eprints.jcu.edu.au/28854/ The author has certified to JCU that they have made a reasonable effort to gain permission and acknowledge the owner of any third party copyright material included in this document. If you believe that this is not the case, please contact [email protected] and quote http://eprints.jcu.edu.au/28854/ 5.1 Extant Manuscripts of al-Ṣūfī’s Book Al-Ṣūfī’s ‘Book of the Fixed Stars’ dating from around A.D. 964, is one of the most important medieval Arabic treatises on astronomy. This major work contains an extensive star catalogue, which lists star co-ordinates and magnitude estimates, as well as detailed star charts. Other topics include descriptions of nebulae and Arabic folk astronomy. As I mentioned before, al-Ṣūfī’s work was first translated into Persian by al-Ṭūsī. It was also translated into Spanish in the 13th century during the reign of King Alfonso X. The introductory chapter of al-Ṣūfī’s work was first translated into French by J.J.A. Caussin de Parceval in 1831. However in 1874 it was entirely translated into French again by Hans Karl Frederik Schjellerup, whose work became the main reference used by most modern astronomical historians. In 1956 al-Ṣūfī’s Book of the fixed stars was printed in its original Arabic language in Hyderabad (India) by Dārat al-Ma‘aref al-‘Uthmānīa.
    [Show full text]
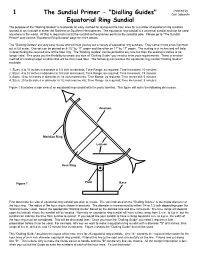
  • "Dialling Guides" Equatorial Ring Sundial
    created by 1 The Sundial Primer - "Dialling Guides" Carl Sabanski Equatorial Ring Sundial The purpose of the "Dialling Guides" is to provide an easy method for laying out the hour lines for a number of equatorial ring sundials located at any latitude in either the Northern or Southern Hemispheres. The equatorial ring sundial is a universal sundial and can be used anywhere in the world. All that is required is to tilt the sundial so the gnomon points to the celestial pole. Please go to "The Sundial Primer" and visit the "Equatorial Ring Sundial" page for more details. The "Dialling Guides" are very easy to use and will help you lay out a variety of equatorial ring sundials. They come in two sizes if printed out at full scale. One set can be printed on 8-1/2" by 11" paper and the other on 11" by 17" paper. The scaling is in inches and will help in determining the required size of the hour ring. The "Dialling Guides" can be printed to any size but then the scaling in inches is no longer valid. This gives you the flexibility to create any size of "Dialling Guide" you need to meet your requirements. There is another method of creating larger sundials that will be discussed later. The following summarizes the equatorial ring sundial "Dialling Guides" available: 1. Sizes: 4 to 10 inches in diameter in 1/4 inch increments; Time Range: as required; Time Increment: 10 minutes 2. Sizes: 4 to 10 inches in diameter in 1/4 inch increments; Time Range: as required; Time Increment: 15 minutes 3.
    [Show full text]
  • Armillary Sphere
    Armillary Sphere Inventory no. 45453 Armillary sphere Armillary sphere for demonstration of the heavenly spheres made and signed by Carlo Plato, Rome, c.1588. The armillary sphere is an instrument that extends right back to the ancients, and was certainly in used by the second-century astronomer and mathematician Claudius Ptolemy, of Alexandria. It was a mathematical instrument designed to demonstrate the movement of the celestial sphere about a stationary Earth at its centre. The concept of the celestial sphere was fundamental to astronomy from Antiquity through the Middle Ages and into the Early-Modern era. At the centre of the sphere is the Earth. As the Earth is stationary in this model, it is the celestial sphere which rotates about it and acts as a reference system for locating the celestial bodies – stars, in particular – from a geocentric perspective. The instrument survived throughout the medieval period into the early modern era, and in many respects came to symbolise the queen of the sciences, astronomy. It wasn’t until the middle of the sixteenth-century that the basis of the instrument – a geocentric concept of the Universe – was seriously challenged by the Polish mathematician, Nicolaus Copernicus. Even then, the instrument still continued to serve a useful purpose as a purely mathematical instrument. Portrait of Nicolas Copernicus 1580 Held stationary at the centre is a small brass sphere representing the Earth. About it rotate a set of rings representing the heavens – the celestial sphere – one complete revolution approximating to a day or 24 hours. The sphere is mounted at the celestial poles which define the axis of rotation, and its structure includes an equatorial ring and, parallel to this, above and below, two smaller rings representing the Tropic of Cancer to the north, and the Tropic of Capricorn to the south.
    [Show full text]
  • Climatic Effects of an Impact Induced Equatorial Debris Ring
    SAND2001-2464J Climatic Effects of an Impact Induced Equatorial Debris Ring Peter J. Fawcett’ Mark B.E. Boslough’ 1. University of New Mexico 220 Northrop Hall Albuquerque, NM 87131 2. Sandia National Laboratories Albuquerque, NM To be submitted to Journal of Geophysical Research, Atmospheres Abstract Several theoretical and laboratory studies suggest that some large impact events are capable of inserting material into space depending on mechanics of the impact. This material would quickly coalesce to form a temporary debris ring in orbit around the equator, which would cast its shadow on the winter hemisphere. The results of an atmospheric GCM simulation where an orbiting equatorial debris ring is applied as a boundary condition to the model show how the longer-term effects of a major impact could affect the climate system. The primary effect is a severe cooling in the tropics and the subtropics, especially under the seasonally migrating ring shadow. The globe cools and becomes drier, with the exception of monsoonal regions that become wetter. The Hadley Cell is weakened resulting in drier tropics and weaker subtropical high pressure cells in the winter hemisphere. Because the tropics cool more than middle latitude regions, the equator-to-pole temperature gradient becomes shallower resulting in weaker tropospheric winds and less high-latitude storminess. We suggest that the late Eocene impact(s) (35.5 Ma) could have generated a geologically temporary orbiting debris ring based on the global distribution of tektites associated with these events and patterns of climate change immediately above the iridiummicrotektite layer. The Cretaceous-Tertiary boundary event, while larger, did not produce a debris ring.
    [Show full text]
  • Magnetic Interconnection of Saturn's Polar Regions: Comparison of Modelling Results with Hubble Space Telescope UV Auroral
    EGU Journal Logos (RGB) Open Access Open Access Open Access Ann. Geophys., 31, 1447–1458, 2013 www.ann-geophys.net/31/1447/2013/ Advances in Annales Nonlinear Processes doi:10.5194/angeo-31-1447-2013 © Author(s) 2013. CC Attribution 3.0 License.Geosciences Geophysicae in Geophysics Open Access Open Access Natural Hazards Natural Hazards and Earth System and Earth System Sciences Sciences Magnetic interconnection of Saturn’s polar regions: comparisonDiscussions of Open Access Open Access modelling results with HubbleAtmospheric Space Telescope UV auroralAtmospheric images Chemistry Chemistry E. S. Belenkaya1, S. W. H. Cowley2, V. V. Kalegaevand Physics1, O. G. Barinov1, and W. O. Barinova1 and Physics 1 Lomonosov Moscow State University, Skobeltsyn Institute of Nuclear Physics, 1(2), Leninskie gory, GSP-1, MoscowDiscussions Open Access 119991, Russian Federation Open Access 2Department of Physics & Astronomy, UniversityAtmospheric of Leicester, Leicester LE1 7RH, UK Atmospheric Correspondence to: E. S. Belenkaya ([email protected])Measurement Measurement Techniques Techniques Received: 14 May 2013 – Revised: 15 July 2013 – Accepted: 16 July 2013 – Published: 28 August 2013 Discussions Open Access Open Access Abstract. We consider the magnetic interconnection of Sat- 1 Introduction Biogeosciences urn’s northern and southern polar regionsBiogeosciences controlled by the Discussions interplanetary magnetic field (IMF), studying in particular the more complex and interesting case of southward IMF, In this paper we study Saturn’s ultraviolet (UV) auroral emis- when the Kronian magnetospheric magnetic field structure sions observed by the Hubble Space Telescope (HST) in Open Access one hemisphere, and their mapping along field lines intoOpen Access is the most twisted. The simpler case of northward IMF is Climate also discussed.
    [Show full text]
  • Aristarchus' Derivation of the Sun's Distance
    A HISTORY OF ASTRONOMY APPENDICES present stabie atoms have been formed in long periods of development out of the original bulk of protons, the remainder of which appears in the spectra of the A-type stars, the prominences on the sun, and the APPENDIX A water on earth, the basic matter of all organisms, including ourselves- without water, no protoplasm and no life would have been possible. This means that in those cosmie furnaces-the central parts de ep in the ARISTARCHUS' DERIVATION OF THE stars-the entire world was, and still is, fabricated, the materials con- SUN'S DISTANCE stituting its matter as well as the radiations constituting its life. It is this life which appears, greatly weakened, at the hot stellar surfaces and, again a thousand times weakened, transformed into the life-energy of Aristarehus' seventh proposition is the most important, sinee it is there that living beings. the essential numerical result is derived. The demonstration is interesting Another difficulty arises: to penetrate into the heavier nuclei, hence enough, in .ts value to future astronomy, to reproduee it here in brief. In the to build the heavier atoms, theory may demand still greater densities figure Arepresents the position of the sun, B of the earth, C of the moon and greater veloeities of the protons, corresponding to still higher tem- when seen halved. Henee angle EBD=angle BAC=3°. Let the angle FBE( =45°) be biseeted by BG. Sinee the ratio ofa great and a small tangent peratures of hundreds or thousands of millions of degrees; these we do to a eircle is greater than the ratio of the underlying arcs and angles, the not find even in the steIlar interiors.
    [Show full text]
  • Jones Preprint Precision of Time Observation
    CHAPTER 1 PRECISION OF TIME OBSERVATION IN GRECO-ROMAN ASTROLOGY AND ASTRONOMY ALEXANDER JONES * PREPRINT, 2016 * Forthcoming in M. Morfouli and E. Nicolaidis, eds., Time Accuracy in Physics and Astronomy. Alexander Jones Page 1 7/13/19 Abstract This article reviews the evidence for the precision of observed (or allegedly observed) time determinations in the Greek astral sciences. In the practice of astrology, the determination of times—most commonly times of births—was the province of lay observers, and the precision was not normally more refined than to the seasonal hour. In astronomy, the extant observational records show a broad trend towards more refined precision, though the apparent culmination of this trend in Ptolemy is due not only to his employment of the armillary astrolabe as a precision time-telling instrument but also to his penchant for fabrication and tampering in his observation reports. Ptolemy's claims to have attained to unprecedented time precision in the observations on which his tables were ostensibly based likely contributed to their early and widespread adoption by astrologers. Introduction The practice of astrology was one of the most conspicuous points of contact between technical astronomy and the lay public in antiquity. The personal horoscope is the emblematic document of this contact. A client, who could be a person of practically any social status and who would likely be ignorant of all but the most obvious facts of astronomy, provided the astrologer with his or her date, time, and (if not local) place of birth, and the astrologer employed astronomical tables or almanacs to determine the celestial longitudes of the Sun, Moon and planets and the points of the ecliptic that were crossing the horizon and meridian planes at that time and place.
    [Show full text]
  • Astronomical Instruments with Two Scales Drawn on Their Common Circumference of Rings in the Joseon Dynasty
    Research Paper J. Astron. Space Sci. 34(1), 45-54 (2017) https://doi.org/10.5140/JASS.2017.34.1.45 Astronomical Instruments with Two Scales Drawn on Their Common Circumference of Rings in the Joseon Dynasty Byeong-Hee Mihn1,2†, Goeun Choi1,2, Yong Sam Lee3 1Korea Astronomy and Space Science Institute, Daejeon 34055, Korea 2Korea University of Science and Technology, Daejeon 34113, Korea 3Department of Astronomy and Space Science, Chungbuk National University, Cheongju 28644, Korea This study examines the scale unique instruments used for astronomical observation during the Joseon dynasty. The Small Simplified Armillary Sphere (小簡儀, So-ganui) and the Sun-and-Stars Time-Determining Instrument (日星定時儀, Ilseong-jeongsi-ui) are minimized astronomical instruments, which can be characterized, respectively, as an observational instrument and a clock, and were influenced by the Simplified Armilla (簡儀, Jianyi) of the Yuan dynasty. These two instruments were equipped with several rings, and the rings of one were similar both in size and in scale to those of the other. Using the classic method of drawing the scale on the circumference of a ring, we analyze the scales of the Small Simplified Armillary Sphere and the Sun-and-Stars Time-Determining Instrument. Like the scale feature of the Simplified Armilla, we find that these two instruments selected the specific circumference which can be drawn by two kinds of scales. If Joseon’s astronomical instruments is applied by the dual scale drawing on one circumference, we suggest that 3.14 was used as the ratio of the circumference of circle, not 3 like China, when the ring’s size was calculated in that time.
    [Show full text]
  • From the Scale Model of the Sky to the Armillary Sphere
    From the scale model of the sky to the armillary sphere Alejandro Gangui IAFE/Conicet and Universidad de Buenos Aires, Argentina. Roberto Casazza Universidad Nacional de Rosario and Universidad de Buenos Aires, Argentina. Carlos Paez Instituto Superior de Formación Docente N° 29, Merlo, Buenos Aires, Argentina. It is customary to employ a semi-spherical scale model to describe the apparent path of the Sun across the sky, whether it be its diurnal motion or its variation throughout the year. A flat surface and three bent semi-rigid wires (representing the three solar arcs during solstices and equinoxes) will do the job. On the other hand, since very early times, there have been famous armillary spheres built and employed by the most outstanding astronomers for the description of the celestial movements. In those instruments, many of them now considered true works of art, Earth lies in the center of the cosmos and the observer looks at the whole "from the outside". Of course, both devices, the scale model of the sky and the armillary sphere, serve to represent the movement of the Sun, and in this paper we propose to show their equivalence by a simple construction. Knowing the basics underlying the operation of the armillary sphere will give us confidence to use it as a teaching resource in school. PACS: 01.40.-d, 01.40.ek, 95.10.-a An ancient astronomical instrument In Latin, armilla means ring or bracelet. From this comes the name armillary sphere, used to designate a model or three-dimensional representation of the celestial sphere, the apparent path of the Sun in the sky and some significant astronomical elements such as the celestial equator, tropics, polar circles and the ecliptic.
    [Show full text]
  • Cosmographical Discussions in China from Early
    COSMOGRAPHICAL DISCUSSIONS IN CHINA FROM EARLY TIMES UP TO THE T1ANG DYNASTY by CHRISTOPHER CULLEN, M.A. (Oxon.) Thesis submitted for the degree of Ph.D. School of Oriental and African Studies, University of London. 1977. ProQuest Number: 10672707 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 10672707 Published by ProQuest LLC(2017). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 2 ABSTRACT Cosmography is the study of the shape, size, disposition and other properties of the large-scale com­ ponents of the physical universe. The following survey assembles and discusses available Chinese material on this subject from early times up to-the rise of the T ’ang dynasty in A.D, 6l8 , after which Chinese interest in the topic seems to have diminished. Part I discusses evidence front texts dating < before 250 B.C. A cosmography involving a number of mythical elements is thus reconstituted; heaven is a solid vault over a flat square earth. Geographical speculations about the existence of several continents are discussed. Part II describes the Kai t 1ien theory according to the Chou pei, a book possibly compiled in the first century B.C.; an umbrella-like heaven rotates over a similarly shaped earth.
    [Show full text]
  • 11 the PHYSICAL UNIVERSE of Dantel
    11 THE PHYSICAL UNIVERSE OF DANTEl is an inviting speculation as to what Dante Alighieri I’ would have been had he lived as a contemporary of ourselves. Removed from the sound of the monastery bells which ordered the days of the Middle Ages, and plunged into the bustle and clangor of our own time, would Dante still have become the Divine Poet? According to some, the question must be answered in the negative, and in this strain Grandgent speaks of the Middle Ages :2 “It is the age of religion. To theology the best intellects turned as instinctively as in our day they are drawn to high finance. Had the great business organizer who has recently passed away lived in the thirteenth century, he would natu- rally have been an ecclesiastic, an eminent theologian, a pillar of the Church; and St. Thomas, were he now alive, might well be a railway magnate.” In spite of the existence of great captains and great buca- neers without the Church, and courts bursting with the op- posing spirit, like that of Frederick 11, hardly any one will contradict the fundamental idea just expressed : that the 1The author takes this occasion to thank Professors Vito Volterra and G. Vacca, and Miss Luisa Socci, of Rome, Italy, as well as his father and Professor H. W. Tyler, of Boston, for assistance in the preparation of this lecture. Professor F. Cantelli, of Palermo, Sicily, very kindly sent copies of his own papers and those of Professor Angelitti, referred to below. Readers who find this subject interesting may pursue it further in the references given from time to time in the course of the lecture, and also in Dreyer, “Planetary Systems,” Cambridge, 1906, and Orr, “Dante and the Early Astronomers,” London, 1914.
    [Show full text]