DOCSLIB.ORG

Operator Algebras in Quantum Mechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Operator Algebras in Quantum Mechanics Operators and Operator Algebras in Quantum Mechanics Alexander Dzyubenko Department of Physics, California State University at Bakersfield Department of Physics, University at Buffalo, SUNY Supported in part by NSF Department of Mathematics, CSUB September 22, 2004 PDF created with pdfFactory Pro trial version www.pdffactory.com Outline v Quantum Harmonic Oscillator Ø Schrödinger Equation (SE) Ladder Operators Ø Coherent and Squeezed Oscillator States PDF created with pdfFactory Pro trial version www.pdffactory.com Classical Harmonic Oscillator Total Energy = Kinetic Energy + Potential Energy p2 mw 2 x2 H = K +V (x) = + 2m 2 Hamiltonian Function k Frequency m k 2p w = = m T Total Energy: E = mw2 A2 Period Amplitude PDF created with pdfFactory Pro trial version www.pdffactory.com Quantum Harmonic Oscillator Total Energy = Kinetic Energy + Potential Energy pˆ 2 mw2 xˆ2 Hˆ = Kˆ +Vˆ = + 2m 2 Probability Hamiltonian Operator: Acts on Wave Functions Y = Y(x,t) = x Y Density: 2 ¶ | Y(x,t) | Momentum Operator pˆ = -ih ¶x Coordinate Operator xˆ = x Time-Dependent SchroedingerEquation: ¶Y(x,t) ih = HˆY(x,t) ¶t PDF created with pdfFactory Pro trial version www.pdffactory.com Erwin Schrödinger Once at the end of a colloquium I heard Debye saying something like: “Schrödinger, you are not working right now on very important problems… why don’t you tell us some time about that thesis of de Broglie’s… In one of the next colloquia, Schrödinger gave a beautifully clear account of how de Broglie associated a wave with a particle, and how he could obtain the quantization rules… When he had finished, Debye casually remarked that he thought this way of talking was rather childish… To deal properly with waves, one had to have a wave equation. Felix Bloch Address to the American Physical Society, 1976 PDF created with pdfFactory Pro trial version www.pdffactory.com SE as an EigenvalueEquation Time-Dependent SchroedingerEquation (SE): ¶Y(x,t) ih = HˆY(x,t) = EY(x,t) ¶t E Energy Y(x,t) = j(x)exp(-i t) := j(x)exp(-iwt) EigenvalueE h Time-Independent SE: Hˆj(x) = Ej(x) h2 d 2j mw2 x2 For a Harmonic Oscillator: - + j = Ej 2m dx2 2 PDF created with pdfFactory Pro trial version www.pdffactory.com SE for Quantum Harmonic Oscillator d 2j 2m æ mw2 x2 ö + ç E - ÷j = 0 - ¥ < x < +¥ 2 2 ç ÷ dx h è 2 ø • A well-known equation in mathematics • Solutions were explored by Charles Hermite(1822-1901) PDF created with pdfFactory Pro trial version www.pdffactory.com Requirements for a Solution Physically reasonable wave functions must drop to zero for | x |® ¥ Symmetry of the potential => even and odd solutions Potential Barrier Discrete Energy EigenvaluesEn QM: Eigenfunctions: are only allowed Penetration QM Wavefunctions “Below the Barrier” PDF created with pdfFactory Pro trial version www.pdffactory.com (Quantum) Operator Approach: Non-Commutativity, Ladder Operators, … PDF created with pdfFactory Pro trial version www.pdffactory.com Non-Commutative Algebras ¶ Momentum Operator pˆ = -ih ¶x Coordinate Operator xˆ = x Commutator: [ pˆ, xˆ] = pˆxˆ - xˆpˆ = -ih d df [ pˆ, xˆ] f = -ih ( fx) + ih x = -ihf " f (x) dx dx Non-Commutativity=> Heisenberg Uncertainty Principle PDF created with pdfFactory Pro trial version www.pdffactory.com Hermitianand Unitary Operators HermitianConjugates: * y Aˆ j = ( j Aˆ + y ) or, incoordinate representation, * ò dxy (x)* Aˆ(x)j(x) = (ò dxj(x)* Aˆ + (x)y (x)) HermitianOperators: Unitary Operators: ˆ ˆ + A = A Uˆ + = Uˆ -1 Real Eigenvalues Describe Time Evolution in QM Complete Set of Eigenstates Perform Operator Transformations Physical Observables in QM are Aˆ ® Bˆ = UˆAˆUˆ + described by HermitianOperators PDF created with pdfFactory Pro trial version www.pdffactory.com Heisenberg Uncertainty Principle Non-Commutativity: [ pˆ, xˆ] = pˆxˆ - xˆpˆ = -ih Heisenberg Uncertainty Principle: Dp × Dx ³ h / 2 2 DA = Aˆ 2 - Aˆ Aˆ = j Aˆ j = ò dxj(x)* Aˆ(x)j(x) Uncertainty= Mean Square Deviation Expectation Value of A = Sqrt[Variance] Physical Observable A => Hermitian(self-adjoint) operator Aˆ PDF created with pdfFactory Pro trial version www.pdffactory.com Non-Commutative Ladder Operators mw Xˆ = xˆ = X h Dimensionless [Pˆ, Xˆ ] = -i Operators pˆ d Pˆ = = -i mwh dX Ladder Operators Non-commutative 1 1 æ d ö a = (Xˆ + iPˆ )= ç X + ÷ algebra: 2 2 è dX ø + + 1 1 æ d ö [a,a ] = 1 a = (Xˆ - iPˆ)= ç X - ÷ 2 2 è dX ø PDF created with pdfFactory Pro trial version www.pdffactory.com Hamiltonian and Ladder Operators pˆ 2 mw2 xˆ 2 Hˆ = + = hw(a+a + 1 ) 2m 2 2 algebra: [a,a + ] = 1 Lowering Raising a 0 = 0 Coordinate Representation: X 0 = exp(- 1 X 2 ) Vacuum State 2 1 æ d ö a = ç X + ÷ Gaussian 2 è dX ø PDF created with pdfFactory Pro trial version www.pdffactory.com (Bose) Ladder Operators 1 n n = (a+ ) 0 n! Excited States n = 1, 2, 3, … + algebra Raising a n = n +1 n +1 => [a,a+ ] = 1 Lowering a n = n n -1 + Particle Number Operator a a n = n n PDF created with pdfFactory Pro trial version www.pdffactory.com Hamiltonian, Ladder Operators, Eigenstates Equidistant Energy Levels Probability Distributions + ˆ 1 1 + n H = hw(a a + 2 ) n = (a ) 0 n! Hamiltonian (Energy Operator) n = 0, 1, 2, … http://vega.fjfi.cvut.cz/docs/pvok/aplety/kv_osc/index.html PDF created with pdfFactory Pro trial version www.pdffactory.com Oscillator Eigenstates: ProbabiltyDistribution http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/ PDF created with pdfFactory Pro trial version www.pdffactory.com Oscillator Coherent States Displacement Operator Dˆ (a) = exp(aa + -a *a) Complex number Unitary ˆ Schrödinger 1927 Coherent States a = D(a) 0 (in a different form) Minimum Behave Uncertainty Dp × Dx = h / 2 “most classically” States ¥ n 1 2 a a = exp(- 2 |a | )å n n=0 n! PDF created with pdfFactory Pro trial version www.pdffactory.com Disentangling the Operators ˆ + * Displacement D(a) = exp(aa -a a) = Operator 1 2 + * = exp(- 2 |a | )exp(aa )exp(-a a) Baker-Campbell- Algebra + Hausdorfformula Used: [a,a ] = 1 Coherent States a = Dˆ (a) 0 Superposition of an infinite # of oscillator ¥ a n states |n> with proper 1 2 amplitudes and phases a = exp(- 2 |a | )å n n=0 n! PDF created with pdfFactory Pro trial version www.pdffactory.com Displacement Operator Dˆ + (a)a+ Dˆ (a) = a+ + a Dˆ (a) = exp(aa+ -a *a) Dˆ + (a)aDˆ (a) = a + a * Generates an d Rea d Ima Overcomplete Set a a = 1ˆ of Coherent States ò p Very useful in Quantum Optics ˆ and Field Theory a = D(a) 0 PDF created with pdfFactory Pro trial version www.pdffactory.com Squeezing Operator 2 ˆ 1 + 1 * 2 Unitary S(b ) = exp(2 ba - 2 b a ) Mixes Creation and Annihilation Operators: Sˆ + (b )a +Sˆ(b ) = cosh(b )a + - sinh(b )a Sˆ + (b )a Sˆ(b ) = cosh(b )a - sinh(b )a+ Generates Squeezed States: b = Sˆ(b ) 0 Minimum Uncertainty States + One coordinate uncertainty E.g., ∆x can be made arbitrarily small (squeezed) at the expense of ∆p. Reduction of Quantum Noise PDF created with pdfFactory Pro trial version www.pdffactory.com Bose and Fermi Statisics Bose-Einstein Statistics: + + + Commutation Relation [a,a ] = aa - a a = 1 Bosons: photons, phonons, … Squeezed States: Theory of Superfluidity Fermi-DiracStatistics: + + + AntiCommutation {a,a } = aa + a a = 1 Relation Fermions: electrons, protons, … Squeezed States: Theory of Superconductivity PDF created with pdfFactory Pro trial version www.pdffactory.com How successful is quantum mechanics? It works nicely and not just for tiny particles QM explains Macroscopic Quantum Phenomena: Superconductivity, Superfluidity, Josephson Effect, and the Quantum Hall Effect QM is crucial to explain how the Universe formed QM “explains” the stability of matter No deviations from quantum mechanics are known A HUGE problem: to describe gravitation in the framework of quantum mechanics “Theory of everything” will be a relativistic quantum-mechanical theory PDF created with pdfFactory Pro trial version www.pdffactory.com.
Load more

Recommended publications
  • Physics Study Sheet for Math Pre-Test
    AP Physics 1 Summer Assignments Dear AP Physics 1 Student, kudos to you for taking on the challenge of AP Physics! Attached you will find some physics-related math to work through before the first day of school. The problems require you to apply math concepts that were covered in algebra and trigonometry. Bring your completed sheets on the first day of school. Please familiarize yourself with the following websites. https://phet.colorado.edu/en/simulations/category/physics We will use this website extensively for physics simulations. These websites are good resources for physics concepts: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html http://www.thephysicsaviary.com/APReview.html http://www.physicsclassroom.com/ http://www.learnapphysics.com/apphysics1and2/index.html https://openstax.org/subjects/science This website provides free online textbooks with links to online simulations. Finally, you will need a graph paper composition notebook on the first day of class. This serves as your Lab Notebook. I look forward to learning and teaching with you in the fall! Find time to relax and recharge over the summer. I will be checking my district email, so feel free to contact me with any questions and concerns. My email address is [email protected]. 1 Physics Study Sheet for Math Algebra Skills 1. Solve an equation for any variable. Solve the following for x. ay a) v + w = x2yz c) bx 2 1 1 21y b) d) x 32 x 32 2. Be able to reduce fractions containing powers of ten. 2 3 10 4 10 a) 10 b) 103 106 3.
    [Show full text]
  • Quantum Theory, Quantum Mechanics) Part 1
    Quantum physics (quantum theory, quantum mechanics) Part 1 1 Outline Introduction Problems of classical physics Black-body Radiation experimental observations Wien’s displacement law Stefan – Boltzmann law Rayleigh - Jeans Wien’s radiation law Planck’s radiation law photoelectric effect observation studies Einstein’s explanation Quantum mechanics Features postulates Summary Quantum Physics 2 Question: What do these have in common? lasers solar cells transistors computer chips CCDs in digital cameras Ipods superconductors ......... Answer: They are all based on the quantum physics discovered in the 20th century. 3 “Classical” vs “modern” physics 4 Why Quantum Physics? “Classical Physics”: developed in 15th to 20th century; provides very successful description “macroscopic phenomena, i.e. behavior of “every day, ordinary objects” o motion of trains, cars, bullets,…. o orbit of moon, planets o how an engine works,.. o Electrical and magnetic phenomena subfields: mechanics, thermodynamics, electrodynamics, “There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.” 5 --- William Thomson (Lord Kelvin), 1900 Why Quantum Physics? – (2) Quantum Physics: developed early 20th century, in response to shortcomings of classical physics in describing certain phenomena (blackbody radiation, photoelectric effect, emission and absorption spectra…) describes microscopic phenomena, e.g. behavior of atoms, photon-atom scattering and flow of the electrons in a semiconductor.
    [Show full text]
  • General Technical Base Qualification Standard
    General Technical Base Qualification Standard DOE-STD-1146-2007 Reaffirmed March 2015 June 2016 Reference Guide The Functional Area Qualification Standard References Guides are developed to assist operators, maintenance personnel, and the technical staff in the acquisition of technical competence and qualification within the Technical Qualification Program (TQP). Please direct your questions or comments related to this document to Learning and Career Management, TQP Manager, NNSA Albuquerque Complex. This page is intentionally blank. TABLE OF CONTENTS FIGURES ...................................................................................................................................... iii TABLES ........................................................................................................................................ iii VIDEOS ........................................................................................................................................ iii ACRONYMS ................................................................................................................................. v PURPOSE ...................................................................................................................................... 1 SCOPE ........................................................................................................................................... 1 PREFACE .....................................................................................................................................
    [Show full text]
  • Fundamentals of Physics 10Th Edition
    PHY241 UNIVERSITY PHYSICS III Heat, entropy, and laws of thermodynamics; wave propagation; geometrical and physical optics; introduction to special relativity. These sites were selected to aid in the study of mechanics and thermodynamics at the college and university level. We tried to stay close to the Welcome page for each website so it would not be lost easily as the semester changes. text : Fundamentals of Physics 10th Edition Links Date Existing or Replacement Site Description Cool Links The National Institute of Standards & Technology A great resource for standards and recently published information. The National Institute of Standards & Technology May-11 http://www.nist.gov/index.html There are links to take you can where you want to go. Physics Resources A comprehensive resource for physics jokes, journals, employment, and recently published information. Physics Resources May-11 http://www.physlink.com/ There is also a question and answer site. There are links to take you the national labs. This site is heavy on graphics. Physics Resources from U. Penn. A comprehensive resource for physics from the University of Penn. This is a great site. Physics Resources from U. Penn May-11 https://www.physics.upenn.edu/resources/physics-astronomy-links There are links to take you the national labs. This site is heavy on graphics. Physics Linkage Page Univerversity of N. C. May-11 http://physics.unc.edu/research-pages/ Physics Link Page Physics Linkage Page Eastern Illinois University May-11 http://www.eiu.edu/~physics/important_links.php Physics Link Page Physics Site with Tutorials May-11 http://www.dl.ket.org/physics/ Physics Tutorials May-11 http://www.physicsclassroom.com/ Physics Tutorials Online Physics Courses May-11 http://academicearth.org/subjects/physics Sites with Multiple Course Material College level Physics A algebra/trig based set of lectures beginning with motion and ending with nuclear physics.
    [Show full text]
  • General Relativity and Modified Gravity
    General Relativity and Modified Gravity Dimitrios Germanis September 30, 2011 Abstract In this paper we present a detailed review of the most widely ac- cepted theory of gravity: general relativity. We review the Einstein- Hilbert action, the Einstein field equations, and we discuss the various astrophysical tests that have been performed in order to test Einstein’s theory of gravity. We continue by looking at alternative formulations, such as the Palatini formalism, the Metric-Affine gravity, the Vier- bein formalism, and others. We then present and analytically discuss a modification of General Relativity via the Chern-Simons gravity cor- rection term. We formulate Chern-Simons modified gravity, and we provide a derivation of the modified field equations by embedding the 3D-CS theory into the 4D-GR. We continue by looking at the appli- cations of the modified theory to CMB polarization, and review the various astrophysical tests that are used to test this theory. Finally, we look at f(R) theories of gravity and specifically, f(R) in the met- ric formalism, f(R) in the Palatini formalism, f(R) in the metric-affine formalism, and the various implications of these theories in cosmology, astrophysics, and particle physics. 1 Contents 1 Introduction 3 2 General Relativity 7 2.1 Foundations of GR . 7 2.2 Einstein’s Theory of GR . 16 2.3 The Einstein-Hilbert Action . 18 2.4 Einstein’s Field Equations . 20 2.5 Astrophysical Tests . 23 3 Alternative Formulations 28 3.1 The Palatini Formalism . 28 3.2 Metric-Affine Gravity . 31 3.3 The Vierbein Formalism .
    [Show full text]
  • PHYS 6601C: Learning and Teaching Algebra-Based Physics: Waves, Quantum & Nuclear Physics
    PHYS 6601C: Learning and Teaching Algebra-Based Physics: Waves, Quantum & Nuclear Physics Instructor: Yuriy Zavorotniy Email: [email protected] Course Credit: 2.0 NJCTL credits Dates & Times: This is a 2-credit, self-paced course, covering 6 modules of content. The exact number of hours that you can expect to spend on each module will vary based upon the module coursework, as well as your study style and preferences. You should plan to spend 6-12 hours per module, completing the module slides, readings, short answer assignments, labs, mastery exercises, practice problems, and module exams. COURSE DESCRIPTION: This is the last of three mini-courses which, together, are designed for those who are learning to teach Algebra-Based physics for middle school or high school students, focusing on conveying physics and mathematical concepts and understandings. Underlying themes are physics connections to everyday life, applications of mathematics in physics, problem solving, and hands on laboratory experience. The course presents physics as the foundation for studying chemistry, biology and advanced mathematics. Technology serves as a tool to establish these connections through exploration, problem solving, formative assessment, presentation, and communication. New Points: This final course is comprised of modern physics, including Simple Harmonic Motion, Waves, Light and the Bohr model of the Hydrogen atom for the last 20%. The order of the topics has been geared towards reinforcing skills in algebra and requires no trigonometry. This is accomplished by only including problems that can be simplified to one- dimensional form. While vectors are introduced, they are only added and subtracted in one dimension at a time.
    [Show full text]
  • A Modified Nuclear Model for Binding Energy of Nuclei And
    A MODIFIED NUCLEAR MODEL FOR BINDING ENERGY OF NUCLEI AND THE ISLAND OF STABILITY BY KENNETH KIPCHUMBA SIRMA A THESIS SUBMITTED IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE AWARD OF THE DEGREE OF DOCTOR OF PHILOSOPHY IN PHYSICS, UNIVERSITY OF ELDORET, KENYA. MAY, 2021 ii DECLARATION Declaration by the Candidate I declare that this is my original and personal work and has not been presented for a degree in any other university. This thesis is not to be reproduced without the prior written permission of the author and/or University of Eldoret. Kenneth Kipchumba Sirma ______________________________ _______________________ SC/PHD/002/15 Date Approval by Supervisors This thesis has been submitted for examination with our approval as University Supervisors. ______________________________ _______________________ Prof. Kapil M. Khanna Date Department of Physics University of Eldoret, Kenya. ______________________________ _______________________ Dr. Samuel L. Chelimo Date Physics Department University of Eldoret, Kenya. iii DEDICATION To my beloved mum Grace for her unconditional love, advice and support. To our children Gael and Abby you are blessings. My wife Jacinta, for her love and care. iv ABSTRACT A new nuclear model of quantifying binding energy of nuclei is proposed. The nucleus is assumed to be composed of two regions; the inner core region and surface region. The inner core is assumed to be composed of Z proton-neutron pairs (Z=N) and the surface region is composed of the unpaired neutrons for a nucleus in which N>Z. The interaction between the core and neutrons in the surface region is assumed to be such that it leads to an average potential Vo in which each neutron in the surface region can move.
    [Show full text]
  • Lecture 5: Kirchhoff's Laws in Circuits
    8/22/2019 Recommended learning opportunities • Workshops (as announced each week) • Office Hours Room 1005 (near lab), Monday-Friday • CARE Grainger Library • Honors projects targeting James Scholars, ECE110+ECE120 Encountering various difficulties? Contact your Instructor, lab TA, or the advising office on the second floor (2120 ECEB)! 1 Lecture 1: ECE110 Introduction to Electronics: Key Intro Concepts Charge Current Voltage 2 8/22/2019 The Field of Study Defined “Engineers use the knowledge of mathematics and natural sciences gained by study, experience, and practice, applied with judgment, to develop ways to economically utilize the materials and forces of nature for the benefit of mankind. “ - ABET (Accreditation Board for Engineering and Technology) Electrical engineering (EE) is a field of engineering that generally deals with the study and application of electricity, electronics, and electromagnetism - WikiPedia 3 A short history of Electrical Engineering 4 8/22/2019 Charge • Charge is measured in coulombs (퐶) • Capital or lowercase “Q” is the variable typically used to represent charge • an electron is a charged subatomic particle • the coulomb is extremely large compared to the charge of a single electron −19 −1.6 × 10 퐶 (푛표푡푎푡표푛 푐ℎ푎푛푔푒) −1.6 e − 19 퐶 푒푙푒푐푡푟표푛 = 푒푙푒푐푡푟표푛 • Electronics is much more than just movement of electrons 5 Current: the rate at which Charge moves • Current is measured in units of amps (퐴) • Capital or lowercase “I” is the variable typically used to represent current…it means intensity. • Electric current is the flow of electric charge in time (퐶/푠) 푑푞 푡 푡 = 푑푡 Image is public domain. • The ampere is the unit of electric current 1 퐴 = 1 퐶/푠 • Current is measured by an ammeter 6 8/22/2019 “DC” Current For constant rates called “Direct Current” or “DC”, we typically use capitalized variables and can replace the differential with observations in some time, Δ푡.
    [Show full text]
  • Quantum Entanglement: an Exploration of a Weird Phenomenon1
    Sabiduria, Vol. 1, 2 Quantum Entanglement: A Weird Phenomenon 1 Quantum Entanglement: An Exploration of a Weird Phenomenon1 Jean S. Joseph Abstract: In this paper, quantum entanglement, which is a quantum mechanical phenomenon where particles can have influence on others regardless of the distance between them, is deeply explored. A historical context is first presented to trace the different events that led to quantum mechanics as a theory; its mathematical formalism is then presented to help understanding the theoretical aspect of quantum entanglement. Later, the validity of quantum entanglement is explored where arguments from Einstein, Bell, and Neumann are presented and where experiments from Clauser, Holt, Shimony, and Horne; and Aspect, Grangier, and Roger are presented. 1 I would like to thank Professor Carlos Ramos for willing to work with me on this paper, Robert Slattery for proofreading it, and the reviewers for their useful suggestions. Sabiduria, Vol. 1, 2 Quantum Entanglement: A Weird Phenomenon 2 “God does not play dice,” confidently affirmed Albert Einstein in his fight against quantum mechanics. Indeed, Einstein did not appreciate the stochastic nature of quantum mechanics that represented a threat to determinism, which had been the ultimate criterion for science. However, over the years, quantum mechanics has shown that it is the best candidate to describe the subatomic world even though its phenomena contradict humans’ most intuitive understanding of their physical world. One of those phenomena is quantum entanglement, where two particles, after some interaction, have some influence on each other regardless of the distance between them, distance that can theoretically be light-years between them.
    [Show full text]
  • Special Theory of Relativity
    Special Theory of Relativity Marc McGuigan North Quincy High School Outline Introduction Relativity The speed of light Einstein’s Solution Time Space Conclusion Introduction The Special Theory of Relativity is the theory put forth by Albert Einstein in his 1905 paper, “On the Electrodynamics of Moving Bodies” “Special” because it applies the theory of relativity to inertial reference frames in flat space-time (no gravity) Relative Motion •Who is moving? •How do we know? •Up until Einstein we used addition and subtraction to calculate the observed speed to other objects Relative Motion Motion is relative as long as you are not accelerating! There is no experiment that you can do in an inertial reference frame that will distinguish it from another inertial reference frame vobject−ground =vobject−train + train v −ground The Speed of Light 670 million miles per hour (in a vacuum) 186,000 miles per second Light always moves at the same speed You can never catch a beam of light! Postulates of Special Relativity 1. “The laws of electrodynamics and optics will be valid for all frames of reference in which the laws of mechanics hold good (non-accelerating frames).” 2. “Light is always propagated in empty space with a definite velocity c that is independent of the state of motion of the emitting body; here the velocity of light c is defined as the two-way velocity, determined with a single clock.” Simultaneous Events Events that are simultaneous for observers in one reference frame are not necessarily simultaneous to observers in
    [Show full text]
  • Radiation & Autoionization Processes
    Radiation & Autoionization Processes Atomic Theory and Computations | Lecture script | IAEA-ICTP School, Trieste, February 2017 Stephan Fritzsche Helmholtz-Institut Jena & Theoretisch-Physikalisches Institut, Friedrich-Schiller-Universit¨atJena, Fr¨obelstieg 3, D-07743 Jena, Germany Monday 27th February, 2017 1. Atomic theory and computations in a nut-shell 1.1. Atomic spectroscopy: Structure & collisions Atomic processes & interactions: ã Spontaneous emission/fluorescence: ... occurs without an ambient electromagnetic field; related also to absorption. ã Stimulated emission: ... leads to photons with basically the same phase, frequency, polarization, and direction of propagation as the incident photons. ã Photoionization: ... release of free electrons. ã Rayleigh and Compton scattering: ... Elastic and inelastic scattering of X-rays and gamma rays by atoms and molecules. ã Thomson scattering: ... elastic scattering of electromagnetic radiation by a free charged particle (electrons, muons, ions); low-energy limit of Compton scattering. ã Multi-photon excitation, ionization and decay: ... non-linear electron-photon interaction. ã Autoionization: ... nonradiative electron emission from (inner-shell) excited atoms. ã Electron-impact excitation & ionization: ... excited and ionized atoms; occurs frequently in astro-physical and laboratory plasmas. 3 1. Atomic theory and computations in a nut-shell ã Elastic & inelastic electron scattering: ... reveals electronic structure of atoms and ions; important for plasma physics. ã Pair production: ... creation of particles and antiparticles from the internal of light with matter (electron-positron pairs). ã Delbr¨uck scattering: ... deflection of high-energy photons in the Coulomb field of atomic nuclei; a consequence of vacuum polarization. ã ... ã In practice, the distinction and discussion of different atomic and electron-photon interaction processes also depends on the particular community/spectroscopy.
    [Show full text]
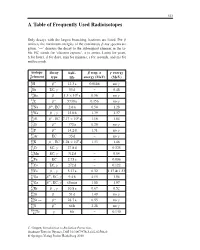
  • A Table of Frequently Used Radioisotopes
    323 A Table of Frequently Used Radioisotopes Only decays with the largest branching fractions are listed. For β emitters the maximum energies of the continuous β-ray spectra are given. ‘→’ denotes the decay to the subsequent element in the ta- ble. EC stands for ‘electron capture’, a (= annus, Latin) for years, h for hours, d for days, min for minutes, s for seconds, and ms for milliseconds. isotope decay half- β resp. α γ energy A Z element type life energy (MeV) (MeV) 3 β− . γ 1H 12 3a 0.0186 no 7 γ 4Be EC, 53 d – 0.48 10 β− . × 6 γ 4Be 1 5 10 a 0.56 no 14 β− γ 6C 5730 a 0.156 no 22 β+ . 11Na ,EC 2 6a 0.54 1.28 24 β− γ . 11Na , 15 0h 1.39 1.37 26 β+ . × 5 13Al ,EC 7 17 10 a 1.16 1.84 32 β− γ 14Si 172 a 0.20 no 32 β− . γ 15P 14 2d 1.71 no 37 γ 18Ar EC 35 d – no 40 β− . × 9 19K ,EC 1 28 10 a 1.33 1.46 51 γ . 24Cr EC, 27 8d – 0.325 54 γ 25Mn EC, 312 d – 0.84 55 . 26Fe EC 2 73 a – 0.006 57 γ 27Co EC, 272 d – 0.122 60 β− γ . 27Co , 5 27 a 0.32 1.17 & 1.33 66 β+ γ . 31Ga , EC, 9 4h 4.15 1.04 68 β− γ 31Ga , EC, 68 min 1.88 1.07 85 β− γ .
    [Show full text]