On Complexes Equivalent to S3-Bundles Over S4
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Disability Classification System
CLASSIFICATION SYSTEM FOR STUDENTS WITH A DISABILITY Track & Field (NB: also used for Cross Country where applicable) Current Previous Definition Classification Classification Deaf (Track & Field Events) T/F 01 HI 55db loss on the average at 500, 1000 and 2000Hz in the better Equivalent to Au2 ear Visually Impaired T/F 11 B1 From no light perception at all in either eye, up to and including the ability to perceive light; inability to recognise objects or contours in any direction and at any distance. T/F 12 B2 Ability to recognise objects up to a distance of 2 metres ie below 2/60 and/or visual field of less than five (5) degrees. T/F13 B3 Can recognise contours between 2 and 6 metres away ie 2/60- 6/60 and visual field of more than five (5) degrees and less than twenty (20) degrees. Intellectually Disabled T/F 20 ID Intellectually disabled. The athlete’s intellectual functioning is 75 or below. Limitations in two or more of the following adaptive skill areas; communication, self-care; home living, social skills, community use, self direction, health and safety, functional academics, leisure and work. They must have acquired their condition before age 18. Cerebral Palsy C2 Upper Severe to moderate quadriplegia. Upper extremity events are Wheelchair performed by pushing the wheelchair with one or two arms and the wheelchair propulsion is restricted due to poor control. Upper extremity athletes have limited control of movements, but are able to produce some semblance of throwing motion. T/F 33 C3 Wheelchair Moderate quadriplegia. Fair functional strength and moderate problems in upper extremities and torso. -

Carbonaceous Aerosol Microphysics
Atmos. Chem. Phys. Discuss., 10, 4543–4592, 2010 Atmospheric www.atmos-chem-phys-discuss.net/10/4543/2010/ Chemistry ACPD © Author(s) 2010. This work is distributed under and Physics 10, 4543–4592, 2010 the Creative Commons Attribution 3.0 License. Discussions This discussion paper is/has been under review for the journal Atmospheric Chemistry Carbonaceous and Physics (ACP). Please refer to the corresponding final paper in ACP if available. aerosol microphysics S. E. Bauer et al. A global modeling study on Title Page carbonaceous aerosol microphysical Abstract Introduction Conclusions References characteristics and radiative forcing Tables Figures S. E. Bauer1,2, S. Menon3, D. Koch1,2, T. C. Bond4, and K. Tsigaridis1 J I 1NASA Goddard Institute for Space Studies, New York, NY, USA J I 2The Earth Institute, Columbia University, New York, NY, USA 3Lawrence Berkeley National Laboratory, Berkeley, CA, USA Back Close 4University of Illinois, Urbana-Champaign, IL, USA Full Screen / Esc Received: 20 January 2010 – Accepted: 8 February 2010 – Published: 15 February 2010 Correspondence to: S. E. Bauer ([email protected]) Printer-friendly Version Published by Copernicus Publications on behalf of the European Geosciences Union. Interactive Discussion 4543 Abstract ACPD Recently, attention has been drawn towards black carbon aerosols as a short-term cli- mate warming mitigation candidate. However the global and regional impacts of the 10, 4543–4592, 2010 direct, cloud-indirect and semi-direct forcing effects are highly uncertain, due to the 5 complex nature of aerosol evolution and the way that mixed, aged aerosols interact Carbonaceous with clouds and radiation. A detailed aerosol microphysical scheme, MATRIX, em- aerosol microphysics bedded within the GISS climate model is used in this study to present a quantitative assessment of the impact of microphysical processes involving black carbon, such as S. -
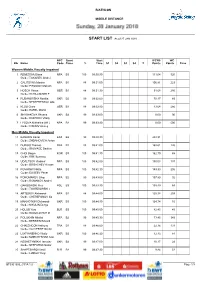
List Biathlon Middle Distance
BIATHLON MIDDLE DISTANCE START LIST As of 27 JAN 2018 NPC Sport Start IPCNS WC Bib Name Code Class % Time S1 S2 S3 S4 T Points Points Time Women Middle,Visually Impaired 1 REMIZOVA Elena NPA B3 100 09:30:30 111.04 320 Guide: TOKAREV Andrei 2 GALITSYNA Marina NPA B1 88 09:31:00 106.81 223 Guide: PIROGOV Maksim 3 HOSCH Vivian GER B1 88 09:31:30 91.68 280 Guide: SCHILLINGER F 4 RUBANOVSKA Natalia UKR B2 99 09:32:00 70.17 85 Guide: NESTERENKO Lada 5 KLUG Clara GER B1 88 09:32:30 13.64 280 Guide: HARTL Martin 6 SHYSHKOVA Oksana UKR B2 99 09:33:00 0.00 90 Guide: KAZAKOV Vitaliy 7 LYSOVA Mikhalina (WL) NPA B2 99 09:33:30 0.00 500 Guide: IVANOV Alexey Men Middle,Visually Impaired 11 KANAFIN Kairat KAZ B2 99 09:40:30 204.91 Guide: ZHDANOVICH Anton 12 DUBOIS Thomas FRA B1 88 09:41:00 168.61 126 Guide: SAUVAGE Bastien 13 CHOI Bogue KOR B3 100 09:41:30 162.70 65 Guide: KIM Hyunwoo 14 UDALTSOV Vladimir NPA B3 100 09:42:00 150.03 137 Guide: BOGACHEV Ruslan 15 POVAROV Nikita NPA B3 100 09:42:30 149.93 206 Guide: ELISEEV Pavel 16 PONOMAREV Oleg NPA B2 99 09:43:00 137.80 32 Guide: ROMANOV Andrei 17 GARBOWSKI Piotr POL B3 100 09:43:30 135.49 69 Guide: TWARDOWSKI J 18 ARTEMOV Aleksandr NPA B1 88 09:44:00 125.38 209 Guide: CHEREPANOV Ilia 19 MAKHOTKIN Oleksandr UKR B3 100 09:44:30 124.74 16 Guide: NIKULIN Denys 20 HOLUB Yury BLR B3 100 09:45:00 82.45 45 Guide: BUDZILOVICH D 21 POLUKHIN Nikolai NPA B2 99 09:45:30 73.45 345 Guide: BEREZIN Eduard 22 CHALENCON Anthony FRA B1 88 09:46:00 22.36 133 Guide: VALVERDE Simon 23 LUK'YANENKO Vitaliy UKR B3 100 09:46:30 -

(VA) Veteran Monthly Assistance Allowance for Disabled Veterans
Revised May 23, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L. -

Official Rules
2018 Willamette Valley Youth Football & Cheer OFFICIAL RULES Page 1 Willamette Valley Youth Football & Cheer Table of Contents Part I – The WVYFC Program ............................................................... 5 Article 1: Members Code of Conduct ............................................. 5 Part II – WVYFC Structure .................................................................... 7 Part III – Regulations ............................................................................ 7 Article 1: Authority of League ......................................................... 7 Article 2: Boundaries ....................................................................... 7 Article 3: Coaches Requirements .................................................... 8 Article 4: Registration ..................................................................... 8 Article 5: Formation of Teams ........................................................ 9 Article 6: Mandatory Cuts ............................................................. 10 Article 7: Voluntary Cuts ............................................................... 10 Article 8: Certification ................................................................... 10 Article 9: Retention of Eligibility ................................................... 10 Article 10: No All Stars .................................................................. 10 Article 11: Awards ......................................................................... 11 Article 12: Practice (Definition & Date -

The Paralympic Athlete Dedicated to the Memory of Trevor Williams Who Inspired the Editors in 1997 to Write This Book
This page intentionally left blank Handbook of Sports Medicine and Science The Paralympic Athlete Dedicated to the memory of Trevor Williams who inspired the editors in 1997 to write this book. Handbook of Sports Medicine and Science The Paralympic Athlete AN IOC MEDICAL COMMISSION PUBLICATION EDITED BY Yves C. Vanlandewijck PhD, PT Full professor at the Katholieke Universiteit Leuven Faculty of Kinesiology and Rehabilitation Sciences Department of Rehabilitation Sciences Leuven, Belgium Walter R. Thompson PhD Regents Professor Kinesiology and Health (College of Education) Nutrition (College of Health and Human Sciences) Georgia State University Atlanta, GA USA This edition fi rst published 2011 © 2011 International Olympic Committee Blackwell Publishing was acquired by John Wiley & Sons in February 2007. Blackwell’s publishing program has been merged with Wiley’s global Scientifi c, Technical and Medical business to form Wiley-Blackwell. Registered offi ce: John Wiley & Sons, Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK Editorial offi ces: 9600 Garsington Road, Oxford, OX4 2DQ, UK The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK 111 River Street, Hoboken, NJ 07030-5774, USA For details of our global editorial offi ces, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com/wiley-blackwell The right of the author to be identifi ed as the author of this work has been asserted in accordance with the UK Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher. -

Tps2583x-Q1 USB Type-C and BC1.2 5-V 3.5-A Output, 36-V Input Synchronous Step-Down DC/DC Regulator with Cable Compensation
TPS25830-Q1, TPS25831-Q1 www.ti.com SLVSDP6F – JUNETPS25830-Q1, 2018 – REVISED TPS25831-Q1 AUGUST 2020 SLVSDP6F – JUNE 2018 – REVISED AUGUST 2020 TPS2583x-Q1 USB Type-C and BC1.2 5-V 3.5-A Output, 36-V Input Synchronous Step-Down DC/DC Regulator with Cable Compensation 1 Features –VBUS Short-to-VBAT protection – DP_IN and DM_IN Short-to-VBAT and VBUS • AEC-Q100 Qualified for automotive applications: – CC1 and CC2 Short-to-VBAT protection – Temperature grade 1: –40°C to +125°C, TA – DP_IN, DM_IN, CCx IEC 61000-4-2 rated – HBM ESD classification level H2 • ±8kV Contact and ±15kV air discharge – CDM ESD classification level C5 • Fault flag reports • Functional Safety-Capable • 32-Pin QFN package with Wettable Flank – Documentation available to aid functional safety system design 2 Applications • Synchronous buck DC/DC regulator • Automotive Infotainment – Input voltage range: 4.5 V to 36 V • USB Media Hubs – Output current: 3.5 A • USB Charger Ports – 5.1-V Output voltage with ±1% accuracy 3 Description – Current mode control – Adjustable frequency: 300 kHz to 2.2 MHz The TPS2583x-Q1 is a USB Type-C and BC1.2 charging port controller that includes a synchronous – Frequency synchronization to external clock DC/DC converter. With cable droop compensation, – FPWM with spread-spectrum dithering the VBUS voltage remains constant regardless of load – Internal compensation for ease of use current, ensuring connected portable devices are • Compliant to USB-IF standards charged at optimal current and voltage. – USB Type-C Rev 1.3 The TPS2583x-Q1 also integrates short to battery • CC logic, VCONN source and discharge protection on VBUS, CC1, CC2, DM_IN and DP_IN • USB cable polarity detection ( POL) pins. -

Lecture 3: MIPS Instruction Set
Lecture 3: MIPS Instruction Set • Today’s topic: More MIPS instructions Procedure call/return • Reminder: Assignment 1 is on the class web-page (due 9/7) 1 Memory Operands • Values must be fetched from memory before (add and sub) instructions can operate on them Load word Register Memory lw $t0, memory-address Store word Register Memory sw $t0, memory-address How is memory-address determined? 2 Memory Address • The compiler organizes data in memory… it knows the location of every variable (saved in a table)… it can fill in the appropriate mem-address for load-store instructions int a, b, c, d[10] … Memory Base address 3 Immediate Operands • An instruction may require a constant as input • An immediate instruction uses a constant number as one of the inputs (instead of a register operand) addi $s0, $zero, 1000 # the program has base address # 1000 and this is saved in $s0 # $zero is a register that always # equals zero addi $s1, $s0, 0 # this is the address of variable a addi $s2, $s0, 4 # this is the address of variable b addi $s3, $s0, 8 # this is the address of variable c addi $s4, $s0, 12 # this is the address of variable d[0] 4 Memory Instruction Format • The format of a load instruction: destination register source address lw $t0, 8($t3) any register a constant that is added to the register in brackets 5 Example Convert to assembly: C code: d[3] = d[2] + a; Assembly: # addi instructions as before lw $t0, 8($s4) # d[2] is brought into $t0 lw $t1, 0($s1) # a is brought into $t1 add $t0, $t0, $t1 # the sum is in $t0 sw $t0, 12($s4) -

Athletes with Disability Handbook 2009
1 Athletes with Disability Handbook 2009 Athletes with Disability Handbook ATHLETES WITH DISABILITY COMMITTEE Canadian Academy of Sport Medicine 5330 rue Canotek Road, Unit (é) 4 Ottawa, (ON) K1J 9C1 Tel. (613) 748-5851 Fax (613 748-5792 1-877-585-2394 Internet: [email protected] www.casm-acms.org 2 Athletes with Disability Handbook 2009 Acknowledgements: A special thanks to Dr. Dhiren Naidu, Dr. Nancy Dudek, and Dr. Doug Dittmer for helping with the organization and content of this manual. I would also like to thank the many authors who contributed their time and expertise to write the chapters in this manual. Without your help this project would not have been a success. Sincerely, Russ O’Connor MD, FRCPC, CASM Dip Sport Med 3 Athletes with Disability Handbook 2009 Table of Contents 1. RED FLAGS .................................................................................................................. 5 TOPIC: CHANGE IN MOTOR OR SENSORY FUNCTION ......................................................... 6 TOPIC: NEW OR SIGNIFICANT CHANGE IN SPASTICITY ...................................................... 7 TOPIC: AUTONOMIC DYSREFLEXIA (AD) .................................................................................. 8 TOPIC: FRACTURES IN A PARALYZED ATHLETE ................................................................... 9 TOPIC: SWOLLEN LIMB IN AN ATHLETE WITH A NEUROLOGICAL IMPAIRMENT ....... 10 TOPIC: BALCOFEN WITHDRAWAL SYNDROME (BWS) ....................................................... 11 TOPIC: FEVER ................................................................................................................................ -

UMTS); LTE; E-UTRA, UTRA and GSM/EDGE; Multi-Standard Radio (MSR) Base Station (BS) Radio Transmission and Reception (3GPP TS 37.104 Version 9.5.0 Release 9)
ETSI TS 137 104 V9.5.0 (2011-06) Technical Specification Digital cellular telecommunications system (Phase 2+); Universal Mobile Telecommunications System (UMTS); LTE; E-UTRA, UTRA and GSM/EDGE; Multi-Standard Radio (MSR) Base Station (BS) radio transmission and reception (3GPP TS 37.104 version 9.5.0 Release 9) 3GPP TS 37.104 version 9.5.0 Release 9 1 ETSI TS 137 104 V9.5.0 (2011-06) Reference RTS/TSGR-0437104v950 Keywords GSM, LTE, UMTS ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice Individual copies of the present document can be downloaded from: http://www.etsi.org The present document may be made available in more than one electronic version or in print. In any case of existing or perceived difference in contents between such versions, the reference version is the Portable Document Format (PDF). In case of dispute, the reference shall be the printing on ETSI printers of the PDF version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at http://portal.etsi.org/tb/status/status.asp If you find errors in the present document, please send your comment to one of the following services: http://portal.etsi.org/chaircor/ETSI_support.asp Copyright Notification No part may be reproduced except as authorized by written permission. -

2019 Prohibited List
THE WORLD ANTI-DOPING CODE INTERNATIONAL STANDARD PROHIBITED LIST JANUARY 2019 The official text of the Prohibited List shall be maintained by WADA and shall be published in English and French. In the event of any conflict between the English and French versions, the English version shall prevail. This List shall come into effect on 1 January 2019 SUBSTANCES & METHODS PROHIBITED AT ALL TIMES (IN- AND OUT-OF-COMPETITION) IN ACCORDANCE WITH ARTICLE 4.2.2 OF THE WORLD ANTI-DOPING CODE, ALL PROHIBITED SUBSTANCES SHALL BE CONSIDERED AS “SPECIFIED SUBSTANCES” EXCEPT SUBSTANCES IN CLASSES S1, S2, S4.4, S4.5, S6.A, AND PROHIBITED METHODS M1, M2 AND M3. PROHIBITED SUBSTANCES NON-APPROVED SUBSTANCES Mestanolone; S0 Mesterolone; Any pharmacological substance which is not Metandienone (17β-hydroxy-17α-methylandrosta-1,4-dien- addressed by any of the subsequent sections of the 3-one); List and with no current approval by any governmental Metenolone; regulatory health authority for human therapeutic use Methandriol; (e.g. drugs under pre-clinical or clinical development Methasterone (17β-hydroxy-2α,17α-dimethyl-5α- or discontinued, designer drugs, substances approved androstan-3-one); only for veterinary use) is prohibited at all times. Methyldienolone (17β-hydroxy-17α-methylestra-4,9-dien- 3-one); ANABOLIC AGENTS Methyl-1-testosterone (17β-hydroxy-17α-methyl-5α- S1 androst-1-en-3-one); Anabolic agents are prohibited. Methylnortestosterone (17β-hydroxy-17α-methylestr-4-en- 3-one); 1. ANABOLIC ANDROGENIC STEROIDS (AAS) Methyltestosterone; a. Exogenous* -

Layman's Guide to Classification
LAYMAN’S GUIDE TO CLASSIFICATION Swimming is the only sport that combines the conditions of limb loss, cerebral palsy (coordination and movement restrictions), spinal cord injury (weakness or paralysis involving any combination of the limbs) and other disabilities, such as Dwarfism; major joint restriction condition across classes. • Classes S1-S10 – are allocated to swimmers with a physical impairment • Classes S11-S13 – are allocated to swimmers with a visual impairment • Class S14 – is allocated to swimmers with an intellectual impairment • Class S15 – is allocated to swimmers with a hearing impairment • The Prefix S to the Class denotes the class for Freestyle, Backstroke and Butterfly • The Prefix SB to the class denotes the class for Breaststroke • The Prefix SM to the class denotes the class for Individual Medley The range is from the swimmers with a more severe impairment (S1, SB1, SM1) to those with the impairment (S10, SB9, SM10) In any one class some swimmers may start with a dive or in the water depending on their impairment. This is factored in when classifying an athlete. The following examples are only a guide - some conditions not mentioned here may also fit the following classes THE FUNCTIONAL CLASSIFICATION SYSTEM (FCS) PHYSICAL IMPAIRMENTS S1, SB1, SM1 Swimmers in this class would usually be wheelchair users and may have a higher dependency for their every day needs. Examples: Swimmers with very severe coordination problems in all four limbs or have no use of their legs, trunk, hands and minimal use of their shoulders only. Swimmers in this class usually only swim on their back.