A System of Location Models for the Evaluation of Long Term Impacts of Transport Policies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
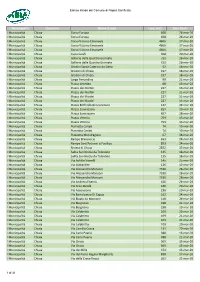
Municipalità Quartiere Nome Strada Lung.(Mt) Data Sanif
Elenco strade del Comune di Napoli Sanificate Municipalità Quartiere Nome Strada Lung.(mt) Data Sanif. I Municipalità Chiaia Corso Europa 608 24-mar-20 I Municipalità Chiaia Corso Europa 608 24-mar-20 I Municipalità Chiaia Corso Vittorio Emanuele 4606 17-mar-20 I Municipalità Chiaia Corso Vittorio Emanuele 4606 17-mar-20 I Municipalità Chiaia Corso Vittorio Emanuele 4606 17-mar-20 I Municipalità Chiaia Cupa Caiafa 368 20-mar-20 I Municipalità Chiaia Galleria delle Quattro Giornate 721 28-mar-20 I Municipalità Chiaia Galleria delle Quattro Giornate 721 28-mar-20 I Municipalità Chiaia Gradini Santa Caterina da Siena 52 18-mar-20 I Municipalità Chiaia Gradoni di Chiaia 197 18-mar-20 I Municipalità Chiaia Gradoni di Chiaia 197 18-mar-20 I Municipalità Chiaia Largo Ferrandina 99 21-mar-20 I Municipalità Chiaia Piazza Amedeo 68 13-mar-20 I Municipalità Chiaia Piazza dei Martiri 227 13-mar-20 I Municipalità Chiaia Piazza dei Martiri 227 21-mar-20 I Municipalità Chiaia Piazza dei Martiri 227 21-mar-20 I Municipalità Chiaia Piazza dei Martiri 227 13-mar-20 I Municipalità Chiaia Piazza Roffredo Beneventano 147 24-mar-20 I Municipalità Chiaia Piazza Sannazzaro 657 20-mar-20 I Municipalità Chiaia Piazza Sannazzaro 657 28-mar-20 I Municipalità Chiaia Piazza Vittoria 759 13-mar-20 I Municipalità Chiaia Piazza Vittoria 759 13-mar-20 I Municipalità Chiaia Piazzetta Cariati 74 19-mar-20 I Municipalità Chiaia Piazzetta Cariati 74 19-mar-20 I Municipalità Chiaia Piazzetta Mondragone 67 18-mar-20 I Municipalità Chiaia Rampe Brancaccio 653 24-mar-20 I Municipalità -

The Impact of Transport Management on the Local Activities System: the Role of Limited Traffic Zones
Urban Transport XX 669 The impact of transport management on the local activities system: the role of limited traffic zones L. Biggiero Department of Civil, Building and Environmental Engineering, University Federico II of Naples, Italy Abstract The impacts of transportation in planning land use and activities are not always intended and can have unforeseen or unintended consequences such as congestion or evident impacts on the local economy where the interventions are conceived. This is the case for Limited Traffic Zones (LTZs), i.e. areas where cars are not allowed in them. In this paper, the impact of these measures on the local economy is analysed, considering as a case study the town of Napoli in the south of Italy, where two Limited Traffic Zones, in two different boroughs and years, named Vomero and Chiaia, have been introduced. Moreover, the impacts due to changes involving one of the LTZ’s areas are also observed and analysed through a before-after survey. The direct impact on traffic congestion has not been taken into account. More than 30% of all activities have been interviewed in the two restricted areas and some key points have been assessed for the successful or unsuccessful of car restriction measure. Retailers were also asked about their decrease in turnover in order to evaluate the effects of the LTZ’s area after taking into account the actual economic crisis. The survey showed how much the retailers require: efficient public transport; parking places as close as possible; residential and activity density and typology. Those are the main reasons for the success of the Vomero LTZ zone and of the failure of the Chaia restricted zone. -

Elenco Strade Sanificate Aggiornate Al 31 Marzo
ELENCO STRADE SANIFICATE AGGIORNATE AL 31 MARZO Municipalità Quartiere Nome Strada Lunghezza Data Bonifica I Municipalità Chiaia Corso Europa 608 24/03/2020 I Municipalità Chiaia Corso Vittorio Emanuele 4606 17/03/2020 I Municipalità Chiaia Cupa Caiafa 368 20/03/2020 I Municipalità Chiaia Galleria delle Quattro Giornate 721 28/03/2020 I Municipalità Chiaia Gradini del Petraio 232 27/03/2020 I Municipalità Chiaia Gradini Santa Caterina da Siena 52 18/03/2020 I Municipalità Chiaia Gradoni di Chiaia 197 18/03/2020 I Municipalità Chiaia Largo Ferrandina 99 21/03/2020 I Municipalità Chiaia Piazza Amedeo 68 13/03/2020 I Municipalità Chiaia Piazza dei Martiri 227 13/03/2020 I Municipalità Chiaia Piazza dei Martiri 227 21/03/2020 I Municipalità Chiaia Piazza Roffredo Beneventano 147 24/03/2020 I Municipalità Chiaia Piazza Sannazzaro 657 20/03/2020 I Municipalità Chiaia Piazza Sannazzaro 657 28/03/2020 I Municipalità Chiaia Piazza Vittoria 759 13/03/2020 I Municipalità Chiaia Piazzetta Cariati 74 19/03/2020 I Municipalità Chiaia Piazzetta Mondragone 67 18/03/2020 I Municipalità Chiaia Rampe Brancaccio 653 24/03/2020 I Municipalità Chiaia Rampe Sant'Antonio a Posillipo 893 24/03/2020 I Municipalità Chiaia Riviera di Chiaia 2872 13/03/2020 I Municipalità Chiaia Salita San Nicola da Tolentino 135 18/03/2020 I Municipalità Chiaia Via Achille Vianelli 145 25/03/2020 I Municipalità Chiaia Via Alabardieri 126 13/03/2020 I Municipalità Chiaia Via Alessandro Manzoni 7330 28/03/2020 I Municipalità Chiaia Via Andrea d'Isernia 426 24/03/2020 I Municipalità -

Carabinieri 112 Polizia 113 Vigili Del Fuoco 115 Pronto
CARABINIERI 112 POLIZIA 113 VIGILI DEL FUOCO 115 PRONTO SOCCORSO 118 SOCCORSO STRADALE 803.116 GUARDIA DI FINANZA 117 VIGILI URBANI 081-7513177 AUTO RUBATE 081-7941435 POLIZIA STRADALE 081-5954111 081-2208311 ANTIRACKET CARABINIERI 081-5484519 081-5484515 ANTIRACKET POLIZIA 081-7941544 GUARDIA COSTIERA 1530 CENTRO ANTIVELENI 081-545333 081-5451889 C.R.I. 800358358 C. di S. Leonardo 081-5469127 081-7702428 ASL 1. 081-7528.282 081-7520.696 081-7520850 Neapolis Ambulance Service 081-7406475 Service Assistance 081-5854620 Ambrosiana 081-5453565 081-5454656 Croce Bianca 081-5454656 Croce S. Raffaele 081-5872490 C. Azzurra 081-5453565 081-5463884 C. Verde di Napoli 081-5442078 081-5447603 F.lli Bourelly Serv. Ambulanza 081-5591600 Eliambulanze (gratuita diurna) 800.081118 Elicottero Aereo 081-5844319 081-5844355 Servizio Eli notturno 081-7122962 Guardia medica. Il servizio funziona:feriali ore 20-8; sabato e prefestivi dalle 10 fino alle 8 della giornata di nuovo feriale. S. Ferdinando Chiaia Posillipo 081-7613466 081-2547215 Fuorigrotta Bagnoli 081-2390161 081-7686425 Soccavo Pianura 081-7672183 081-2548370 Vomero Arenella 081-5780760 081-2549764 Chiaiano Piscinola Marianella Scampia 081-7021116 081-2546501 Stella S. Carlo Arena 081-7517510 081-2549240 Miano Secondigliano S. Pietro a Patierno 081-7372803 081-2546627 Montecalvario Avvocata S. Giuseppe Porto Mercato Pendino 081-2542424 081-5494338 S. Giovanni Barra Ponticelli 081-5969818 S. Lorenzo Vicaria Poggioreale 081-202343 081-2549185 Pediatria Il servizio funziona dalle 8,30 alle 14,30. S. Ferdinando Chiaia 081-2547076 Fuorigrotta 081-7646879 Soccavo Pianura 081-2548348 Chiaiano 081.5854235 Piscinola Marianella Scampia 081-5851899 081-7065056 Miano 081-2352532 Secondigliano S. -

Energy and Entropy Measures of Fuzzy Relations for Data Analysis
entropy Article Energy and Entropy Measures of Fuzzy Relations for Data Analysis Ferdinando Di Martino 1,2,* ID and Salvatore Sessa 1,2 ID 1 Dipartimento di Architettura, Università degli Studi di Napoli Federico II, Via Toledo 402, 80134 Napoli, Italy; [email protected] 2 Centro Interdipartimentale di Ricerca A. Calza Bini, Università degli Studi di Napoli Federico II, Via Toledo 402, 80134 Napoli, Italy * Correspondence: [email protected]; Tel.: +39-081-253-8904 Received: 18 April 2018; Accepted: 30 May 2018; Published: 31 May 2018 Abstract: We present a new method for assessing the strength of fuzzy rules with respect to a dataset, based on the measures of the greatest energy and smallest entropy of a fuzzy relation. Considering a fuzzy automaton (relation), in which A is the input fuzzy set and B the output fuzzy set, the fuzzy relation R1 with greatest energy provides information about the greatest strength of the input-output, and the fuzzy relation R2 with the smallest entropy provides information about uncertainty of the input-output relationship. We consider a new index of the fuzziness of the input-output based on R1 and R2. In our method, this index is calculated for each pair of input and output fuzzy sets in a fuzzy rule. A threshold value is set in order to choose the most relevant fuzzy rules with respect to the data. Keywords: fuzzy energy; fuzzy entropy; fuzzy rules; fuzzy relations 1. Introduction Let X = {x1, ... , xm} be a finite set and A be a fuzzy set of X. In [1,2] two categories of fuzziness, measures are defined as energy and entropy (see, e.g., also [3]). -

Gesac Tariffe Montaggio Lingue
Cyan - Magenta - ORO - Nero FRANÇAIS MAIRIE DE NAPLES – VII DIREZIONE CENTRALE TARIFS PREDEFINIS Euro Le client peut choisir parmi les tarifs prédéfinis suivants et doit les demander avant le début de la course POUR INFORMATIONS OU RECLAMATIONS: Servizio programmazione, Promozione e Controllo URBAINS Servizi di Trasporto Pubblico Hôtels du bord de mer -- Aéroport de Capodichino ou vice versa 19,00 Galleria Principe di Napoli - Piazza Museo Nazionale Aliscafi Mergellina -- Aéroport de Capodichino ou vice versa 19,00 80135 NAPOLI Gare Centrale (Hôtels limitrophes) -- Aéroport de Capodichino ou vice versa 12,50 Tel. 081 5441401 - fax 081 5642209 COMUNE DI NAPOLI email : [email protected] Musée de Capodimonte -- Musée de S. Martino ou vice versa 9,50 Place Municipio (Hôtels limitrophes) -- Musée de Capodimonte ou vice-versa 9,50 TARIFS ZONE URBAINE Aéroport de Capodichino -- Hôtels du Vomero -Fuorigrotta ou vice versa 19,00 Place Municipio (Hôtels limitrophes) -- Aéroport de Capodichino ou vice versa 16,00 PRISE EN CHARGE Gare Centrale -- Aliscafi Mergellina ou vice versa 12,50 Du lundi au samedi de 7:00 à 22:00 3,00 Gare Centrale -- Hôtels Fuorigrotta ou vice versa 16,00 Dimanche et jours fériés de 7:00 à 22:00 5,50 Gare de Mergellina -- Hôtels de Fuorigrotta ou vice versa 9,50 Tarif de nuit semaine dimanche jours fériés 22:00 à 7:00 5,50 Gare de Mergellina -- Hôtels d’Agnano ou vice versa 12,50 Tarif minimum de la course lundi au samedi de 7:00 à 22:00 4,50 Quai Beverello -- Gare centrale ou vice versa 9,50 Chute tous les 65 -

Stella, San Carlo All'arena, Vomero, Arenella, Miano, Secondigliano, San Pietro, a Patierno, Piscinola, Scampia, Chiaiano) Alimentari
AREA CENTRO NORD - III - V- VII - VIII MUNICIPALITÀ - STELLA, SAN CARLO ALL'ARENA, VOMERO, ARENELLA, MIANO, SECONDIGLIANO, SAN PIETRO, A PATIERNO, PISCINOLA, SCAMPIA, CHIAIANO) ALIMENTARI DAL 1° ALL'8 E DAL 24 AL 31 AGOSTO CON ORARIO AL BUONGUSTAIO CORSO ITALIA 107 8-14 E 16-20 ALIMENTARI SETTE A.S.R.L. VIA SUAREZ, 3/A CHIUSO 15 E 16 AGOSTO ALIMENTARI CASSESE VIA ROSAROLL, 101 CHIUSO DAL 12 AL 20 AGOSTO ALIMENTARI CIRIELLO AGOSTINO VIA G. A. PASQUALE, 10 CHIUSO DAL 9 AL 17 AGOSTO ALIMENTARI PANNA 2 S.R.L. VIA DOMENICO FONTANA, 1/3 CHIUSO DAL 15 AL 17 AGOSTO AMODIO SALUMERIA VIA LUCA GIORDANO – LATO PIAZZA DEGLI ARTISTI SEMPRE APERTO ARCESE GIUSEPPE VIA VERGINI 4 DAL 1° ALL'11 E DAL 16 AL 31 AGOSTO. ARUTA COSIMO SRL CORSO SECONDIGLIANO 382 SEMPRE APERTI CON ORARIO 8-14 BURRACCIONE GIUSEPPE VIA ARENA SANITÀ 25 SEMPRE APERTI CON ORARIO 8-14 CAROLA SALVATORE VIA STELLA 147 DAL 1° AL 13 E DAL 23 AL 31 AGOSTO. DAL 1° AL 9 E DAL 24 AL 31 AGOSTO CON ORARIO CARRIERO SALVATORE VIA CISTERNA DELL'OLIO 34 8-14 E 16-20 SEMPRE APERTI CON ORARIO 8-14 . CHIUSI 15 E CASALE SALUMERIA SNC VIA GEMITO 92 16 AGOSTO. DAL 1° AL 14 E DAL 28 AL 31 AGOSTO CON ORARIO CERINO CARLO PIAZZA CARLO III 46 CONTINUO DAL 1° ALL'8 E DAL 23 AL 31 AGOSTO CON ORARIO COPPOLA ANTONIO VIA ALTAMURA 19 8-14 E 16-20 DAL 1° AL 13 E DAL 23 AL 30 AGOSTO CON ORARIO COTUGNO CARLO VIA SEVERINO 6 8-14 DAL 1° AL 14 E DAL 24 AL 31 AGOSTO CON ORARIO DE MARTINO GIUSEPPE VIA MELLONI MACEDONIO 29 8-14 E 16-20 DAL 1° ALL'8 CON ORARIO 8-14 E DAL 24 AL 31 DELL'AVERSANO SALVATORE VIA CARAVAGLIOS 2 AGOSTO CON ORARIO 8-14 E 16-20 DESPAR VIA BERNINI – ADIACENZE CINEMA PLAZA SEMPRE APERTI DAL 1° AL 14 E DAL 23 AL 31 AGOSTO CON ORARIO DIANO RAFFAELA VIA DELLO STELVIO 52 8-14 E 16-20 SEMPRE APERTI CON ORARIO 8-20,30.IL 15 DÌPERDÌ NAPOLI - VIA ARANGIO RUIZ, 65 A AGOSTO APERTI CON ORARIO 8-14 E 16,30-20,30. -

Riferimenti Degli Enti Cui Sono Affidate Le Attivita' E Dei Csst
AZIONI DI SOSTEGNO EDUCATIVO E PERCORSI FORMATIVI TEORICI/PRATICI RIVOLTE AD ADOLESCENTI – DOTE COMUNE A seguito di apposito Avviso pubblico emanato con Determinazione Dirigenziale n. 24 del 15/06/16 per l’affidamento delle attività denominate "Azioni di sostegno educativo e percorsi formativi teorici/pratici rivolti ad adolescenti – Dote comune", con Disposizione Dirigenziale n. 55 del 05/12/16 sono state affidate le attività agli Enti di seguito indicati in tabella per la durata di 12 mesi aumentata fino ad un massimo di 16 mesi. ENTE MUNICIPALITA’ CSST ISTITUTO SALESIANO ERNESTO MENECHINI 3 - 5 Stella, Vomero, Arenella Miano, San Pietro a Patierno, Secondigliano, COOPERATIVA SOCIALE L'UOMO E IL LEGNO 7 - 8 Piscinola,Chiaiano, Scampia COOPERATIVA SOCIALE L'ORSA MAGGIORE 9 - 10 Soccavo, Pianura, Fuorigrotta, Bagnoli RIFERIMENTI DEGLI ENTI CUI SONO AFFIDATE LE ATTIVITA’ E DEI CSST RIFERI- ENTE COORDINATORE E-MAIL ENTE TEL. ENTE PEC ENTE CSST MAIL CSST MENTO GESTORE TERRITO RIALE MUNICIPALITA’ ISTITUTO MARIO DEL PIANO donvannisdb@ 0817511340 Istitutoe.menichini@pe Stella [email protected] 3 – 5 SALESIANO libero.it c.it li.it ERNESTO MENECHINI Vomero [email protected] Arenella [email protected] MUNICIPALITA’ COOPERATI PIRAS STEFANIA info@luomoeil 0815435924 coopluomoeillegno@leg Miano [email protected] 7 – 8 VA SOCIALE legno.com almail.it L'UOMO E San Pietro [email protected] IL LEGNO apoli.it Secondiglia [email protected]. no it Piscinola [email protected] Chiaiano [email protected] Scampia [email protected] MUNICIPALITA’ COOPERATI FRANCESCA francesca.don 0817281705 [email protected] Soccavo [email protected] 9 – 10 VA SOCIALE D’ONOFRIO ofrio2@gmail. -

Napoli-Per-Quartiere-P.-1-11.Pdf
bisogna vedere di nuovo quel che ‘‘ si è già visto, vedere in primavera quel che si è visto in estate, vedere di giorno quel che si è visto di notte, con il sole dove la prima volta pioveva... bisogna ritornare sui passi già dati per tracciarvi a fianco nuovi cammini [josé saramago] a giancarlo alisio napoliperquartiere chiaja / posillipo, fuorigrotta, bagnoli / san ferdinando / san giuseppe / san lorenzo / porto, pendino, mercato / vicaria, poggioreale / stella, san carlo all’arena / avvocata, montecalvario / vomero, arenella napoli per quartiere terza edizione aggiornata chiuso in redazione nel mese di febbraio 2019 coordinamento editoriale maria sapio art director enrica d’aguanno redazione e aggiornamenti alessandra guadagno impaginazione francesca aletto cartografia franco grieco fotografie mario milo napoli per quartiere: istruzioni per l’uso il confine dei dieci quartieri – da occidente, chiaja e posillipo, all’area orientale e collinare, vicaria, poggioreale, vomero e are- nella – rielabora l’accorpamento comunale ufficiale, relativamente recente, in municipalità, mantenendo viva per quanto possibile la memoria dei territori in cui ha preso forma, negli ultimi due secoli l’identità civile delle comunità residenti. nelle note di apertura, capitolo per capitolo, oltre al rinvio preci- so alla “municipalità”, vengono sintetizzati i dati e le informazioni essenziali per la vita quotidiana: estensione territoriale, abitanti, sicurezza e salute, trasporti. una mappa aggiornata mette in risalto il perimetro selezionato, i percorsi suggeriti, i principali collegamenti e le aree verdi. le informazioni di corredo, nelle colonne laterali, riportano pun- tualmente i riferimenti essenziali ‘per l’uso’: recapiti, orari di visita, didascalie delle illustrazioni [in azzurro], con rinvio alle pagine di riferimento nel volume; l’utilizzo del colore evidenzia, per comodità di lettura, le ‘macrocategorie’ di appartenenza: arti e monumenti, parchi e giardini, tempo libero/shopping. -

Together Is Better!
Together is better! By Br. Enrico Muller, FSC (Scampia, Italy) As a Lasallian community and as Lasallian educational ministries, the Lasallian cooperative Occhi Aperti (Open Eyes) and the association Arrevutammoce, we found ourselves, like everyone else, affected and overwhelmed by the pandemic. Like all of us we experienced fear, frustration, estrangement, silence… but the voices of the people that the Lord has placed beside us and to whom He has entrusted us brought us back to the reality of our call that must permeate and shape our lives as Christians and Lasallians. As a Community we immediately set to work with the Sisters of Providence of Father Scrosoppi, the Jesuits, the Chi Rom and Chi No and Magma Associations to respond to the needs of our Roma brothers and sisters and beyond. The group we created is called BAM, Brigata dell’Appoggio Mutuo (Brigade of Mutual Support) and in recent months has distributed food parcels for the Roma families of Scampia and Secondigliano, and for Neapolitan families, 1400 people, every 10/12 days or so, all finding among our friends and crowdfunding campaigns the necessary funds to buy food, detergents and everything needed for children 0-2 years. The action of our Lasallian community has always turned to the Roma of Giugliano in Campania, a town about 7 kilometers from Scampia; there are about 150 families, all very large and we have managed to make three distributions of food and personal cleaning materials. Occhi Aperti is also accompanying the students of the second chance school “IO VALGO” (I’m Worth) to the license exam with distance teaching so that the students can prepare the thesis they have to present at the end of this unusual school year. -
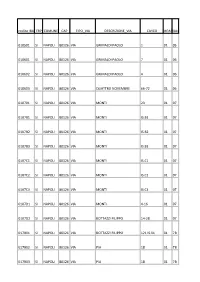
Codice IBU ERP COMUNE CAP TIPO VIA DESCRIZIONE VIA CIVICO COMPARTOSTRALCIO
codice IBU ERP COMUNE CAP TIPO_VIA DESCRIZIONE_VIA CIVICO COMPARTOSTRALCIO 010501 SI NAPOLI 80126 VIA GRIMALDI PAOLO 1 01 05 010601 SI NAPOLI 80126 VIA GRIMALDI PAOLO 7 01 06 010602 SI NAPOLI 80126 VIA GRIMALDI PAOLO 4 01 06 010603 SI NAPOLI 80126 VIA QUATTRO NOVEMBRE 66-72 01 06 010701 SI NAPOLI 80126 VIA MONTI 23 01 07 0107B1 SI NAPOLI 80126 VIA MONTI IS.B1 01 07 0107B2 SI NAPOLI 80126 VIA MONTI IS.B2 01 07 0107B3 SI NAPOLI 80126 VIA MONTI IS.B3 01 07 0107C1 SI NAPOLI 80126 VIA MONTI IS.C1 01 07 0107C2 SI NAPOLI 80126 VIA MONTI IS.C2 01 07 0107C3 SI NAPOLI 80126 VIA MONTI IS.C3 01 07 0107D1 SI NAPOLI 80126 VIA MONTI 4-16 01 07 0107D2 SI NAPOLI 80126 VIA BOTTAZZI FILIPPO 14-28 01 07 017B01 SI NAPOLI 80126 VIA BOTTAZZI FILIPPO 121 IS.01 01 7B 017B02 SI NAPOLI 80126 VIA PIA 18 01 7B 017B03 SI NAPOLI 80126 VIA PIA 18 01 7B 017B04 SI NAPOLI 80126 VIA BOTTAZZI FILIPPO 107-113 01 7B 017B05 SI NAPOLI 80126 VIA PIA IS.05 01 7B 017S0T NO NAPOLI 80147 VIA VELOTTI EGIDIO 18 01R203 SI NAPOLI 80126 VIA VICINALE CROCE DI PIPERNO PEGASO 01 R2 01R204 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO ANTARES 01 R2 01R205 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO ALPHA 01 R2 01R206 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO CENTAURO 01 R2 01R207 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO ERCOLE 01 R2 01R208 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO RIGEL 01 R2 01R209 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO ROSS 01 R2 01R210 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO WOLF 01 R2 01R211 SI NAPOLI 80126 VIA ENEIDE ORIONE 01 R2 01R2E1 SI NAPOLI 80126 VIA VICINALE PALAZZIELLO -

Gesac Tariffe Montaggio Lingue
Cyan - Magenta - ORO - Nero TAXI C.P. N° COMUNE DI NAPOLI – VII DIREZIONE CENTRALE TARIFFE PREDETERMINATE Euro PER INFORMAZIONI O RECLAMI: L’utente può scegliere le seguenti tariffe predeterminate e deve richiederle ad inizio corsa Servizio programmazione, Promozione e Controllo URBANE Servizi di Trasporto Pubblico Alberghi lungomare -- Aeroporto di Capodichino o viceversa 19,00 Galleria Principe di Napoli - Piazza Museo Nazionale Aliscafi Mergellina -- Aeroporto di Capodichino o viceversa 19,00 ITALIANO 80135 NAPOLI Stazione Centrale (Alberghi limitrofi) -- Aeroporto di Capodichino o viceversa 12,50 Tel. 081 5441401 - fax 081 5642209 COMUNE DI NAPOLI email : [email protected] Museo Capodimonte -- Museo S. Martino o viceversa 9,50 Piazza Municipio (Alberghi limitrofi) -- Museo Capodimonte o viceversa 9,50 TARIFFA ORDINARIA URBANA Aeroporto di Capodichino -- Alberghi Vomero - Fuorigrotta o viceversa 19,00 Piazza Municipio (Alberghi limitrofi) -- Aeroporto di Capodichino o viceversa 16,00 INIZIO CORSA Stazione Centrale -- Aliscafi mergellina o viceversa 12,50 Feriale dalle ore 7,00 alle ore 22,00 3,00 Stazione Centrale -- Alberghi Fuorigrotta o viceversa 16,00 Festiva dalle ore 7,00 alle ore 22,00 5,50 Stazione Mergellina -- Alberghi Fuorigrotta o viceversa 9,50 Notturna feriale o festiva dalle ore 22,00 alle ore 07,00 5,50 Stazione Mergellina -- Alberghi Agnano o viceversa 12,50 Corsa minima feriale dalle ore 7,00 alle ore 22,00 4,50 Molo Beverello -- Stazione centrale o viceversa 9,50 Scatto al tassametro ogni 65 metri 0,05