DOCSLIB.ORG

Linear Algebra I: Vector Spaces A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Linear Algebra I: Vector Spaces A Linear Algebra I: Vector Spaces A 1 Vector spaces and subspaces 1.1 Let F be a field (in this book, it will always be either the field of reals R or the field of complex numbers C). A vector space V D .V; C; o;˛./.˛2 F// over F is a set V with a binary operation C, a constant o and a collection of unary operations (i.e. maps) ˛ W V ! V labelled by the elements of F, satisfying (V1) .x C y/ C z D x C .y C z/, (V2) x C y D y C x, (V3) 0 x D o, (V4) ˛ .ˇ x/ D .˛ˇ/ x, (V5) 1 x D x, (V6) .˛ C ˇ/ x D ˛ x C ˇ x,and (V7) ˛ .x C y/ D ˛ x C ˛ y. Here, we write ˛ x and we will write also ˛x for the result ˛.x/ of the unary operation ˛ in x. Often, one uses the expression “multiplication of x by ˛”; but it is useful to keep in mind that what we really have is a collection of unary operations (see also 5.1 below). The elements of a vector space are often referred to as vectors. In contrast, the elements of the field F are then often referred to as scalars. In view of this, it is useful to reflect for a moment on the true meaning of the axioms (equalities) above. For instance, (V4), often referred to as the “associative law” in fact states that the composition of the functions V ! V labelled by ˇ; ˛ is labelled by the product ˛ˇ in F, the “distributive law” (V6) states that the (pointwise) sum of the mappings labelled by ˛ and ˇ is labelled by the sum ˛ C ˇ in F, and (V7) states that each of the maps ˛ preserves the sum C. See Example 3 in 1.2. I. Kriz and A. Pultr, Introduction to Mathematical Analysis, 451 DOI 10.1007/978-3-0348-0636-7, © Springer Basel 2013 452 A Linear Algebra I: Vector Spaces 1.2 Examples Vector spaces are ubiquitous. We present just a few examples; the reader will certainly be able to think of many more. 1. The n-dimensional row vector space Fn. The elements of Fn are the n-tuples .x1;:::;xn/ with xi 2 F, the addition is given by .x1;:::;xn/ C .y1;:::;yn/ D .x1 C y1;:::;xn C yn/; o D .0;:::;0/,andthe˛’s operate by the rule ˛..x1;:::;xn// D .˛x1;:::;˛xn/: Note that F1 can be viewed as the F. However, although the operations acome from the binary multiplication in F, their role in a vector space is different. See 5.1 below. 2. Spaces of real functions.ThesetF.M/ of all real functions on a set M , with pointwise addition and multiplication by real numbers is obviously a vector space over R. Similarly, we have the vector space C.J/ of all the continuous functions on an interval J , or e.g. the space C 1.J / of all continuously differentiable functions on an open interval J or the space C 1.J / of all smooth functions on J , i.e. functions which have all higher derivatives. There are also analogous C-vector spaces of complex functions. 3. Let V be the set of positive reals. Define x ˚ y D xy, o D 1, and for arbitrary ˛ 2 R, ˛ x D x˛.Then.V; ˚; o;˛ ./.˛ 2 R// is a vector space (see Exercise (1)). 1.3 An important convention We have distinguished above the elements of the vector space and the elements of the field by using roman and greek letters. This is a good convention for a definition, but in the row vector spaces Fn, which will play a particular role below, it is somemewhat clumsy. Instead, we will use for an arithmetic vector a bold-faced variant of the letter denoting the coordinates. Thus, x D .x1;:::;xn/; a D .a1;:::;an/; etc. Similarly we will write f D .f1;:::;fn/ for the n-tuple of functions fj W X ! R resp. C (after all, they can be viewed as mappings f W X ! Fn), and similarly. 1 Vector spaces and subspaces 453 These conventions make reading about vectors much easier, and we will maintain them as long as possible (for example in our discussion of multivariable differential calculus in Chapter 3). The fact is, however, that in certain more advanced settings the conventions become cumbersome or even ambiguous (for example in the context of tensor calculus in Chapter 15), and because of this, in the later chapters of this book we eventually abandon them, as one usually does in more advanced topics of analysis. We do, however, use the symbol o universally for the zero element of a general vector space – so that in Fn we have o D .0;0;:::;0/. 1.4 We have the following trivial Observation. In any vector space V , for all x 2 V , we have x C o D x and there exists precisely one y such that x C y D o, namely y D .1/x. (Indeed, x C o D 1 x C 0 x D .1 C 0/x D x and x C .1/x D 1x C .1/x D .1 C .1//x D 0 x D o,andifx C y D o and x C z D o then y D y C .x C z/ D .y C x/ C z D z.) 1.5 (Vector) subspaces A subspace of a vector space V is a subset W  V that is itself a vector space with the operations inherited from V . Since the equations required in V hold for special as well as general elements, we have a trivial Observation. A subset W  V of a vector space is a subspace if and only if (a) o 2 W , (b) if x;y 2 W then x C y 2 W , and (c) for all ˛ 2 F and x 2 W , ˛x 2 W . 1.5.1 Also the following statement is immediate. Proposition. The intersection of an arbitrary set of subspaces of a vector space V is a subspace of V . 1.6 Generating sets By 1.5.1, we see that for each subset M of V there exists the smallest subspace W  V containing M , namely 454 A Linear Algebra I: Vector Spaces \ L.M / D fW j W subspace of V and M  W g: For M finite, we use the notatiom L.u1;:::;un/ instead of L.fu1;:::;ung/: Obviously L.;/ Dfog. We say that M generates L.M /; in particular if L.M / D V we say that M is a generating set (of V ). One often speaks of a set of generators but we have to keep in mind that this does not imply each of its elements generates V , which would be a much stronger statement. If there exists a finite generating system we say that V is finitely generated,or finite-dimensional. 1.7 The sum of subspaces Let W1;W2 be subspaces. Unlike the intersection W1 \ W2, the union W1 [ W2 is generally (and typically) not a subspace. But we have the smallest subspace containing both W1 and W2, namely L.W1 [ W2/. It will be denoted by W1 C W2 and called the sum of W1 and W2. (One often uses the symbol ‘˚’ instead of ‘C’ when one also has W1 \ W2 Dfog.) 2 Linear combinations, linear independence 2.1 A linear combination of a system x1;:::;xn of elements of a vector space V over F is a formula Xn ˛1x1 CC˛nxn (briefly, ˛j xj /: (*) j D1 The “system” in question is to be understood as the sequence, although the order in which it is presented will play no role. However, a possible repetition of an individual element is essential. Note that we spoke of (*) as of a “formula”. That is, we had in mind the full information involved (more pedantically, we could speak of the linear combination as of the sequence together with the mapping f1;:::;ng!F sending j to ˛j ). The vector obtained as the result of the indicated operations should be referred to as the result of the linear combination (*). We will follow this convention consistently 2 Linear combinations, linear independence 455 Xn to begin with; later, we will speak of a linear combination ˛j xj more loosely, j D1 trusting that the reader will be able to tell from the context whether we will mean the explicit formula or its result. 2.2 A linear combination (*)issaidtobenon-trivial if at least one of the ˛j is non-zero. Asystemx1;:::;xn is linearly dependent if there exists a non-trivial linear combination (*) with result o. Otherwise, we speak of a linearly independent system. 2.2.1 Proposition. 1. If x1;:::;xn is linearly dependent resp. independent then for any permutation of f1;:::;ng the system x.1/;:::;x.n/ is linearly dependent resp. independent. 2. A subsystem of a linearly independent system is linearly independent. 3. Let ˇ2;:::;ˇn be arbitrary. Then x1 :::;xn is linearly independent if and only if Xn the system x1 C ˇj xj ;x2;:::;xn is. j D2 4. A system x1;:::;xn is linearly dependent if and only if some of its members are a (result of a) linear combination of the others. In particular, any system containing o is linearly dependent. Similarly, if there exist j ¤ k such that xj D xk then x1;:::;xn is linearly dependent.
Load more

Recommended publications
  • 2 Hilbert Spaces You Should Have Seen Some Examples Last Semester
    2 Hilbert spaces You should have seen some examples last semester. The simplest (finite-dimensional) ex- C • A complex Hilbert space H is a complete normed space over whose norm is derived from an ample is Cn with its standard inner product. It’s worth recalling from linear algebra that if V is inner product. That is, we assume that there is a sesquilinear form ( , ): H H C, linear in · · × → an n-dimensional (complex) vector space, then from any set of n linearly independent vectors we the first variable and conjugate linear in the second, such that can manufacture an orthonormal basis e1, e2,..., en using the Gram-Schmidt process. In terms of this basis we can write any v V in the form (f ,д) = (д, f ), ∈ v = a e , a = (v, e ) (f , f ) 0 f H, and (f , f ) = 0 = f = 0. i i i i ≥ ∀ ∈ ⇒ ∑ The norm and inner product are related by which can be derived by taking the inner product of the equation v = aiei with ei. We also have n ∑ (f , f ) = f 2. ∥ ∥ v 2 = a 2. ∥ ∥ | i | i=1 We will always assume that H is separable (has a countable dense subset). ∑ Standard infinite-dimensional examples are l2(N) or l2(Z), the space of square-summable As usual for a normed space, the distance on H is given byd(f ,д) = f д = (f д, f д). • • ∥ − ∥ − − sequences, and L2(Ω) where Ω is a measurable subset of Rn. The Cauchy-Schwarz and triangle inequalities, • √ (f ,д) f д , f + д f + д , | | ≤ ∥ ∥∥ ∥ ∥ ∥ ≤ ∥ ∥ ∥ ∥ 2.1 Orthogonality can be derived fairly easily from the inner product.
    [Show full text]
  • The Integral Geometry of Line Complexes and a Theorem of Gelfand-Graev Astérisque, Tome S131 (1985), P
    Astérisque VICTOR GUILLEMIN The integral geometry of line complexes and a theorem of Gelfand-Graev Astérisque, tome S131 (1985), p. 135-149 <http://www.numdam.org/item?id=AST_1985__S131__135_0> © Société mathématique de France, 1985, tous droits réservés. L’accès aux archives de la collection « Astérisque » (http://smf4.emath.fr/ Publications/Asterisque/) implique l’accord avec les conditions générales d’uti- lisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ Société Mathématique de France Astérisque, hors série, 1985, p. 135-149 THE INTEGRAL GEOMETRY OF LINE COMPLEXES AND A THEOREM OF GELFAND-GRAEV BY Victor GUILLEMIN 1. Introduction Let P = CP3 be the complex three-dimensional projective space and let G = CG(2,4) be the Grassmannian of complex two-dimensional subspaces of C4. To each point p E G corresponds a complex line lp in P. Given a smooth function, /, on P we will show in § 2 how to define properly the line integral, (1.1) f(\)d\ d\. = f(p). d A complex hypersurface, 5, in G is called admissible if there exists no smooth function, /, which is not identically zero but for which the line integrals, (1,1) are zero for all p G 5. In other words if S is admissible, then, in principle, / can be determined by its integrals over the lines, Zp, p G 5. In the 60's GELFAND and GRAEV settled the problem of characterizing which subvarieties, 5, of G have this property.
    [Show full text]
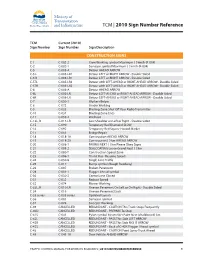
  • 2010 Sign Number Reference for Traffic Control Manual
    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
    [Show full text]
  • 18.06 Linear Algebra, Problem Set 5 Solutions
    18.06 Problem Set 5 Solution Total: points Section 4.1. Problem 7. Every system with no solution is like the one in problem 6. There are numbers y1; : : : ; ym that multiply the m equations so they add up to 0 = 1. This is called Fredholm’s Alternative: T Exactly one of these problems has a solution: Ax = b OR A y = 0 with T y b = 1. T If b is not in the column space of A it is not orthogonal to the nullspace of A . Multiply the equations x1 − x2 = 1 and x2 − x3 = 1 and x1 − x3 = 1 by numbers y1; y2; y3 chosen so that the equations add up to 0 = 1. Solution (4 points) Let y1 = 1, y2 = 1 and y3 = −1. Then the left-hand side of the sum of the equations is (x1 − x2) + (x2 − x3) − (x1 − x3) = x1 − x2 + x2 − x3 + x3 − x1 = 0 and the right-hand side is 1 + 1 − 1 = 1: Problem 9. If AT Ax = 0 then Ax = 0. Reason: Ax is inthe nullspace of AT and also in the of A and those spaces are . Conclusion: AT A has the same nullspace as A. This key fact is repeated in the next section. Solution (4 points) Ax is in the nullspace of AT and also in the column space of A and those spaces are orthogonal. Problem 31. The command N=null(A) will produce a basis for the nullspace of A. Then the command B=null(N') will produce a basis for the of A.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • Final Exam Outline 1.1, 1.2 Scalars and Vectors in R N. the Magnitude
    Final Exam Outline 1.1, 1.2 Scalars and vectors in Rn. The magnitude of a vector. Row and column vectors. Vector addition. Scalar multiplication. The zero vector. Vector subtraction. Distance in Rn. Unit vectors. Linear combinations. The dot product. The angle between two vectors. Orthogonality. The CBS and triangle inequalities. Theorem 1.5. 2.1, 2.2 Systems of linear equations. Consistent and inconsistent systems. The coefficient and augmented matrices. Elementary row operations. The echelon form of a matrix. Gaussian elimination. Equivalent matrices. The reduced row echelon form. Gauss-Jordan elimination. Leading and free variables. The rank of a matrix. The rank theorem. Homogeneous systems. Theorem 2.2. 2.3 The span of a set of vectors. Linear dependence. Linear dependence and independence. Determining n whether a set {~v1, . ,~vk} of vectors in R is linearly dependent or independent. 3.1, 3.2 Matrix operations. Scalar multiplication, matrix addition, matrix multiplication. The zero and identity matrices. Partitioned matrices. The outer product form. The standard unit vectors. The transpose of a matrix. A system of linear equations in matrix form. Algebraic properties of the transpose. 3.3 The inverse of a matrix. Invertible (nonsingular) matrices. The uniqueness of the solution to Ax = b when A is invertible. The inverse of a nonsingular 2 × 2 matrix. Elementary matrices and EROs. Equivalent conditions for invertibility. Using Gauss-Jordan elimination to invert a nonsingular matrix. Theorems 3.7, 3.9. n n n 3.5 Subspaces of R . {0} and R as subspaces of R . The subspace span(v1,..., vk). The the row, column and null spaces of a matrix.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Span, Linear Independence and Basis Rank and Nullity
    Remarks for Exam 2 in Linear Algebra Span, linear independence and basis The span of a set of vectors is the set of all linear combinations of the vectors. A set of vectors is linearly independent if the only solution to c1v1 + ::: + ckvk = 0 is ci = 0 for all i. Given a set of vectors, you can determine if they are linearly independent by writing the vectors as the columns of the matrix A, and solving Ax = 0. If there are any non-zero solutions, then the vectors are linearly dependent. If the only solution is x = 0, then they are linearly independent. A basis for a subspace S of Rn is a set of vectors that spans S and is linearly independent. There are many bases, but every basis must have exactly k = dim(S) vectors. A spanning set in S must contain at least k vectors, and a linearly independent set in S can contain at most k vectors. A spanning set in S with exactly k vectors is a basis. A linearly independent set in S with exactly k vectors is a basis. Rank and nullity The span of the rows of matrix A is the row space of A. The span of the columns of A is the column space C(A). The row and column spaces always have the same dimension, called the rank of A. Let r = rank(A). Then r is the maximal number of linearly independent row vectors, and the maximal number of linearly independent column vectors. So if r < n then the columns are linearly dependent; if r < m then the rows are linearly dependent.
    [Show full text]
  • Maxwell's Equations in Differential Form
    M03_RAO3333_1_SE_CHO3.QXD 4/9/08 1:17 PM Page 71 CHAPTER Maxwell’s Equations in Differential Form 3 In Chapter 2 we introduced Maxwell’s equations in integral form. We learned that the quantities involved in the formulation of these equations are the scalar quantities, elec- tromotive force, magnetomotive force, magnetic flux, displacement flux, charge, and current, which are related to the field vectors and source densities through line, surface, and volume integrals. Thus, the integral forms of Maxwell’s equations,while containing all the information pertinent to the interdependence of the field and source quantities over a given region in space, do not permit us to study directly the interaction between the field vectors and their relationships with the source densities at individual points. It is our goal in this chapter to derive the differential forms of Maxwell’s equations that apply directly to the field vectors and source densities at a given point. We shall derive Maxwell’s equations in differential form by applying Maxwell’s equations in integral form to infinitesimal closed paths, surfaces, and volumes, in the limit that they shrink to points. We will find that the differential equations relate the spatial variations of the field vectors at a given point to their temporal variations and to the charge and current densities at that point. In this process we shall also learn two important operations in vector calculus, known as curl and divergence, and two related theorems, known as Stokes’ and divergence theorems. 3.1 FARADAY’S LAW We recall from the previous chapter that Faraday’s law is given in integral form by d E # dl =- B # dS (3.1) CC dt LS where S is any surface bounded by the closed path C.In the most general case,the elec- tric and magnetic fields have all three components (x, y,and z) and are dependent on all three coordinates (x, y,and z) in addition to time (t).
    [Show full text]
  • CR Singular Immersions of Complex Projective Spaces
    Beitr¨agezur Algebra und Geometrie Contributions to Algebra and Geometry Volume 43 (2002), No. 2, 451-477. CR Singular Immersions of Complex Projective Spaces Adam Coffman∗ Department of Mathematical Sciences Indiana University Purdue University Fort Wayne Fort Wayne, IN 46805-1499 e-mail: Coff[email protected] Abstract. Quadratically parametrized smooth maps from one complex projective space to another are constructed as projections of the Segre map of the complexifi- cation. A classification theorem relates equivalence classes of projections to congru- ence classes of matrix pencils. Maps from the 2-sphere to the complex projective plane, which generalize stereographic projection, and immersions of the complex projective plane in four and five complex dimensions, are considered in detail. Of particular interest are the CR singular points in the image. MSC 2000: 14E05, 14P05, 15A22, 32S20, 32V40 1. Introduction It was shown by [23] that the complex projective plane CP 2 can be embedded in R7. An example of such an embedding, where R7 is considered as a subspace of C4, and CP 2 has complex homogeneous coordinates [z1 : z2 : z3], was given by the following parametric map: 1 2 2 [z1 : z2 : z3] 7→ 2 2 2 (z2z¯3, z3z¯1, z1z¯2, |z1| − |z2| ). |z1| + |z2| + |z3| Another parametric map of a similar form embeds the complex projective line CP 1 in R3 ⊆ C2: 1 2 2 [z0 : z1] 7→ 2 2 (2¯z0z1, |z1| − |z0| ). |z0| + |z1| ∗The author’s research was supported in part by a 1999 IPFW Summer Faculty Research Grant. 0138-4821/93 $ 2.50 c 2002 Heldermann Verlag 452 Adam Coffman: CR Singular Immersions of Complex Projective Spaces This may look more familiar when restricted to an affine neighborhood, [z0 : z1] = (1, z) = (1, x + iy), so the set of complex numbers is mapped to the unit sphere: 2x 2y |z|2 − 1 z 7→ ( , , ), 1 + |z|2 1 + |z|2 1 + |z|2 and the “point at infinity”, [0 : 1], is mapped to the point (0, 0, 1) ∈ R3.
    [Show full text]
  • Rotation Matrix - Wikipedia, the Free Encyclopedia Page 1 of 22
    Rotation matrix - Wikipedia, the free encyclopedia Page 1 of 22 Rotation matrix From Wikipedia, the free encyclopedia In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix rotates points in the xy -Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details). In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space. Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, i.e. an orthogonal matrix whose determinant is 1: . The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1. Contents 1 Rotations in two dimensions 1.1 Non-standard orientation
    [Show full text]
  • Some C*-Algebras with a Single Generator*1 )
    transactions of the american mathematical society Volume 215, 1976 SOMEC*-ALGEBRAS WITH A SINGLEGENERATOR*1 ) BY CATHERINE L. OLSEN AND WILLIAM R. ZAME ABSTRACT. This paper grew out of the following question: If X is a com- pact subset of Cn, is C(X) ® M„ (the C*-algebra of n x n matrices with entries from C(X)) singly generated? It is shown that the answer is affirmative; in fact, A ® M„ is singly generated whenever A is a C*-algebra with identity, generated by a set of n(n + l)/2 elements of which n(n - l)/2 are selfadjoint. If A is a separable C*-algebra with identity, then A ® K and A ® U are shown to be sing- ly generated, where K is the algebra of compact operators in a separable, infinite- dimensional Hubert space, and U is any UHF algebra. In all these cases, the gen- erator is explicitly constructed. 1. Introduction. This paper grew out of a question raised by Claude Scho- chet and communicated to us by J. A. Deddens: If X is a compact subset of C, is C(X) ® M„ (the C*-algebra ofnxn matrices with entries from C(X)) singly generated? We show that the answer is affirmative; in fact, A ® Mn is singly gen- erated whenever A is a C*-algebra with identity, generated by a set of n(n + l)/2 elements of which n(n - l)/2 are selfadjoint. Working towards a converse, we show that A ® M2 need not be singly generated if A is generated by a set con- sisting of four elements.
    [Show full text]