DOCSLIB.ORG

I a HIGH-ALTITUDE NUCLEAR ENVIRONMENT SIMULATION By

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
I a HIGH-ALTITUDE NUCLEAR ENVIRONMENT SIMULATION By A HIGH-ALTITUDE NUCLEAR ENVIRONMENT SIMULATION by RYAN D. WHITE B.S., Kansas State University, 2008 A THESIS submitted in partial fulfillment of the requirements for the degree MASTER OF SCIENCE Department of Mechanical and Nuclear Engineering College of Engineering KANSAS STATE UNIVERSITY Manhattan, Kansas 2009 Approved by: Major Professor Dr. Kenneth Shultis i Abstract A program which calculates the radiation dosage to a predetermined set of components inside of a kill vehicle as a result of natural or artificial radiation sources has been developed for use within the confines of a parent external simulation. This dose can then be used to determine if a critical component has malfunctioned or failed completely, thereby rendering the interceptor unable to finish its mission. Knowledge of system and component performance as a function of incident high-energy particles leads to better battle management planning, CONOPS, and potentially a more efficient shielding design to achieve a higher probability of mission success. ii Table of Contents List of Figures................................................................................................................................ vi List of Tables ................................................................................................................................. ix CHAPTER 1 INTRODUCTION .............................................................................................. 1 1.1 Motivation for Present Work.......................................................................................... 1 1.2 Problem Overview.......................................................................................................... 2 1.3 Thesis Organization........................................................................................................ 3 CHAPTER 2 Sources of Radiation........................................................................................... 5 2.1 Natural Space Radiation ................................................................................................. 5 2.1.1 The AP8 and AE8 Models........................................................................................ 10 2.1.2 Limitations to the The AP8/AE8 Model................................................................... 13 2.2 Artificial Radiation Sources.......................................................................................... 14 2.2.1 Types of Artificial Radiation Associated with a Nuclear Burst ............................... 14 2.2.2 Flux Calculations ...................................................................................................... 16 2.2.3 Angle of Incidence.................................................................................................... 18 2.2.4 Atmospheric Attenuation of Particles....................................................................... 19 2.2.4.1 Line of Sight Calculations ................................................................................ 19 2.2.4.2 Method for Flux Attenuation ............................................................................ 23 2.2.4.3 Calculating Air Density at a Point .................................................................... 25 2.2.4.4 Integrating Air Density along a Line of Sight .................................................. 28 2.2.4.5 Limitations to the Atmospheric Models ........................................................... 32 2.2.4.6 Comments on the Atmospheric Attenuation Model ......................................... 35 2.2.5 Effects of Nuclear Bursts on Radiation Belts and Geomagnetic Fields ................... 36 2.2.5.1 The Starfish Prime Event.................................................................................. 36 2.2.5.2 The Magnetic Bubble........................................................................................ 38 2.2.5.3 Pumped Radiation Belts.................................................................................... 39 2.2.5.4 A Model for Radiation Belt Pumping............................................................... 41 2.3 Simulation Modeling Assumptions .............................................................................. 41 CHAPTER 3 Nature of the Program....................................................................................... 43 iii 3.1 Interface Assumption.................................................................................................... 43 3.2 How the Program Interacts with a Larger Simulation .................................................. 44 3.3 Simulation Model Inputs .............................................................................................. 46 3.3.1 Initial Inputs from a Larger Simulation .................................................................... 47 3.3.2 Running Inputs from a Larger Simulation................................................................ 47 3.3.3 List of Input Variables .............................................................................................. 48 3.4 Input File Formats......................................................................................................... 49 3.4.1 Interceptor Class Input Files..................................................................................... 50 3.4.2 Fission Class Input Files ........................................................................................... 51 3.5 Outputs to External Simulation..................................................................................... 51 3.6 Verification and Validation .......................................................................................... 51 CHAPTER 4 Recommended Enhancements .......................................................................... 53 4.1 Natural Radiation.......................................................................................................... 53 4.2 Artificial Radiation ....................................................................................................... 53 References..................................................................................................................................... 56 APPENDIX A MCNP Input File for Atmospheric Attenuation Testing .................................. 61 APPENDIX B Interceptor Class Definition ............................................................................. 63 B.1 Private Methods............................................................................................................ 63 B.2 Public Methods ............................................................................................................. 64 B.3 Private Members........................................................................................................... 66 B.4 Private Members........................................................................................................... 66 APPENDIX C Fission Class Definition.................................................................................... 67 C.1 Private Methods............................................................................................................ 67 C.2 Public Methods ............................................................................................................. 69 C.3 Private Members........................................................................................................... 73 C.4 Public Members............................................................................................................ 74 APPENDIX D FluxtoDose Class Definition............................................................................. 75 D.1 Private Methods............................................................................................................ 75 D.2 Public Methods ............................................................................................................. 77 D.3 Private Members........................................................................................................... 78 D.4 Public Members............................................................................................................ 78 iv APPENDIX E DoseMath Class Definition............................................................................... 79 E.1 Private Methods............................................................................................................ 79 E.2 Public Methods ............................................................................................................. 79 E.3 Private Members........................................................................................................... 80 E.4 Public Members............................................................................................................ 80 APPENDIX F VanAllen Class Definition................................................................................. 81 F.1 Private Methods............................................................................................................ 81 F.2 Public Methods ............................................................................................................. 83 F.3 Private Members........................................................................................................... 85 F.4 Public Members...........................................................................................................
Load more

Recommended publications
  • Grappling with the Bomb: Britain's Pacific H-Bomb Tests
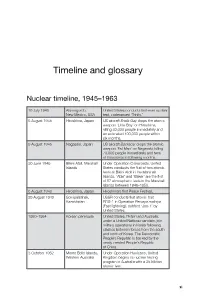
    Timeline and glossary Nuclear timeline, 1945–1963 16 July 1945 Alamogordo, United States conducts first-ever nuclear New Mexico, USA test, codenamed ‘Trinity .’ 6 August 1945 Hiroshima, Japan US aircraft Enola Gay drops the atomic weapon ‘Little Boy’ on Hiroshima, killing 80,000 people immediately and an estimated 100,000 people within six months . 9 August 1945 Nagasaki, Japan US aircraft Bockscar drops the atomic weapon ‘Fat Man’ on Nagasaki, killing 70,000 people immediately and tens of thousands in following months . 30 June 1946 Bikini Atoll, Marshall Under Operation Crossroads, United Islands States conducts the first of two atomic tests at Bikini Atoll in the Marshall Islands. ‘Able’ and ‘Baker’ are the first of 67 atmospheric tests in the Marshall Islands between 1946–1958 . 6 August 1948 Hiroshima, Japan Hiroshima’s first Peace Festival. 29 August 1949 Semipalatinsk, USSR conducts first atomic test Kazakhstan RDS-1 in Operation Pervaya molniya (Fast lightning), dubbed ‘Joe-1’ by United States . 1950–1954 Korean peninsula United States, Britain and Australia, under a United Nations mandate, join military operations in Korea following clashes between forces from the south and north of Korea. The Democratic People’s Republic is backed by the newly created People’s Republic of China . 3 October 1952 Monte Bello Islands, Under Operation Hurricane, United Western Australia Kingdom begins its nuclear testing program in Australia with a 25 kiloton atomic test . xi GRAPPLING WITH THE BOMB 1 November 1952 Bikini Atoll, Marshall United States conducts its first Islands hydrogen bomb test, codenamed ‘Mike’ (10 .4 megatons) as part of Operation Ivy .
    [Show full text]
  • Using a Nuclear Explosive Device for Planetary Defense Against an Incoming Asteroid
    Georgetown University Law Center Scholarship @ GEORGETOWN LAW 2019 Exoatmospheric Plowshares: Using a Nuclear Explosive Device for Planetary Defense Against an Incoming Asteroid David A. Koplow Georgetown University Law Center, [email protected] This paper can be downloaded free of charge from: https://scholarship.law.georgetown.edu/facpub/2197 https://ssrn.com/abstract=3229382 UCLA Journal of International Law & Foreign Affairs, Spring 2019, Issue 1, 76. This open-access article is brought to you by the Georgetown Law Library. Posted with permission of the author. Follow this and additional works at: https://scholarship.law.georgetown.edu/facpub Part of the Air and Space Law Commons, International Law Commons, Law and Philosophy Commons, and the National Security Law Commons EXOATMOSPHERIC PLOWSHARES: USING A NUCLEAR EXPLOSIVE DEVICE FOR PLANETARY DEFENSE AGAINST AN INCOMING ASTEROID DavidA. Koplow* "They shall bear their swords into plowshares, and their spears into pruning hooks" Isaiah 2:4 ABSTRACT What should be done if we suddenly discover a large asteroid on a collision course with Earth? The consequences of an impact could be enormous-scientists believe thatsuch a strike 60 million years ago led to the extinction of the dinosaurs, and something ofsimilar magnitude could happen again. Although no such extraterrestrialthreat now looms on the horizon, astronomers concede that they cannot detect all the potentially hazardous * Professor of Law, Georgetown University Law Center. The author gratefully acknowledges the valuable comments from the following experts, colleagues and friends who reviewed prior drafts of this manuscript: Hope M. Babcock, Michael R. Cannon, Pierce Corden, Thomas Graham, Jr., Henry R. Hertzfeld, Edward M.
    [Show full text]
  • Operation Dominic I
    OPERATION DOMINIC I United States Atmospheric Nuclear Weapons Tests Nuclear Test Personnel Review Prepared by the Defense Nuclear Agency as Executive Agency for the Department of Defense HRE- 0 4 3 6 . .% I.., -., 5. ooument. Tbe t k oorreotsd oontraofor that tad oa the book aw ra-ready c I I i I 1 1 I 1 I 1 i I I i I I I i i t I REPORT NUMBER 2. GOVT ACCESSION NC I NA6OccOF 1 i Technical Report 7. AUTHOR(.) i L. Berkhouse, S.E. Davis, F.R. Gladeck, J.H. Hallowell, C.B. Jones, E.J. Martin, DNAOO1-79-C-0472 R.A. Miller, F.W. McMullan, M.J. Osborne I I 9. PERFORMING ORGAMIIATION NWE AN0 AODRCSS ID. PROGRAM ELEMENT PROJECT. TASU Kamn Tempo AREA & WOW UNIT'NUMSERS P.O. Drawer (816 State St.) QQ . Subtask U99QAXMK506-09 ; Santa Barbara, CA 93102 11. CONTROLLING OFClCC MAME AM0 ADDRESS 12. REPORT DATE 1 nirpctor- . - - - Defense Nuclear Agency Washington, DC 20305 71, MONITORING AGENCY NAME AODRCSs(rfdIfI*mI ka CamlIlIU Olllc.) IS. SECURITY CLASS. (-1 ah -*) J Unclassified SCHCDULC 1 i 1 I 1 IO. SUPPLEMENTARY NOTES This work was sponsored by the Defense Nuclear Agency under RDT&E RMSS 1 Code 6350079464 U99QAXMK506-09 H2590D. For sale by the National Technical Information Service, Springfield, VA 22161 19. KEY WOROS (Cmlmm a nm.. mid. I1 n.c...-7 .nd Id.nllh 4 bled nlrmk) I Nuclear Testing Polaris KINGFISH Nuclear Test Personnel Review (NTPR) FISHBOWL TIGHTROPE DOMINIC Phase I Christmas Island CHECKMATE 1 Johnston Island STARFISH SWORDFISH ASROC BLUEGILL (Continued) D.
    [Show full text]
  • Bob Farquhar
    1 2 Created by Bob Farquhar For and dedicated to my grandchildren, their children, and all humanity. This is Copyright material 3 Table of Contents Preface 4 Conclusions 6 Gadget 8 Making Bombs Tick 15 ‘Little Boy’ 25 ‘Fat Man’ 40 Effectiveness 49 Death By Radiation 52 Crossroads 55 Atomic Bomb Targets 66 Acheson–Lilienthal Report & Baruch Plan 68 The Tests 71 Guinea Pigs 92 Atomic Animals 96 Downwinders 100 The H-Bomb 109 Nukes in Space 119 Going Underground 124 Leaks and Vents 132 Turning Swords Into Plowshares 135 Nuclear Detonations by Other Countries 147 Cessation of Testing 159 Building Bombs 161 Delivering Bombs 178 Strategic Bombers 181 Nuclear Capable Tactical Aircraft 188 Missiles and MIRV’s 193 Naval Delivery 211 Stand-Off & Cruise Missiles 219 U.S. Nuclear Arsenal 229 Enduring Stockpile 246 Nuclear Treaties 251 Duck and Cover 255 Let’s Nuke Des Moines! 265 Conclusion 270 Lest We Forget 274 The Beginning or The End? 280 Update: 7/1/12 Copyright © 2012 rbf 4 Preface 5 Hey there, I’m Ralph. That’s my dog Spot over there. Welcome to the not-so-wonderful world of nuclear weaponry. This book is a journey from 1945 when the first atomic bomb was detonated in the New Mexico desert to where we are today. It’s an interesting and sometimes bizarre journey. It can also be horribly frightening. Today, there are enough nuclear weapons to destroy the civilized world several times over. Over 23,000. “Enough to make the rubble bounce,” Winston Churchill said. The United States alone has over 10,000 warheads in what’s called the ‘enduring stockpile.’ In my time, we took care of things Mano-a-Mano.
    [Show full text]
  • 26E 1958 List of Artificial Radiation Belts
    List of artificial radiation belts - Wikipedia, the free encyclopedia Page 1 of 3 List of artificial radiation belts From Wikipedia, the free encyclopedia Artificial radiation belts are radiation belts that have been created by high altitude nuclear explosions. [1][2][3][4] List of Artificial Radiation Belts Yield Altitude Nation of Explosion Location Date (approximate) (km) Origin Johnston Island 1958-08- Hardtack Teak 3.8 megatons 76.8 United States (Pacific) 01 Hardtack Johnston Island 1958-08- 3.8 megatons 43 United States Orange (Pacific) 12 1958-08- Argus I South Atlantic 1-2 kilotons 200 United States 27 1958-08- Argus II South Atlantic 1-2 kilotons 256 United States 30 1958-09- Argus III South Atlantic 1-2 kilotons 539 United States 06 Johnston Island 1962-07- Starfish Prime 1.4 megatons 400 United States (Pacific) 09 1962-10- K-3 Kazakhstan 300 kilotons 290 USSR 22 1962-10- K-4 Kazakhstan 300 kilotons 150 USSR 28 1962-11- K-5 Kazakhstan 300 kilotons 59 USSR 01 The table above only lists those high-altitude nuclear explosions for which a reference exists in the open (unclassified) English-language scientific literature to persistent artificial radiation belts resulting from the explosion. The Starfish Prime radiation belt had, by far, the greatest intensity and duration of any of the artificial radiation belts.[1] The Starfish Prime radiation belt damaged the United States satellites Ariel 1, Traac, Transit 4B, Injun I and Telstar I. It also damaged the Soviet satellite Cosmos V. All of these satellites failed completely within
    [Show full text]
  • The Uncertain Consequences of Nuclear Weapons Use
    THE UNCERTAIN CONSEQUENCES OF NUCLEAR WEAPONS USE Michael J. Frankel James Scouras George W. Ullrich Copyright © 2015 The Johns Hopkins University Applied Physics Laboratory LLC. All Rights Reserved. NSAD-R-15-020 THE UNCERTAIN CONSEQUENCES OF NUCLEAR WEAPONS USE iii Contents Figures ................................................................................................................................................................................................ v Abstract ............................................................................................................................................................................................vii Overview ....................................................................................................................................................................1 Historical Context .....................................................................................................................................................2 Surprises ..................................................................................................................................................................................... 4 Enduring Uncertainties, Waning Resources ................................................................................................................10 Physical Effects: What We Know, What Is Uncertain, and Tools of the Trade .............................................. 12 Nuclear Weapons Effects Phenomena...........................................................................................................................13
    [Show full text]
  • Exploring the High-Altitude Nuclear Detonation and Magnetic Storms Mahmoud E Yousif* Department of Physics, the University of Nairobi, Nairobi, Kenya
    ics & Ae ys ro h sp p a o r c t e s T A e Yousif, J Astrophys Aerospace Technol 2014, 2:2 f c h o Journal of Astrophysics & n l o a DOI: 10.4172/2329-6542.1000105 l n o r g u y o J Aerospace Technology ISSN: 2329-6542 Research Article Open Access Exploring the High-altitude Nuclear Detonation and Magnetic Storms Mahmoud E Yousif* Department of Physics, The University of Nairobi, Nairobi, Kenya Abstract The High-altitude Nuclear Detonation (HND) experiments were carried between 1958/62 by both the United States of America (USA) and the former Union of Soviet Socialist Republics (USSR); the Starfish HND resulted in many phenomena, it discharged great amount of beta particles and debris, releasing intense gamma radiation which ionized atoms and molecules, resulting in Compton electrons and the production of Electromagnetic Pulse (EMP); the experiment also produced intense magnetic field, measured worldwide, with magnitude inversely proportional to square of the radial distance; the graph near the detonation center gave similar characteristics to the Magnetic Storms (MS); these characteristics were analyzed, whereas in both phenomenon, an External Magnetic Field-Moment (ExMFM) was produced; both the source and magnitude of the produced ExMFM were also analyzed and a mechanisms suggested for EMP production; characteristics regulating both phenomena are disclosed and elaborated from different perspectives; it is with hope that this will help in the process towards better understanding to some aspects related to the ExMF production in which if managed will be an advancement of the long awaited alternative renewable energy.
    [Show full text]
  • Electromagnetic Pulse - Nuclear EMP - Futurescience.Com
    Electromagnetic Pulse - Nuclear EMP - futurescience.com Nuclear Electromagnetic Pulse by Jerry Emanuelson Futurescience, LLC The topic of nuclear electromagnetic pulse (EMP) is very mysterious to most people, and it is quite commonly misunderstood. It is also the subject of a large amount of misinformation. (It is a persistent problem that many people want to ignore the science and make it into a political issue.) There are separate pages on EMP personal protection, Soviet nuclear EMP tests in 1962, and on other topics including a separate page of notes and technical references. Much of the information here describes the possible effects of EMP on the continental United States, but the information can be used to describe the effects on any industrialized country. In testimony before the United States Congress House Armed Services Committee on October 7, 1999, the eminent physicist Dr. Lowell Wood, in talking about Starfish Prime and the related EMP-producing nuclear tests in 1962, stated, "Most fortunately, these tests took place over Johnston Island in the mid-Pacific rather than the Nevada Test Site, or electromagnetic pulse would still be indelibly imprinted in the minds of the citizenry of the western U.S., as well as in the history books. As it was, significant damage was done to both civilian and military electrical systems throughout the Hawaiian Islands, over 800 miles away from ground zero. The origin and nature of this damage was successfully obscured at the time -- aided by its mysterious character and the essentially incredible truth." http://www.futurescience.com/emp.html (1 of 14) [3/23/2010 2:38:20 PM] Electromagnetic Pulse - Nuclear EMP - futurescience.com The Starfish Prime Nuclear Test from more than 800 miles away Although nuclear EMP was known since the earliest days of nuclear weapons testing, the magnitude of the effects of nuclear EMP were not known until a 1962 test of a thermonuclear weapon in space called the Starfish Prime test.
    [Show full text]
  • Starfish Prime
    The STARFISH Exo-atmospheric, High-altitude Nuclear Weapons Test E. G. Stassinopoulos NASA/Goddard Space Flight Center Emeritus To study the effects of nuclear weapons, the United States conducted a series of atmospheric test in 1958, as for example the HARDTACK series in the Pacific Ocean and the ARGUS series in the South Atlantic Ocean. Additional high altitude nuclear tests were later conducted within the FISHBOWL series in 1962. During those tests, the STARFISH PRIME device, with a yield of 1.4 megatons TNT equivalent, was exploded on July 9, 1962, at a very high altitude (approximately 400 km) over Johnston Island in the Pacific, about 700 miles southwest of Hawaii. This exo-atmospheric nuclear explosion released about 1029 energetic fission electrons into the magnetosphere, creating an artificial radiation belt and raising the intensity levels of the natural Van Allen Belt electron population in the inner zone by several orders of magnitude. This additional radiation increased the total ionizing dose incident on spacecraft flying at that time to critical levels, resulting in the loss of seven satellites within months after the test, primarily from solar cell damage. The first such failure due to total dose was the TELSTAR satellite, which was launched a day after STARFISH. It was estimated that the spacecraft experienced a total dose from the weapon test 100 times larger than expected. Initial predictions about the longevity of the STARFISH debris ranged from the overly optimistic of some months to the more realistic of a few years. Studies conducted in the late 1960s [1, 2, 3, 4] attempted to define the rate of decay with varying results.
    [Show full text]
  • Mar 2010 Newsletter
    United States Atmospheric & Underwater Atomic Weapon Activities National Association of Atomic Veterans, Inc. 1945 “TRINITY“ “Assisting America’s Atomic Veterans Since 1979” ALAMOGORDO, N. M. Website: www.naav.com E-mail: [email protected] 1945 “LITTLE BOY“ HIROSHIMA, JAPAN R. J. RITTER - Editor March, 2010 1945 “FAT MAN“ NAGASAKI, JAPAN 1946 “CROSSROADS“ BIKINI ISLAND 1948 “SANDSTONE“ ENEWETAK ATOLL 1951 “RANGER“ NEVADA TEST SITE 1951 “GREENHOUSE“ ENEWETAK ATOLL 1951 “BUSTER – JANGLE“ NEVADA TEST SITE 1952 “TUMBLER - SNAPPER“ NEVADA TEST SITE 1952 “IVY“ ENEWETAK ATOLL 1953 “UPSHOT - KNOTHOLE“ NEVADA TEST SITE 1954 “CASTLE“ BIKINI ISLAND 1955 “TEAPOT“ NEVADA TEST SITE 1955 “WIGWAM“ OFFSHORE SAN DIEGO 1955 “PROJECT 56“ NEVADA TEST SITE 1956 “REDWING“ ENEWETAK & BIKINI 1957 “PLUMBOB“ NEVADA TEST SITE 1958 “HARDTACK-I“ ENEWETAK & BIKINI 1958 “NEWSREEL“ JOHNSON ISLAND 1958 “ARGUS“ SOUTH ATLANTIC 1958 “HARDTACK-II“ NEVADA TEST SITE 1961 “NOUGAT“ NEVADA TEST SITE 1962 “DOMINIC-I“ CHRISTMAS ISLAND JOHNSON ISLAND 1965 “FLINTLOCK“ AMCHITKA, ALASKA 1969 “MANDREL“ AMCHITKA, ALASKA 1971 “GROMMET“ AMCHITKA, ALASKA 1974 “POST TEST EVENTS“ AMCHITKA, ALASKA ------------ A “THOR” ROCKET RISES FROM THE LAUNCH PAD ON JOHNSTON “ IF YOU WERE THERE, ISLAND DURING THE 1962 ( DOMINIC-I ) “FISHBOWL” TEST SERIES YOU ARE AN ATOMIC VETERAN “ The Newsletter for America’s Atomic Veterans COMMANDERS COMMENTS efforts. It is important to note that the Directors and Officers of NAAV dedicate their service to our Mission Statement without NAAV is now entering it’s 31st. year of assist- compensation. Our sole source of operating income is derived ing America’s Atomic-Veteran community in from annual membership dues and ( tax exempt ) contribu- the areas of obtaining proper documentation tions.
    [Show full text]
  • Tickling the Sleeping Dragon's Tail: Should We Resume Nuclear Testing?
    TICKLING THE SLEEPING DRAGON’S TAIL Should We Resume Nuclear Testing? National Security Report Michael Frankel | James Scouras | George Ullrich TICKLING THE SLEEPING DRAGON’S TAIL Should We Resume Nuclear Testing? Michael Frankel James Scouras George Ullrich Copyright © 2021 The Johns Hopkins University Applied Physics Laboratory LLC. All Rights Reserved. “Tickling the sleeping dragon’s tail” is a metaphor for risking severe consequences by taking an unnecessary provocative action. Its origin can be traced to the last year of the Manhattan Project at Los Alamos National Laboratory (LANL) in 1946. When investigating the critical mass of plutonium, LANL scientists usually brought two halves of a beryllium reflecting shell surrounding a fissile core closer together, observing the increase in reaction rate via a scintillation counter. They manually forced the two half-shells closer together by gripping them through a thumbhole at the top, while as a safety precaution, keeping the shells from completely closing by inserting shims. However, the habit of Louis Slotin was to remove the shims and keep the shells separated by manually inserting a screwdriver. Enrico Fermi is reported to have warned Slotin and others that they would be “dead within a year” if they continued this procedure. One day the screwdriver slipped, allowing the two half-shells to completely close, and the increased reflectivity drove the core toward criticality. Slotin immediately flipped the top half-shell loose with a flick of the screwdriver, but by then he had endured
    [Show full text]
  • Comprehensive Nuclear-Test-Ban Treaty: Contributing Towards a World Free of Nuclear Weapons by Jean Du Preez 1
    2016-2017 Critical Issues Forum (CIF) Comprehensive Nuclear-Test-Ban Treaty: Contributing towards a World Free of Nuclear Weapons by Jean du Preez 1. History of Nuclear Testing, Nuclear Testing and the Arms Race 5. Educational resources to train the next generation of CTBT experts “If the radiance of a thousand suns were to burst at once into the sky, that would be like the splendor of the mighty one. Now I am become Death, the destroyer of worlds“ From the Hindu scripture Bhagavad Gita as recalled by Dr Robert Oppenheimer Trinity test: 16 July 1945 https://www.youtube.com/watch?v=ZuRvBoLu4t0 Absolute Devastation: Hiroshima & Nagasaki Hiroshima Nagasaki 6 August 1945- “Little Boy” 9 August 1945- “Fat Man” 118,000 killed, 80,000 wounded 74,000 killed, 75,000 wounded The Destruction of Hiroshima bomb (13Kt) • 0-1.0 km: 86% killed • 1-2.5 km: 27% killed • 0-1.3 km: prompt radiation zone • 0-2.1 km: 3rd degree burns • 0-2.7 km: 2nd degree burns Heat: 6000 degrees Celcius • 0-0.3 km: 50 psi overpressure – destroys everything • 0-0.7 km: 10 psi - sweep everything in a high-rise building onto streets • 0-1.2 – 1.6 km: 3 - 5 psi - destroy brick houses & shatter windowpanes Testing and the start of the nuclear arms race Trinity Test (20 kt) UK USSR Tsar Bomba USSR JOE Hurricane (57 mt) (22 kt) (25 kt) China tests at Lop Nur 1945 1949 1952 1961 1964 1960 1962 1974 US Mike Hiroshima & (10.4 mt) Blue Little Feller Nagasaki (Davy Crockett) Dessert Rat (0.01 – 0.02 kt) Smiling France test Budha in Algeria (12Kt): India 70Kt For more on nuclear testing over time, see the CTBTO website Scale comparison U.S.
    [Show full text]