Structures of the 2:1 Layers of Pyrophyllite and Talc
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Phase Equilibria and Thermodynamic Properties of Minerals in the Beo
American Mineralogist, Volwne 71, pages 277-300, 1986 Phaseequilibria and thermodynamic properties of mineralsin the BeO-AlrO3-SiO2-H2O(BASH) system,with petrologicapplications Mlnx D. B.qnroN Department of Earth and SpaceSciences, University of California, Los Angeles,Los Angeles,California 90024 Ansrru,cr The phase relations and thermodynamic properties of behoite (Be(OH)r), bertrandite (BeoSirOr(OH)J, beryl (BerAlrSiuO,r),bromellite (BeO), chrysoberyl (BeAl,Oo), euclase (BeAlSiOo(OH)),and phenakite (BerSiOo)have been quantitatively evaluatedfrom a com- bination of new phase-equilibrium, solubility, calorimetric, and volumetric measurements and with data from the literature. The resulting thermodynamic model is consistentwith natural low-variance assemblagesand can be used to interpret many beryllium-mineral occurTences. Reversedhigh-pressure solid-media experimentslocated the positions of four reactions: BerAlrSiuO,,: BeAlrOo * BerSiOo+ 5SiO, (dry) 20BeAlSiOo(OH): 3BerAlrsi6or8+ TBeAlrOo+ 2BerSiOn+ l0HrO 4BeAlSiOo(OH)+ 2SiOr: BerAlrSiuO,,+ BeAlrOo+ 2H2O BerAlrSiuO,,+ 2AlrSiOs : 3BeAlrOa + 8SiO, (water saturated). Aqueous silica concentrationswere determined by reversedexperiments at I kbar for the following sevenreactions: 2BeO + H4SiO4: BerSiOo+ 2H2O 4BeO + 2HoSiOo: BeoSirO'(OH),+ 3HrO BeAlrOo* BerSiOo+ 5H4Sio4: Be3AlrSiuOr8+ loHro 3BeAlrOo+ 8H4SiO4: BerAlrSiuOrs+ 2AlrSiO5+ l6HrO 3BerSiOo+ 2AlrSiO5+ 7H4SiO4: 2BerAlrSiuOr8+ l4H2o aBeAlsioloH) + Bersio4 + 7H4sio4:2BerAlrsiuors + 14Hro 2BeAlrOo+ BerSiOo+ 3H4SiOo: 4BeAlSiOr(OH)+ 4HrO. -

Pyrophyllite Solid Solutions in the System A|,O,-S|O,-H,O
American Minerulogist, Volume 59, pages 254-260, 1974 PyrophylliteSolid Solutions in the SystemA|,O,-S|O,-H,O Pnrr,rp E. RoseNnenc D ep art ment ol G eolo gy, 14as hing ton Stat e U nio er sity, P ullman, 14as hington 99 I 6 3 Abstract Pyrophyllite solid solutions have been synthesized in the system Al,O'-SiOr-H,O between 400' and 565'C at 2 kbar from a variety of starting materials using sealed gold tubes and conventional hydrothermal techniques. The duration of experiments was 3-9 weeks. Products were characterized by X-ray measurementsand by infrared spectroscopy. Appreciably larger basal spacings were observed for pyrophyllite synthesized from gels than for natural pyrophyllite; small amounts of quartz were present in these samples. Basal spacings of pyrophyllite synthesized from mixtures of kaolinite and quartz approach but do not equal those of natural pyrophyllite. Rehydroxylation of dehydroxylated pyrophyllite under hydrothermal conditions suggests that enlargement of basal spacings cannot be due to dehydroxylation. Substitution of the type Al"* + H* : Sia* is proposed to explain the observed variations. The coupled substitution of Al3* and (OH)- for Sin*and O- results in expanded basal spacingsdue largely to the formation of OH on the basal surface and in increased thermal stability due to the formation of H-bonds between oxygens in adjacent silica sheets.Analyses of natural pyrophyllite also suggest limited substitution of this type. Failure to recognize these substitutions in synthetic samples accounts, in part, for dis- crepancies in the reported thermal stability of pyrophyllite. Phase characterization, often lack- ing, is essentialin experimentalstudies of mineral stabilities. -

The Pyrophyllite Deposits of North Carolina
North Carolina Department of Conservation and Development Wade H. Phillips, Director BULLETIN NUMBER 37 THE PYROPHYLLITE DEPOSITS OF NORTH CAROLINA With A MORE DETAILED ACCOUNT OF THE GEOLOGY OF THE DEEP RIVER REGION By JASPER L. STUCKEY, Ph. D. RALEIGH 19 28 MEMBERS OF THE BOARD OF CONSERVATION AND DEVELOPMENT Governor A. W. McLean, Chairman, ex offtcio Raleigh S. Wade Marr __._ Raleigh B. B. Gossett Charlotte Jas. G. K. McClure, Jr Asheville Fred I. Sutton ~ _: .. Kinston E. D. Cranford . Asheboro R. Bruce Btheridge Manteo Santford Martin . ; Winston-Salem E. S. Askew Merry Hill J. Q. Gilket Marion F. S. Worthy Washington George L. Hampton Canton Frank H. Stedman Fayetteville Wade H. Phillips, Director, Raleigh LETTER OF TRANSMITTAL Raleigh, N. C, August 1, 1928. To His Excellency, Hon. A. W. McLean, Governor of North Carolina. Sir:—I herewith submit for publication as Bulletin No. 37 of the publications of the North Carolina Department of Con servation and Development a report on The Pyrophyllite De posits of North Carolina, which has been prepared by Dr. Jasper L. Stuckey, former State Geologist. This is the first complete report on the pyrophyllite deposits of this State and will, therefore, be of great interest to those who desire infor mation on such material. Yours respectfully, Wade H. Phillips, Director, North Carolina Department of Conservation and Development. AUTHOR'S FOREWORD This report was begun as a special investigation of the geology and pyrophyllite deposits of the Deep River Region, and accord ingly a detailed geologic map of that region was prepared. As the work progressed, other pyrophyllite deposits were found outside the area mapped. -

Minerals Found in Michigan Listed by County
Michigan Minerals Listed by Mineral Name Based on MI DEQ GSD Bulletin 6 “Mineralogy of Michigan” Actinolite, Dickinson, Gogebic, Gratiot, and Anthonyite, Houghton County Marquette counties Anthophyllite, Dickinson, and Marquette counties Aegirinaugite, Marquette County Antigorite, Dickinson, and Marquette counties Aegirine, Marquette County Apatite, Baraga, Dickinson, Houghton, Iron, Albite, Dickinson, Gratiot, Houghton, Keweenaw, Kalkaska, Keweenaw, Marquette, and Monroe and Marquette counties counties Algodonite, Baraga, Houghton, Keweenaw, and Aphrosiderite, Gogebic, Iron, and Marquette Ontonagon counties counties Allanite, Gogebic, Iron, and Marquette counties Apophyllite, Houghton, and Keweenaw counties Almandite, Dickinson, Keweenaw, and Marquette Aragonite, Gogebic, Iron, Jackson, Marquette, and counties Monroe counties Alunite, Iron County Arsenopyrite, Marquette, and Menominee counties Analcite, Houghton, Keweenaw, and Ontonagon counties Atacamite, Houghton, Keweenaw, and Ontonagon counties Anatase, Gratiot, Houghton, Keweenaw, Marquette, and Ontonagon counties Augite, Dickinson, Genesee, Gratiot, Houghton, Iron, Keweenaw, Marquette, and Ontonagon counties Andalusite, Iron, and Marquette counties Awarurite, Marquette County Andesine, Keweenaw County Axinite, Gogebic, and Marquette counties Andradite, Dickinson County Azurite, Dickinson, Keweenaw, Marquette, and Anglesite, Marquette County Ontonagon counties Anhydrite, Bay, Berrien, Gratiot, Houghton, Babingtonite, Keweenaw County Isabella, Kalamazoo, Kent, Keweenaw, Macomb, Manistee, -
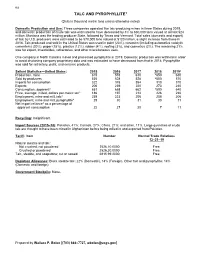
Talc Data Sheet
162 TALC AND PYROPHYLLITE1 (Data in thousand metric tons unless otherwise noted) Domestic Production and Use: Three companies operated five talc-producing mines in three States during 2019, and domestic production of crude talc was estimated to have decreased by 3% to 630,000 tons valued at almost $24 million. Montana was the leading producer State, followed by Texas and Vermont. Total sales (domestic and export) of talc by U.S. producers were estimated to be 570,000 tons valued at $120 million, a slight increase from those in 2018. Talc produced and sold in the United States was used in paint (23%), ceramics (including automotive catalytic converters) (20%), paper (15%), plastics (12%), rubber (4%), roofing (3%), and cosmetics (2%). The remaining 21% was for export, insecticides, refractories, and other miscellaneous uses. One company in North Carolina mined and processed pyrophyllite in 2019. Domestic production was withheld in order to avoid disclosing company proprietary data and was estimated to have decreased from that in 2018. Pyrophyllite was sold for refractory, paint, and ceramic products. Salient Statistics—United States: 2015 2016 2017 2018 2019e Production, mine 615 578 610 e650 630 Sold by producers 535 528 528 e550 570 Imports for consumption 322 378 354 313 310 Exports 206 239 220 273 240 Consumption, apparent2 651 668 662 e590 640 Price, average, milled, dollars per metric ton3 186 197 214 226 230 Employment, mine and mill, talc4 239 223 206 208 206 Employment, mine and mill, pyrophyllite4 29 30 31 30 31 Net import reliance5 as a percentage of apparent consumption 22 27 20 7 11 Recycling: Insignificant. -

Clay Minerals
CLAY MINERALS CD. Barton United States Department of Agriculture Forest Service, Aiken, South Carolina, U.S.A. A.D. Karathanasis University of Kentucky, Lexington, Kentucky, U.S.A. INTRODUCTION of soil minerals is understandable. Notwithstanding, the prevalence of silicon and oxygen in the phyllosilicate structure is logical. The SiC>4 tetrahedron is the foundation Clay minerals refers to a group of hydrous aluminosili- 2 of all silicate structures. It consists of four O ~~ ions at the cates that predominate the clay-sized (<2 |xm) fraction of apices of a regular tetrahedron coordinated to one Si4+ at soils. These minerals are similar in chemical and structural the center (Fig. 1). An interlocking array of these composition to the primary minerals that originate from tetrahedral connected at three corners in the same plane the Earth's crust; however, transformations in the by shared oxygen anions forms a hexagonal network geometric arrangement of atoms and ions within their called the tetrahedral sheet (2). When external ions bond to structures occur due to weathering. Primary minerals form the tetrahedral sheet they are coordinated to one hydroxyl at elevated temperatures and pressures, and are usually and two oxygen anion groups. An aluminum, magnesium, derived from igneous or metamorphic rocks. Inside the or iron ion typically serves as the coordinating cation and Earth these minerals are relatively stable, but transform- is surrounded by six oxygen atoms or hydroxyl groups ations may occur once exposed to the ambient conditions resulting in an eight-sided building block termed an of the Earth's surface. Although some of the most resistant octohedron (Fig. -

Phyllosilicates – (Silicate Sheets)
Phyllosilicates – (Silicate Sheets) 2- Many members have a platy (Si2O5) or flaky habit with one very Tetrahedral sheet (6-fold) prominent cleavage . Minerals are generally soft, low specific gravity, may even be flexible. Most are hydroxyl bearing. Each tetrahedra is bound to three neiggghboring tetrahedra via three basal bridging oxygens. The apical oxygen of each tetrahedral in a sheet all point in the same direction. The sheets are stacked either apice-to- apice or base-to-base. In an undistorted sheet the hydroxyl (OH) group sits in the centre and each outlined triangle is equivalent. Sheets within sheets…. Apical oxygens, plus the –OH group, coordinate a 6-fold (octahedral) site (XO6). These octahedral sites form infinitely extending sheets. All the octahedra lie on triangular faces, oblique to the tetrahedral sheets. The most common elements found in the 6 -fold site are Mg (or Fe) or Al . Dioctahedral vs Trioctahedral Mg and Al have different charges, but the sheet must remain charge neutral . With 6 coordinating oxygens, we have a partial charge of -6. How many Mg2+ ions are required to retain neutrality? How many Al3+ ions are required to retain neutrality? Mg occupies all octahedral sites, while Al will only occupy 2 out of every 3. The stacking of the sheets dictates the crystallography and c hem istry o f eac h o f t he p hhyll llosili cates. Trioctahedral Dioctahedral O Brucite Gibbsite Hydroxyl Magnesium Aluminium Trioctahedral Is this structure charge neutral? T O T Interlayer Cation T O T Potassium (K+) Phlogopite (Mg end-member biotite) Dioctahedral Is this structure charge neutral? T O T Interlayer Cation T O T Potassium (K+) Muscovite Compositional variation in phyllosilicates There is little solid solution between members of the dioctahedral and trioctahedral groups. -

X-Ray Determination of Superstructure Of
Clay Science 10, 15-35 (1996) X-RAY DETERMINATION OF SUPERSTRUCTURE OF PYROPHYLLITE FROM YANO-SHOKOZAN MINE, HIROSHIMA, JAPAN ANDRZEJ WIEWIORA1 AND TADATAKA HIDA2 Institute of Geological Sciences, Polish Academy of Sciences, 02-089 1 Warsaw, Al. Zwirki i Wigury 93, Poland 2 Shokozan Research Laboratory Co . Ltd., Nishihon-machi, Shobara-shi, Hiroshima, 727 Japan (Accepted August 28, 1996) ABSTRACT Observation of the pyrophyllites from Nakamuraguchi and Takinotani under SEM showed typical particles morphology and sizes in the range of 0.1-1ƒÊm in thickness and several ƒÊm in diameter. Chemical analyses conducted with the use of WDS spectrometers proved classical pyrophyllite composition, with minor admixture of Fe. By IR method location of Fe3+ in octahedra has been confirmed. Based on the diffraction patterns it was demonstrated that pyrophyllite from Nakamuraguchi mainly consists of the monoclinic form whereas pyrophyllite from Takinotani consists of mixture up to 20% of the triclinic form. X-ray diffraction patterns from powdered samples, displayed sharp basal and subfamily reflections and strongly blurred polytypic reflections indicating a significant structural disorder. Transmission diffraction patterns from non-powdered needle- like aggregate displayed in addition the basal reflections of a series d00l•El=18.4A. They are due to the superstructure where d001 spacing is double of the spacing of pyrophyllite. Simulated pattern for the superstructure displayed d00l•El=18.4A series of basal reflections also a reflection 111 at 4.16A of similar intensity to the one in experimental pattern. A mixture of 70% superstructure, 25% of monoclinic and 5% of triclinic structure gives the best match to the experimental diffractogram of pyrophyllite from Nakamuraguchi and Takinotani. -

Figure 1: Location of Principal Shallow Conductors at Alpala (Anomalies C0
Figure 1: Location of principal shallow conductors at Alpala (anomalies C0-C10; 5 Ohm/m surfaces, red) and shallow zones of electrical chargeability (85 mSecs, yellow-green) shown on iso-surfaces of MVI magnetics (blue). The main concentration of shallow conductive anomalies (caused by sulphides, fracturing and clays) and chargeable rocks (caused by disseminated sulphide and/or clays) occurs under the Northwest Alpala lithocap. Conductive bodies form more discreet responses than the chargeable responses and tightly constrain areas of interest that lie in magnetic rocks beneath these stronger conductive responses. The enveloping chargeability anomalies (yellow-green) are typical of the ‘pyrite shell’ that forms around porphyry systems. Figure 2: A northwest-trending belt of deep magnetic anomalies (brown) are overlain by chargeability anomalies which are concentrated above the northwest lithocap, consistent with an extensive pyrite shell within the lithocap above and around the Northwest Alpala porphyry target (T1). Figure 3: Image looking northeast, showing an MVI model iso-surface (0.0054 SI units; turquoise surface) defining the Central Alpala and Northwest Alpala MVI anomaly, the location of drill holes 1-9 and two horizontal slices through the Alpala Orion Deep Conductivity model. The rocks within and surrounding the magnetic anomaly at Central and Northwest Alpala are conductive, caused by the likely presence of sulphides and fracturing (veining) associated with magnetic rocks that contain hydrothermal magnetite associated with potassic alteration. Importantly Hole 5 (532 m @ 1.05% Cu and 1.08 g/t Au) tested the southeast margin of the highly prospective T1 target. Figure 4: Location of the high priority target T1 at Alpala beneath the northwest lobe of the surface alteration lithocap (white outline), while the dashed white outlines show areas of potential target extension beyond the core target area. -

Clay Minerals in Hydrothermal Systems
minerals Review Clay Minerals in Hydrothermal Systems Paolo Fulignati Dipartimento di Scienze della Terra, University of Pisa, Via S. Maria 53, 56126 Pisa, Italy; [email protected] Received: 24 August 2020; Accepted: 14 October 2020; Published: 16 October 2020 Abstract: The study of active and fossil hydrothermal systems shows clay minerals to be a fundamental tool for the identification and characterization of hydrothermal alteration facies. The occurrence and composition of hydrothermal alteration facies could provide useful information on the physicochemical conditions of the hydrothermal activity affecting a rock volume. In particular, clay minerals (i.e., smectite group, chlorite, illite, kaoline group, pyrophyllite, biotite) are pivotal for extrapolating important parameters that strongly affect the development of water/rock interaction processes such as the temperature and pH of the hydrothermal environment. This work aims to give a general reference scheme concerning the occurrence of clay minerals in hydrothermal alteration paragenesis, their significance, and the information that can be deduced by their presence and chemical composition, with some examples from active and fossil hydrothermal systems around the world. The main mineralogical geothermometers based on chlorite and illite composition are presented, together with the use of hydrogen and oxygen isotope investigation of clay minerals in hydrothermal systems. These techniques provide a useful tool for the reconstruction of the origin and evolution of fluids involved in hydrothermal alteration. Finally, a list of oxygen and hydrogen fractionation factor equations between the main clay minerals and water is also provided. Keywords: clay minerals; hydrothermal alteration; hydrothermal mineralogical paragenesis; geothermometers 1. Introduction A volume of rock, when affected by hydrothermal fluid circulation, typically undergoes a variety of alteration processes. -

Applications to Exploration in Other Areas
Mineralogy variations in the Mamadawerre Sandstone, Kombolgie Subgroup at Angularli Uranium Prospect: applications to exploration in other areas. Belinda Smith NTGS Mamadawerre Sandstone – visual logging WRD0085 WRDD0136 “strongly “strongly weathered, highly bleached… fractured…” “patchy fracture diagenetic hematite” coated with “fractured zone has clay- white clay” filled gouges… leached” Which hole overlies mineralisation?? Angularli prospect – geology and uranium Inferred Resource 0.91Mt @ 1.3% U3O8 (~26Mlbs U3O8) Vimy Resources ASX announcement 20 March 2018 Modified from Hollis and Glass, 2012. Howship and Oenpelli 1:100,000 Explanatory Notes p6 Oenpelli Dolerite to north Angularli Prospect WRD0117 Mamadawerre Sandstone at surface Angularli fault zone WRDD0134 long section Bathurst Island Formation (cover) Oenpelli Dolerite WRD0117 Angularli fault zone WRDD0134 (distal to mineralisation drillhole) unconformity surface (unscanned) ore zone Mineralisation in hangingwall of structural zone Angularli Prospect (King, 2012) Silica-sericite-clay-pyrite alteration (basement) Sandstone mineralogy not described WRD0117 Oenpelli Dolerite WRDD0134 WRD0105 unconformity surface (unscanned) ore zone above and below unconformity Angularli fault zone ‘silica flooded breccia’ (SFB) “Primary uranium mineralisation has developed in the hangingwall of the Angularli fault, within the SFB and the overlying sandstone.” Vimy Resources ASX Announcement 20 March 2018 Measuring mineralogy variations HYMAP Reflectance spectroscopy: measuring ASTER absorption -

F^ the Journal of \ Y Volume 26 No
Gemmologf^ The Journal of \ y Volume 26 No. 6 April 1999 II J The Gemmological Association and Gem Testing Laboratory of Great Britain Gemmological Association and Gem Testing Laboratory of Great Britain 27 Greville Street, London EC1N 8TN Tel: 0171 404 3334 Fax: 0171 404 8843 e-mail: [email protected] Website: www.gagtl.ac.uk/gagtl President: Professor R.A. Howie Vice-Presidents: E.M. Bruton, A.E. Farn, D.G. Kent, R.K. Mitchell Honorary Fellows: R.A. Howie, R.T. Liddicoat Jnr, K. Nassau Honorary Life Members: D.J. Callaghan, E.A. Jobbins, H. Tillander Council of Management: T.J. Davidson, N.W. Deeks, R.R. Harding, MJ. O'Donoghue, I. Thomson, V.R Watson Members' Council: A.J. Allnutt, P. Dwyer-Hickey, S.A. Everitt, A.G. Good, J. Greatwood, B. Jackson, J. Kessler, J. Monnickendam, L. Music, J.B. Nelson, P.G. Read, R. Shepherd, P.J. Wates, C.H. Winter Branch Chairmen: Midlands - G.M. Green, North West - L Knight, Scottish - B. Jackson Examiners: A.J. Allnutt, M.Sc, Ph.D., FGA, L. Bartlett, B.Sc, M.Phil., FGA, DGA, E.M. Bruton, FGA, DGA, S. Coelho, B.Sc, FGA, DGA, Prof. A.T. Collins, B.Sc, Ph.D, A.G. Good, FGA, DGA, J. Greatwood, FGA, G.M. Howe, FGA, DGA, G.H. Jones, B.Sc, Ph.D., FGA, M. Newton, B.Sc, D.Phil, C.J.E. Oldershaw, B.Sc (Hons), FGA, H.L. Plumb, B.Sc, FGA, DGA, R.D. ROSS, B.Sc, FGA, DGA, PA. Sadler, B.Sc, FGA, DGA, E.