Interferometry & Asteroseismology of Delta Scu} Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Divinus Lux Observatory Bulletin: Report #28 100 Dave Arnold
Vol. 9 No. 2 April 1, 2013 Journal of Double Star Observations Page Journal of Double Star Observations VOLUME 9 NUMBER 2 April 1, 2013 Inside this issue: Using VizieR/Aladin to Measure Neglected Double Stars 75 Richard Harshaw BN Orionis (TYC 126-0781-1) Duplicity Discovery from an Asteroidal Occultation by (57) Mnemosyne 88 Tony George, Brad Timerson, John Brooks, Steve Conard, Joan Bixby Dunham, David W. Dunham, Robert Jones, Thomas R. Lipka, Wayne Thomas, Wayne H. Warren Jr., Rick Wasson, Jan Wisniewski Study of a New CPM Pair 2Mass 14515781-1619034 96 Israel Tejera Falcón Divinus Lux Observatory Bulletin: Report #28 100 Dave Arnold HJ 4217 - Now a Known Unknown 107 Graeme L. White and Roderick Letchford Double Star Measures Using the Video Drift Method - III 113 Richard L. Nugent, Ernest W. Iverson A New Common Proper Motion Double Star in Corvus 122 Abdul Ahad High Speed Astrometry of STF 2848 With a Luminera Camera and REDUC Software 124 Russell M. Genet TYC 6223-00442-1 Duplicity Discovery from Occultation by (52) Europa 130 Breno Loureiro Giacchini, Brad Timerson, Tony George, Scott Degenhardt, Dave Herald Visual and Photometric Measurements of a Selected Set of Double Stars 135 Nathan Johnson, Jake Shellenberger, Elise Sparks, Douglas Walker A Pixel Correlation Technique for Smaller Telescopes to Measure Doubles 142 E. O. Wiley Double Stars at the IAU GA 2012 153 Brian D. Mason Report on the Maui International Double Star Conference 158 Russell M. Genet International Association of Double Star Observers (IADSO) 170 Vol. 9 No. 2 April 1, 2013 Journal of Double Star Observations Page 75 Using VizieR/Aladin to Measure Neglected Double Stars Richard Harshaw Cave Creek, Arizona [email protected] Abstract: The VizierR service of the Centres de Donnes Astronomiques de Strasbourg (France) offers amateur astronomers a treasure trove of resources, including access to the most current version of the Washington Double Star Catalog (WDS) and links to tens of thousands of digitized sky survey plates via the Aladin Java applet. -

Binocular Double Star Logbook
Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club. -

Gaia Data Release 2 Special Issue
A&A 623, A110 (2019) Astronomy https://doi.org/10.1051/0004-6361/201833304 & © ESO 2019 Astrophysics Gaia Data Release 2 Special issue Gaia Data Release 2 Variable stars in the colour-absolute magnitude diagram?,?? Gaia Collaboration, L. Eyer1, L. Rimoldini2, M. Audard1, R. I. Anderson3,1, K. Nienartowicz2, F. Glass1, O. Marchal4, M. Grenon1, N. Mowlavi1, B. Holl1, G. Clementini5, C. Aerts6,7, T. Mazeh8, D. W. Evans9, L. Szabados10, A. G. A. Brown11, A. Vallenari12, T. Prusti13, J. H. J. de Bruijne13, C. Babusiaux4,14, C. A. L. Bailer-Jones15, M. Biermann16, F. Jansen17, C. Jordi18, S. A. Klioner19, U. Lammers20, L. Lindegren21, X. Luri18, F. Mignard22, C. Panem23, D. Pourbaix24,25, S. Randich26, P. Sartoretti4, H. I. Siddiqui27, C. Soubiran28, F. van Leeuwen9, N. A. Walton9, F. Arenou4, U. Bastian16, M. Cropper29, R. Drimmel30, D. Katz4, M. G. Lattanzi30, J. Bakker20, C. Cacciari5, J. Castañeda18, L. Chaoul23, N. Cheek31, F. De Angeli9, C. Fabricius18, R. Guerra20, E. Masana18, R. Messineo32, P. Panuzzo4, J. Portell18, M. Riello9, G. M. Seabroke29, P. Tanga22, F. Thévenin22, G. Gracia-Abril33,16, G. Comoretto27, M. Garcia-Reinaldos20, D. Teyssier27, M. Altmann16,34, R. Andrae15, I. Bellas-Velidis35, K. Benson29, J. Berthier36, R. Blomme37, P. Burgess9, G. Busso9, B. Carry22,36, A. Cellino30, M. Clotet18, O. Creevey22, M. Davidson38, J. De Ridder6, L. Delchambre39, A. Dell’Oro26, C. Ducourant28, J. Fernández-Hernández40, M. Fouesneau15, Y. Frémat37, L. Galluccio22, M. García-Torres41, J. González-Núñez31,42, J. J. González-Vidal18, E. Gosset39,25, L. P. Guy2,43, J.-L. Halbwachs44, N. C. Hambly38, D. -
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical
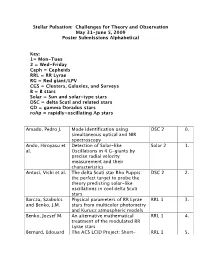
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical Key: 1= Mon-Tues 2 = Wed-Friday Ceph = Cepheids RRL = RR Lyrae RG = Red giant/LPV CGS = Clusters, Galaxies, and Surveys B = B stars Solar = Sun and solar-type stars DSC = delta Scuti and related stars GD = gamma Doradus stars roAp = rapidly-oscillating Ap stars Amado, Pedro J. Mode identification using DSC 2 0. simultaneous optical and NIR spectroscopy Ando, Hiroyasu et Detection of Solar-like Solar 2 1. al. Oscillations in 4 G-giants by precise radial velocity measurement and their characteristics Antoci, Vichi et al. The delta Scuti star Rho Puppis: DSC 2 2. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Barcza, Szabolcs Physical parameters of RR Lyrae RRL 1 3. and Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical RRL 1 4. treatment of the modulated RR Lyrae stars Bernard, Edouard The ACS LCID Project: Short- RRL 1 5. for the LCID Team period variables Bersier, David et A large-scale survey for variable CGS 1 6. al. stars in M33 Bouabid, Mehdi- Frequency analysis of the SISMO GD 2 7. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid GD 2 8. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Cameron, Chris et Asteroseismic tuning of the roAp 2 9. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the B 2 10. al. MOST asteroseismic potential Cameron, Chris, Frequency Analysis of the Beta B 2 11. -
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical
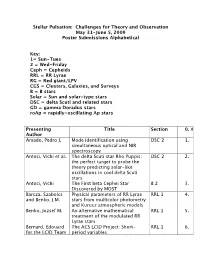
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Alphabetical Key: 1= Sun-Tues 2 = Wed-Friday Ceph = Cepheids RRL = RR Lyrae RG = Red giant/LPV CGS = Clusters, Galaxies, and Surveys B = B stars Solar = Sun and solar-type stars DSC = delta Scuti and related stars GD = gamma Doradus stars roAp = rapidly-oscillating Ap stars Presenting Title Section 0. # Author Amado, Pedro J. Mode identification using DSC 2 1. simultaneous optical and NIR spectroscopy Antoci, Vichi et al. The delta Scuti star Rho Puppis: DSC 2 2. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Antoci, Vichi The First beta Cephei Star B 2 3. Discovered by MOST Barcza, Szabolcs Physical parameters of RR Lyrae RRL 1 4. and Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical RRL 1 5. treatment of the modulated RR Lyrae stars Bernard, Edouard The ACS LCID Project: Short- RRL 1 6. for the LCID Team period variables Bersier, David et A large-scale survey for variable CGS 1 7. al. stars in M33 Bouabid, Mehdi- Frequency analysis of the SISMO GD 2 8. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid GD 2 9. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Breger, M., Lenz, Is 44 Tau in the post-MS DS 2 10. Patrick, and contraction phase? Pamyatnykh, A. Cameron, Chris et Asteroseismic tuning of the roAp 2 11. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the B 2 12. -

Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions
Stellar Pulsation: Challenges for Theory and Observation May 31-June 5, 2009 Poster Submissions Presenting Author Title 0. # Amado, Pedro J. Mode identification using 1. simultaneous optical and NIR spectroscopy Ando, Hiroyasu et Detection of Solar-like Oscillations 2. al. in 4 G-giants by precise radial velocity measurement and their characteristics Antoci, Vichi et al. The delta Scuti star Rho Puppis: 3. the perfect target to probe the theory predicting solar-like oscillations in cool delta Scuti stars Barcza, Szabolcs and Physical parameters of RR Lyrae 4. Benko, J.M. stars from multicolor photometry and Kurucz atmospheric models Benko, Jozsef M. An alternative mathematical 5. treatment of the modulated RR Lyrae stars Bernard, Edouard for The ACS LCID Project: Short- 6. the LCID Team period variables Bouabid, Mehdi- Frequency analysis of the SISMO 7. Pierre $\gamma$Doradus star HD 49434 Bouabid, Mehdi- Hybrid 8. Pierre $\gamma$Doradus/$\delta$Scuti stars: theory versus observations Cameron, Chris et Asteroseismic tuning of the 9. al. magnetic field of the roAp star HR 1217 Cameron, Chris et Near-critical rotation offers the 10. al. MOST asteroseismic potential Cash, Jennifer et al. A Long Term Photometric and 11. Spectroscopic Study of RV Tauri stars Chadid, Merieme et First light curves from Antarctica: 12. al. PAIX monitoring of the Blazhko stars Chavez, Joy M. et al. A Cepheid Distance to the 13. Antennae De Cat, Peter et al. Is HD147787 a double-lined 14. binary with two pulsating components? De Cat, Peter et al. Towards asteroseismology of 15. main-sequence g-mode pulsators: spectroscopic multi- site campaigns for slowly pulsating B stars and gamma Doradus stars. -

A5230e006841b78f672998e630
The Astrophysical Journal, 697:522–534, 2009 May 20 doi:10.1088/0004-637X/697/1/522 C 2009. The American Astronomical Society. All rights reserved. Printed in the U.S.A. ASTEROSEISMOLOGICAL MODELING OF THE MULTIPERIODIC λ BOOTIS STAR 29 CYGNI R. Casas, A. Moya, J. C. Suarez´ 1,S.Mart´ın-Ru´ız, P. J. Amado, C. Rodr´ıguez-Lopez´ 2, and R. Garrido Instituto de Astrof´ısica de Andaluc´ıa (CSIC), Granada, Spain, CP3004 Received 2008 September 3; accepted 2009 February 26; published 2009 May 4 ABSTRACT The present work focuses on the discussion of the λ Bootis nature of the multiperiodic δ Scuti star HD 192640 (29 Cyg), through a comprehensive asteroseismic modeling. Some of the most recent asteroseismic tools are used to check whether the observed low metallicity is internal, i.e., intrinsic, present throughout the star, or due to superficial processes as accretion, diffusive settling, radiative levitation, mass loss, etc. The modeling method uses some of the most recent tools, including: (1) effects of rotation on equilibrium models, on the adiabatic oscillation spectrum, and its influence in multicolor observables, (2) nonadiabatic stability of radial and nonradial modes, (3) inclusion of the atmosphere–pulsation interaction for a more accurate multicolor mode identification, and (4) ratio between radial modes n = 4 and n = 5 in the framework of Petersen diagrams. The analysis performed reveals that the models fulfilling all the constraints are those in the middle of the main sequence (MS), with subsolar metallicity, except some other unlikely possibilities. Therefore, this study does not support the idea of the λ Bootis stars being zero-age MS or pre-MS stars interacting with their primordial cloud of gas and dust, but suggest the explanation of their nature as submetallic MS objects. -

Information Bulletin on Variable Stars
COMMISSIONS AND OF THE I A U INFORMATION BULLETIN ON VARIABLE STARS Nos March November EDITORS L SZABADOS K OLAH TECHNICAL EDITOR A HOLL TYPESETTING K ORI ADMINISTRATION Zs KOVARI EDITORIAL BOARD L A BALONA M BREGER E BUDDING M deGROOT E GUINAN D S HALL P HARMANEC M JERZYKIEWICZ K C LEUNG M RODONO N N SAMUS J SMAK C STERKEN H BUDAPEST XI I Box HUNGARY HU ISSN COPYRIGHT NOTICE IBVS is published on b ehalf of the th and nd Commissions of the IAU by the Konkoly Observatory Budap est Hungary Individual issues could b e downloaded for scientic and educational purp oses free of charge Bibliographic information of the recent issues could b e entered to indexing sys tems No IBVS issues may b e stored in a public retrieval system in any form or by any means electronic or otherwise without the prior written p ermission of the publishers Prior written p ermission of the publishers is required for entering IBVS issues to an electronic indexing or bibliographic system to o CONTENTS E PAUNZEN G HANDLER Pulsation of HD and HD :::: E PAUNZEN WW WEISS R KUSCHNIG Nonvariability among Bo o Star I ESO and Data :::::::::::::::::::::::::::::::::: PA HECKERT Photometry of SV Camelopardalis :::::::::::::::: M WOLF L SAROUNOVA P MOLIK Period Changes in V Ophiuchi ::::::::::::::::::::::::::::::::::::::::::::::::::: ::::::::::::: RM ROBB MD GLADDERS Optical Observations of the Active Star FF Cancri ::::::::::::::::::::::::::::::::::::::::::::::::::: ::::::: U BASTIAN E BORN F AGERER M DAHM V GROSSMANN V MAKAROV Conrmation of the -

Articles Dans Des Revues À Comité De Lecture
Articles dans des revues à comité de lecture 2012 [ACL005] Barstow Joanna K., Tsang C. C. C., Wilson C. F., Irwin P. G. J., Taylor F. W., McGouldrick Kevin, Drossart [ACL001] Abramowski A., Acero F., Aharonian F., Pierre, Piccioni G., Tellmann Silvia. Models of the global cloud Akhperjanian A. G., Anton G., Balzer A., Barnacka A., Barres de structure on Venus derived from Venus Express observations. Almeida U., Becherini Y., Becker J., Behera B., Benbow W., Icarus, 2012, vol. 217, pp. 542-560. Bernlöhr K., Bochow A., Boisson C., Bolmont J., Bordas P., Bouteilier T., Brucker J., Brun F., Brun P., Bulik T., Büsching I., [ACL006] Barucci Antonella, Belskaya Irina, Fornasier Sonia, Carrigan S., Casanova S., Cerruti M., Chadwick P. M., Fulchignoni Marcello, Clark B. E., Coradini A., Capaccioni F., Charbonnier A., Chaves R. C. G., Cheesebrough A., Chounet Dotto E., Birlan Mirel, Leyrat C., Sierks H., Thomas N., Vincent L.-M., Clapson A. C., Coignet G., Cologna G., Colom Pierre, J. B. Overview of Lutetia's surface composition. Planetary and Conrad J., Coudreau N., Dalton M., Daniel M.K., Davids I. D., Space Science, 2012, vol. 66, pp. 23-30. Degrange B., Deil C., Dickinson H. J., Djannati-Ataï A., Domainko W., Drury L. O.'C., Dubois F., Dubus G., Dutson K., [ACL007] Barucci Antonella, Merlin Frédéric, Perna Davide, Dyks J., Dyrda M., Edwards P., Egberts K., Eger P., Espigat P., Alvarez-Candal A., Müller T., Mommert M., Kiss C., Fornasier Fallon L., Farnier C., Fegan S., Feinstein F., Fernandes M. V., Sonia, Santos-Sanz Pablo, Dotto E. The extra red plutino (55638) Fiasson A., Fontaine G., Förster A., Füßling M., Gallant Y. -

STERNBILD SCHWAN (Cygnus – Cyg)
STERNBILD SCHWAN (Cygnus – Cyg) Der Schwan ist ein Sommersternbild des nördlichen Himmels. Laut Sage wurde Orpheus in einen Schwan verwandelt und zusammen mit seiner Harfe (Lyra = Leier) an den Himmel versetzt. Der Schwan befindet sich in einer äußerst sternreichen Gegend innerhalb des Milchstraßenbandes. Deneb, der Hauptstern, ist der linke obere Eckpunkt im Sommerdreieck. Wir finden im Schwan entlang der Milchstraße viele Offene Sternhaufen und Galaktische Nebel wie z.B. den „Nordamerikanebel“ NGC 7000 und den berühmten Supernova-Überrest des Cyrrusnebels. Ebenfalls bekannt ist der farbige Doppelstern „Albireo“. Der Schwan kulminiert im Juli/August gegen 24.00 Uhr. Er befindet sich innerhalb der Koordinaten RE19h10m bis 22h02m und DE +28° bis +62°. Die Nachbarsternbilder sind im Norden Kepheus und Drache, im Westen Drache und Leier, im Süden Füchschen und Pegasus, und im Osten Pegasus und EiIdechse. Der Schwan ist nördlich 62° geografischer Breite zirkumpolar und südlich –29°nicht mehr vollständig sichtbar. Die Objekte 1. Das „Kreuz des Nordens“ 2. Die Doppelsterne 3. Die Veränderlichen 4. Die Deep Sky Objekte 5. Die Röntgenquelle X-1 Cygnus 1. Das „Kreuz des Nordens“ Vom nördlichen Sommerdreieckstern Deneb ausgehend sehen wir ein auffälliges Kreuz aus Sternen der 1. bis 3. Größenklasse. Sie bilden das Gerüst des Sternbildes und markieren einen mit dem Kopf voraus fliegenden Schwan. Manchmal wird diese Formation auch das „Kreuz des Nordens“ genannt. Es sind dies die Sterne Deneb (Schwanz), Sadir (Brust), Gienah und Delta (linker und rechter Flügel), Eta (Hals) sowie Albireo (Kopf). DENEB, Alpha (α) Cygni, 50 Cygni; RE 20h 41' 26“ / DE +45° 17' arab.: „Schwanz“; mv= 1,21mag; Spektrum= A2Ia; Distanz= 3229LJ; LS= 260.000fach; Mv= -8,7Mag; MS= 19fach; RS= 203fach; OT= 8525K; Rotationsdauer= 40 Tage; Rotationsgeschwindigkeit= 20km/s (jeweils am Äquator); EB= 0.005“/Jhr.; RG= -4,5km/s; Alter ca. -

En Este Número
%2/(7Ì1 '( /$ $*583$&,Ð1 $67521Ð0,&$ 9,=&$,1$ %,=.$,.2 $6752120, (/.$57($ 1998 3er TRIMESTRE AÑO II Nº 6 EN ESTE NÚMERO... UNA MASCARA DE ENFOQUE (2), CCD ASTROFOTOGRAFIA OBSERVACIONES DE LA CCD LOS CAMINOS DEL FIRMAMENTO LAS SUPERNOVAS EL CIELO ESTE TRIMESTRE NOTICIAS BREVES EFEMERIDES Y OCULTACIONES 1 GALILEO A.A.V.-B.A.E. JULIO-AGO-SEP 1998 *$/,/(2 INDICE DE ARTICULOS Número 6 del Boletín de la Pág. AGRUPACIÓN ASTRONÓMICA VIZCAINA Taller: Una máscara de enfoque(y II)........3 BIZKAIKO ASTRONOMI ELKARTEA Supernovas .............................................5 Sede: Locales del Departamento de Cultura de la Diputación Foral de Vizcaya/Bizkaiko Foru Aldundia. Astrofotografia sin seguimiento ................8 c/ Iparragirre 46, 5º dpto. 4. Bilbao Previ-Observacion: Climatologia ............10 Apertura de locales: Martes de 19:30 a 21:00 Depósito legal: BI-420-92 Observacion de meteoros en video........ 11 Correo electrónico: [email protected] Los caminos del firmamento ..................13 Página Internet: members.xoom.com/aav/index.html Este ejemplar se distribuye de forma gratuita a los socios y colabo- CCD CookBook. Modificaciones ............15 radores de la AAV-BAE. La AAV-BAE no se hace responsable del Observando el Sol .................................16 contenido de los artículos, ni de las opiniones vertidas en ellos por sus autores. Prohibida la reproducción total o parcial de cualquier Informes de observacion AAV-BAE........18 información gráfica o escrita por cualquier medio sin permiso expre- Efemerides Planetarias..........................20 so de la AAV-BAE. AAV-BAE 1998 Ocultaciones estelares...........................21 El Cielo este trimestre............................22 * BREVES * INTERNET * ASTRONOMIA * BREVES * INTERNET * ASTRONOMIA * BREVES * INTERNET * El Telescopio NOT observa el cuerpo celeste responsable de una explosión de rayos gamma y obtiene el primer espectro inmediato de estos enigmáticos objetos del Universo. -

Poster Abstracts
Poster Abstracts Is VFTS 352 a Gravitational Wave Progenitor? Michael Abdul-Masih KU Leuven, Belgium Nearly a quarter of all massive stars will merge during their lifetimes. The contact phase of massive binaries, preceding coalescence, is poorly understood due to a lack of observational constraints: only 7 O-type overcontact binaries are currently known. Stars in these systems may suffer from enhanced mixing due to rotation and tidal effects. Such enhanced mixing can induce chemically homogeneous evolution, a fundamentally different evolutionary channel where the 2 stars remain compact, preventing them from merging. Such a channel has recently been proposed as a viable way to create close and massive blackhole binaries that can explain the GW150914 gravitational wave event. However, the viability of this GW channel depends on the efficiency of the poorly-understood mixing processes. We use VLT/optical and HST/UV data of a LMC overcontact binary that shows evidence of enhanced mixing: VFTS 352 (O4.5V+O5.5V; P = 1.12d). We present new observational constraints on the physical parameters and surface abundances (He, C, N), compare them with binary evolution models, and discuss our results in the context of the future evolution of the system as a possible GW- progenitor. Luminous Blue Variables with collimated winds Claudia Agliozzo Universidad Andres Bello, Chile Interest in the role of binarity on massive star evolution has increased, creating a debate in the massive star community regarding the description of Luminous Blue Variables (LBVs). The mass- loss necessary to quickly expel their H-envelope before evolving as Wolf Rayet stars has to occur through intense line-driven stellar winds and violent eruptions.