DOCSLIB.ORG

Determination of the Identity of an Unknown Liquid Group # My Name the Date My Period Partner #1 Name Partner #2 Name

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Determination of the Identity of an Unknown Liquid Group # My Name the Date My Period Partner #1 Name Partner #2 Name Determination of the Identity of an unknown liquid Group # My Name The date My period Partner #1 name Partner #2 name Purpose: The purpose of this lab is to determine the identity of an unknown liquid by measuring its density, melting point, boiling point, and solubility in both water and alcohol, and then comparing the results to the values for known substances. Procedure: 1) Density determination Obtain a 10mL sample of the unknown liquid using a graduated cylinder Determine the mass of the 10mL sample Save the sample for further use 2) Melting point determination Set up an ice bath using a 600mL beaker Obtain a ~5mL sample of the unknown liquid in a clean dry test tube Place a thermometer in the test tube with the sample Place the test tube in the ice water bath Watch for signs of crystallization, noting the temperature of the sample when it occurs Save the sample for further use 3) Boiling point determination Set up a hot water bath using a 250mL beaker Begin heating the water in the beaker Obtain a ~10mL sample of the unknown in a clean, dry test tube Add a boiling stone to the test tube with the unknown Open the computer interface software, using a graph and digit display Place the temperature sensor in the test tube so it is in the unknown liquid Record the temperature of the sample in the test tube using the computer interface Watch for signs of boiling, noting the temperature of the unknown Dispose of the sample in the assigned waste container 4) Solubility determination Obtain two small (~1mL) samples of the unknown in two small test tubes Add an equal amount of deionized into one of the samples Add an equal amount of ethanol into the other Mix both samples thoroughly Compare the samples for solubility Dispose of the samples in the assigned waste container Observations: The unknown is a clear, colorless liquid. There is a detectable odor, but it does not lend itself to identifying the unknown. No crystallization was ever detected in the melting point determination. The unknown started as and remained a clear, colorless liquid. During the boiling point determination, bubbles started to form around the boiling chip at first, and then the entire sample began to bubble vigorously at a steady temperature. There was no observable difference in the solubility test for the unknown either with water or ethanol. Data: Density determination Mass of sample = 7.86 g Volume of sample = 10.0mL Melting point determination Lowest temperature reached for unknown in ice bath = 4.0oC. Boiling point determination Bubbles first formed at 72oC; a steady boil was reached at 78oC. Please see the graph for further details. Solubility test Upon mixing the unknown with ethanol, there are no distinct phases. Upon mixing the unknown with water, there are no distinct phases. Data Analysis: Calculations Density determination density = = = 0.786 g/mL Figure 1.1 Boiling point determination Conclusion: After careful consideration of all the test results and all the possible identities of the unknown, the experimenters determined the unknown was, in fact, ethanol. Figure 1.2 Properties of potential identities of the unknown liquid Density Freezing Boiling Solubility* Substance (g/ml) Point (oC) Point (oC) Water Ethanol Acetone 0.79 -95.0 56.4 V V t-butanol 0.79 25.5 82.8 V V Cyclohexane 0.78 6.5 80.7 I V Ethanol 0.79 -117.0 78.8 V V 2-propanol 0.79 -89.5 82.4 V V unknown 0.79 undetermined 79.0 V V V = very soluble S = slightly soluble I = insoluble The experimenters considered the density test and the boiling test the most reliable due to the procedures used and the sensitivity of the equipment involved. After carefully calculating the density of the unknown, all the potential substances with similar or identical identities were considered (figure 1.2). As the unknown sample showed no sign of crystallization at temperatures as low as 4oC, t-butanol and cyclohexane were eliminated as possible identities, as they would have both frozen at temperatures above 4oC. In addition, cyclohexane would give different solubility test results than the unknown did. Acetone would reach its boiling point at a temperature far lower than that at which the unknown boiled at, so it too was eliminated from consideration. And as 2-propanol would have to reach 82.4oC to reach a steady boil, while the unknown sample never reached 80oC (figure 1.1), it was eliminated as well. Thus, the experimenters determined the identity of the unknown must be ethanol. .
Load more

Recommended publications
  • LATENT HEAT of FUSION INTRODUCTION When a Solid Has Reached Its Melting Point, Additional Heating Melts the Solid Without a Temperature Change
    LATENT HEAT OF FUSION INTRODUCTION When a solid has reached its melting point, additional heating melts the solid without a temperature change. The temperature will remain constant at the melting point until ALL of the solid has melted. The amount of heat needed to melt the solid depends upon both the amount and type of matter that is being melted. Therefore: Q = ML Eq. 1 f where Q is the amount of heat absorbed by the solid, M is the mass of the solid that was melted and Lf is the latent heat of fusion for the type of material that was melted, which is measured in J/kg, NOTE: to fuse means to melt. In this experiment the latent heat of fusion of water will be determined by using the method of mixtures ΣQ=0, or QGained +QLost =0. Ice will be added to a calorimeter containing warm water. The heat energy lost by the water and calorimeter does two things: 1. It melts the ice; 2. It warms the water formed by the melting ice from zero to the final equilibrium temperature of the mixture. Heat gained + Heat lost = 0 Heat needed to melt ice + Heat needed to warm the melt water + Heat lost by warn water = 0 MiceLf + MiceCw (Tf - 0) + MwCw (Tf – Tw) = 0 Eq. 2. * Note: The mass of the melted water is the same as the mass of the ice. where M = mass of warm water initially in calorimeter w Mice = mass of ice and water from the melted ice Cw = specific heat of water Lf = latent heat of fusion of water Tw = initial temperature water Tf = equilibrium temperature of mixture APPARATUS: Calorimeter, thermometer, balance, ice, water OBJECTIVE: To determine the latent heat of fusion of water PROCEDURE: 1.
    [Show full text]
  • Equation of State for Benzene for Temperatures from the Melting Line up to 725 K with Pressures up to 500 Mpa†
    High Temperatures-High Pressures, Vol. 41, pp. 81–97 ©2012 Old City Publishing, Inc. Reprints available directly from the publisher Published by license under the OCP Science imprint, Photocopying permitted by license only a member of the Old City Publishing Group Equation of state for benzene for temperatures from the melting line up to 725 K with pressures up to 500 MPa† MONIKA THOL ,1,2,* ERIC W. Lemm ON 2 AND ROLAND SPAN 1 1Thermodynamics, Ruhr-University Bochum, Universitaetsstrasse 150, 44801 Bochum, Germany 2National Institute of Standards and Technology, 325 Broadway, Boulder, Colorado 80305, USA Received: December 23, 2010. Accepted: April 17, 2011. An equation of state (EOS) is presented for the thermodynamic properties of benzene that is valid from the triple point temperature (278.674 K) to 725 K with pressures up to 500 MPa. The equation is expressed in terms of the Helmholtz energy as a function of temperature and density. This for- mulation can be used for the calculation of all thermodynamic properties. Comparisons to experimental data are given to establish the accuracy of the EOS. The approximate uncertainties (k = 2) of properties calculated with the new equation are 0.1% below T = 350 K and 0.2% above T = 350 K for vapor pressure and liquid density, 1% for saturated vapor density, 0.1% for density up to T = 350 K and p = 100 MPa, 0.1 – 0.5% in density above T = 350 K, 1% for the isobaric and saturated heat capaci- ties, and 0.5% in speed of sound. Deviations in the critical region are higher for all properties except vapor pressure.
    [Show full text]
  • The Basics of Vapor-Liquid Equilibrium (Or Why the Tripoli L2 Tech Question #30 Is Wrong)
    The Basics of Vapor-Liquid Equilibrium (Or why the Tripoli L2 tech question #30 is wrong) A question on the Tripoli L2 exam has the wrong answer? Yes, it does. What is this errant question? 30.Above what temperature does pressurized nitrous oxide change to a gas? a. 97°F b. 75°F c. 37°F The correct answer is: d. all of the above. The answer that is considered correct, however, is: a. 97ºF. This is the critical temperature above which N2O is neither a gas nor a liquid; it is a supercritical fluid. To understand what this means and why the correct answer is “all of the above” you have to know a little about the behavior of liquids and gases. Most people know that water boils at 212ºF. Most people also know that when you’re, for instance, boiling an egg in the mountains, you have to boil it longer to fully cook it. The reason for this has to do with the vapor pressure of water. Every liquid wants to vaporize to some extent. The measure of this tendency is known as the vapor pressure and varies as a function of temperature. When the vapor pressure of a liquid reaches the pressure above it, it boils. Until then, it evaporates until the fraction of vapor in the mixture above it is equal to the ratio of the vapor pressure to the total pressure. At that point it is said to be in equilibrium and no further liquid will evaporate. The vapor pressure of water at 212ºF is 14.696 psi – the atmospheric pressure at sea level.
    [Show full text]
  • Single Crystal Growth of Mgb2 by Using Low Melting Point Alloy Flux
    Single Crystal Growth of Magnesium Diboride by Using Low Melting Point Alloy Flux Wei Du*, Xugang Xian, Xiangjin Zhao, Li Liu, Zhuo Wang, Rengen Xu School of Environment and Material Engineering, Yantai University, Yantai 264005, P. R. China Abstract Magnesium diboride crystals were grown with low melting alloy flux. The sample with superconductivity at 38.3 K was prepared in the zinc-magnesium flux and another sample with superconductivity at 34.11 K was prepared in the cadmium-magnesium flux. MgB4 was found in both samples, and MgB4’s magnetization curve being above zero line had not superconductivity. Magnesium diboride prepared by these two methods is all flaky and irregular shape and low quality of single crystal. However, these two metals should be the optional flux for magnesium diboride crystal growth. The study of single crystal growth is very helpful for the future applications. Keywords: Crystal morphology; Low melting point alloy flux; Magnesium diboride; Superconducting materials Corresponding author. Tel: +86-13235351100 Fax: +86-535-6706038 Email-address: [email protected] (W. Du) 1. Introduction Since the discovery of superconductivity in Magnesium diboride (MgB2) with a transition temperature (Tc) of 39K [1], a great concern has been given to this material structure, just as high-temperature copper oxide can be doped by elements to improve its superconducting temperature. Up to now, it is failure to improve Tc of doped MgB2 through C [2-3], Al [4], Li [5], Ir [6], Ag [7], Ti [8], Ti, Zr and Hf [9], and Be [10] on the contrary, the Tc is reduced or even disappeared.
    [Show full text]
  • Laboratory Equipment Reference Sheet
    Laboratory Equipment Stirring Rod: Reference Sheet: Iron Ring: Description: Glass rod. Uses: To stir combinations; To use in pouring liquids. Evaporating Dish: Description: Iron ring with a screw fastener; Several Sizes Uses: To fasten to the ring stand as a support for an apparatus Description: Porcelain dish. Buret Clamp/Test Tube Clamp: Uses: As a container for small amounts of liquids being evaporated. Glass Plate: Description: Metal clamp with a screw fastener, swivel and lock nut, adjusting screw, and a curved clamp. Uses: To hold an apparatus; May be fastened to a ring stand. Mortar and Pestle: Description: Thick glass. Uses: Many uses; Should not be heated Description: Heavy porcelain dish with a grinder. Watch Glass: Uses: To grind chemicals to a powder. Spatula: Description: Curved glass. Uses: May be used as a beaker cover; May be used in evaporating very small amounts of Description: Made of metal or porcelain. liquid. Uses: To transfer solid chemicals in weighing. Funnel: Triangular File: Description: Metal file with three cutting edges. Uses: To scratch glass or file. Rubber Connector: Description: Glass or plastic. Uses: To hold filter paper; May be used in pouring Description: Short length of tubing. Medicine Dropper: Uses: To connect parts of an apparatus. Pinch Clamp: Description: Glass tip with a rubber bulb. Uses: To transfer small amounts of liquid. Forceps: Description: Metal clamp with finger grips. Uses: To clamp a rubber connector. Test Tube Rack: Description: Metal Uses: To pick up or hold small objects. Beaker: Description: Rack; May be wood, metal, or plastic. Uses: To hold test tubes in an upright position.
    [Show full text]
  • Liquid-Vapor Equilibrium in a Binary System
    Liquid-Vapor Equilibria in Binary Systems1 Purpose The purpose of this experiment is to study a binary liquid-vapor equilibrium of chloroform and acetone. Measurements of liquid and vapor compositions will be made by refractometry. The data will be treated according to equilibrium thermodynamic considerations, which are developed in the theory section. Theory Consider a liquid-gas equilibrium involving more than one species. By definition, an ideal solution is one in which the vapor pressure of a particular component is proportional to the mole fraction of that component in the liquid phase over the entire range of mole fractions. Note that no distinction is made between solute and solvent. The proportionality constant is the vapor pressure of the pure material. Empirically it has been found that in very dilute solutions the vapor pressure of solvent (major component) is proportional to the mole fraction X of the solvent. The proportionality constant is the vapor pressure, po, of the pure solvent. This rule is called Raoult's law: o (1) psolvent = p solvent Xsolvent for Xsolvent = 1 For a truly ideal solution, this law should apply over the entire range of compositions. However, as Xsolvent decreases, a point will generally be reached where the vapor pressure no longer follows the ideal relationship. Similarly, if we consider the solute in an ideal solution, then Eq.(1) should be valid. Experimentally, it is generally found that for dilute real solutions the following relationship is obeyed: psolute=K Xsolute for Xsolute<< 1 (2) where K is a constant but not equal to the vapor pressure of pure solute.
    [Show full text]
  • Pressure Vs Temperature (Boiling Point)
    Boiling Points and Vapor Pressure Background Boiling Points and Vapor Pressure Background: Definitions Vapor Pressure: The equilibrium pressure of a vapor above its liquid; the pressure of the vapor resulting from the evaporation of a liquid above a sample of the liquid in a closed container. Boiling Point: The temperature at which the vapor pressure of a liquid is equal to the atmospheric (or applied) pressure. As the temperature of the liquid increases, the vapor pressure will increase, as seen below: https://www.chem.purdue.edu/gchelp/liquids/vpress.html Vapor pressure is interpreted in terms of molecules of liquid converting to the gaseous phase and escaping into the empty space above the liquid. In order for the molecules to escape, the intermolecular forces (Van der Waals, dipole- dipole, and hydrogen bonding) have to be overcome, which requires energy. This energy can come in the form of heat, aka increase in temperature. Due to this relationship between vapor pressure and temperature, the boiling point of a liquid decreases as the atmospheric pressure decreases since there is more room above the liquid for molecules to escape into at lower pressure. The graph below illustrates this relationship using common solvents and some terpenes: Pressure vs Temperature (boiling point) Ethanol Heptane Isopropyl Alcohol B-myrcene 290.0 B-caryophyllene d-Limonene Linalool Pulegone 270.0 250.0 1,8-cineole (eucalyptol) a-pinene a-terpineol terpineol-4-ol 230.0 p-cymene 210.0 190.0 170.0 150.0 130.0 110.0 90.0 Temperature (˚C) Temperature 70.0 50.0 30.0 10 20 30 40 50 60 70 80 90 100 200 300 400 500 600 760 10.0 -10.0 -30.0 Pressure (torr) 1 Boiling Points and Vapor Pressure Background As a very general rule of thumb, the boiling point of many liquids will drop about 0.5˚C for a 10mmHg decrease in pressure when operating in the region of 760 mmHg (atmospheric pressure).
    [Show full text]
  • Fast Synthesis of Fe1.1Se1-Xtex Superconductors in a Self-Heating
    Fast synthesis of Fe1.1Se1-xTe x superconductors in a self-heating and furnace-free way Guang-Hua Liu1,*, Tian-Long Xia2,*, Xuan-Yi Yuan2, Jiang-Tao Li1,*, Ke-Xin Chen3, Lai-Feng Li1 1. Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, P. R. China 2.Department of Physics, Beijing Key Laboratory of Opto-electronic Functional Materials & Micro-nano Devices, Renmin University of China, Beijing 100872, P. R. China 3. State Key Laboratory of New Ceramics & Fine Processing, School of Materials Science and Engineering, Tsinghua University, Beijing 100084, P. R. China *Corresponding authors: Guang-Hua Liu, E-mail: [email protected] Tian-Long Xia, E-mail: [email protected] Jiang-Tao Li, E-mail: [email protected] Abstract A fast and furnace-free method of combustion synthesis is employed for the first time to synthesize iron-based superconductors. Using this method, Fe1.1Se1-xTe x (0≤x≤1) samples can be prepared from self-sustained reactions of element powders in only tens of seconds. The obtained Fe1.1Se1-xTe x samples show clear zero resistivity and corresponding magnetic susceptibility drop at around 10-14 K. The Fe1.1Se0.33Te 0.67 sample shows the highest onset Tc of about 14 K, and its upper critical field is estimated to be approximately 54 T. Compared with conventional solid state reaction for preparing polycrystalline FeSe samples, combustion synthesis exhibits much-reduced time and energy consumption, but offers comparable superconducting properties. It is expected that the combustion synthesis method is available for preparing plenty of iron-based superconductors, and in this direction further related work is in progress.
    [Show full text]
  • LOWERING COSTS and SIMPLIFYING WORKFLOW with the Automate 2550 SYSTEM
    HACETTEPE UNIVERSITY FACULTY OF MEDICINE HOSPITAL CENTRAL AND STAT LABORATORIES LOWERING COSTS AND SIMPLIFYING WORKFLOW WITH THE AutoMate 2550 SYSTEM Laboratory profile › 1,040-bed hospital located in Ankara, Turkey › Provides uninterrupted 24/7 inpatient, outpatient and emergency services › Employs 6 professors, 6 associate Hacettepe University Faculty of Medicine Hospital is one of the leading professors and 130 operators university hospitals in Turkey. The university is well known for its › Performs up to 6.5 million geographical location and adoption of ground breaking technologies. biochemistry and hormone While the reference site is preferred by a large number of patients, it is tests annually of particular interest to specific patient populations seeking test results › Processes up to 2 million tests from a variety of panels. With many different systems performing on instruments in more than hundreds of standard and specialized tests, the hospital’s laboratories 20 different units are driven to ensure the delivery of results without error, while › Operates a Beckman Coulter containing costs and managing workload burden. standalone AutoMate 2550 pre- For more than 16 years, the facility—which has been held up as an and post-analytical automation system in the biochemistry example of excellence in its own region, as well as all over the country— laboratory, along with a Power has been using a standalone automation system with an aliquoter Processor system with two feature. With this technology, it has enhanced patient satisfaction,
    [Show full text]
  • Freezing and Boiling Point Changes
    Freezing Point and Boiling Point Changes for Solutions and Solids Lesson Plans and Labs By Ranald Bleakley Physics and Chemistry teacher Weedsport Jnr/Snr High School RET 2 Cornell Center for Materials Research Summer 2005 Freezing Point and Boiling Point Changes for Solutions and Solids Lesson Plans and Labs Summary: Major skills taught: • Predicting changes in freezing and boiling points of water, given type and quantity of solute added. • Solving word problems for changes to boiling points and freezing points of solutions based upon data supplied. • Application of theory to real samples in lab to collect and analyze data. Students will describe the importance to industry of the depression of melting points in solids such as metals and glasses. • Students will describe and discuss the evolution of glass making through the ages and its influence on social evolution. Appropriate grade and level: The following lesson plans and labs are intended for instruction of juniors or seniors enrolled in introductory chemistry and/or physics classes. It is most appropriately taught to students who have a basic understanding of the properties of matter and of solutions. Mathematical calculations are intentionally kept to a minimum in this unit and focus is placed on concepts. The overall intent of the unit is to clarify the relationship between changes to the composition of a mixture and the subsequent changes in the eutectic properties of that mixture. Theme: The lesson plans and labs contained in this unit seek to teach and illustrate the concepts associated with the eutectic of both liquid solutions, and glasses The following people have been of great assistance: Professor Louis Hand Professor of Physics.
    [Show full text]
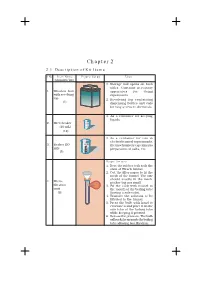
  • Chapter 2 2.1 Description of Kit Items
    Manual of SEAT Friendly MCL Kit 7 Chapter 2 2.1 Description of Kit Items S.No. Item Name Figure/Setup Uses (Quantity/ kit) 1. Storage box opens on both sides. Contains necessary 1. Wooden box apparatus for doing with revolving experiments. top 2. Revolving top containing (1) dispensing bottles and vials for easy access to chemicals. 1. As a container for keeping liquids. 2. Microbeaker (10 mL) (12) 1. As a container for use in electrochemical experiments, 3. Beaker (50 thermochemistry experiments mL) preparation of salts, etc. (3) Steps for use 1. Bore the rubber cork to fit the stem of Hirsch funnel. 2. Cut the filter paper to fit the mesh of the funnel. The size should exactly fit the mesh, 4. Micro- neither big nor small. filtration 3. Fit the cork with funnel in unit the mouth of the boiling tube (2) (having a side tube). 4. Transfer the solution to be filtrated to the funnel. 5. Press the bulb with hand to evacuate it and place it on the side tube of the boiling tube while keeping it pressed. 6. Release the pressure. The bulb will suck the air inside the boiling tube allowing fast filtration. 8 Manual of SEAT Friendly MCL Kit S.No. Item Name Figure/Setup Uses (Quantity/Kit) 1. The watch glass is used to hold solids when being 5. Watch glass weighed. (2) 2. It should never be heated. 1. Flat plate with multiple “wells” used as micro test tubes. 2. Contains 96 rectangular matrix. 3. Each well of a micro plate typically holds somewhere between a few to a few hundred microlitres of liquid.
    [Show full text]
  • Methods for the Determination of the Normal Boiling Point of a High
    Metalworking Fluids & VOC, Today and Tomorrow A Joint Symposium by SCAQMD & ILMA South Coast Air Quality Management District Diamond Bar, CA, USA March 8, 2012 Understanding & Determining the Normal Boiling Point of a High Boiling Liquid Presentation Outline • Relationship of Vapor Pressure to Temperature • Examples of VP/T Curves • Calculation of Airborne Vapor Concentration • Binary Systems • Relative Volatility as a function of Temperature • GC Data and Volatility • Everything Needs a Correlation • Conclusions Vapor Pressure Models (pure vapor over pure liquid) Correlative: • Clapeyron: Log(P) = A/T + B • Antoine: Log(P) = A/(T-C) + B • Riedel: LogP = A/T + B + Clog(T) + DTE Predictive: • ACD Group Additive Methods • Riedel: LogP = A/T + B + Clog(T) + DTE Coefficients defined, Reduced T = T/Tc • Variations: Frost-Kalkwarf-Thodos, etc. Two Parameters: Log(P) = A/T + B Vaporization as an CH OH(l) CH OH(g) activated process 3 3 G = -RTln(K) = -RTln(P) K = [CH3OH(g)]/[CH3OH(l)] G = H - TS [CH3OH(g)] = partial P ln(P) = -G/RT [CH3OH(l)] = 1 (pure liquid) ln(P) = -H/RT+ S/R K = P S/R = B ln(P) = ln(K) H/R = -A Vapor pressure Measurement: Direct versus Distillation • Direct vapor pressure measurement (e.g., isoteniscope) requires pure material while distillation based determination can employ a middle cut with a relatively high purity. Distillation allows for extrapolation and/or interpolation of data to approximate VP. • Direct vapor pressure measurement requires multiple freeze-thaw cycles to remove atmospheric gases while distillation (especially atmospheric distillation) purges atmospheric gases as part of the process. • Direct measurement OK for “volatile materials” (normal BP < 100 oC) but involved for “high boilers” (normal BP > 100 oC).
    [Show full text]