DOCSLIB.ORG

The Walman Optical Perspective on High Index Lenses

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Walman Optical Perspective on High Index Lenses Optical Perspective of Polycarbonate Material JP Wei, Ph. D. November 2011 Introduction Among the materials developed for eyeglasses, polycarbonate is one that has a number of very unique properties and provides real benefits to eyeglass wearers. Polycarbonate lenses are not only cosmetically thinner, lighter, and provide superior impact-resistance, but also produce sharp optical clarity for both central and peripheral vision. It is well-known that as the index of refraction increases dispersion also increases. In other words, the higher the refractive index, the low the ABBE value. An increase in dispersion will cause an increase in chromatic aberration. Therefore, one of the concerns in the use of lens materials such as polycarbonate is: will chromatic aberration negatively affect patient adaption? MID 1.70 LENS MATERIAL CR39 TRIVEX INDEX POLYCARBONATE 1.67 INDEX INDEX REFRACTIVE INDEX 1.499 1.529 1.558 1.586 1.661 1.700 ABBE VALUES 58 45 37 30 32 36 The refractive index of a material is often abbreviated “n.” Except for air, which has a refractive index of approximately 1, the refractive index of most substances is greater than 1 (n > 1). Water, for instance, has a refractive index of 1.333. The higher the refractive index of a lens material, the slower the light will travel through it. While it is commonly recognized that high index materials will have greater chromatic aberration than CR-39 or low refractive index lenses, there has been no quantification of the amount of visual acuity loss that results from chromatic aberration. The purpose of this paper is to review the optical properties of polycarbonate material, its advantages over other lens materials, and the impact of chromatic aberration caused by the relative low ABBE value of the material on vision and clinical significance. Refraction Index and Lens Design The refraction index of a material is simply the ratio of the speed that light passes through a vacuum to the speed that light passes through a given material. It is well known that the speed at which a ray of light will pass through a material varies with the wavelength of light. Therefore, the index of refraction of a material will vary with the wavelength of light. This necessitates that when specifying the index of refraction, the wavelength of light used is also specified. Therefore, refractive index is the measure of the bending of a ray of light when passing from one medium into another. Like polycarbonate lenses, lenses made of Trivex are thin, lightweight and more impact- resistant than regular plastic. However, polycarbonate has a higher index of refraction than Trivex (1.586 vs. 1.529), therefore polycarbonate lenses are about 10 percent thinner than Trivex lenses. The benefit for the wearer are lenses that are less conspicuous. 2 For a given lens power and the same base curve, lens material with higher refractive index will result in a flatter back curve, therefore a significantly thinner ET for minus lenses at minimal CT. For plus lenses, to achieve the same lens power with the same front base curve, higher refractive index material gives steeper back curve. With the same minimal ET, the lens will have a significantly thinner CT, especially for high plus lenses. Index of Refraction and Chromatic Dispersion Dispersion is the difference in the index of refraction at different wavelengths. The refractive index of any material also varies slightly as a function of the wavelength. Colors of light will each actually have a slightly different refractive index in the same lens material. This phenomenon is responsible for chromatic dispersion, or the breaking 3 up of white light into its component colors by prisms and lenses. Blue light, which has a higher refractive index than red light, is therefore refracted—or bent—more than red light as it passes through a lens or prism. Chromatic dispersion is a result of the fact that colors of light with shorter wavelengths, like blue, travel more slowly through most transparent materials than colors with longer wavelengths, like red. Dispersion is defined as: Relative Dispersion = (F - C) / (d - 1) . 1) In the equation 1 F is the index of refraction at the Fraunhofer F-line (486.13 nm), C is the index of refraction at the Fraunhofer C-line (656.27nm) and d is the index of refraction at the helium d-line (587.6 nm). These particular wavelengths are used because they encompass over 90% of the photopic efficiency of the human eye. The Constringence of a material is the reciprocal (inverse) of Relative Dispersion. Constringence is also called the Abbe number and is defined as: Abbe Number = d = (d - 1) / (F - C) . 2) The degree to which a given lens material will disperse light is described by a measure of its refractive efficiency or, more commonly, its Abbe value after Ernst Abbe. The following table gives the index of refraction and Abbe number for some common lens materials. Index of Refraction for Different Materials Material Refractive Index ABBE CR-39 1.498 57.8 Crown Glass 1.523 58.5 Trivex 1.529 47.0 1.56 Plastic 1.555 36.0 Polycarbonate 1.586 30.0 1.60 Plastic 1.594 37.0 1.66 Plastic 1.660 32.0 1.70 Plastic 1.70 36.0 1.70 Glass 1.701 32.0 1.80 Glass 1.805 25.4 4 Chromatic Aberration Ideally, a spectacle lens should bring all of the component colors of white light to a single point focus at the focal length of the lens. This means that the lens will refract all of the colors of white light equally, so they all intersect each other at the same location (or focus). There are two types of chromatic aberration; Longitudinal (Axial) Chromatic Aberration (LCA) and Transverse Chromatic Aberration (TCA). 1. Longitudinal Chromatic Aberration (LCA) LCA occurs when viewing on the optical axis of the lens. LCA creates multiple images along the optical axis as shown in the following figure. Longitudinal Chromatic Aberration Because the index of refraction varies with wavelength, the focal length of a lens will vary for each wavelength of light. As seen in the above figure, the blue image is focused at the shortest distance while the red image is focused at the longest distance. Longitudinal chromatic aberration is a measure of the difference in focus between the blue and red ends of the color spectrum caused by chromatic dispersion. 5 LCA can be quantified as: LCA = F / d . 3) where : F is the lens power in Diopters d is the Abbe number. From this equation, it is apparent that there is no LCA for a plano power lens and that LCA increases in direct proportion to lens power. The table below shows LCA values for some different lens powers (either plus or minus powers) and for some different lens materials. Longitudinal Chromatic Aberration (D) Versus Lens Power (D) Lens Power (D) CR-39 Trivex Poly 1.60 Index 1.70 Index 20.00 0.350 0.426 0.670 0.540 0.556 15.00 0.260 0.319 0.500 0.410 0.417 10.00 0.170 0.213 0.330 0.270 0.278 5.00 0.090 0.106 0.170 0.140 0.139 4.00 0.070 0.085 0.130 0.110 0.111 3.00 0.050 0.064 0.100 0.080 0.083 2.00 0.030 0.043 0.070 0.050 0.056 1.00 0.020 0.021 0.030 0.030 0.028 The human eye has a significant amount of LCA. Gullstrand estimated the Abbe number of the eye to be about 43 - 45. Various studies have determined the LCA of the eye to be over 2.50 D. Additionally, LCA of the eye decreases with age, particularly in the waveband of 440 - 560 nm. This is presumably due to yellowing of the crystalline lens. The graph below shows the spectral longitudinal chromatic aberration of the eye determined in the Lewis, Katz and Oehrlein study. 6 Longitudinal Chromatic Aberration of the Eye 1 0.5 0 350 400 450 500 550 600 650 700 -0.5 rs te p io -1 D -1.5 -2 -2.5 -3 Wavelength (nm) The conclusion reached is that longitudinal chromatic aberration of the lens is not significant because it is small in comparison to that of the human eye. For example, a 20.00 diopter polycarbonate lens has 0.67 D of LCA compared to 2.50 D for the eye. the visual response curve is centered on yellow and falls rapidly toward the red and blue. 2. Transverse Chromatic Aberration The second type of chromatic aberration is Transverse Chromatic Aberration (TCA). It is the off-axis equivalent of longitudinal chromatic aberration and creates multiple images displaced laterally. Transverse Chromatic Aberration 7 The following equation expresses TCA as a difference in prismatic effect: TCA = (Lens Power * Decentration) / Abbe Number . 4) TCA therefore depends only on lens power, eccentricity of gaze and the dispersion of the lens material. 3. Peripheral Vision There have been numerous studies of eye movements from the primary fixation point. Clinical studies indicated that 80% of eye movements are within 200 of the point of fixation and 100% are within 300. Beyond 300 the individual will turn their head rather than rotate their eyes. Decentration as a function of the angle of gaze is found by ray tracing various lens powers for different angles of gaze. While decentration as a function of the angle of gaze varies with lens power, in general, a decentration for a 200 gaze angle is approximately 10 mm and the decentration for a 300 angle of gaze is approximately 15 mm.
Load more

Recommended publications
  • Correlation of the Abbe Number, the Refractive Index, and Glass Transition Temperature to the Degree of Polymerization of Norbornane in Polycarbonate Polymers
    polymers Article Correlation of the Abbe Number, the Refractive Index, and Glass Transition Temperature to the Degree of Polymerization of Norbornane in Polycarbonate Polymers Noriyuki Kato 1,2,*, Shinya Ikeda 1, Manabu Hirakawa 1 and Hiroshi Ito 2,3 1 Mitsubishi Gas Chemical Company, 2-5-2 Marunouchi, Chiyoda-ku, Tokyo 100-8324, Japan; [email protected] (S.I.); [email protected] (M.H.) 2 Graduate School of Science and Engineering, Yamagata University, 4-3-16 Jonan, Yonezawa, Yamagata 992-8510, Japan; [email protected] 3 Graduate School of Organic Materials Science, Yamagata University, 4-3-16 Jonan, Yonezawa, Yamagata 992-8510, Japan * Correspondence: [email protected] Received: 1 September 2020; Accepted: 16 October 2020; Published: 26 October 2020 Abstract: The influences of the average degree of polymerization (Dp), which is derived from Mn and terminal end group, on optical and thermal properties of various refractive indexed transparent polymers were investigated. In this study, we selected the alicyclic compound, Dinorbornane dimethanol (DNDM) homo polymer, because it has been used as a representative monomer in low refractive index polymers for its unique properties. DNDM monomer has a stable amorphous phase and reacts like a polymer. Its unique reaction allows continuous investigation from monomer to polymer. For hydroxy end group and phenolic end group polymers, the refractive index (nd) decreased with increasing Dp, and both converged to same value in the high Dp region. However, the Abbe number (νd) of a hydroxy end group polymer is not dependent on Dp, and the νd of a phenolic end group polymer is greatly dependent on Dp.
    [Show full text]
  • Development of Highly Transparent Zirconia Ceramics
    11 Development of highly transparent zirconia ceramics Isao Yamashita ＊1 Masayuki Kudo ＊1 Koji Tsukuma ＊1 Highly transparent zirconia ceramics were developed and their optical and mechanical properties were comprehensively studied. A low optical haze value (H<1.0 %), defined as the diffuse transmission divided by the total forward transmission, was achieved by using high-purity powder and a novel sintering process. Theoretical in-line transmission (74 %) was observed from the ultraviolet–visible region up to the infra-red region; an absorption edge was found at 350 nm and 8 µm for the ultraviolet and infrared region, respectively. A colorless sintered body having a high refractive index (n d = 2.23) and a high Abbe’s number (νd = 27.8) was obtained. A remarkably large dielectric constant (ε = 32.7) with low dielectric loss (tanδ = 0.006) was found. Transparent zirconia ceramics are candidates for high-refractive index lenses, optoelectric devices and infrared windows. Transparent zirconia ceramics also possess excellent mechanical properties. Various colored transparent zirconia can be used as exterior components and for complex-shaped gemstones. fabricating transparent cubic zirconia ceramics.9,13-19 1．Introduction Transparent zirconia ceramics using titanium oxide as Transparent and translucent ceramics have been a sintering additive were firstly reported by Tsukuma.15 studied extensively ever since the seminal work on However, the sintered body had poor transparency translucent alumina polycrystal by Coble in the 1960s.1 and low mechanical strength. In this study, highly Subsequently, researchers have conducted many transparent zirconia ceramics of high strength were studies to develop transparent ceramics such as MgO,2 developed.
    [Show full text]
  • Trivex & Polycarbonate Lenses
    Trivex Trivex was originally developed for the military, as visual armor. PPG Industries took the technology and adapted it for the optical industry. Trivex is a urethane-based pre-polymer. PPG named the material Trivex because of its three main performance properties. The three main properties are superior optics, ultra- lightweight, and extreme strength. Trivex has a high abbe value. Abbe value is a measure of the dispersion or color distortion of light through a lens into its color elements. Abbe number can also be referred to as v-value. The higher the abbe number, the less dispersion, the lower the number, the more dispersion. Trivex has an abbe number of 43-45. This is significantly higher than polycarbonate. Polycarbonate's abbe number is 30. Trivex has a very high level of light transmittance. The level is 91.4%. This is one of the highest levels of all lens materials. The high percentage is a factor that directly affects the brightness, clarity, and crispness of Trivex. Trivex has a specific gravity of 1.11. Specific gravity is the weight in grams of one cubic centimeter of the material. Specific gravity is also referred to as density. The higher the number, the more dense, or heavy, a lens material is. Trivex has the lowest specific gravity of any commonly used lens material. This makes Trivex the lightest lens material. Trivex is 16% lighter than CR-39, 25% lighter than 1.66, and 8% lighter than polycarbonate! Trivex has a refractive index of 1.53. This allows for a thinner lens than a CR-39 lens.
    [Show full text]
  • Optical Glass
    OPTICAL GLASS JAN. 2020 Contents New Glass Types . 4 3. Chemical Properties . 87 OHARA Group . 21 3 1. Water Resistance RW(p) and Main Products . 22 Acid Resistance RA(p) (Powder Method) . 88 Comparative Table of Optical Glasses, 3 .2 Weathering Resistance W(s) (Surface Method) . 89 Codes and Glass-types . 26 3 .3 Acid Resistance (SR) . 89 3 .4 Phosphate Resistance (PR) . 92 1. Designation of OHARA’s Optical Glass Types . 80 4. Thermal Properties . 93 4 1. Transformation Temperature (Tg), 2. Optical Properties . 81 Yield Point (At) . 93 2 1. Refractive Index . 81 4 .2 Softening Point (SP) . 94 2 2. Dispersion . 82 4 .3 Annealing Point (AP) . 94 2 .3 Partial Dispersion Ratio, Anomalous Dispersion 82 4.4 Linear Coefficient of Thermal Expansion (α) . 94 2 .4 Temperature Coefficient of 4 .5 Thermal Conductivity (k) . 94 Refractive Index (dn/dTrelative) . 83 2 5. Coloring . 85 2.6 Internal Transmittance λ0 .80 / λ 0 .05 . 86 2 .7 CCI . 86 2 5. Mechanical Properties . 95 8. Forms of Supply . 104 5 1. Knoop Hardness (Hk) . 95 8 1. Glass Blocks . 104 5 .2 Abrasion (Aa) . 96 8 .2 Pressings (Reheat Pressings – RP) . 105 8 .3 Saw-cut Centerless Ground Cylindrical 6. Other Properties . 97 Blanks . 107 6.1 Photoelastic Constant (β) . 97 8 .4 Dimensional Specified Blanks . 108 6 .2 Specific Gravity (d) . 97 8 .5 High Homogeneity Blanks . 109 8 .6 Polished Balls . 110 7. Guarantees of Quality . 98 8 7. Polished Preforms . 111 7 1. Refractive Index and Abbe Number . 98 8 .8 Aspherical Glass Mold Lenses .
    [Show full text]
  • Abbe Number 404 Absorption 570 by Transition Metals 234 Edge 333
    INDEX (Bold Type indicates Chapter) A c Cab-O-SiI™ 7 Abbe number 404 Cadmium sulfide 332 Absorption 570 selenide 338 by transition metals 234 telluride 338 edge 333 Calorimetry 209 Acetyl acetonates 159, 176,239 Catalysis 360 Aerogels 23, 96, 366 Catalysts for hydrolysis 41 Aerosol 161 acid 3, 86 ammonia 86, 330 Alumina 160, 170, 376 base 86 Aluminosilicate 302 Catalyst supports 343 Li/Mg0365 Auger electron spectroscopy (AES) 179, 492 Ru/Si02 359 Autoclaving 24 Pd/Si02359 Pt/Ti02363 B Pt-Sn/AI203364 Barium titanate 43 Cerarners 427 BET method 345, 547 Cermet Birefringence 272, 441 silica-precious metal 344 Bloating 26 Chalcogenides 473 Boria 402, 493 Chelating agents b-diketones 44, 259, 457 Boric acid 17 5 glycol 259, 426 Borosilicates 493 Chemical leaching 296, 375 with baria 407 584 Chemical vapor deposition (CVD) 256 Conductivity modified (MCVD) 157 electrical 268 thermal 24 Chlorination 27, 103 Conventional melting 60, 83, 328 Chromophores bipyridyltriscarbonylchloro Copper bromide 340 rhenium (ReCI(CO)3 birpy) 302 Copper chloride 340 DEANST (diethylamino­ nitrostyrene) 429 Coupling efficiency 525 HNPP (N -(3-hydroxy-4-nitro­ phenyl)-(L)-prolinol) Crosslinking 49, 451 429 NPP (N--(4-nitrophenyl)-(L)­ Crystallization 28, 132, 207, 266, 332, prolinol) 429 502 PNA (para-nitroaniline) 420 D Clean room conditions 144,470 Defects Coatings (see also Layers, Thin Films) bubbles 66 adhesion of 268 colored 233 Dehydration conductive 173,269,431 chemical 27, 66, 102 electroc:hromic 178,497 chlorine treatments 27, 103 multilayer 171, 242 thermal
    [Show full text]
  • Teaching Optics
    Optica Applicata. Vol. XXXI, No. 4, 2001 Teaching optics Possibilities of aberration correction in a single spectacle lens M arek Zając Institute of Physics, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland. Spectacle-wearers make up a considerable part of present-day society, so spectacles are one of the most popular optical instruments — very simple instruments since they are in lact single lenses. On the other hand their mode of operation and the demands for imaging quality are very specific. Therefore, spectacle lenses are interesting objects for aberration analysis and are excellent examples for illustrating purposes while teaching geometrical optics. Typically, the spectacle lens is fixed at some distance in front of the eye. When looking at distant objects, the eye rotates around its centre of rotation while the field-of-view angle is limited practically only by the spectacle frame. The chief ray, connecting point of fixation and centre of eye pupil always passes through the eyeball centre of rotation. Therefore we can assume that spectacle lens has shifted output pupil while preserving a relatively large field of view. Consequently, it is important to correct field aberrations, in particular astigmatism. It is interesting to investigate relationships between spherical aberration, coma and field curvature each as a function of output pupil shift and to point out that it is possible to correct fully astigmatism and minimise spherical aberration or coma 1. Introduction For about 700 years spectacles have been used for correction of such vision defects as myopia, hypermetropia, astigmatism or presbyopia. Except for very few cases, single lenses — mainly of spherical or toroidal surfaces — have been used to this aim.
    [Show full text]
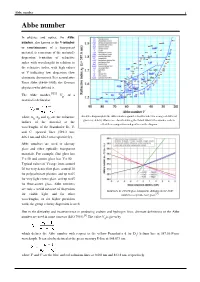
  • Abbe Number 1 Abbe Number
    Abbe number 1 Abbe number In physics and optics, the Abbe number, also known as the V-number or constringence of a transparent material, is a measure of the material's dispersion (variation of refractive index with wavelength) in relation to the refractive index, with high values of V indicating low dispersion (low chromatic aberration). It is named after Ernst Abbe (1840–1905), the German physicist who defined it. The Abbe number,[2][3] V , of a D material is defined as where n , n and n are the refractive An Abbe diagram plots the Abbe number against refractive index for a range of different D F C glasses (red dots). Glasses are classified using the Schott Glass letter-number code to indices of the material at the reflect their composition and position on the diagram. wavelengths of the Fraunhofer D-, F- and C- spectral lines (589.3 nm, 486.1 nm and 656.3 nm respectively). Abbe numbers are used to classify glass and other optically transparent materials. For example, flint glass has V < 50 and crown glass has V > 50. Typical values of V range from around 20 for very dense flint glass, around 30 for polycarbonate plastics, and up to 65 for very light crown glass, and up to 85 for fluor-crown glass. Abbe numbers are only a useful measure of dispersion Influences of selected glass component additions on the Abbe [1] for visible light, and for other number of a specific base glass. wavelengths, or for higher precision work, the group velocity dispersion is used.
    [Show full text]
  • Transparent Ceramics Find Wide Use in Optics
    Transparent Ceramics Find Wide Use in Optics Mohan Ramisetty, Suri A. Sastri and Lee Goldman, Surmet Corp. Polycrystalline ceramics with the cubic spinel structure enable multiple defense applications, including night-vision goggles and IR optics for military systems such as domes, lenses, reconnaissance and sensor windows – they also have applications in nonmilitary arenas such as semiconductor processing, oil and gas drilling, medical optics and lasers. Spinel ceramics have been around for a very long time, and ALON – a ceramic based on a composition of aluminum oxynitride with a cubic spinel crystal structure – has been around for over 50 years. However, until the late 1990s or so, the majority of research related to these materials stayed within the laboratories and academia. Commercialization efforts have taken the fast track in the recent 10 years or so. Thanks to growing interest and efforts from the defense and aerospace industries, both ALON and spinel now are commercially available in the US. This is expected to usher in multiple industrial and civilian applications that can benefit from the unique optical and mechanical properties of ALON and spinel. And these transparent ceramic materials have broad appeal to the precision optics community as well. Several factors are driving the commercial development of ALON and spinel ceramics. At the top of the list are their extreme durability, their high-temperature performance and their superior mechanical properties over glasses, as well as their ease of scalability and manufacturability compared with single crystals such as sapphire. Being polycrystalline – as opposed to a single crystal – makes their fabrication into large and complex shapes using a variety of powder processing approaches easier.
    [Show full text]
  • TIE-29: Refractive Index and Dispersion
    DATE April 2005 . PAGE 1/15 TIE-29: Refractive Index and Dispersion 0. Introduction The most important property of optical glass is the refractive index and its dispersion behavior. This technical information gives an overview of the following topics: - Dispersion o Principal dispersion (page 2) o Secondary spectrum (page 3) o Sellmeier dispersion equation (page 4) - Temperature dependence of refractive index (page 6) - Influence of the fine annealing process on the refractive index and Abbe number (page 9) - Tolerances (page 12) - Refractive index measurement (page 13) 1. Refractive Index If light enters a non-absorbing homogeneous materials reflection and refraction occurs at the boundary surface. The refractive index n is given by the ratio of the velocity of light in vacuum c to that of the medium v c n = (1-1) v The refractive index data given in the glass catalogue are measured relative to the refractive index measured in air. The refractive index of air is very close to 1. Practically speaking the refractive index is a measure for the strength of deflection occurring at the boundary surface due to the refraction of the light beam. The equation describing the amount of deflection is called Snell’s law: n1 × sin(a1) = n2 × sin(a 2 ) (1-2) The refractive index is a function of the wavelength. The most common characteristic quantity for characterization of an optical glass is the refractive index n in the middle range of the visible spectrum. This principal refractive index is usually denoted as nd – the refractive index at the wavelength 587.56 nm or in many cases as ne at the wavelength 546.07 nm.
    [Show full text]
  • Optical Theory Simplified: 9 Fundamentals to Becoming an Optical Genius APPLICATION NOTES
    LEARNING – UNDERSTANDING – INTRODUCING – APPLYING Optical Theory Simplified: 9 Fundamentals To Becoming An Optical Genius APPLICATION NOTES Optics Application Examples Introduction To Prisms Understanding Optical Specifications Optical Cage System Design Examples All About Aspheric Lenses Optical Glass Optical Filters An Introduction to Optical Coatings Why Use An Achromatic Lens www.edmundoptics.com OPTICS APPLICATION EXAMPLES APPLICATION 1: DETECTOR SYSTEMS Every optical system requires some sort of preliminary design. system will help establish an initial plan. The following ques- Getting started with the design is often the most intimidating tions will illustrate the process of designing a simple detector step, but identifying several important specifications of the or emitter system. GOAL: WHERE WILL THE LIGHT GO? Although simple lenses are often used in imaging applications, such as a plano-convex (PCX) lens or double-convex (DCX) in many cases their goal is to project light from one point to lens, can be used. another within a system. Nearly all emitters, detectors, lasers, and fiber optics require a lens for this type of light manipula- Figure 1 shows a PCX lens, along with several important speci- tion. Before determining which type of system to design, an fications: Diameter of the lens (D1) and Focal Length (f). Figure important question to answer is “Where will the light go?” If 1 also illustrates how the diameter of the detector limits the the goal of the design is to get all incident light to fill a detector, Field of View (FOV) of the system, as shown by the approxi- with as few aberrations as possible, then a simple singlet lens, mation for Full Field of View (FFOV): (1.1) D Figure 1: 1 D θ PCX Lens as FOV Limit FF0V = 2 β in Detector Application ƒ Detector (D ) 2 or, by the exact equation: (1.2) / Field of View (β) -1 D FF0V = 2 tan ( 2 ) f 2ƒ For detectors used in scanning systems, the important mea- sure is the Instantaneous Field of View (IFOV), which is the angle subtended by the detector at any instant during scan- ning.
    [Show full text]
  • Optical Properties of Diamond
    MICHAEL E. THOMAS and WILLIAM J. TROPF OPTICAL PROPERTIES OF DIAMOND Diamond offers unique properties for optical elements and coatings. This article reviews the properties of diamond and presents the results of recent measurements and efforts in the modeling of its optical properties at the Applied Physics Laboratory. INTRODUCTION TYPES OF DIAMONDS In the past, the commercial use of diamonds was re­ Four classifications of natural diamond have been made stricted to poor optical quality "industrial diamonds" for on the basis of optical properties. Only Type IIa is suitable cutting and grinding. These diamonds were either natural for infrared optics. diamonds unsuitable for gems or were manufactured by Type fa accounts for 95 to 98% of natural diamond and subjecting graphite, the stable form of carbon at ambient contains substantial nitrogen impurity (up to 0.2%), which conditions, to intense pressure and temperature. The use forms in aggregates or platelets. This type of diamond has of diamond as an optical material was restricted to a few strong absorption below 320 nm, low thermal conductivity specialized applications such as planetary radiometry «9 W/[m·K]), and high electrical resistivity (> 10 14 n·m). from satellites (e.g., Nimbus and the Pioneer series) and Type fb also has substantial nitrogen but in a dispersed high-pressure cells ("diamond anvils"). Recent progress substitutional form. The nitrogen imparts color, ranging in the manufacture of high-quality diamonds through the from pale yellow to green, depending on nitrogen concen­ chemical vapor deposition (CVD) process opens the pos­ tration. Synthetic industrial diamonds are typically Type lb.
    [Show full text]
  • Optical Properties of Makrolon® and Apec® for Non-Imaging Optics
    Optical properties of Makrolon® and Apec® for non-imaging optics 1 Introduction A | Nomenclature 03 1 Introduction B | Color designation 03 Makrolon® and Apec® polycarbonates from Covestro are characterized by a combination of crystal clear 2 Clear, transparent Makrolon® grades 04 A | Transmission spectra 05 transparency, high heat resistance, high strength B | Refractive index 07 and good flame retardant properties. This brochure C | Weathering properties 08 mainly describes the optical properties of Makrolon® D | Temperature resistance 10 E | Aging under artificial light sources 11 and Apec®, and how they are affected by temperature and UV light. However, a brochure of this kind can 3 Signal colors 12 only cover a limited selection of the diverse sets 4 High-reflectance white 15 of requirements. In its polycarbonates portfolio, 5 Special colors 16 Covestro distinguishes optical Makrolon® grades and A | NIR-transparent black 16 other specialty grades, such as the high-temperature B | NIR-absorbing grades 16 polycarbonate Apec®, from the standard Makrolon® C | Laser-marking colors 16 grades. This brochure focuses on the optical proper- 6 Translucent grades 17 ties of the optical Makrolon® and Apec® grades. 7 Apec® – High-temperature- resistant Polycarbonate 21 8 Appendix – Typical properties of Makrolon® and Apec® 24 2 | OPTICAL PROPERTIES OF MAKROLON® AND APEC® All values are typical, not specified values. A | Nomenclature The following system of nomenclature is used for most Makrolon® and Apec® grades: The designation of Makrolon® and Apec® sales products are based on a 4-digit, self-explanatory nomenclature. Makrolon® LED 22 4 5 Apec® 20 9 7 The first two digits denote the viscosity: The first two digits denote the heat resistance: 22 low viscosity 16 Vicat approx.
    [Show full text]