Efficient Two-Component Relativistic Method to Obtain Electronic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chem Compute Quickstart
Chem Compute Quickstart Chem Compute is maintained by Mark Perri at Sonoma State University and hosted on Jetstream at Indiana University. The Chem Compute URL is https://chemcompute.org/. We will use Chem Compute as the frontend for running electronic structure calculations with The General Atomic and Molecular Electronic Structure System, GAMESS (http://www.msg.ameslab.gov/gamess/). Chem Compute also provides access to other computational chemistry resources including PSI4 and the molecular dynamics packages TINKER and NAMD, though we will not be using those resource at this time. Follow this link, https://chemcompute.org/gamess/submit, to directly access the Chem Compute GAMESS guided submission interface. If you are a returning Chem Computer user, please log in now. If your University is part of the InCommon Federation you can log in without registering by clicking Login then "Log In with Google or your University" – select your University from the dropdown list. Otherwise if this is your first time working with Chem Compute, please register as a Chem Compute user by clicking the “Register” link in the top-right corner of the page. This gives you access to all of the computational resources available at ChemCompute.org and will allow you to maintain copies of your calculations in your user “Dashboard” that you can refer to later. Registering also helps track usage and obtain the resources needed to continue providing its service. When logged in with the GAMESS-Submit tabs selected, an instruction section appears on the left side of the page with instructions for several different kinds of calculations. -

Parameterizing a Novel Residue
University of Illinois at Urbana-Champaign Luthey-Schulten Group, Department of Chemistry Theoretical and Computational Biophysics Group Computational Biophysics Workshop Parameterizing a Novel Residue Rommie Amaro Brijeet Dhaliwal Zaida Luthey-Schulten Current Editors: Christopher Mayne Po-Chao Wen February 2012 CONTENTS 2 Contents 1 Biological Background and Chemical Mechanism 4 2 HisH System Setup 7 3 Testing out your new residue 9 4 The CHARMM Force Field 12 5 Developing Topology and Parameter Files 13 5.1 An Introduction to a CHARMM Topology File . 13 5.2 An Introduction to a CHARMM Parameter File . 16 5.3 Assigning Initial Values for Unknown Parameters . 18 5.4 A Closer Look at Dihedral Parameters . 18 6 Parameter generation using SPARTAN (Optional) 20 7 Minimization with new parameters 32 CONTENTS 3 Introduction Molecular dynamics (MD) simulations are a powerful scientific tool used to study a wide variety of systems in atomic detail. From a standard protein simulation, to the use of steered molecular dynamics (SMD), to modelling DNA-protein interactions, there are many useful applications. With the advent of massively parallel simulation programs such as NAMD2, the limits of computational anal- ysis are being pushed even further. Inevitably there comes a time in any molecular modelling scientist’s career when the need to simulate an entirely new molecule or ligand arises. The tech- nique of determining new force field parameters to describe these novel system components therefore becomes an invaluable skill. Determining the correct sys- tem parameters to use in conjunction with the chosen force field is only one important aspect of the process. -
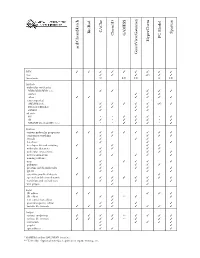
D:\Doc\Workshops\2005 Molecular Modeling\Notebook Pages\Software Comparison\Summary.Wpd
CAChe BioRad Spartan GAMESS Chem3D PC Model HyperChem acd/ChemSketch GaussView/Gaussian WIN TTTT T T T T T mac T T T (T) T T linux/unix U LU LU L LU Methods molecular mechanics MM2/MM3/MM+/etc. T T T T T Amber T T T other TT T T T T semi-empirical AM1/PM3/etc. T T T T T (T) T Extended Hückel T T T T ZINDO T T T ab initio HF * * T T T * T dft T * T T T * T MP2/MP4/G1/G2/CBS-?/etc. * * T T T * T Features various molecular properties T T T T T T T T T conformer searching T T T T T crystals T T T data base T T T developer kit and scripting T T T T molecular dynamics T T T T molecular interactions T T T T movies/animations T T T T T naming software T nmr T T T T T polymers T T T T proteins and biomolecules T T T T T QSAR T T T T scientific graphical objects T T spectral and thermodynamic T T T T T T T T transition and excited state T T T T T web plugin T T Input 2D editor T T T T T 3D editor T T ** T T text conversion editor T protein/sequence editor T T T T various file formats T T T T T T T T Output various renderings T T T T ** T T T T various file formats T T T T ** T T T animation T T T T T graphs T T spreadsheet T T T * GAMESS and/or GAUSSIAN interface ** Text only. -
![Arxiv:1710.00259V1 [Physics.Chem-Ph] 30 Sep 2017 a Relativistically Correct Electron Interaction](https://docslib.b-cdn.net/cover/2561/arxiv-1710-00259v1-physics-chem-ph-30-sep-2017-a-relativistically-correct-electron-interaction-842561.webp)
Arxiv:1710.00259V1 [Physics.Chem-Ph] 30 Sep 2017 a Relativistically Correct Electron Interaction
One-step treatment of spin-orbit coupling and electron correlation in large active spaces Bastien Mussard1, ∗ and Sandeep Sharma1, y 1Department of Chemistry and Biochemistry, University of Colorado Boulder, Boulder, CO 80302, USA In this work we demonstrate that the heat bath configuration interaction (HCI) and its semis- tochastic extension can be used to treat relativistic effects and electron correlation on an equal footing in large active spaces to calculate the low energy spectrum of several systems including halogens group atoms (F, Cl, Br, I), coinage atoms (Cu, Au) and the Neptunyl(VI) dioxide radical. This work demonstrates that despite a significant increase in the size of the Hilbert space due to spin symmetry breaking by the spin-orbit coupling terms, HCI retains the ability to discard large parts of the low importance Hilbert space to deliver converged absolute and relative energies. For instance, by using just over 107 determinants we get converged excitation energies for Au atom in an active space containing (150o,25e) which has over 1030 determinants. We also investigate the accuracy of five different two-component relativistic Hamiltonians in which different levels of ap- proximations are made in deriving the one-electron and two-electrons Hamiltonians, ranging from Breit-Pauli (BP) to various flavors of exact two-component (X2C) theory. The relative accuracy of the different Hamiltonians are compared on systems that range in atomic number from first row atoms to actinides. I. INTRODUCTION can become large and it is more appropriate to treat them on an equal footing with the spin-free terms and electron Relativistic effects play an important role in a correlation. -

Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C
Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C. All rights reserved. Schrödinger, FirstDiscovery, Glide, Impact, Jaguar, Liaison, LigPrep, Maestro, Prime, QSite, and QikProp are trademarks of Schrödinger, L.L.C. MacroModel is a registered trademark of Schrödinger, L.L.C. To the maximum extent permitted by applicable law, this publication is provided “as is” without warranty of any kind. This publication may contain trademarks of other companies. October 2003 Contents Chapter 1: Introduction.......................................................................................1 1.1 Conventions Used in This Manual.......................................................................2 1.2 Citing Jaguar in Publications ...............................................................................3 Chapter 2: The Maestro Graphical User Interface...........................................5 2.1 Starting Maestro...................................................................................................5 2.2 The Maestro Main Window .................................................................................7 2.3 Maestro Projects ..................................................................................................7 2.4 Building a Structure.............................................................................................9 2.5 Atom Selection ..................................................................................................10 2.6 Toolbar Controls ................................................................................................11 -

CHEM:4480 Introduction to Molecular Modeling
CHEM:4480:001 Introduction to Molecular Modeling Fall 2018 Instructor Dr. Sara E. Mason Office: W339 CB, Phone: (319) 335-2761, Email: [email protected] Lecture 11:00 AM - 12:15 PM, Tuesday/Thursday. Primary Location: W228 CB. Please note that we will often meet in one of the Chemistry Computer Labs. Notice about class being held outside of the primary location will be posted to the course ICON site by 24 hours prior to the start of class. Office Tuesday 12:30-2 PM (EXCEPT for DoC faculty meeting days 9/4, 10/2, 10/9, 11/6, Hour and 12/4), Thursday 12:30-2, or by appointment Department Dr. James Gloer DEO Administrative Office: E331 CB Administrative Phone: (319) 335-1350 Administrative Email: [email protected] Text Instead of a course text, assigned readings will be given throughout the semester in forms such as journal articles or library reserves. Website http://icon.uiowa.edu Course To develop practical skills associated with chemical modeling based on quantum me- Objectives chanics and computational chemistry such as working with shell commands, math- ematical software, and modeling packages. We will also work to develop a basic understanding of quantum mechanics, approximate methods, and electronic struc- ture. Technical computing, pseudopotential generation, density functional theory software, (along with other optional packages) will be used hands-on to gain experi- ence in data manipulation and modeling. We will use both a traditional classroom setting and hands-on learning in computer labs to achieve course goals. Course Topics • Introduction: It’s a quantum world! • Dirac notation and matrix mechanics (a.k.a. -

Porting the DFT Code CASTEP to Gpgpus
Porting the DFT code CASTEP to GPGPUs Toni Collis [email protected] EPCC, University of Edinburgh CASTEP and GPGPUs Outline • Why are we interested in CASTEP and Density Functional Theory codes. • Brief introduction to CASTEP underlying computational problems. • The OpenACC implementation http://www.nu-fuse.com CASTEP: a DFT code • CASTEP is a commercial and academic software package • Capable of Density Functional Theory (DFT) and plane wave basis set calculations. • Calculates the structure and motions of materials by the use of electronic structure (atom positions are dictated by their electrons). • Modern CASTEP is a re-write of the original serial code, developed by Universities of York, Durham, St. Andrews, Cambridge and Rutherford Labs http://www.nu-fuse.com CASTEP: a DFT code • DFT/ab initio software packages are one of the largest users of HECToR (UK national supercomputing service, based at University of Edinburgh). • Codes such as CASTEP, VASP and CP2K. All involve solving a Hamiltonian to explain the electronic structure. • DFT codes are becoming more complex and with more functionality. http://www.nu-fuse.com HECToR • UK National HPC Service • Currently 30- cabinet Cray XE6 system – 90,112 cores • Each node has – 2×16-core AMD Opterons (2.3GHz Interlagos) – 32 GB memory • Peak of over 800 TF and 90 TB of memory http://www.nu-fuse.com HECToR usage statistics Phase 3 statistics (Nov 2011 - Apr 2013) Ab initio codes (VASP, CP2K, CASTEP, ONETEP, NWChem, Quantum Espresso, GAMESS-US, SIESTA, GAMESS-UK, MOLPRO) GS2NEMO ChemShell 2%2% SENGA2% 3% UM Others 4% 34% MITgcm 4% CASTEP 4% GROMACS 6% DL_POLY CP2K VASP 5% 8% 19% http://www.nu-fuse.com HECToR usage statistics Phase 3 statistics (Nov 2011 - Apr 2013) 35% of the Chemistry software on HECToR is using DFT methods. -
Massive-Parallel Implementation of the Resolution-Of-Identity Coupled
Article Cite This: J. Chem. Theory Comput. 2019, 15, 4721−4734 pubs.acs.org/JCTC Massive-Parallel Implementation of the Resolution-of-Identity Coupled-Cluster Approaches in the Numeric Atom-Centered Orbital Framework for Molecular Systems † § † † ‡ § § Tonghao Shen, , Zhenyu Zhu, Igor Ying Zhang,*, , , and Matthias Scheffler † Department of Chemistry, Fudan University, Shanghai 200433, China ‡ Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, MOE Key Laboratory of Computational Physical Science, Fudan University, Shanghai 200433, China § Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany *S Supporting Information ABSTRACT: We present a massive-parallel implementation of the resolution of identity (RI) coupled-cluster approach that includes single, double, and perturbatively triple excitations, namely, RI-CCSD(T), in the FHI-aims package for molecular systems. A domain-based distributed-memory algorithm in the MPI/OpenMP hybrid framework has been designed to effectively utilize the memory bandwidth and significantly minimize the interconnect communication, particularly for the tensor contraction in the evaluation of the particle−particle ladder term. Our implementation features a rigorous avoidance of the on- the-fly disk storage and excellent strong scaling of up to 10 000 and more cores. Taking a set of molecules with different sizes, we demonstrate that the parallel performance of our CCSD(T) code is competitive with the CC implementations in state-of- the-art high-performance-computing computational chemistry packages. We also demonstrate that the numerical error due to the use of RI approximation in our RI-CCSD(T) method is negligibly small. Together with the correlation-consistent numeric atom-centered orbital (NAO) basis sets, NAO-VCC-nZ, the method is applied to produce accurate theoretical reference data for 22 bio-oriented weak interactions (S22), 11 conformational energies of gaseous cysteine conformers (CYCONF), and 32 Downloaded via FRITZ HABER INST DER MPI on January 8, 2021 at 22:13:06 (UTC). -

US DOE SC ASCR FY11 Software Effectiveness SC GG 3.1/2.5.2 Improve Computational Science Capabilities
US DOE SC ASCR FY11 Software Effectiveness SC GG 3.1/2.5.2 Improve Computational Science Capabilities K. J. Roche High Performance Computing Group, Pacific Northwest National Laboratory Nuclear Theory Group, Department of Physics, University of Washington Presentation to ASCAC, Washington, D.C. , November 2, 2011 Tuesday, November 1, 2011 1 LAMMPS Paul Crozier, Steve Plimpton, Mark Brown, Christian Trott OMEN, NEMO 5 Gerhard Klimeck, Mathieu Luisier, Sebastian Steiger, Michael Povolotskyi, Hong-Hyun Park, Tillman Kubis OSIRIS Warren Mori, Ricardo Fonseca, Asher Davidson, Frank Tsung, Jorge Vieira, Frederico Fiuza, Panagiotis Spentzouris eSTOMP Steve Yabusaki, Yilin Fang, Bruce Palmer, Manojkumar Krishnan Rebecca Hartman-Baker Ricky Kendall Don Maxwell Bronson Messer Vira j Paropkari David Skinner Jack Wells Cary Whitney Rice HPC Toolkit group DOE ASCR, OLCF and NERSC staf Tuesday, November 1, 2011 2 • Metric Statement, Processing • FY11 Applications Intro Problems Enhancements Results • FY12 Nominations Tuesday, November 1, 2011 3 US OMB PART DOE SC ASCR Annual Goal with Quarterly Updates (SC GG 3.1/2.5.2) Improve computational science capabilities, defined as the average annual percentage increase in the computational effectiveness (either by simulating the same problem in less time or simulating a larger problem in the same time) of a subset of application codes. To those ‘on the clock’ with this work, it means more than just satisfying the language of this metric. Tuesday, November 1, 2011 4 accept • COMPLEXITY LP LR PROBLEMS M M M • reject • ALGORITHMS • MACHINES Measured time for machine M to generate the language of the problem plus time to generate the language of the result plus the time to accept or reject the language of the result. -

Lawrence Berkeley National Laboratory Recent Work
Lawrence Berkeley National Laboratory Recent Work Title From NWChem to NWChemEx: Evolving with the Computational Chemistry Landscape. Permalink https://escholarship.org/uc/item/4sm897jh Journal Chemical reviews, 121(8) ISSN 0009-2665 Authors Kowalski, Karol Bair, Raymond Bauman, Nicholas P et al. Publication Date 2021-04-01 DOI 10.1021/acs.chemrev.0c00998 Peer reviewed eScholarship.org Powered by the California Digital Library University of California From NWChem to NWChemEx: Evolving with the computational chemistry landscape Karol Kowalski,y Raymond Bair,z Nicholas P. Bauman,y Jeffery S. Boschen,{ Eric J. Bylaska,y Jeff Daily,y Wibe A. de Jong,x Thom Dunning, Jr,y Niranjan Govind,y Robert J. Harrison,k Murat Keçeli,z Kristopher Keipert,? Sriram Krishnamoorthy,y Suraj Kumar,y Erdal Mutlu,y Bruce Palmer,y Ajay Panyala,y Bo Peng,y Ryan M. Richard,{ T. P. Straatsma,# Peter Sushko,y Edward F. Valeev,@ Marat Valiev,y Hubertus J. J. van Dam,4 Jonathan M. Waldrop,{ David B. Williams-Young,x Chao Yang,x Marcin Zalewski,y and Theresa L. Windus*,r yPacific Northwest National Laboratory, Richland, WA 99352 zArgonne National Laboratory, Lemont, IL 60439 {Ames Laboratory, Ames, IA 50011 xLawrence Berkeley National Laboratory, Berkeley, 94720 kInstitute for Advanced Computational Science, Stony Brook University, Stony Brook, NY 11794 ?NVIDIA Inc, previously Argonne National Laboratory, Lemont, IL 60439 #National Center for Computational Sciences, Oak Ridge National Laboratory, Oak Ridge, TN 37831-6373 @Department of Chemistry, Virginia Tech, Blacksburg, VA 24061 4Brookhaven National Laboratory, Upton, NY 11973 rDepartment of Chemistry, Iowa State University and Ames Laboratory, Ames, IA 50011 E-mail: [email protected] 1 Abstract Since the advent of the first computers, chemists have been at the forefront of using computers to understand and solve complex chemical problems. -

Computational Chemistry
Computational Chemistry as a Teaching Aid Melissa Boule Aaron Harshman Rexford Hoadley An Interactive Qualifying Project Report Submitted to the Faculty of the Worcester Polytechnic Institute In partial fulfillment of the requirements for the Bachelor of Science Degree Approved by: Professor N. Aaron Deskins 1i Abstract Molecular modeling software has transformed the capabilities of researchers. Molecular modeling software has the potential to be a helpful teaching tool, though as of yet its efficacy as a teaching technique has yet to be proven. This project focused on determining the effectiveness of a particular molecular modeling software in high school classrooms. Our team researched what topics students struggled with, surveyed current high school chemistry teachers, chose a modeling software, and then developed a lesson plan around these topics. Lastly, we implemented the lesson in two separate high school classrooms. We concluded that these programs show promise for the future, but with the current limitations of high school technology, these tools may not be as impactful. 2ii Acknowledgements This project would not have been possible without the help of many great educators. Our advisor Professor N. Aaron Deskins provided driving force to ensure the research ran smoothly and efficiently. Mrs. Laurie Hanlan and Professor Drew Brodeur provided insight and guidance early in the development of our topic. Mr. Mark Taylor set-up our WebMO server and all our other technology needs. Lastly, Mrs. Pamela Graves and Mr. Eric Van Inwegen were instrumental by allowing us time in their classrooms to implement our lesson plans. Without the support of this diverse group of people this project would never have been possible. -

The Electron Affinity of the Uranium Atom
The electron affinity of the uranium atom Cite as: J. Chem. Phys. 154, 224307 (2021); https://doi.org/10.1063/5.0046315 Submitted: 02 February 2021 . Accepted: 18 May 2021 . Published Online: 10 June 2021 Sandra M. Ciborowski, Gaoxiang Liu, Moritz Blankenhorn, Rachel M. Harris, Mary A. Marshall, Zhaoguo Zhu, Kit H. Bowen, and Kirk A. Peterson ARTICLES YOU MAY BE INTERESTED IN Ultrahigh sensitive transient absorption spectrometer Review of Scientific Instruments 92, 053002 (2021); https://doi.org/10.1063/5.0048115 A dual-magneto-optical-trap atom gravity gradiometer for determining the Newtonian gravitational constant Review of Scientific Instruments 92, 053202 (2021); https://doi.org/10.1063/5.0040701 How accurate is the determination of equilibrium structures for van der Waals complexes? The dimer N2O⋯CO as an example The Journal of Chemical Physics 154, 194302 (2021); https://doi.org/10.1063/5.0048603 J. Chem. Phys. 154, 224307 (2021); https://doi.org/10.1063/5.0046315 154, 224307 © 2021 Author(s). The Journal ARTICLE of Chemical Physics scitation.org/journal/jcp The electron affinity of the uranium atom Cite as: J. Chem. Phys. 154, 224307 (2021); doi: 10.1063/5.0046315 Submitted: 2 February 2021 • Accepted: 18 May 2021 • Published Online: 10 June 2021 Sandra M. Ciborowski,1 Gaoxiang Liu,1 Moritz Blankenhorn,1 Rachel M. Harris,1 Mary A. Marshall,1 Zhaoguo Zhu,1 Kit H. Bowen,1,a) and Kirk A. Peterson2,a) AFFILIATIONS 1 Department of Chemistry, Johns Hopkins University, Baltimore, Maryland 21218, USA 2 Department of Chemistry, Washington State University, Pullman, Washington 99162, USA a)Authors to whom correspondence should be addressed: [email protected] and [email protected] ABSTRACT The results of a combined experimental and computational study of the uranium atom are presented with the aim of determining its electron affinity.