DOCSLIB.ORG

Big Bang Nucleosynthesis Finally, Relative Abundances Are Sensitive to Density of Normal (Baryonic Matter)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Big Bang Nucleosynthesis Finally, Relative Abundances Are Sensitive to Density of Normal (Baryonic Matter) Big Bang Nucleosynthesis Finally, relative abundances are sensitive to density of normal (baryonic matter) Thus Ωb,0 ~ 4%. So our universe Ωtotal ~1 with 70% in Dark Energy, 30% in matter but only 4% baryonic! Case for the Hot Big Bang • The Cosmic Microwave Background has an isotropic blackbody spectrum – it is extremely difficult to generate a blackbody background in other models • The observed abundances of the light isotopes are reasonably consistent with predictions – again, a hot initial state is the natural way to generate these • Many astrophysical populations (e.g. quasars) show strong evolution with redshift – this certainly argues against any Steady State models The Accelerating Universe Distant SNe appear too faint, must be further away than in a non-accelerating universe. Perlmutter et al. 2003 Riese 2000 Outstanding problems • Why is the CMB so isotropic? – horizon distance at last scattering << horizon distance now – why would causally disconnected regions have the same temperature to 1 part in 105? • Why is universe so flat? – if Ω is not 1, Ω evolves rapidly away from 1 in radiation or matter dominated universe – but CMB analysis shows Ω = 1 to high accuracy – so either Ω=1 (why?) or Ω is fine tuned to very nearly 1 • How do structures form? – if early universe is so very nearly uniform Astronomy 422 Lecture 22: Early Universe Key concepts: Problems with Hot Big Bang Inflation Announcements: April 26: Exam 3 April 28: Presentations begin Astro 422 Presentations: Thursday April 28: 9:30 – 9:50 _Isaiah Santistevan__________ 9:50 – 10:10 _Cameron Trapp____________ 10:10 – 10:30 _Jessica Lopez____________ Tuesday May 3: 9:30 – 9:50 __Chris Quintana____________ 9:50 – 10:10 __Austin Vaitkus___________ 10:10 – 10:30 __Kathryn Jackson__________ Thursday May 5: 9:30 – 9:50 _Montie Avery_______________ 9:50 – 10:10 _Andrea Tallbrother_________ 10:10 – 10:30 _Veronica Dike_____________ 10:30 – 10:50 _Kirtus Leyba________________________ Send me your preference. First come, first served. Main goals • With cosmology we aim to get a physical description of the universe. – What is the matter content? – What is the dynamics of the universe? • We have worked on a set of equations describing the universe, and we introduced a number of cosmological parameters. – Hubble parameter, scale factor, density parameter etc. • We would like to measure these parameters to get the theories right. • Eventually, we use the models to understand the origin and evolution of cosmic structure. Epochs • Friedmann's equation can be written as (Eq. 29.122): • At very early times, when R<<1, only the first two terms are important. • Radiation dominates until z~40000 • CMB released at z~1100 which is well into the matter dominated era. Planck units • GR expected to break down as Big Bang is approached • The estimate for onset of quantum mechanical effects on spacetime is when the de Broglie wavelength equals the Schwarzschild radius: • This defines what we call the Planck mass • We then define the Planck Length : • and the corresponding Planck time: • This corresponds to the earliest time that we can address by current physical theory. Our theories include a set of fundamental constants, and these are the limits of current theories. Horizon problem Start with the Horizon distance (recap) • Universe expands and ages, an observer at any point is able to see more distant objects (light has time to arrive) • As time increases, larger and larger regions of the universe come into causal contact with the observer • The proper distance to the farthest observable point at a time t is called the horizon distance, dh. – Two points separated by a distance > dh are not in causal contact – dh is the diameter of the largest causally connected region. Illustration: causal contact Insufficient time for signal to reach central observer Consider 3 locations in space, A, B & C. A&B are causally connected. A B C Particle horizon Causality problem: how can structures on large scale in the CMB know about each other? How did the temperature get so uniform? Flatness Friedmann's equation again implying during the matter-dominated era, we had • Then we achieve i.e., deviation of the total density parameter from unity grows with time. • Fine-tuning problem: example, if today At the Planck time, This is what we refer to as the flatness problem. Structure problem • Structure in the universe (galaxies, clusters of galaxies etc) came from inhomogeneities in the early universe. • We see those same inhomogeneities in the CMB maps • How was this coherence achieved? • How did the structures get there? • Why are they just the right magnitude and size to produce the structures we see today? • How is it possible to have the same kind of inhomogeneities spread through the whole universe without causal contact between different parts of the early universe? – CMB is statistically the same in all directions – Galaxies that are formed are similar in properties on opposite sides of the universe The relic problem • Analogy: consider cooling of a liquid like water • Once liquid reaches freezing point: – freezing does not occur smoothly and uniformly – starts at certain locations, and the crystals starts growing – when crystals merge to form solid, there will be dislocations where individual crystals meet • The process of freezing is called a phase transition, that is when matter is changing from one phase to another. Example: dislocations in steel • This could produce exotic structures that we call topological effects – domain walls (2d sheet-like structures) – cosmic strings (1d string-like structures) – None of these have been seen in the observable universe (good limits from CMB data: strings would gravitationally lens the background) • GUTs also predict exotic particles produced in the early universe – magnetic monopoles – never detected, and don't reveal their presence in any observed phenomena • The absence of monopoles (and other relics predicted by particle physics theories) is called the relic problem. Summary of problems with the Hot Big Bang model: • Horizon problem – how could the CMB acquire a single temperature across the sky? – causality: how can structures in the CMB know about each other? • Flatness problem – how could the density parameter be fine-tuned such that today? • The relic problem – where are all the magnetic monopoles predicted? • Origin of structure – How could structure arise in this very smooth universe In principle, the purpose of inflation is to create a large, flat, homogenous universe. • Theory of cosmic inflation was first suggested by Alan Guth in 1982 • He postulated an inflationary epoch – very rapid, exponential expansion of the universe – occurs during the first 10-37-10-32 sec – During this time, the universe expanded by a factor of 1040-10100 • Inflation and the radius of the observable universe That would correspond to a drop in the density parameter time Start of End of Now Distant inflation inflation future Timeline: Does this rapid expansion imply a violation of relativity? No, because it is space itself that is expanding, R(t), rather than material particles moving apart at high speed in a fixed, stationary space. Solving cosmological problems with inflation • The flatness problem: – take any reasonably curved surface – expand it by enormous factor – after expansion it look flat locally – so inflation predicts a universe that is indistinguishable from being flat The horizon problem (without inflation) How does inflation solve the horizon problem? • Before inflation, the particle horizon is about 10-29m – determines causally connected region • After inflation, the particle horizon is about 1011 (up to 1070) m – normal expansion takes over, and expands by another factor 1022 before the epoch of last scattering surface – Thus causally connected regions have sizes of at least 1033m! • Since decoupling, the scale factor have increased by at least a factor of 1000 (since z=1100 at decoupling), so the causally connected radius would be 1036 m – Current horizon of the universe is about 1026 m. – Thus, the observable universe is a small part of the causally connected part of the early universe! How inflation solves the structure problem: • Initial inhomogeneities due to quantum fluctuations during inflationary epoch. • Virtual particle pairs that formed would be separated by inflationary expansion before they could annihilate, creating uneven densities. • Inhomogeneities were continually created, and then stretched to much larger scales, outside the horizon • This naturally gives a characteristic power spectrum for the inhomogeneities • Fluctuations created by inflation can only grow at much later times – the particle horizon must expand so that is larger than the size scale of that fluctuation – since the particle horizon increases with time, the smaller scale fluctuations grow first – clusters, voids, are results of quantum fluctuations originally occurring on tiny scales! How inflation solves the relic problem • Suppose you have exotic particles, or structures (cosmic strings, magnetic monopoles etc) created in the very early universe • They would become very diluted during the inflationary epoch, since the space expanded enormously – The probability that we see a relic exotic particle is then very small. • Hm, what about baryons then? Wouldn’t there be a very small probability of finding them as well? – No, because baryogenesis occurred after inflation, it was too hot before. Vacuum energy is converted to regular matter, including baryons, and radiation. Why did inflation happen? The answer
Load more

Recommended publications
  • Inflation and the Theory of Cosmological Perturbations
    Inflation and the Theory of Cosmological Perturbations A. Riotto INFN, Sezione di Padova, via Marzolo 8, I-35131, Padova, Italy. Abstract These lectures provide a pedagogical introduction to inflation and the theory of cosmological per- turbations generated during inflation which are thought to be the origin of structure in the universe. Lectures given at the: Summer School on arXiv:hep-ph/0210162v2 30 Jan 2017 Astroparticle Physics and Cosmology Trieste, 17 June - 5 July 2002 1 Notation A few words on the metric notation. We will be using the convention (−; +; +; +), even though we might switch time to time to the other option (+; −; −; −). This might happen for our convenience, but also for pedagogical reasons. Students should not be shielded too much against the phenomenon of changes of convention and notation in books and articles. Units We will adopt natural, or high energy physics, units. There is only one fundamental dimension, energy, after setting ~ = c = kb = 1, [Energy] = [Mass] = [Temperature] = [Length]−1 = [Time]−1 : The most common conversion factors and quantities we will make use of are 1 GeV−1 = 1:97 × 10−14 cm=6:59 × 10−25 sec, 1 Mpc= 3.08×1024 cm=1.56×1038 GeV−1, 19 MPl = 1:22 × 10 GeV, −1 −1 −42 H0= 100 h Km sec Mpc =2.1 h × 10 GeV, 2 −29 −3 2 4 −3 2 −47 4 ρc = 1:87h · 10 g cm = 1:05h · 10 eV cm = 8:1h × 10 GeV , −13 T0 = 2:75 K=2.3×10 GeV, 2 Teq = 5:5(Ω0h ) eV, Tls = 0:26 (T0=2:75 K) eV.
    [Show full text]
  • Arxiv:Hep-Ph/9912247V1 6 Dec 1999 MGNTV COSMOLOGY IMAGINATIVE Abstract
    IMAGINATIVE COSMOLOGY ROBERT H. BRANDENBERGER Physics Department, Brown University Providence, RI, 02912, USA AND JOAO˜ MAGUEIJO Theoretical Physics, The Blackett Laboratory, Imperial College Prince Consort Road, London SW7 2BZ, UK Abstract. We review1 a few off-the-beaten-track ideas in cosmology. They solve a variety of fundamental problems; also they are fun. We start with a description of non-singular dilaton cosmology. In these scenarios gravity is modified so that the Universe does not have a singular birth. We then present a variety of ideas mixing string theory and cosmology. These solve the cosmological problems usually solved by inflation, and furthermore shed light upon the issue of the number of dimensions of our Universe. We finally review several aspects of the varying speed of light theory. We show how the horizon, flatness, and cosmological constant problems may be solved in this scenario. We finally present a possible experimental test for a realization of this theory: a test in which the Supernovae results are to be combined with recent evidence for redshift dependence in the fine structure constant. arXiv:hep-ph/9912247v1 6 Dec 1999 1. Introduction In spite of their unprecedented success at providing causal theories for the origin of structure, our current models of the very early Universe, in partic- ular models of inflation and cosmic defect theories, leave several important issues unresolved and face crucial problems (see [1] for a more detailed dis- cussion). The purpose of this chapter is to present some imaginative and 1Brown preprint BROWN-HET-1198, invited lectures at the International School on Cosmology, Kish Island, Iran, Jan.
    [Show full text]
  • Inflationary Cosmology: from Theory to Observations
    Inflationary Cosmology: From Theory to Observations J. Alberto V´azquez1, 2, Luis, E. Padilla2, and Tonatiuh Matos2 1Instituto de Ciencias F´ısicas,Universidad Nacional Aut´onomade Mexico, Apdo. Postal 48-3, 62251 Cuernavaca, Morelos, M´exico. 2Departamento de F´ısica,Centro de Investigaci´ony de Estudios Avanzados del IPN, M´exico. February 10, 2020 Abstract The main aim of this paper is to provide a qualitative introduction to the cosmological inflation theory and its relationship with current cosmological observations. The inflationary model solves many of the fundamental problems that challenge the Standard Big Bang cosmology, such as the Flatness, Horizon, and the magnetic Monopole problems. Additionally, it provides an explanation for the initial conditions observed throughout the Large-Scale Structure of the Universe, such as galaxies. In this review, we describe general solutions to the problems in the Big Bang cosmology carry out by a single scalar field. Then, with the use of current surveys, we show the constraints imposed on the inflationary parameters (ns; r), which allow us to make the connection between theoretical and observational cosmology. In this way, with the latest results, it is possible to select, or at least to constrain, the right inflationary model, parameterized by a single scalar field potential V (φ). Abstract El objetivo principal de este art´ıculoes ofrecer una introducci´oncualitativa a la teor´ıade la inflaci´onc´osmica y su relaci´oncon observaciones actuales. El modelo inflacionario resuelve algunos problemas fundamentales que desaf´ıanal modelo est´andarcosmol´ogico,denominado modelo del Big Bang caliente, como el problema de la Planicidad, el Horizonte y la inexistencia de Monopolos magn´eticos.Adicionalmente, provee una explicaci´onal origen de la estructura a gran escala del Universo, como son las galaxias.
    [Show full text]
  • Evolution of the Cosmological Horizons in a Concordance Universe
    Evolution of the Cosmological Horizons in a Concordance Universe Berta Margalef–Bentabol 1 Juan Margalef–Bentabol 2;3 Jordi Cepa 1;4 [email protected] [email protected] [email protected] 1Departamento de Astrofísica, Universidad de la Laguna, E-38205 La Laguna, Tenerife, Spain: 2Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, E-28040 Madrid, Spain. 3Facultad de Ciencias Físicas, Universidad Complutense de Madrid, E-28040 Madrid, Spain. 4Instituto de Astrofísica de Canarias, E-38205 La Laguna, Tenerife, Spain. Abstract The particle and event horizons are widely known and studied concepts, but the study of their properties, in particular their evolution, have only been done so far considering a single state equation in a deceler- ating universe. This paper is the first of two where we study this problem from a general point of view. Specifically, this paper is devoted to the study of the evolution of these cosmological horizons in an accel- erated universe with two state equations, cosmological constant and dust. We have obtained closed-form expressions for the horizons, which have allowed us to compute their velocities in terms of their respective recession velocities that generalize the previous results for one state equation only. With the equations of state considered, it is proved that both velocities remain always positive. Keywords: Physics of the early universe – Dark energy theory – Cosmological simulations This is an author-created, un-copyedited version of an article accepted for publication in Journal of Cosmology and Astroparticle Physics. IOP Publishing Ltd/SISSA Medialab srl is not responsible for any errors or omissions in this version of the manuscript or any version derived from it.
    [Show full text]
  • Or Causality Problem) the Flatness Problem (Or Fine Tuning Problem
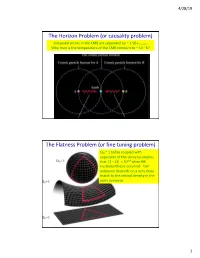
    4/28/19 The Horizon Problem (or causality problem) Antipodal points in the CMB are separated by ~ 1.96 rhorizon. Why then is the temperature of the CMB constant to ~ 10-5 K? The Flatness Problem (or fine tuning problem) W0 ~ 1 today coupled with expansion of the Universe implies that |1 – W| < 10-14 when BB nucleosynthesis occurred. Our existence depends on a very close match to the critical density in the early Universe 1 4/28/19 Theory of Cosmic Inflation Universe undergoes brief period of exponential expansion How Inflation Solves the Flatness Problem 2 4/28/19 Cosmic Inflation Summary Standard Big Bang theory has problems with tuning and causality Inflation (exponential expansion) solves these problems: - Causality solved by observable Universe having grown rapidly from a small region that was in causal contact before inflation - Fine tuning problems solved by the diluting effect of inflation Inflation naturally explains origin of large scale structure: - Early Universe has quantum fluctuations both in space-time itself and in the density of fields in space. Inflation expands these fluctuation in size, moving them out of causal contact with each other. Thus, large scale anisotropies are “frozen in” from which structure can form. Some kind of inflation appears to be required but the exact inflationary model not decided yet… 3 4/28/19 BAO: Baryonic Acoustic Oscillations Predict an overdensity in baryons (traced by galaxies) ~ 150 Mpc at the scale set by the distance that the baryon-photon acoustic wave could have traveled before CMB recombination 4 4/28/19 Curves are different models of Wm A measure of clustering of SDSS Galaxies of clustering A measure Eisenstein et al.
    [Show full text]
  • Phy306 Introduction to Cosmology Homework 3 Notes
    PHY306 INTRODUCTION TO COSMOLOGY HOMEWORK 3 NOTES 1. Show that, for a universe which is not flat, 1 − Ω 1 − Ω = , where Ω = Ω r + Ω m + Ω Λ and the subscript 0 refers to the present time. [2] This was generally quite well done, although rather lacking in explanation. You should really define the Ωs, and you need to explain that you divide the expression for t by that for t0. 2. Suppose that inflation takes place around 10 −35 s after the Big Bang. Assume the following simplified properties of the universe: ● it is matter dominated from the end of inflation to the present day; ● at the present day 0.9 ≤ Ω ≤ 1.1; ● the universe is currently 10 10 years old; ● inflation is driven by a cosmological constant. Using these assumptions, calculate the minimum amount of inflation needed to resolve the flatness problem, and hence determine the value of the cosmological constant required if the inflation period ends at t = 10 −34 s. [4] This was not well done at all, although it is not really a complicated calculation. I think the principal problem was that people simply did not think it through—not only do you not explain what you’re doing to the marker, you frequently don’t explain it to yourself! Some people therefore got hopelessly confused between the two time periods involved—the matter-dominated epoch from 10 −34 s to 10 10 years, and the inflationary period from 10 −35 to 10 −34 s. The most common error—in fact, considerably more common than the right answer—was simply assuming that during the post-inflationary epoch 1 − .
    [Show full text]
  • The High Redshift Universe: Galaxies and the Intergalactic Medium
    The High Redshift Universe: Galaxies and the Intergalactic Medium Koki Kakiichi M¨unchen2016 The High Redshift Universe: Galaxies and the Intergalactic Medium Koki Kakiichi Dissertation an der Fakult¨atf¨urPhysik der Ludwig{Maximilians{Universit¨at M¨unchen vorgelegt von Koki Kakiichi aus Komono, Mie, Japan M¨unchen, den 15 Juni 2016 Erstgutachter: Prof. Dr. Simon White Zweitgutachter: Prof. Dr. Jochen Weller Tag der m¨undlichen Pr¨ufung:Juli 2016 Contents Summary xiii 1 Extragalactic Astrophysics and Cosmology 1 1.1 Prologue . 1 1.2 Briefly Story about Reionization . 3 1.3 Foundation of Observational Cosmology . 3 1.4 Hierarchical Structure Formation . 5 1.5 Cosmological probes . 8 1.5.1 H0 measurement and the extragalactic distance scale . 8 1.5.2 Cosmic Microwave Background (CMB) . 10 1.5.3 Large-Scale Structure: galaxy surveys and Lyα forests . 11 1.6 Astrophysics of Galaxies and the IGM . 13 1.6.1 Physical processes in galaxies . 14 1.6.2 Physical processes in the IGM . 17 1.6.3 Radiation Hydrodynamics of Galaxies and the IGM . 20 1.7 Bridging theory and observations . 23 1.8 Observations of the High-Redshift Universe . 23 1.8.1 General demographics of galaxies . 23 1.8.2 Lyman-break galaxies, Lyα emitters, Lyα emitting galaxies . 26 1.8.3 Luminosity functions of LBGs and LAEs . 26 1.8.4 Lyα emission and absorption in LBGs: the physical state of high-z star forming galaxies . 27 1.8.5 Clustering properties of LBGs and LAEs: host dark matter haloes and galaxy environment . 30 1.8.6 Circum-/intergalactic gas environment of LBGs and LAEs .
    [Show full text]
  • Anisotropy of the Cosmic Background Radiation Implies the Violation Of
    YITP-97-3, gr-qc/9707043 Anisotropy of the Cosmic Background Radiation implies the Violation of the Strong Energy Condition in Bianchi type I Universe Takeshi Chiba, Shinji Mukohyama, and Takashi Nakamura Yukawa Institute for Theoretical Physics, Kyoto University, Kyoto 606-01, Japan (January 1, 2018) Abstract We consider the horizon problem in a homogeneous but anisotropic universe (Bianchi type I). We show that the problem cannot be solved if (1) the matter obeys the strong energy condition with the positive energy density and (2) the Einstein equations hold. The strong energy condition is violated during cosmological inflation. PACS numbers: 98.80.Hw arXiv:gr-qc/9707043v1 18 Jul 1997 Typeset using REVTEX 1 I. INTRODUCTION The discovery of the cosmic microwave background (CMB) [1] verified the hot big bang cosmology. The high degree of its isotropy [2], however, gave rise to the horizon problem: Why could causally disconnected regions be isotropized? The inflationary universe scenario [3] may solve the problem because inflation made it possible for the universe to expand enormously up to the presently observable scale in a very short time. However inflation is the sufficient condition even if the cosmic no hair conjecture [4] is proved. Here, a problem again arises: Is inflation the unique solution to the horizon problem? What is the general requirement for the solution of the horizon problem? Recently, Liddle showed that in FRW universe the horizon problem cannot be solved without violating the strong energy condition if gravity can be treated classically [5]. Actu- ally the strong energy condition is violated during inflation.
    [Show full text]
  • AST4220: Cosmology I
    AST4220: Cosmology I Øystein Elgarøy 2 Contents 1 Cosmological models 1 1.1 Special relativity: space and time as a unity . 1 1.2 Curvedspacetime......................... 3 1.3 Curved spaces: the surface of a sphere . 4 1.4 The Robertson-Walker line element . 6 1.5 Redshifts and cosmological distances . 9 1.5.1 Thecosmicredshift . 9 1.5.2 Properdistance. 11 1.5.3 The luminosity distance . 13 1.5.4 The angular diameter distance . 14 1.5.5 The comoving coordinate r ............... 15 1.6 TheFriedmannequations . 15 1.6.1 Timetomemorize! . 20 1.7 Equationsofstate ........................ 21 1.7.1 Dust: non-relativistic matter . 21 1.7.2 Radiation: relativistic matter . 22 1.8 The evolution of the energy density . 22 1.9 The cosmological constant . 24 1.10 Some classic cosmological models . 26 1.10.1 Spatially flat, dust- or radiation-only models . 27 1.10.2 Spatially flat, empty universe with a cosmological con- stant............................ 29 1.10.3 Open and closed dust models with no cosmological constant.......................... 31 1.10.4 Models with more than one component . 34 1.10.5 Models with matter and radiation . 35 1.10.6 TheflatΛCDMmodel. 37 1.10.7 Models with matter, curvature and a cosmological con- stant............................ 40 1.11Horizons.............................. 42 1.11.1 Theeventhorizon . 44 1.11.2 Theparticlehorizon . 45 1.11.3 Examples ......................... 46 I II CONTENTS 1.12 The Steady State model . 48 1.13 Some observable quantities and how to calculate them . 50 1.14 Closingcomments . 52 1.15Exercises ............................. 53 2 The early, hot universe 61 2.1 Radiation temperature in the early universe .
    [Show full text]
  • New Varying Speed of Light Theories
    New varying speed of light theories Jo˜ao Magueijo The Blackett Laboratory,Imperial College of Science, Technology and Medicine South Kensington, London SW7 2BZ, UK ABSTRACT We review recent work on the possibility of a varying speed of light (VSL). We start by discussing the physical meaning of a varying c, dispelling the myth that the constancy of c is a matter of logical consistency. We then summarize the main VSL mechanisms proposed so far: hard breaking of Lorentz invariance; bimetric theories (where the speeds of gravity and light are not the same); locally Lorentz invariant VSL theories; theories exhibiting a color dependent speed of light; varying c induced by extra dimensions (e.g. in the brane-world scenario); and field theories where VSL results from vacuum polarization or CPT violation. We show how VSL scenarios may solve the cosmological problems usually tackled by inflation, and also how they may produce a scale-invariant spectrum of Gaussian fluctuations, capable of explaining the WMAP data. We then review the connection between VSL and theories of quantum gravity, showing how “doubly special” relativity has emerged as a VSL effective model of quantum space-time, with observational implications for ultra high energy cosmic rays and gamma ray bursts. Some recent work on the physics of “black” holes and other compact objects in VSL theories is also described, highlighting phenomena associated with spatial (as opposed to temporal) variations in c. Finally we describe the observational status of the theory. The evidence is slim – redshift dependence in alpha, ultra high energy cosmic rays, and (to a much lesser extent) the acceleration of the universe and the WMAP data.
    [Show full text]
  • The Rh = Ct Universe Without Inflation
    A&A 553, A76 (2013) Astronomy DOI: 10.1051/0004-6361/201220447 & c ESO 2013 Astrophysics The Rh = ct universe without inflation F. Melia Department of Physics, The Applied Math Program, and Department of Astronomy, The University of Arizona, Tucson, AZ 85721, USA e-mail: [email protected] Received 26 September 2012 / Accepted 3 April 2013 ABSTRACT Context. The horizon problem in the standard model of cosmology (ΛDCM) arises from the observed uniformity of the cosmic microwave background radiation, which has the same temperature everywhere (except for tiny, stochastic fluctuations), even in regions on opposite sides of the sky, which appear to lie outside of each other’s causal horizon. Since no physical process propagating at or below lightspeed could have brought them into thermal equilibrium, it appears that the universe in its infancy required highly improbable initial conditions. Aims. In this paper, we demonstrate that the horizon problem only emerges for a subset of Friedmann-Robertson-Walker (FRW) cosmologies, such as ΛCDM, that include an early phase of rapid deceleration. Methods. The origin of the problem is examined by considering photon propagation through a FRW spacetime at a more fundamental level than has been attempted before. Results. We show that the horizon problem is nonexistent for the recently introduced Rh = ct universe, obviating the principal motivation for the inclusion of inflation. We demonstrate through direct calculation that, in this cosmology, even opposite sides of the cosmos have remained causally connected to us – and to each other – from the very first moments in the universe’s expansion. −35 −32 Therefore, within the context of the Rh = ct universe, the hypothesized inflationary epoch from t = 10 sto10 s was not needed to fix this particular “problem”, though it may still provide benefits to cosmology for other reasons.
    [Show full text]
  • A New Scale of Particle Mass in a Fractal Universe with A
    A new scale of particle mass in a fractal universe with a cosmological constant Scott Funkhouser(1) and Nicola Pugno(2) (1)Dept of Physics, the Citadel, 171 Moultrie St. Charleston, SC, 29409 (2)Department of Structural Engineering, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Torino, Italy ABSTRACT Considerations of the total action of a fractal universe with a cosmological constant lead to a new microscopic mass scale that is a function of the fractal dimension and fundamental parameters. For a universe with a fractal dimension D=2 the model predicts a mass that is of order near the nucleon mass. A scaling law between the cosmological constant and the mass of the nucleon follows that is identical to a known scaling law originating with Zel’dovich. This analysis also provides new limitations on the possible nature of dark matter in a fractal universe with a cosmological constant. 1. A new scale of mass Consider a system that is well represented by a fractal structure with dimension D. Let the total mass M of the system be dominated by some number N of a certain species of particle whose mass is m, so that N≈M/m. The total action A of the fractal system must be related to the Planck quantum of action h by [1,2] M ( D +1)/ D A ≈ hN (D +1)/ D ≈ h . (1) m Certain prominent features of the universe exhibit strong signatures of a fractal structure. Insomuch as the universe may be represented by a fractal, (1) should relate the total cosmic action to the parameters of the dominant species of massive particles in the universe [2].
    [Show full text]