DOCSLIB.ORG

Cosmic Microwave Background Anisotropies and Theories Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cosmic Microwave Background Anisotropies and Theories Of Cosmic Microwave Background Anisotropies and Theories of the Early Universe A dissertation submitted in satisfaction of the final requirement for the degree of Doctor Philosophiae SISSA – International School for Advanced Studies Astrophysics Sector arXiv:astro-ph/9512161v1 26 Dec 1995 Candidate: Supervisor: Alejandro Gangui Dennis W. Sciama October 1995 TO DENISE Abstract In this thesis I present recent work aimed at showing how currently competing theories of the early universe leave their imprint on the temperature anisotropies of the cosmic microwave background (CMB) radiation. After some preliminaries, where we review the current status of the field, we con- sider the three–point correlation function of the temperature anisotropies, as well as the inherent theoretical uncertainties associated with it, for which we derive explicit analytic formulae. These tools are of general validity and we apply them in the study of possible non–Gaussian features that may arise on large angular scales in the framework of both inflationary and topological defects models. In the case where we consider possible deviations of the CMB from Gaussian statis- tics within inflation, we develop a perturbative analysis for the study of spatial corre- lations in the inflaton field in the context of the stochastic approach to inflation. We also include an analysis of a particular geometry of the CMB three–point func- tion (the so–called ‘collapsed’ three–point function) in the case of post–recombination integrated effects, which arises generically whenever the mildly non–linear growth of perturbations is taken into account. We also devote a part of the thesis to the study of recently proposed analytic models for topological defects, and implement them in the analysis of both the CMB excess kurtosis (in the case of cosmic strings) and the CMB collapsed three–point function and skewness (in the case of textures). Lastly, we present a study of the CMB anisotropies on the degree angular scale in the framework of the global texture scenario, and show the relevant features that arise; among these, the Doppler peaks. i ii Contents Abstract i Acknowledgements vi Units and Conventions vii Introduction 1 1 Standard cosmology: Overview 5 1.1 Theexpandinguniverse .......................... 5 1.2 The Einstein field equations . 6 1.3 Thermal evolution and nucleosynthesis . .... 9 1.4 The CMB radiation and gravitational instability . ....... 11 1.5 The perturbation spectrum at horizon crossing . ...... 13 1.6 Drawbacksofthestandardmodel . 15 2 Theories of the early universe 19 2.1 Inflation ................................... 20 2.1.1 Theparadigm: somehistory . 21 2.1.2 Scalarfielddynamics . 22 2.1.3 Problemsinflationcansolve . 25 2.1.4 Generation of density perturbations . .. 27 2.1.5 Evolutionoffluctuations . 29 2.1.6 Anoverviewofmodels . 32 2.1.7 Stochasticapproachtoinflation . 38 2.2 Topologicaldefects ............................. 42 iii 2.2.1 Phase transitions and finite temperature field theory . ..... 45 2.2.2 TheKibblemechanism . 46 2.2.3 Asurveyoftopologicaldefects. 48 2.2.4 Local and global monopoles and domain walls . 50 2.2.5 Aredefectsinflatedaway? . 52 2.2.6 Cosmicstrings ........................... 53 2.2.7 Observational features from cosmic strings . .... 54 2.2.8 Globaltextures ........................... 55 2.2.9 Evolutionofglobaltextures . 57 3 CMB anisotropies 61 ∆T 3.1 Contributions to T ............................ 62 3.2 Suppressionofanisotropies. .. 67 ∆T 3.3 Adiabatic fluctuations as source of T .................. 68 3.4 Non–lineareffects.............................. 70 3.5 Overview................................... 70 4 CMB statistics 75 4.1 Dealing with spherical harmonics . .. 75 4.2 The CMB two–point correlation function . ... 77 4.3 The CMB three–point correlation function . .... 79 4.4 Predictions of a theory: ensemble averages . ..... 81 5 Primordial non–Gaussian features 83 5.1 Stochastic inflation and the statistics of the gravitational potential . 84 5.1.1 Theinflatonbispectrum . 85 5.1.2 The three–point function of the gravitational potential ..... 88 5.2 TheCMBangularbispectrum . 90 5.3 TheCMBskewness............................. 92 5.3.1 Worked examples: inflationary models . 93 5.3.2 On the correlation between n and the sign of the skewness . 95 5.4 The r.m.s. skewness of a Gaussian field . 105 5.5 Discussion .................................. 106 iv 6 Integrated effects 109 6.1 Introduction................................. 109 6.2 Contribution to the CMB three–point correlation function from the Rees–Sciamaeffect ............................. 111 6.3 The r.m.s. collapsed three–point function . ...... 115 6.4 Results for the COBE–DMRexperiment . 115 7 On the CMB kurtosis from cosmic strings 119 7.1 Introduction................................. 119 7.2 The four–point temperature correlation function . ........ 121 7.3 The r.m.s. excess kurtosis of a Gaussian field . ..... 127 7.4 Discussion .................................. 131 8 Analytic modeling of textures 133 8.1 Introduction................................. 133 8.2 Texture–spotstatistics . 136 8.3 Spotcorrelations .............................. 139 8.4 Textures and the three–point function . 139 8.5 Discussion .................................. 142 9 Global textures and the Doppler peaks 145 ∆T 9.1 Acoustic oscillations and T ........................ 146 9.2 Lineartheorypowerspectra . 147 9.3 Choosinginitialconditions . 150 9.4 Angular power spectrum from global textures . 152 9.5 Discussion .................................. 153 References 157 v Acknowledgements First and foremost I would like to thank my supervisor Dennis Sciama for his constant support and encouragement. He gave me complete freedom to chose the topics of my research as well as my collaborators, and he always followed my work with enthusiasm. I would also like to thank the whole group of astrophysics for creating a nice envi- ronment suited for pursuing my studies; among them I warmly thank Antonio Lanza for being always so kind and ready–to–help us in any respect. For the many interactions we had and specially for the fact that working with them was lots of fun, I want to express my acknowledgement to Ruth Durrer, Francesco Lucchin, Sabino Matarrese, Silvia Mollerach, Leandros Perivolaropoulos, and Mairi Sakellariadou. Our fruitful collaboration form the basis of much of the work presented here. My officemates, Mar Bastero, Marco Cavagli`a, Luciano Rezzolla, and Luca Zampieri + ‘Pigi’ Monaco also deserve some credits for helping me to improve on my italian and better appreciate the local caff`e, . and specially for putting up with me during our many hours together. I am also grateful to my colleagues in Buenos Aires for their encouragement to pursue graduate studies abroad, and for their being always in contact with me. Richard Stark patiently devoted many 5–minuteses to listen to my often direction- less questions, and also helped me sometimes as an online English grammar. I also thank the computer staff@sissa: Marina Picek, Luisa Urgias and Roberto Innocente for all their help during these years, and for making computers friendly to me. Finally, I want to express my gratitude to my wife, for all her love and patience; I am happy to dedicate this thesis to her. And last but not least, I would like to say thanks to our families and friends; they always kept close to us and helped us better enjoy our stay in Trieste. vi Units and Conventions In this thesis we are concerned with the study of specific predictions for the cosmic microwave background (CMB) anisotropies as given by different early universe models. Thus, discussions will span a wide variety of length scales, ranging from the Planck length, passing through the grand unification scale (e.g., when inflation is supposed to have occurred and cosmological phase transitions might have led to the existence of topological defects), up to the size of the universe as a whole (as is the case when probing horizon–size perturbation scales, e.g., from the COBE–DMR maps).1 As in any branch of physics, it so happens that the chosen units and conventions are almost always dictated by the problem at hand (whether we are considering the microphysics of a cosmic string or the characteristic thickness of the wake of accreted matter that the string leaves behind due to its motion). It is not hard to imagine then that also here disparate units come into the game. Astronomers will not always feel comfortable with those units employed by particle physicists, and vice versa, and so it is worthwhile to spend some words in order to fix notation. The so–called natural units, namelyh ¯ = c = kB = 1, will be employed, unless otherwise indicated.h ¯ is Planck’s constant divided by 2π, c is the speed of light, and kB is Boltzmann’s constant. Thus, all dimensions can be expressed in terms of one energy–unit which is usually chosen as GeV = 109eV, and so [Energy] = [Mass] = [Temperature] = [Length]−1 = [Time]−1 . Some conversion factors that will be useful in what follows are 1GeV =1.60 10−3 erg (Energy) × 1GeV =1.16 1013 K (Temperature) × 1GeV =1.78 10−24 g (Mass) × 1 GeV−1 = 1.97 10−14 cm (Length) × 1 GeV−1 = 6.58 10−25 sec (Time) × mP stands for the Planck mass, and associated quantities are given (both in natural 1COBE stands for COsmic Background Explorer satellite, and DMR is the Differential Microwave Radiometer on board. vii and cgs units) by m = 1.22 1019GeV = 2.18 10−5g, l = 8.2 10−20GeV−1 P × × P × =1.62 10−33cm, and t =5.39 10−44sec. In these units Newton’s constant is given × P × by G =6.67 10−8cm3g−1sec−2 = m−2. × P These fundamental units will be replaced by other, more suitable, ones when study- ing issues on large–scale structure formation. In that case it is better to employ astro- nomical units, which for historical reasons are based on solar system quantities. Thus, the parsec (the distance at which the Earth–Sun mean distance (1 a.u.) subtends one second of arc) is given by 1 pc = 3.26 light years. Of course, even this is much too small for describing the typical distances an astronomer has to deal with and thus many times distances are quoted in megaparsecs, 1 Mpc = 3.1 1024cm.
Load more

Recommended publications
  • University of California Santa Cruz Quantum
    UNIVERSITY OF CALIFORNIA SANTA CRUZ QUANTUM GRAVITY AND COSMOLOGY A dissertation submitted in partial satisfaction of the requirements for the degree of DOCTOR OF PHILOSOPHY in PHYSICS by Lorenzo Mannelli September 2005 The Dissertation of Lorenzo Mannelli is approved: Professor Tom Banks, Chair Professor Michael Dine Professor Anthony Aguirre Lisa C. Sloan Vice Provost and Dean of Graduate Studies °c 2005 Lorenzo Mannelli Contents List of Figures vi Abstract vii Dedication viii Acknowledgments ix I The Holographic Principle 1 1 Introduction 2 2 Entropy Bounds for Black Holes 6 2.1 Black Holes Thermodynamics ........................ 6 2.1.1 Area Theorem ............................ 7 2.1.2 No-hair Theorem ........................... 7 2.2 Bekenstein Entropy and the Generalized Second Law ........... 8 2.2.1 Hawking Radiation .......................... 10 2.2.2 Bekenstein Bound: Geroch Process . 12 2.2.3 Spherical Entropy Bound: Susskind Process . 12 2.2.4 Relation to the Bekenstein Bound . 13 3 Degrees of Freedom and Entropy 15 3.1 Degrees of Freedom .............................. 15 3.1.1 Fundamental System ......................... 16 3.2 Complexity According to Local Field Theory . 16 3.3 Complexity According to the Spherical Entropy Bound . 18 3.4 Why Local Field Theory Gives the Wrong Answer . 19 4 The Covariant Entropy Bound 20 4.1 Light-Sheets .................................. 20 iii 4.1.1 The Raychaudhuri Equation .................... 20 4.1.2 Orthogonal Null Hypersurfaces ................... 24 4.1.3 Light-sheet Selection ......................... 26 4.1.4 Light-sheet Termination ....................... 28 4.2 Entropy on a Light-Sheet .......................... 29 4.3 Formulation of the Covariant Entropy Bound . 30 5 Quantum Field Theory in Curved Spacetime 32 5.1 Scalar Field Quantization .........................
    [Show full text]
  • Black Hole Singularity Resolution Via the Modified Raychaudhuri
    Black hole singularity resolution via the modified Raychaudhuri equation in loop quantum gravity Keagan Blanchette,a Saurya Das,b Samantha Hergott,a Saeed Rastgoo,a aDepartment of Physics and Astronomy, York University 4700 Keele Street, Toronto, Ontario M3J 1P3 Canada bTheoretical Physics Group and Quantum Alberta, Department of Physics and Astronomy, University of Lethbridge, 4401 University Drive, Lethhbridge, Alberta T1K 3M4, Canada E-mail: [email protected], [email protected], [email protected], [email protected] Abstract: We derive loop quantum gravity corrections to the Raychaudhuri equation in the interior of a Schwarzschild black hole and near the classical singularity. We show that the resulting effective equation implies defocusing of geodesics due to the appearance of repulsive terms. This prevents the formation of conjugate points, renders the singularity theorems inapplicable, and leads to the resolution of the singularity for this spacetime. arXiv:2011.11815v3 [gr-qc] 21 Apr 2021 Contents 1 Introduction1 2 Interior of the Schwarzschild black hole3 3 Classical dynamics6 3.1 Classical Hamiltonian and equations of motion6 3.2 Classical Raychaudhuri equation 10 4 Effective dynamics and Raychaudhuri equation 11 4.1 ˚µ scheme 14 4.2 µ¯ scheme 17 4.3 µ¯0 scheme 19 5 Discussion and outlook 22 1 Introduction It is well known that General Relativity (GR) predicts that all reasonable spacetimes are singular, and therefore its own demise. While a similar situation in electrodynamics was resolved in quantum electrodynamics, quantum gravity has not been completely formulated yet. One of the primary challenges of candidate theories such as string theory and loop quantum gravity (LQG) is to find a way of resolving the singularities.
    [Show full text]
  • Arxiv:Hep-Ph/9912247V1 6 Dec 1999 MGNTV COSMOLOGY IMAGINATIVE Abstract
    IMAGINATIVE COSMOLOGY ROBERT H. BRANDENBERGER Physics Department, Brown University Providence, RI, 02912, USA AND JOAO˜ MAGUEIJO Theoretical Physics, The Blackett Laboratory, Imperial College Prince Consort Road, London SW7 2BZ, UK Abstract. We review1 a few off-the-beaten-track ideas in cosmology. They solve a variety of fundamental problems; also they are fun. We start with a description of non-singular dilaton cosmology. In these scenarios gravity is modified so that the Universe does not have a singular birth. We then present a variety of ideas mixing string theory and cosmology. These solve the cosmological problems usually solved by inflation, and furthermore shed light upon the issue of the number of dimensions of our Universe. We finally review several aspects of the varying speed of light theory. We show how the horizon, flatness, and cosmological constant problems may be solved in this scenario. We finally present a possible experimental test for a realization of this theory: a test in which the Supernovae results are to be combined with recent evidence for redshift dependence in the fine structure constant. arXiv:hep-ph/9912247v1 6 Dec 1999 1. Introduction In spite of their unprecedented success at providing causal theories for the origin of structure, our current models of the very early Universe, in partic- ular models of inflation and cosmic defect theories, leave several important issues unresolved and face crucial problems (see [1] for a more detailed dis- cussion). The purpose of this chapter is to present some imaginative and 1Brown preprint BROWN-HET-1198, invited lectures at the International School on Cosmology, Kish Island, Iran, Jan.
    [Show full text]
  • 8.962 General Relativity, Spring 2017 Massachusetts Institute of Technology Department of Physics
    8.962 General Relativity, Spring 2017 Massachusetts Institute of Technology Department of Physics Lectures by: Alan Guth Notes by: Andrew P. Turner May 26, 2017 1 Lecture 1 (Feb. 8, 2017) 1.1 Why general relativity? Why should we be interested in general relativity? (a) General relativity is the uniquely greatest triumph of analytic reasoning in all of science. Simultaneity is not well-defined in special relativity, and so Newton's laws of gravity become Ill-defined. Using only special relativity and the fact that Newton's theory of gravity works terrestrially, Einstein was able to produce what we now know as general relativity. (b) Understanding gravity has now become an important part of most considerations in funda- mental physics. Historically, it was easy to leave gravity out phenomenologically, because it is a factor of 1038 weaker than the other forces. If one tries to build a quantum field theory from general relativity, it fails to be renormalizable, unlike the quantum field theories for the other fundamental forces. Nowadays, gravity has become an integral part of attempts to extend the standard model. Gravity is also important in the field of cosmology, which became more prominent after the discovery of the cosmic microwave background, progress on calculations of big bang nucleosynthesis, and the introduction of inflationary cosmology. 1.2 Review of Special Relativity The basic assumption of special relativity is as follows: All laws of physics, including the statement that light travels at speed c, hold in any inertial coordinate system. Fur- thermore, any coordinate system that is moving at fixed velocity with respect to an inertial coordinate system is also inertial.
    [Show full text]
  • Raychaudhuri and Optical Equations for Null Geodesic Congruences With
    Raychaudhuri and optical equations for null geodesic congruences with torsion Simone Speziale1 1 Aix Marseille Univ., Univ. de Toulon, CNRS, CPT, UMR 7332, 13288 Marseille, France October 17, 2018 Abstract We study null geodesic congruences (NGCs) in the presence of spacetime torsion, recovering and extending results in the literature. Only the highest spin irreducible component of torsion gives a proper acceleration with respect to metric NGCs, but at the same time obstructs abreastness of the geodesics. This means that it is necessary to follow the evolution of the drift term in the optical equations, and not just shear, twist and expansion. We show how the optical equations depend on the non-Riemannian components of the curvature, and how they reduce to the metric ones when the highest spin component of torsion vanishes. Contents 1 Introduction 1 2 Metric null geodesic congruences and optical equations 3 2.1 Null geodesic congruences and kinematical quantities . ................. 3 2.2 Dynamics: Raychaudhuri and optical equations . ............. 6 3 Curvature, torsion and their irreducible components 8 4 Torsion-full null geodesic congruences 9 4.1 Kinematical quantities and the congruence’s geometry . ................ 11 arXiv:1808.00952v3 [gr-qc] 16 Oct 2018 5 Raychaudhuri equation with torsion 13 6 Optical equations with torsion 16 7 Comments and conclusions 18 A Newman-Penrose notation 19 1 Introduction Torsion plays an intriguing role in approaches to gravity where the connection is given an indepen- dent status with respect to the metric. This happens for instance in the first-order Palatini and in the Einstein-Cartan versions of general relativity (see [1, 2, 3] for reviews and references therein), and in more elaborated theories with extra gravitational degrees of freedom like the Poincar´egauge 1 theory of gravity, see e.g.
    [Show full text]
  • Lecture 17 : the Cosmic Microwave Background
    Let’s think about the early Universe… Lecture 17 : The Cosmic ! From Hubble’s observations, we know the Universe is Microwave Background expanding ! This can be understood theoretically in terms of solutions of GR equations !Discovery of the Cosmic Microwave ! Earlier in time, all the matter must have been Background (ch 14) squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! !The Hot Big Bang This week: read Chapter 12/14 in textbook 4/15/14 1 4/15/14 3 Let’s think about the early Universe… Let’s think about the early Universe… ! From Hubble’s observations, we know the Universe is ! From Hubble’s observations, we know the Universe is expanding expanding ! This can be understood theoretically in terms of solutions of ! This can be understood theoretically in terms of solutions of GR equations GR equations ! Earlier in time, all the matter must have been squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! ! What was the Universe like long, long ago? ! What were the original contents? ! What were the early conditions like? ! What physical processes occurred under those conditions? ! How did changes over time result in the contents and structure we see today? 4/15/14 2 4/15/14 4 The Poetic Version ! In a brilliant flash about fourteen billion years ago, time and matter were born in a single instant of creation.
    [Show full text]
  • Analog Raychaudhuri Equation in Mechanics [14]
    Analog Raychaudhuri equation in mechanics Rajendra Prasad Bhatt∗, Anushree Roy and Sayan Kar† Department of Physics, Indian Institute of Technology Kharagpur, 721 302, India Abstract Usually, in mechanics, we obtain the trajectory of a particle in a given force field by solving Newton’s second law with chosen initial conditions. In contrast, through our work here, we first demonstrate how one may analyse the behaviour of a suitably defined family of trajectories of a given mechanical system. Such an approach leads us to develop a mechanics analog following the well-known Raychaudhuri equation largely studied in Riemannian geometry and general relativity. The idea of geodesic focusing, which is more familiar to a relativist, appears to be analogous to the meeting of trajectories of a mechanical system within a finite time. Applying our general results to the case of simple pendula, we obtain relevant quantitative consequences. Thereafter, we set up and perform a straightforward experiment based on a system with two pendula. The experimental results on this system are found to tally well with our proposed theoretical model. In summary, the simple theory, as well as the related experiment, provides us with a way to understand the essence of a fairly involved concept in advanced physics from an elementary standpoint. arXiv:2105.04887v1 [gr-qc] 11 May 2021 ∗ Present Address: Inter-University Centre for Astronomy and Astrophysics, Post Bag 4, Ganeshkhind, Pune 411 007, India †Electronic address: [email protected], [email protected], [email protected] 1 I. INTRODUCTION Imagine two pendula of the same length hung from a common support.
    [Show full text]
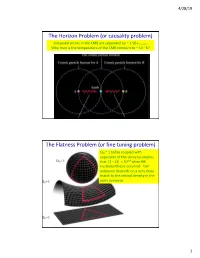
  • Or Causality Problem) the Flatness Problem (Or Fine Tuning Problem
    4/28/19 The Horizon Problem (or causality problem) Antipodal points in the CMB are separated by ~ 1.96 rhorizon. Why then is the temperature of the CMB constant to ~ 10-5 K? The Flatness Problem (or fine tuning problem) W0 ~ 1 today coupled with expansion of the Universe implies that |1 – W| < 10-14 when BB nucleosynthesis occurred. Our existence depends on a very close match to the critical density in the early Universe 1 4/28/19 Theory of Cosmic Inflation Universe undergoes brief period of exponential expansion How Inflation Solves the Flatness Problem 2 4/28/19 Cosmic Inflation Summary Standard Big Bang theory has problems with tuning and causality Inflation (exponential expansion) solves these problems: - Causality solved by observable Universe having grown rapidly from a small region that was in causal contact before inflation - Fine tuning problems solved by the diluting effect of inflation Inflation naturally explains origin of large scale structure: - Early Universe has quantum fluctuations both in space-time itself and in the density of fields in space. Inflation expands these fluctuation in size, moving them out of causal contact with each other. Thus, large scale anisotropies are “frozen in” from which structure can form. Some kind of inflation appears to be required but the exact inflationary model not decided yet… 3 4/28/19 BAO: Baryonic Acoustic Oscillations Predict an overdensity in baryons (traced by galaxies) ~ 150 Mpc at the scale set by the distance that the baryon-photon acoustic wave could have traveled before CMB recombination 4 4/28/19 Curves are different models of Wm A measure of clustering of SDSS Galaxies of clustering A measure Eisenstein et al.
    [Show full text]
  • Baryogenesis and Dark Matter from B Mesons: B-Mesogenesis
    Baryogenesis and Dark Matter from B Mesons: B-Mesogenesis Miguel Escudero Abenza [email protected] arXiv:1810.00880, PRD 99, 035031 (2019) with: Gilly Elor & Ann Nelson Based on: arXiv:2101.XXXXX with: Gonzalo Alonso-Álvarez & Gilly Elor New Trends in Dark Matter 09-12-2020 The Universe Baryonic Matter 5% 26% Dark Matter 69% Dark Energy Planck 2018 1807.06209 Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !2 Theoretical Understanding? Motivating Question: What fraction of the Energy Density of the Universe comes from Physics Beyond the Standard Model? 99.85%! Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !3 SM Prediction: Neutrinos 40% 60% Photons Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !4 The Universe Baryonic Matter 5% 26% Dark Matter 69% Dark Energy Planck 2018 1807.06209 Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !5 Baryogenesis and Dark Matter from B Mesons: B-Mesogenesis arXiv:1810.00880 Elor, Escudero & Nelson 1) Baryogenesis and Dark Matter are linked 2) Baryon asymmetry directly related to B-Meson observables 3) Leads to unique collider signatures 4) Fully testable at current collider experiments Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !6 Outline 1) B-Mesogenesis 1) C/CP violation 2) Out of equilibrium 3) Baryon number violation? 2) A Minimal Model & Cosmology 3) Implications for Collider Experiments 4) Dark Matter Phenomenology 5) Summary and Outlook Miguel Escudero (TUM) B-Mesogenesis New Trends in DM 09-12-20 !7 Baryogenesis
    [Show full text]
  • The Matter – Antimatter Asymmetry of the Universe and Baryogenesis
    The matter – antimatter asymmetry of the universe and baryogenesis Andrew Long Lecture for KICP Cosmology Class Feb 16, 2017 Baryogenesis Reviews in General • Kolb & Wolfram’s Baryon Number Genera.on in the Early Universe (1979) • Rio5o's Theories of Baryogenesis [hep-ph/9807454]} (emphasis on GUT-BG and EW-BG) • Rio5o & Trodden's Recent Progress in Baryogenesis [hep-ph/9901362] (touches on EWBG, GUTBG, and ADBG) • Dine & Kusenko The Origin of the Ma?er-An.ma?er Asymmetry [hep-ph/ 0303065] (emphasis on Affleck-Dine BG) • Cline's Baryogenesis [hep-ph/0609145] (emphasis on EW-BG; cartoons!) Leptogenesis Reviews • Buchmuller, Di Bari, & Plumacher’s Leptogenesis for PeDestrians, [hep-ph/ 0401240] • Buchmulcer, Peccei, & Yanagida's Leptogenesis as the Origin of Ma?er, [hep-ph/ 0502169] Electroweak Baryogenesis Reviews • Cohen, Kaplan, & Nelson's Progress in Electroweak Baryogenesis, [hep-ph/ 9302210] • Trodden's Electroweak Baryogenesis, [hep-ph/9803479] • Petropoulos's Baryogenesis at the Electroweak Phase Transi.on, [hep-ph/ 0304275] • Morrissey & Ramsey-Musolf Electroweak Baryogenesis, [hep-ph/1206.2942] • Konstandin's Quantum Transport anD Electroweak Baryogenesis, [hep-ph/ 1302.6713] Constituents of the Universe formaon of large scale structure (galaxy clusters) stars, planets, dust, people late ame accelerated expansion Image stolen from the Planck website What does “ordinary matter” refer to? Let’s break it down to elementary particles & compare number densities … electron equal, universe is neutral proton x10 billion 3⇣(3) 3 3 n =3 T 168 cm− neutron x7 ⌫ ⇥ 4⇡2 ⌫ ' matter neutrinos photon positron =0 2⇣(3) 3 3 n = T 413 cm− γ ⇡2 CMB ' anti-proton =0 3⇣(3) 3 3 anti-neutron =0 n =3 T 168 cm− ⌫¯ ⇥ 4⇡2 ⌫ ' anti-neutrinos antimatter What is antimatter? First predicted by Dirac (1928).
    [Show full text]
  • Baryogenesis and Dark Matter from B Mesons
    Baryogenesis and Dark Matter from B mesons Abstract: In [1] a new mechanism to simultaneously generate the baryon asymmetry of the Universe and the Dark Matter abundance has been proposed. The Standard Model of particle physics succeeds to describe many physical processes and it has been tested to a great accuracy. However, it fails to provide a Dark Matter candidate, a so far undetected component of matter which makes up roughly 25% of the energy budget of the Universe. Furthermore, the question arises why there is a more matter (or baryons) than antimatter in the Universe taking into account that cosmology predicts a Universe with equal parts matter and anti-matter. The mechanism to generate a primordial matter-antimatter asymmetry is called baryogenesis. Any successful mechanism for baryogenesis needs to satisfy the three Sakharov conditions [2]: • violation of charge symmetry and of the combination of charge and parity symmetry • violation of baryon number • departure from thermal equilibrium In this paper [1] a new mechanism for the generation of a baryon asymmetry together with Dark Matter production has been proposed. The mechanism proposed to explain the observed baryon asymetry as well as the pro- duction of dark matter is developed around a fundamental ingredient: a new scalar particle Φ. The Φ particle is massive and would dominate the energy density of the Universe after inflation but prior to the Bing Bang nucleosynthesis. The same particle will directly decay, out of thermal equilibrium, to b=¯b quarks and if the Universe is cool enough ∼ O(10 MeV), the produced b quarks can hadronize and form B-mesons.
    [Show full text]
  • Light Rays, Singularities, and All That
    Light Rays, Singularities, and All That Edward Witten School of Natural Sciences, Institute for Advanced Study Einstein Drive, Princeton, NJ 08540 USA Abstract This article is an introduction to causal properties of General Relativity. Topics include the Raychaudhuri equation, singularity theorems of Penrose and Hawking, the black hole area theorem, topological censorship, and the Gao-Wald theorem. The article is based on lectures at the 2018 summer program Prospects in Theoretical Physics at the Institute for Advanced Study, and also at the 2020 New Zealand Mathematical Research Institute summer school in Nelson, New Zealand. Contents 1 Introduction 3 2 Causal Paths 4 3 Globally Hyperbolic Spacetimes 11 3.1 Definition . 11 3.2 Some Properties of Globally Hyperbolic Spacetimes . 15 3.3 More On Compactness . 18 3.4 Cauchy Horizons . 21 3.5 Causality Conditions . 23 3.6 Maximal Extensions . 24 4 Geodesics and Focal Points 25 4.1 The Riemannian Case . 25 4.2 Lorentz Signature Analog . 28 4.3 Raychaudhuri’s Equation . 31 4.4 Hawking’s Big Bang Singularity Theorem . 35 5 Null Geodesics and Penrose’s Theorem 37 5.1 Promptness . 37 5.2 Promptness And Focal Points . 40 5.3 More On The Boundary Of The Future . 46 1 5.4 The Null Raychaudhuri Equation . 47 5.5 Trapped Surfaces . 52 5.6 Penrose’s Theorem . 54 6 Black Holes 58 6.1 Cosmic Censorship . 58 6.2 The Black Hole Region . 60 6.3 The Horizon And Its Generators . 63 7 Some Additional Topics 66 7.1 Topological Censorship . 67 7.2 The Averaged Null Energy Condition .
    [Show full text]