Pyroelectric Energy Harvesting: with Thermodynamic-Based Cycles
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Engineering Fundamentals of the Internal Combustion Engine
Engineering Fundamentals of the Internal Combustion Engine . I Willard W. Pulkrabek University of Wisconsin-· .. Platteville vi Contents 2-3 Mean Effective Pressure, 49 2-4 Torque and Power, 50 2-5 Dynamometers, 53 2-6 Air-Fuel Ratio and Fuel-Air Ratio, 55 2-7 Specific Fuel Consumption, 56 2-8 Engine Efficiencies, 59 2-9 Volumetric Efficiency, 60 , 2-10 Emissions, 62 2-11 Noise Abatement, 62 2-12 Conclusions-Working Equations, 63 Problems, 65 Design Problems, 67 3 ENGINE CYCLES 68 3-1 Air-Standard Cycles, 68 3-2 Otto Cycle, 72 3-3 Real Air-Fuel Engine Cycles, 81 3-4 SI Engine Cycle at Part Throttle, 83 3-5 Exhaust Process, 86 3-6 Diesel Cycle, 91 3-7 Dual Cycle, 94 3-8 Comparison of Otto, Diesel, and Dual Cycles, 97 3-9 Miller Cycle, 103 3-10 Comparison of Miller Cycle and Otto Cycle, 108 3-11 Two-Stroke Cycles, 109 3-12 Stirling Cycle, 111 3-13 Lenoir Cycle, 113 3-14 Summary, 115 Problems, 116 Design Problems, 120 4 THERMOCHEMISTRY AND FUELS 121 4-1 Thermochemistry, 121 4-2 Hydrocarbon Fuels-Gasoline, 131 4-3 Some Common Hydrocarbon Components, 134 4-4 Self-Ignition and Octane Number, 139 4-5 Diesel Fuel, 148 4-6 Alternate Fuels, 150 4-7 Conclusions, 162 Problems, 162 Design Problems, 165 Contents vii 5 AIR AND FUEL INDUCTION 166 5-1 Intake Manifold, 166 5-2 Volumetric Efficiency of SI Engines, 168 5-3 Intake Valves, 173 5-4 Fuel Injectors, 178 5-5 Carburetors, 181 5-6 Supercharging and Turbocharging, 190 5-7 Stratified Charge Engines and Dual Fuel Engines, 195 5-8 Intake for Two-Stroke Cycle Engines, 196 5-9 Intake for CI Engines, 199 -

Internal Combustion Engines Collection of Stationary
ASME International THE COOLSPRING POWER MUSEUM COLLECTION OF STATIONARY INTERNAL COMBUSTION ENGINES MECHANICAL ENGINEERING HERITAGE COLLECTION Coolspring Power Museum Coolspring, Pennsylvania June 16, 2001 The Coolspring Power Museu nternal combustion engines revolutionized the world I around the turn of th 20th century in much the same way that steam engines did a century before. One has only to imagine a coal-fired, steam-powered, air- plane to realize how important internal combustion was to the industrialized world. While the early gas engines were more expensive than the equivalent steam engines, they did not require a boiler and were cheap- er to operate. The Coolspring Power Museum collection documents the early history of the internal- combustion revolution. Almost all of the critical components of hundreds of innovations that 1897 Charter today’s engines have their ori- are no longer used). Some of Gas Engine gins in the period represented the engines represent real engi- by the collection (as well as neering progress; others are more the product of inventive minds avoiding previous patents; but all tell a story. There are few duplications in the collection and only a couple of manufacturers are represent- ed by more than one or two examples. The Coolspring Power Museum contains the largest collection of historically signifi- cant, early internal combustion engines in the country, if not the world. With the exception of a few items in the collection that 2 were driven by the engines, m Collection such as compressors, pumps, and generators, and a few steam and hot air engines shown for comparison purposes, the collection contains only internal combustion engines. -

Constant Volume Combustion: the Ultimate Gas Turbine Cycle
INFRASTRUCTURE MINING & METALS NUCLEAR, SECURITY & ENVIRONMENTAL OIL, GAS & CHEMICALS Constant volume combustion: the ultimate gas turbine cycle About Bechtel Bechtel is among the most respected engineering, project management, and construction companies in the world. We stand apart for our ability to get the job done right—no matter how big, how complex, or how remote. Bechtel operates through four global business units that specialize in infrastructure; mining and metals; nuclear, security and environmental; and oil, gas, and chemicals. Since its founding in 1898, Bechtel has worked on more than 25,000 projects in 160 countries on all seven continents. Today, our 58,000 colleagues team with customers, partners, and suppliers on diverse projects in nearly 40 countries. Guest Feature Also in this section Constant volume combustion: 00 DARPA-funded CVC projects the ultimate gas turbine cycle 00 Power cycle thermodynamics 00 History of CVC engineering By S. C. Gülen, PhD, PE; Principal Engineer, Bechtel Power Pulse detonation combustion holds the key to 45% simple cycle and close to 65% combined cycle efficiencies at today’s 1400-1500°C gas turbine firing temperatures. The Kelvin-Planck statement of the Second Law of Thermo- Why constant volume combustion? dynamics leaves no room for doubt: the maximum efficiency In a modern gas turbine with an approximately constant pres- of a heat engine operating in a thermodynamic cycle cannot sure combustor, the compressor section consumes close to exceed the efficiency of a Carnot cycle operating between 50% of gas turbine power output. the same hot and cold temperature reservoirs. Assume one could devise a combustion system where All practical heat engine cycles are attempts to approxi- energy added to the working fluid (i.e. -

Temperature Oscillations in the Wall of a Cooled Multi Pulsejet Propeller For
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Sheffield Hallam University Research Archive Temperature oscillations in the wall of a cooled multi pulsejet propeller for aeronautic propulsion TRANCOSSI, Michele, PASCOA, Jose and CARLOS, Xisto Available from Sheffield Hallam University Research Archive (SHURA) at: http://shura.shu.ac.uk/13964/ This document is the author deposited version. You are advised to consult the publisher's version if you wish to cite from it. Published version TRANCOSSI, Michele, PASCOA, Jose and CARLOS, Xisto (2016). Temperature oscillations in the wall of a cooled multi pulsejet propeller for aeronautic propulsion. SAE Technical Papers, 2016 (1-1998), 1-8. Repository use policy Copyright © and Moral Rights for the papers on this site are retained by the individual authors and/or other copyright owners. Users may download and/or print one copy of any article(s) in SHURA to facilitate their private study or for non- commercial research. You may not engage in further distribution of the material or use it for any profit-making activities or any commercial gain. Sheffield Hallam University Research Archive http://shura.shu.ac.uk Downloaded from SAE International by Michele Trancossi, Monday, November 07, 2016 Temperature Oscillations in the Wall of a Cooled Multi 2016-01-1998 Pulsejet Propeller for Aeronautic Propulsion Published 09/20/2016 Michele Trancossi Shefield Hallam University Jose Pascoa Universidade Da Beira Interior Carlos Xisto Chalmers University of Technology CITATION: Trancossi, M., Pascoa, J., and Xisto , C., "Temperature Oscillations in the Wall of a Cooled Multi Pulsejet Propeller for Aeronautic Propulsion," SAE Technical Paper 2016-01-1998, 2016, doi:10.4271/2016-01-1998. -

BASIC THERMODYNAMICS REFERENCES: ENGINEERING THERMODYNAMICS by P.K.NAG 3RD EDITION LAWS of THERMODYNAMICS
Module I BASIC THERMODYNAMICS REFERENCES: ENGINEERING THERMODYNAMICS by P.K.NAG 3RD EDITION LAWS OF THERMODYNAMICS • 0 th law – when a body A is in thermal equilibrium with a body B, and also separately with a body C, then B and C will be in thermal equilibrium with each other. • Significance- measurement of property called temperature. A B C Evacuated tube 100o C Steam point Thermometric property 50o C (physical characteristics of reference body that changes with temperature) – rise of mercury in the evacuated tube 0o C bulb Steam at P =1ice atm T= 30oC REASONS FOR NOT TAKING ICE POINT AND STEAM POINT AS REFERENCE TEMPERATURES • Ice melts fast so there is a difficulty in maintaining equilibrium between pure ice and air saturated water. Pure ice Air saturated water • Extreme sensitiveness of steam point with pressure TRIPLE POINT OF WATER AS NEW REFERENCE TEMPERATURE • State at which ice liquid water and water vapor co-exist in equilibrium and is an easily reproducible state. This point is arbitrarily assigned a value 273.16 K • i.e. T in K = 273.16 X / Xtriple point • X- is any thermomertic property like P,V,R,rise of mercury, thermo emf etc. OTHER TYPES OF THERMOMETERS AND THERMOMETRIC PROPERTIES • Constant volume gas thermometers- pressure of the gas • Constant pressure gas thermometers- volume of the gas • Electrical resistance thermometer- resistance of the wire • Thermocouple- thermo emf CELCIUS AND KELVIN(ABSOLUTE) SCALE H Thermometer 2 Ar T in oC N Pg 2 O2 gas -273 oC (0 K) Absolute pressure P This absolute 0K cannot be obtatined (Pg+Patm) since it violates third law. -

Thermodynamic Data
..................................APPENDIX A Thermodynamic data A.l Introduction The thermodynamic tables presented here for enthalpy and internal energy differ from those that are usually available, since they incorporate the enthalpy of formation. This means that there is no need for separate tabulations of calorific values, and it will be found that energy balances for combustion calculations are greatly simplified. The enthalpy of formation (t-.Hf) is perhaps more familiar to physical chemists than to engineers. The enthalpy of formation ( t-.Hf) of a substance is the standard reaction enthalpy for the formation of the compound from its elements in their reference state. The reference state of an element is its most stable state (for example, carbon atoms, but oxygen molecules) at a specified temperature and pressure, usually 298.15 K and a pressure of l bar. In the case of atoms that can exist in different forms, it is necessary to specify their form, for example, carbon is as graphite, not diamond. Combustion calculations are most readily undertaken by using absolute (some times known as sensible) internal energies or enthalpy. In steady-flow systems where there is displacement work then enthalpy should be used; this has been illustrated by figure 3.8. When there is no displacement work then internal energy should be used (figure 3.7). Consider now figure 3.8 in more detail. With an adiabatic combustion process from reactants (R) to products (P) the enthalpy is constant, but there is a substantial rise in temperature: (A.l) In the case of the isothermal combustion process (IR ~ IP) the temperature (T) is obviously constant, and the difference in enthalpy corresponds to the isobaric calorific value (-t-.Jfi,): t-.H~ = HR .T- HP,T (A.2) 582 Thermodynamic data A.2 Thermodynamic principles In the following sections, it will be seen how the thermodynamic data for internal energy, enthalpy, entropy and Gibbs function can all be determined from measurements of heat capacity and phase change enthalpies (or internal energies). -

Cranfield University Matthew Moxon Thermodynamic Analysis of The
Cranfield University Matthew Moxon Thermodynamic analysis of the Brayton-cycle gas- turbine under equilibrium chemistry assumptions School of Engineering PhD Academic year: 2010/2011 Supervisor: Professor Riti Singh July 2011 © Cranfield University, 2011. All rights reserved. No part of this publication may be reproduced without the written permission of the copyright holder. ii ABSTRACT A design-point thermodynamic model of the Brayton-cycle gas-turbine under assumptions of perfect chemical equilibrium is described. This approach is novel to the best knowledge of the author. The model uniquely derives an optimum work balance between power turbine and nozzle as a function of flight conditions and propulsor efficiency. The model may easily be expanded to allow analysis and comparison of arbitrary cycles using any combination of fuel and oxidizer. The model allows the consideration of engines under a variety of conditions, from sea level/static to >20 km altitude and flight Mach numbers greater than 4. Isentropic or polytropic turbomachinery component efficiency standards may be used independently for compressor, gas generator turbine and power turbine. With a methodology based on the paper by M.V. Casey, “Accounting for losses” (2007), and using Bridgman’s partial differentials , the model uniquely describes the properties of a gas turbine solely by reference to the properties of the gas mixture passing through the engine. Turbine cooling is modelled using a method put forward by Kurzke. Turboshaft, turboprop, separate exhaust turbofan and turbojet engines may be modelled. Where applicable, optimisation of the power turbine and exhaust nozzle work split for flight conditions and component performances is automatically undertaken. -
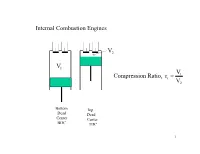
V V R Ratio, N Compressio = Internal Combustion Engines
Internal Combustion Engines V2 V1 V1 Compression Ratio, rc = V2 Bottom Top Dead Dead Center Center BDC TDC 1 Lenoir Cycle 1860 Intake Combustion Power TDC Exhaust TDC 0-1 1-2 2-3 3-0 p=constant v=constant Q=0 p=constant one revolution 2 Q Air Standard p v=c Q=0 Lenoir Cycle 0 3 1 Q p=c 2 v Air Standard Lenoir Cycle 2 Closed Thermodynamic System - quantity of mass Q q = Δu + w Q=0 p v=c 2 - 3 Combustion Process 0 v = constant Þ w = 0 3 q = u 2 - u1 1 Q p=c 2 - 3 Expansion Process, Power Stroke q = 0,adiabticprocess k k -1 k-1 T3 æ p3 ö æ v2 ö = ç ÷ = ç ÷ T2 è p2 ø è v1 ø w = -(u 2 - u3 ) 3-1 Exhaust Process p = c q = Δu + w q = (u1 - u3 ) + p3 (v1 - v3 ) = h1 - h3 w = q31 - (u3 - u1) 3 OTTO CYCLE , 2 Revolutions/cycle Compression Combustion Power Exhaust Exhaust Intake 1-2 2-3 3-4 4-1 1-0 0-1 TDC BDC TDC BDC revolution 1 revolution 2 3 p OTTO CYCLE spark ignition, SI fuel injection + SI 2 4 0 1 v 4 4 CYCLE, 2 REVOLUTIONS Revolution 1 Revolution 2 5 Air Standard Otto Cycle Closed System- a quantity of mass p p adiabatic and isentropic W Q v ignition exhaust opens W atmospheric pressure intake opens intake closes exhaust closes W v 6 AIR STANDARD OTTO CYCLE, 2 Revolutions/cycle Q in Qout V=c V=c W Win out Compression Combustion Expansion Exhaust 1-2 2-3 Power 4-1 3-4 p p Q adiabatic in W v=const isentropic 4 adiabatic 4 2 2 isentropic v=const Qout W 1 1 7 v v “COLD” Compression 1 ® 2, Δs = 0, pvk = c, q = 0, w = Δu k k Air Standard Otto Cycle p1v1 = p2v2 k-1 æ v ö ç 1 ÷ 3 T2 = T1ç ÷ è v2 ø Δs = 0 w 2-1 = Δu = u 2-u1 = cv (T2 - T1 ) T qin pvk = c Combustion 2 ® 3, v = c, w = pdv = 0, q =ΔU Q = 0, ò q2-3 = Δu = u3 - u 2 = cv (T3 - T2 ) 2 k 4 Expansion 3 ® 4, Δs = 0, pv = c, q = 0, w = ΔU k-1 q æ v ö out T = T ç 3 ÷ 4 3ç v ÷ 1 è 4 ø v w3-4 = Δu = u3 - u 4 = cv (T3 - T4 ) CLOSED SYSTEM Exhaust 4 ®1, v = c, w = ò pdv = 0, q =ΔU q = Δu + w q4-1 = Δu = u 4 - u1 = cv (T4 - T1 ) "COLD"Þ Cycle constant c c at T . -

Thermodynamics in Nuclear Power Plant Systems Bahman Zohuri • Patrick Mcdaniel
Thermodynamics in Nuclear Power Plant Systems Bahman Zohuri • Patrick McDaniel Thermodynamics in Nuclear Power Plant Systems Bahman Zohuri Patrick McDaniel Department of Nuclear Engineering Department of Chemical and Nuclear University of New Mexico Engineering Albuquerque University of New Mexico USA Albuquerque USA A solution manual for this book is available on Springer.com. ISBN 978-3-319-13418-5 ISBN 978-3-319-13419-2 (eBook) DOI 10.1007/978-3-319-13419-2 Library of Congress Control Number: 2015935571 Springer Cham Heidelberg New York Dordrecht London © Springer International Publishing Switzerland 2015 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. -

Thermodynamic Analysis and Preliminary Design of the Cooling
Thermodynamic analysis and preliminary design of the cooling system of a pulsejet for aeronautic propulsion TRANCOSSI, Michele, MOHAMMEDALAMIN, Omer, PASCOA, Jose and RODRIGUES, Frederico Available from Sheffield Hallam University Research Archive (SHURA) at: http://shura.shu.ac.uk/13960/ This document is the author deposited version. You are advised to consult the publisher's version if you wish to cite from it. Published version TRANCOSSI, Michele, MOHAMMEDALAMIN, Omer, PASCOA, Jose and RODRIGUES, Frederico (2016). Thermodynamic analysis and preliminary design of the cooling system of a pulsejet for aeronautic propulsion. International Journal of Heat and Technology, 34 (2), S528-S534. Copyright and re-use policy See http://shura.shu.ac.uk/information.html Sheffield Hallam University Research Archive http://shura.shu.ac.uk INTERNATIONAL JOURNAL OF A publication of IIETA HEAT AND TECHNOLOGY ISSN: 0392-8764 Vol. 34, Special Issue 2, October 2016, pp. S528-S534 DOI: https://doi.org/10.18280/ijht.34S247 Licensed under CC BY-NC 4.0 http://www.iieta.org/Journals/IJHT Thermodynamic Analysis and Preliminary Design of the Cooling System of a Pulsejet for Aeronautic Propulsion Michele Trancossi 1*, Omer Mohammedalamin 2, Jose C. Pascoa 3 and Frederico Rodrigues 3 1 Material and Engineering Research Insitute, ACES, Sheffield Hallam University, City Campus, Howard Street, Sheffield S1 1WB, UK, 2 Faculty of Arts, Computing, Engineering and Sciences, Sheffield Hallam University, City Campus, Howard Street, Sheffield S1 1WB, UK 3 Center for Mechanical and Aerospace Science and Technology, Universitade da Beira Interior, 6200-Covilhã, PT Email: [email protected] ABSTRACT This paper is a preliminary step through an effective redesign of valved pulsejet. -

Schaum's Solved Problems Series
SCHAUM'S SOLVED PROBLEMS SERIES 2000 SOLVED PROBLEMS IN MECHANICAL ENGINEERING THERMODYNAMICS by Peter E. LUey, Ph.D. Purdue Üniversity McGRAW-HIIX PUBLISHING COMPANY New York St. Louis San Francisco Auckland Bogota Caracas Hamburg Lisbon London Madrid Mexico Milan Montreal New Delhi Oklahoma City Paris San Juan Säo Paulo Singapore Sydney Tokyo Toronto CONTENTS Chapter 1 BASIC CONCEPTS Pressure / Volume / Temperature / Mass / Mass Flow Rate / Capacity / Velocity / Acceleration of Gravity / Work and Energy Chapter 2 THERMODYNAMIC PROPERTIES OF FLUIDS. IDEAL GASES Ideal Gas Processes / Real Fluid Processes / One- and Two-Phase Processes / Tabular Data Acquisition / Quality / Compressibility Factor / Cntical Point / Specific Heat at Constant Pressure / Enthalpy of Vaporization / Enthalpy of Fusion / Enthalpy of Sublimation / Entropy Change / Gas Constant (Pure Substances) / Gas Constant (Mixtures) / Steam Table Usage / Ideal Gas Equation / Tds Equations / Miscellaneous Chapter 3 FIRST AND SECOND LAWS OF THERMODYNAMICS FOR CLOSED SYSTEMS 64 First Law of Thermodynamics / ßoundary Work / Paddle-Wheel Work / Spring Work / Electrical Work / Joule's Law / Mixing / Heat and Work Reservoirs / Incompressible Materials / Second Law of Thermodynamics / Entropy Principle / Heat Conduction / Miscellaneous 98 Chapter 4 REAL FLUIDS . (11- H Generalized Compressibility Factor Charts / Critical Point / The Maxwell Relations / Ciausius-Clapeyron Equation / Joule-Thompson Coefficient / Derived Latent-Heat Equations / Generalized Thermodynamic Relations / Vina! -

Open Chaves Andrew Investigationofpulsejetgeometry.Pdf
THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF AEROSPACE ENGINEERING INVESTIGATION OF PULSEJET ENGINE GEOMETRY FOR MAXIMUM THRUST EFFICIENCY ANDREW DAVID CHAVES Spring 2012 A thesis submitted in partial fulfillment of the requirements for a baccalaureate degree in Aerospace Engineering with honors in Aerospace Engineering Reviewed and approved* by the following: Michael M. Micci Professor of Aerospace Engineering Thesis Supervisor Dennis K. McLaughlin Professor of Aerospace Engineering Honors Advisor George A. Lesieutre Head of Aerospace Engineering Professor of Aerospace Engineering * Signatures are on file in the Schreyer Honors College i Abstract Pulsejet technology, one of the simplest forms of propulsion known, has been around since the early 1900s. It got its first practical application in the 1930s on the German V-1 flying bomb, or “Buzz-Bomb.” Interest in pulsejet applications then subsided due to the continuing development and improvement of the turbojet engine. Recently though, there has been renewed interest in pulsejets as an alternative to chemical rocket propulsion. Advances in computational simulation and modeling now allow better modeling of the operation process. In this research, COMSOL Multiphysics is utilized to develop a computational model to simulate a pulsejet engine and the phenomena of its operation. Conservation of momentum, mass, and energy equations are solved for one-dimensional, unsteady, compressible flow. The simulation shows how compression and expansion (rarefaction) waves propagate