Portfolio Optimization of Wind Power Projects
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Nytt Regionråd I Namdalen
NYTT REGIONRÅD I NAMDALEN Namdal regionråd Forslag fra Region Namdal NOTAT Innholdsfortegnelse Forord ......................................................................................................................................................2 Mandat .....................................................................................................................................................2 Hovedmål for nytt regionråd .................................................................................................................3 Bakgrunnskapittel ..................................................................................................................................3 Oversikt over regionrådsoppgaver og MNS-oppgaver .................................................................................... 4 Oppgaver for nytt regionråd ..................................................................................................................4 1. Politisk samhandling i Namdalen .....................................................................................................4 2. Namdalstrategi .................................................................................................................................5 3. Høringer, uttalelser om regionale beslutninger/saker i Trøndelag, evt. nasjonalt ...........................5 4. Kommunale næringsfond .................................................................................................................6 5. Forvaltning av regionalt næringsfond -

Møteplan for Kommunestyrer Og Formannskap I Kommuner I Namdalen Høst 2018
Møteplan for kommunestyrer og formannskap i kommuner i Namdalen høst 2018 Uke Dato Mandag Dato Tirsdag Dato Onsdag Dato Torsdag Dato Fredag 36 03.09 04.09 Namsos FOR 05.09 Osen FOR 06.09 Namdalseid FOR 07.09 Røyrvik FOR Overhalla FOR Lierne KOM 37 10.09 Nærøy FOR 11.09 Grong FOR 12.09 Fosnes FOR 13.09 Flatanger KOM 14.09 Lierne FOR Namdalseid FOR Røyrvik KOM Høylandet FOR Grong KOM 38 17.09 Høylandet KOM 18.09 Flatanger FOR 19.09 Osen KOM 20.09 Vikna KOM 21.09 Nærøy KOM Namsos FOR Leka FOR Namsskogan KOM Vikna FOR Overhalla KOM 39 24.09 25.09 26.09 27.09 Namsos KOM 28.09 Fosnes KOM Leka KOM 40 01.10 02.10 Namsos FOR 03.10 Røyrvik FOR 04.10 Namdalseid FOR 05.10 Namsskogan FOR (Fosnes FOR) Overhalla FOR Lierne FOR 41 08.10 09.10 10.10 Nærøy FOR 11.10 12.10 (Fosnes FOR) 42 15.10 16.10 Namsos FOR 17.10 18.10 Høylandet FOR 19.10 Namsskogan KOM Grong FOR Osen FOR Vikna FOR 43 22.10 Overhalla KOM 23.10 Flatanger FOR 24.10 Osen KOM 25.10 Namdalseid FOR 26.10 Røyrvik KOM Leka FOR Namsos KOM Lierne FOR Fosnes KOM Høylandet KOM Grong KOM Vikna KOM 44 29.10 30.10 Namsos FOR 31.10 Leka KOM 01.11 Flatanger KOM 02.11 Namsskogan FOR Namdalseid KOM Lierne FOR Høylandet FOR 45 05.11 06.11 Overhalla FOR 07.11 Nærøy FOR 08.11 09.11 Lierne FOR Osen FOR Leka FOR Røyrvik FOR 46 12.11 13.11 Flatanger FOR 14.11 Fosnes FOR 15.11 16.11 Nærøy KOM Namsos FOR Høylandet FOR Namsskogan KOM Vikna FOR 47 19.11 20.11 Vikna KOM 21.11 Osen KOM 22.11 Høylandet KOM 23.11 Overhalla KOM Leka FOR Vikna FOR Lierne FOR Røyrvik KOM 48 26.11 27.11 Namsos FOR 28.11 Fosnes FOR 29.11 Namsos KOM 30.11 Nærøy FOR Fosnes KOM Namsskogan FOR Høylandet KOM Grong FOR Grong KOM Leka KOM Lierne KOM 49 03.12 Overhalla FOR 04.12 Flatanger FOR 05.12 Osen FOR 06.12 Høylandet FOR 07.12 Røyrvik FOR 50 10.12 Lierne FOR 11.12 Namsos FOR 12.12 13.12 Namdalseid KOM 14.12 Høylandet KOM Namsskogan KOM Namsos KOM Fosnes KOM Grong FOR Vikna KOM 51 17.12 Vikna FOR 18.12 Nærøy KOM 19.12 Osen KOM 20.12 Flatanger KOM 21.12 Overhalla KOM Grong KOM Røyrvik KOM KOM: Kommunestyremøte FOR: Formannskapsmøte . -

10Th European Heathland Workshop, Norway, 24Th of June – 1St of July 2007
1010thth EuropeanEuropean HeathlandHeathland WorkshopWorkshop 24th June - 1st July 2007, Central to Northern Norway Workshop,WWorkshop,Woorrkksshhoopp,, EExcursionEExcursionxxccuurrssiioonn aandaandnndd SSymposiumSSymposiumyymmppoossiiuumm GGuidesGGuidesuuiiddeess IngerIIngerInnggeerr E.EE.E.. MårenMMårenMåårreenn andaandanndd LivLLivLiivv S.SS.S.. NilsenNNilsenNiillsseenn (editors)((editors)(eeddiittoorrss)) DepartmentDDepartmentDeeppaarrttmmeenntt ofoofoff NaturalNNaturalNaattuurraall HistoryHHistoryHiissttoorryy && DDepartmentDDepartmenteeppaarrttmmeenntt ofoofoff BiologyBBiologyBiioollooggyy UniversityUUniversityUnniivveerrssiittyy oofoofff BBergenBBergeneerrggeenn Måren, I.E. & Nilsen L.S. (eds.) 2007. Threats, management and conservation of heathlands. Workshop, Excursion & Symposium Guides. 10th European Heathland Workshop, Norway, 24th of June – 1st of July 2007. Department of Natural History, Bergen Museum, & Department of Biology, University of Bergen Norway. Bergen, June 2007 Authors: Inger E. Måren and Liv S. Nilsen Design: Beate Helle Front page pictures: Giske L. Andersen & Inger E. Måren Printed copies: 150 © 2007 Department of Natural History at Bergen Museum & Department of Biology, University of Bergen, Norway Department of Natural History, Bergen Museum, University of Bergen Pb 7800 N-5020 Bergen, Norway E-mail: [email protected] Website: http://www.heathlands2007.uib.no/ Tel: +47 55 58 33 45 Fax: +47 55 58 96 67 Sponsored by: University of Bergen Torstein Erbos gavefond Directorate for Nature Management Norwegian Institute -

The Surveillance Programme for Pancreas Disease (PD) in 2017
Annual Report The surveillance programme for pancreas disease (PD) in 2017 Norwegian Veterinary Institute NORWEGIAN VETERINARY INSTITUTE The surveillance programme for pancreas disease (PD) in 2017 Content Summary ...................................................................................................................... 3 Introduction .................................................................................................................. 3 Aims ........................................................................................................................... 3 Materials and methods ..................................................................................................... 3 Results and Discussion ...................................................................................................... 4 References ................................................................................................................... 5 Authors Commissioned by Britt Bang Jensen, Anne-Gerd Gjevre ISSN 1894-5678 Design Cover: Reine Linjer © Norwegian Veterinary Institute 2018 Photo front page: Erling Svendsen Surveillance programmes in Norway – PD – Annual Report 2017 2 NORWEGIAN VETERINARY INSTITUTE Summary Salmonid alphavirus (SAV), the etiological agent of pancreas disease (PD), was detected in three farms in Nordland and one farm in Nord-Trøndelag during the surveillance programme in January to August 2017. After the enforcement of a new regulation, all farms will be tested for SAV, and SAV was thus detected -

Angeln an Der Küste Von Trøndelag Ein Angelparadies Mitten in Norwegen
ANGELN AN DER KÜSTE VON TRØNDELAG EIN ANGELPARADIES MITTEN IN NORWEGEN IHR ANGELFÜHRER WILLKOMMEN ZU HERRLICHEN ANGELERLEBNISSEN AN DER KÜSTE VON TRØNDELAG!! In Trøndelag sind alle Voraussetzungen für gute Angelerlebnisse vorhanden. Die Mischung aus einem Schärengarten voller Inseln, den geschützten Fjorden und dem leicht erreichbarem offenen Meer bietet für alle Hobbyangler ideale Verhältnisse, ganz entsprechend ihren persönlichen Erwartungen und Erfahrungen. An der gesamten Küste findet man gute Anlagen vor, deren Betreiber für Unterkunft, Boote, Ratschläge für die Sicherheit auf dem Wasser und natürlich Tipps zum Auffinden der besten Angelplätze sorgen. Diese Broschüre soll allen, die zum Angeln nach Trøndelag kommen, die Teilnahme an schönen Angelerlebnisse erleichtern. Im hinteren Teil finden Sie Hinweise für die Wahl der Ausrüstung, 02 zur Sicherheit im Boot und zu den gesetzlichen Bestimmungen. Außerdem präsentieren sich die verschiedenen Küstenregionen mit ihrer reichen Küstenkultur, die prägend für die Küste von Trøndelag ist. PHOTO: YNGVE ASK INHALT 02 Willkommen zu guten Angelmöglichkeiten in Trøndelag 04 Fischarten 07 Angelausrüstung und Tipps 08 Gesetzliche Bestimmungen für das Angeln im Meer 09 Angeln und Sicherheit 10 Fischrezepte 11 Hitra & Frøya 14 Fosen 18 Trondheimfjord 20 Namdalsküste 25 Betriebe 03 30 Karte PHOTO: TERJE RAKKE NORDIC LIFE NORDIC RAKKE TERJE PHOTO: FISCHARTEN vielen rötlichen Flecken. Sie kommt zahlreich HEILBUTT Seeteufel in der Nordsee in bis zu 250 m Tiefe vor. LUMB Der Lumb ist durch seine lange Rückenflosse Ein großer Kopf und ein riesiges Maul sind die gekennzeichnet. Normalerweise wiegt er um Kennzeichen dieser Art. Der Kopf macht fast die 3 kg, kann aber bis zu 20 kg erreichen. die halbe Körperlänge aus, die zwei Meter Man findet ihn oft in tiefen Fjorden, am Der Heilbutt ist der größte Plattfisch. -

AMFI Steinkjer Thon Eiendom - AMFI Steinkjer AMFI Steinkjer
1 567 mill OMSETNING (2020) 2 205 557 BESØKENDE (2020) 81 ANTALL BUTIKKER 39 161m² BUTIKKAREAL AMFI Steinkjer Thon Eiendom - AMFI Steinkjer AMFI Steinkjer AMFI Steinkjer er det største senteret nord i Trøndelag, og er inne i en god utvikling omsetningsmessig. - 2 - Thon Eiendom - AMFI Steinkjer OM SENTERET AMFI Steinkjer ligger i Trøndelag, midt i Steinkjer by. Senteret ligger tett inntil E6 og bare 5 minutters gange fra buss- og jernbanestasjon. Steinkjer ligger ca. 70 minutter fra Trondheim Lufthavn Værnes. Besøk senterets nettside på amfi.no/kjopesentre/amfi-steinkjer/ AMFI Steinkjer ønsker å være hjertet i lokalsamfunnet som samler lokalbefolkningen til inspirasjon, handel, fellesskap og glede. - 3 - Thon Eiendom - AMFI Steinkjer MARKED/KUNDEGRUNNLAG AMFI Steinkjer er et senter for alle, et familiesenter i Steinkjer sentrum. Primærmarked: Steinkjer/Inderøy/Verran, Snåsa/Namdalseid. Sekundærmarked: Verdal/Levanger, Namsos/Grong/Vikna og Fosen/Ørlandet. 2. Åfjord (4,279) 1. Steinkjer-Verran 2. Ørland (10,337) (24,240) 2. Namsos (15,130) 1. Nærøysund (9,649) 1. Indre Fosen (10,037) 2. Levanger (20,160) 1. Inderøy (6,802) 2. Verdal (14,989) 1. Snåsa (2,060) - 4 - Thon Eiendom - AMFI Steinkjer OMSETNING AMFI Steinkjer hadde i 2020 en omsetning på 1 567 millioner kroner, en økning på 5,4% fra 2019. Omsetningsutvikling År Omsetning Endring 2012 1 247 598 484 10% 2013 1 364 848 171 9% 2014 1 401 784 834 3% 2015 1 377 679 159 -2% 2016 1 451 328 384 5% 2017 1 437 845 740 -1% 2018 1 446 592 453 1% 2019 1 478 079 505 2,2% 2020 1 566 869 911 5,4% - 5 - Thon Eiendom - AMFI Steinkjer Kommentar til diagrammet: Senteret utvikles kontinuerlig for å kunne gi kundene en god handleopplevelse. -

Møteinnkalling
Møteinnkalling Utvalg: Fellesnemnda Indre Fosen kommune Møtested: Leksvik kommunehus, Kommunestyresalen Møtedato: 26.05.2016 Tid: 12:00 Forfall meldes til Servicekontorene som sørger for innkalling av varamedlemmer. Varamedlemmer møter kun ved spesiell innkalling. Innkalling er sendt til: Navn Funksjon Representerer Steinar Saghaug Leder LE-H Bjørnar Buhaug Medlem LE-SP Ove Vollan Ordfører RI-HØ Camilla Sollie Finsmyr Medlem LE-SP Liv Darell Medlem RI-SP Linda Renate Lutdal Medlem LE-H Bjørn Vangen Medlem RI-HØ Per Kristian Skjærvik Medlem RI-AP Knut Ola Vang Medlem LE-AP Torun Skjærvø Bakken Medlem RI-AP Merethe Kopreitan Dahl Medlem LE-AP Sigurd Saue Medlem LE-SV Line Marie Rosvold Abel Medlem LE-V Marthe Helen Småvik Medlem RI-FRP Harald Fagervold Medlem RI-PP Jon Normann Tviberg Medlem LE-KRF Vegard Heide Medlem RI-MDG Kurt Håvard Myrabakk Medlem LE-FRP Per Brovold Medlem RI-SV Odd - Arne Sakseid Medlem RI-KRF Stefan Hansen Medlem RI-V Drøftingssak: - Mulighetskommunen Indre Fosen. Innledning v/ Sissel Blix Aaknes og Kine Larsen Kimo i arbeidsgruppa for omdømmeprosjektet Orienteringssaker: - Planstrategi v/ plansjef Siri Vannebo og arealplanlegger Antonios Bruheim Markakis. - Omstillingsprogram for nærings- og arbeidsliv Indre Fosen kommune v/ prosjektleder Torun Skjærvø Bakken - Rapportering prosjektbudsjett v/ prosjektleder Vigdis Bolås - Rapportering arbeidsgruppene v/ ledere politiske arbeidsgrupper og prosjektleder -1- Info prosjektleder Info leder og nestleder i fellesnemnda Steinar Saghaug Ove Vollan Leder fellesnemnda Nestleder -

Nye Fylkes- Og Kommunenummer - Trøndelag Fylke Stortinget Vedtok 8
Ifølge liste Deres ref Vår ref Dato 15/782-50 30.09.2016 Nye fylkes- og kommunenummer - Trøndelag fylke Stortinget vedtok 8. juni 2016 sammenslåing av Nord-Trøndelag fylke og Sør-Trøndelag fylke til Trøndelag fylke fra 1. januar 2018. Vedtaket ble fattet ved behandling av Prop. 130 LS (2015-2016) om sammenslåing av Nord-Trøndelag og Sør-Trøndelag fylker til Trøndelag fylke og endring i lov om forandring av rikets inddelingsnavn, jf. Innst. 360 S (2015-2016). Sammenslåing av fylker gjør det nødvendig å endre kommunenummer i det nye fylket, da de to første sifrene i et kommunenummer viser til fylke. Statistisk sentralbyrå (SSB) har foreslått nytt fylkesnummer for Trøndelag og nye kommunenummer for kommunene i Trøndelag som følge av fylkessammenslåingen. SSB ble bedt om å legge opp til en trygg og fremtidsrettet organisering av fylkesnummer og kommunenummer, samt å se hen til det pågående arbeidet med å legge til rette for om lag ti regioner. I dag ble det i statsråd fastsatt forskrift om nærmere regler ved sammenslåing av Nord- Trøndelag fylke og Sør-Trøndelag fylke til Trøndelag fylke. Kommunal- og moderniseringsdepartementet fastsetter samtidig at Trøndelag fylke får fylkesnummer 50. Det er tidligere vedtatt sammenslåing av Rissa og Leksvik kommuner til Indre Fosen fra 1. januar 2018. Departementet fastsetter i tråd med forslag fra SSB at Indre Fosen får kommunenummer 5054. For de øvrige kommunene i nye Trøndelag fastslår departementet, i tråd med forslaget fra SSB, følgende nye kommunenummer: Postadresse Kontoradresse Telefon* Kommunalavdelingen Saksbehandler Postboks 8112 Dep Akersg. 59 22 24 90 90 Stein Ove Pettersen NO-0032 Oslo Org no. -

Viknakalenderen 2003
VII(NA-KALENDEREN 2 OO3 Karstenoen, Namdalen Iokr! r| sh rlrla,.r(crobg,i.cr ^rs .E I 1*1 -\.'-\^4 råi] I]RYI-I,TJP PÅ \1K\,\ ALDERSH I] I NI I9?.I P.rn,s lc.nxrtlStrnd I 07 05 lS3R h.ldd r dr \ni hnrL l.vl{ P.tr]tr. or'\hd I 15.0j.1910 Dc Cii.l se! aldcrshc orcn don:l lrn0ri lt)71 Januar 1 1 2. 3 4 5 2 6 7 8 9 1 0n 1 1 1 2 3 1 3 1 4 1 5 1 6 1 7 1 8" 1 I 4 20 2 1 22 23 24 25n 26 5 27 28 2 30 3 1 JEGERIN FRA YTRE - cs. 1930 I VIK\Å Alsel HeU€sø med Evcakinn og bøm. Han var en meset dyktig jeser, os det er vel m på Vikna son hd skuft så mye rcv. oter os kobbc son nenop Atsel bodde på Bø6øya. Ha. ble lødt l?.06.1900. ALFRED PÅ KRÅKøYA-c!. I'?3 AlfEdAnde^eni lbinscnsin Hanblefødti l89SosvarsinmedAslaugAunet. Februar 5 1' 2 o 3 4 5 6 7 I 9" 7 1 0 1 1 1 2 1 3 1 4 1 5 16 I 1 7" 1 8 1 9 20 21 22 23n I 24 25 26 27 28 MOR OG DATTER - I9O5 Magdal€hc Hagen, t I 8 s 3, poseier samnen ned Magdal€ne var sin med Ole Lasen Hagø.. ) ''Rakcl varbysdlomscrlskoyt.6rliskcrvColiDArchcr,Lrrukl896.Bålenharhannereciereoppsjcnndmårenc.osil9lzkjøprcbrodrcDcK,lrc lirdot. Nordhrv' var bygd so'n norgdll og rilhønc Hclec Bondd Cavlen ble bygd hos Rudoll Sorli i OllcAø] i 19,15 ncd er ,45llK Rapprnotor ''Nordhav larrisnnok cn !v dc sroFrc no{gr!lcne i Midt Norge pi d€n riden. -
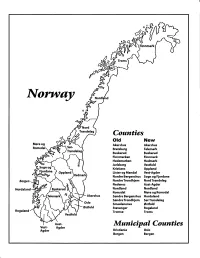
Norway Maps.Pdf
Finnmark lVorwny Trondelag Counties old New Akershus Akershus Bratsberg Telemark Buskerud Buskerud Finnmarken Finnmark Hedemarken Hedmark Jarlsberg Vestfold Kristians Oppland Oppland Lister og Mandal Vest-Agder Nordre Bergenshus Sogn og Fjordane NordreTrondhjem NordTrondelag Nedenes Aust-Agder Nordland Nordland Romsdal Mgre og Romsdal Akershus Sgndre Bergenshus Hordaland SsndreTrondhjem SorTrondelag Oslo Smaalenenes Ostfold Ostfold Stavanger Rogaland Rogaland Tromso Troms Vestfold Aust- Municipal Counties Vest- Agder Agder Kristiania Oslo Bergen Bergen A Feiring ((r Hurdal /\Langset /, \ Alc,ersltus Eidsvoll og Oslo Bjorke \ \\ r- -// Nannestad Heni ,Gi'erdrum Lilliestrom {", {udenes\ ,/\ Aurpkog )Y' ,\ I :' 'lv- '/t:ri \r*r/ t *) I ,I odfltisard l,t Enebakk Nordbv { Frog ) L-[--h il 6- As xrarctaa bak I { ':-\ I Vestby Hvitsten 'ca{a", 'l 4 ,- Holen :\saner Aust-Agder Valle 6rrl-1\ r--- Hylestad l- Austad 7/ Sandes - ,t'r ,'-' aa Gjovdal -.\. '\.-- ! Tovdal ,V-u-/ Vegarshei I *r""i'9^ _t Amli Risor -Ytre ,/ Ssndel Holt vtdestran \ -'ar^/Froland lveland ffi Bergen E- o;l'.t r 'aa*rrra- I t T ]***,,.\ I BYFJORDEN srl ffitt\ --- I 9r Mulen €'r A I t \ t Krohnengen Nordnest Fjellet \ XfC KORSKIRKEN t Nostet "r. I igvono i Leitet I Dokken DOMKIRKEN Dar;sird\ W \ - cyu8npris Lappen LAKSEVAG 'I Uran ,t' \ r-r -,4egry,*T-* \ ilJ]' *.,, Legdene ,rrf\t llruoAs \ o Kirstianborg ,'t? FYLLINGSDALEN {lil};h;h';ltft t)\l/ I t ,a o ff ui Mannasverkl , I t I t /_l-, Fjosanger I ,r-tJ 1r,7" N.fl.nd I r\a ,, , i, I, ,- Buslr,rrud I I N-(f i t\torbo \) l,/ Nes l-t' I J Viker -- l^ -- ---{a - tc')rt"- i Vtre Adal -o-r Uvdal ) Hgnefoss Y':TTS Tryistr-and Sigdal Veggli oJ Rollag ,y Lvnqdal J .--l/Tranbv *\, Frogn6r.tr Flesberg ; \. -

Poststeder Nord-Trøndelag Listet Alfabetisk Med Henvisning Til Kommune
POSTSTEDER NORD-TRØNDELAG LISTET ALFABETISK MED HENVISNING TIL KOMMUNE Aabogen i Foldereid ......................... Nærøy Einviken ..................................... Flatanger Aadalen i Forradalen ...................... Stjørdal Ekne .......................................... Levanger Aarfor ............................................ Nærøy Elda ........................................ Namdalseid Aasen ........................................ Levanger Elden ...................................... Namdalseid Aasenfjorden .............................. Levanger Elnan ......................................... Steinkjer Abelvær ......................................... Nærøy Elnes .............................................. Verdal Agle ................................................ Snåsa Elvalandet .................................... Namsos Alhusstrand .................................. Namsos Elvarli .......................................... Stjørdal Alstadhoug i Schognen ................. Levanger Elverlien ....................................... Stjørdal Alstadhoug ................................. Levanger Faksdal ......................................... Fosnes Appelvær........................................ Nærøy Feltpostkontor no. III ........................ Vikna Asp ............................................. Steinkjer Feltpostkontor no. III ................... Levanger Asphaugen .................................. Steinkjer Finnanger ..................................... Namsos Aunet i Leksvik .............................. -

Midtre Gauldal Kommune
Kartlegging av radon i Midtre Gauldal kommune Radon 2000/2001 Vinteren 2000/2001 ble det gjennomført en fase 1-kartlegging av radon i inneluft i Midtre Gauldal kommune, i forbindelse med den landsomfattende undersøkelsen ”Radon 2000/2001”. En andel på 8 % av kommunens husstander deltok i kartleggingen, og det ble funnet at 8 % av disse har en radonkonsentrasjon som er høyere enn anbefalt tiltaksnivå på 200 Bq/m3 luft. Midtre Gauldal kommune har et stedvis radonproblem, og kommunen kan deles inn i ulike områder med tanke på oppfølging. På Klokkerhaugen og Singsås er flere enn 20 % av målingene over tiltaksgrensen på 200 Bq/m3 radon i luft, og det er derfor en høy sannsynlighet for høye radonverdier i disse områdene. Her anbefaler Statens strålevern oppfølgende målinger i alle boliger med leilighet eller oppholdsrom i 1. etasje eller underetasje. Sør for Bones til Budal er under 5 % av målingene over tiltaksgrensen, og området har lav sannsynlighet for høye radonverdier. Anbefalt oppfølging kan her begrenses til generell informasjon og veiledning. I de resterende delene av kommunen er det en middels høy sannsynlighet for forhøyde radonnivåer, og det anbefales å gjøre oppfølgende målinger i utvalgte boliger. Line Ruden Gro Beate Ramberg Katrine Ånestad Terje Strand Kartlegging av radon i Midtre Gauldal kommune Mer generell informasjon om radon finnes 1. INNLEDNING på Strålevernets radonsider: http://radon.nrpa.no. 1.1 Om radon Radon (222Rn) er et radioaktivt stoff som dannes naturlig ved desintegrasjon av 1.2 Bakgrunn for prosjektet radium (226Ra), og som finnes i varierende I forbindelse med Nasjonal kreftplan, som mengder i all berggrunn og jordsmonn.