Research Collection
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Commission Implementing Regulation (EU)
L 229/6 EN Official Journal of the European Union 24.8.2012 REGULATIONS COMMISSION IMPLEMENTING REGULATION (EU) No 766/2012 of 24 July 2012 approving minor amendments to the specification for a name entered in the register of protected designations of origin and protected geographical indications [Patata di Bologna (PDO)] THE EUROPEAN COMMISSION, (3) The Commission has examined the amendment in question and decided that it is justified. Since this Having regard to the Treaty on the Functioning of the European concerns a minor amendment, in accordance with Union, Article 9(2) of Regulation (EC) No 510/2006, the Commission may adopt it without using the procedure Having regard to Council Regulation (EC) No 510/2006 of set out in Articles 6 and 7 of that Regulation, 20 March 2006 on the protection of geographical indications and designations of origin for agricultural products and food HAS ADOPTED THIS REGULATION: stuffs ( 1), and in particular the second sentence of Article 9(2) thereof, Article 1 Whereas: The specification for the protected designation of origin "Patata di Bologna" is hereby amended in accordance with Annex I to this Regulation. (1) In accordance with the first subparagraph of Article 9(1) of Regulation (EC) No 510/2006, the Commission has examined Italy’s application for the approval of Article 2 amendments to the specification for the protected desig The consolidated single document setting out the main points nation of origin "Patata di Bologna", registered under of the specification is set out in Annex II to this Regulation. Commission Regulation (EC) No 228/2010 ( 2). -

Mappa Opportunità Valli Del Savena Idice
A cura di: 7 Presentazione Stefano Agusto, Bruno Alampi, Caterina Benni, Paola Fornasari, Giulia Luisotti, Premessa Shaban Musaj, Barbara Pisani, Giulia Rezzadore, Eugenio Soldati, Giovanna Trombetti, Michele Zanoni coordinatore della ricerca (Area Sviluppo Economico - Città Prima parte metropolitana di Bologna) 9 Quadro conoscitivo del tessuto demografico e produttivo Grazietta Demaria dell’Unione dei Comuni Savena-Idice (Settore Strutture Tecnologiche Comunicazione e Servizi Strumentali - Città • Carta d’identità metropolitana di Bologna) • Il contesto demografico Fabio Boccafogli, Monica Mazzoni, Licia Nardi, Paola Varini • La struttura produttiva e il profilo delle aziende (Servizio Studi e Statistica per la Programmazione Strategica - Città metropolitana di • Movimento turistico e capacità ricettiva Bologna) • Punti salienti dell’analisi statistica Si ringraziano: UNIONE DEI COMUNI SAVENA-IDICE Viviana Boracci – Direttore Generale Indice Grazia Borghi – Area Risorse Economiche Giulia Naldi – Area Risorse Economiche Germana Pozzi – Responsabile sportello integrato Suap - Progetti d’Impresa Seconda parte ASL - DISTRETTO SAN LAZZARO DI SAVENA 34 Opportunità imprenditoriali: Paride Lorenzini – Responsabile Ufficio di Piano per la Salute ed il Benessere Sociale • Servizi alla persona ASSOCIAZIONI DI CATEGORIA FIRMATARIE DEL PATTO PER L’OCCUPAZIONE E LE • Manifattura, trasporti e servizi alle imprese OPPORTUNITÀ ECONOMICHE DELL’UNIONE DEI COMUNI SAVENA-IDICE • Agroalimentare e commercio alimentare Cia, Cna, Coldiretti, Confartigianato, -

Unione Dei Comuni Savena-Idice
Unione dei Comuni Savena-Idice SUAP ASSOCIATO Comuni di Loiano, Monghidoro, Monterenzio, Ozzano dell’Emilia, Pianoro Prot. 2016/0002550 Pianoro, 03/03/2016 Pratica SUAP n° 70/2015 Referente: Arch. Germana Pozzi INVIATA VIA PEC SPETT .LE ENERGIA VERDE S.R.L. VIA SAN CARLO N . 12/4 40023 CASTEL GUELFO DI BOLOGNA (BO) INVIATA VIA PEC SPETT .LE ING . MEZZINI ALBERTO VIA DELLA SCALETTA N . 16 40063 MONGHIDORO (BO) INVIATA VIA PEC E.P.C. SPETT .LE COMUNE DI MONGHIDORO VIA MATTEOTTI , 1 40063 MONGHIDORO (B O) C.A. SETTORE PROGRAMMAZIONE E GESTIONE DEL TERRITORIO SERVIZIO ASSETTO DEL TERRITORIO INVIATO VIA PEC E.P.C. SPETT .LE SOPRINTENDENZA PER I BENI ARCHITETTONICI E IL PAESAGGIO DELLE PROVINCIE DI BO-MO VIA IV NOVEMBRE 5 40123 BOLOGNA [email protected] INVIATO VIA PEC E.P.C. SPETT .LE COMUNE DI MONGHIDORO UFFICIO TECNICO Viale Risorgimento 1 – 40065 Pianoro (Bo) – Tel. 0516527711 – Fax 051774690 - C.F. 02961561202 email: [email protected] email certificate: [email protected] VIA MATTEOTTI , 1 40063 MONGHIDORO (BO) [email protected] INVIATO VIA PEC E.P.C. SPETT .LE ARPAE – SAC DI BOLOGNA VIA SAN FELICE 25 40122 BOLOGNA [email protected] INVIATO VIA PEC E.P.C. SPETT .LE REGIONE EMILIA ROMAGNA SERVIZIO TERRITORIALE AGRICOLTURA , CACCIA E PESCA DI BOLOGNA VIALE A. SILVANI 6 BOLOGNA [email protected] INVIATO VIA PEC E.P.C. SPETT .LE AUSL – DIPARTIMENTO DI SANITA ’ PUBBLICA VIA SEMINARIO 1 40068 SAN LAZZARO DI SAVENA (BO) [email protected] INVIATO VIA PEC E.P.C. -
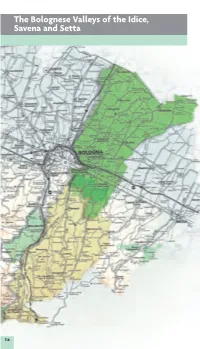
The Bolognese Valleys of the Idice, Savena and Setta
3_ eo_gb 0 008 3: 0 ag a The Bolognese Valleys of the Idice, Savena and Setta 114 _ dce_gb 0 008 3: 9 ag a 5 The Rivers the Futa state highway SS 65 and the road The valleys of the tributaries to the right of along the valley-bottom, which continues as the Reno punctuate the central area of the far as the Lake of Castel dell’Alpi, passing the Bolognese Apennines in a truly surprising majestic Gorges of Scascoli. Along the river, variety of colours and landscapes. They are there are numerous mills, some of which can the Idice, Savena and Setta Rivers, of which be visited, constructed over the centuries. only the Idice continues its course onto the Before entering the plains, the Savena cros- plains, as far as the Park of the Po Delta. ses the Regional Park of Bolognese Gypsums and Abbadessa Gullies, which is also crossed The Idice by the River Idice. The Idice starts on Monte Oggioli, near the Raticosa Pass, and is the largest of the rivers in these valleys. Interesting from a geologi- cal and naturalistic point of view, its valley offers many reasons for a visit. Particularly beautiful is the stretch of river where it joins the Zena Valley: this is where the Canale dei Mulini (mills) branches off, continuing alon- gside it until it reaches the plains, in the ter- ritory of San Lazzaro di Savena. Flowing through the Valleys of Campotto, the Idice finally joins the Reno. Here an interesting system of manmade basins stop the Reno’s water flowing into the Idice’s bed in dry periods. -

Testing a Calibration Approach for a Limited-Area
TESTING A CALIBRATION APPROACH FOR A LIMITED-AREA ENSEMBLE PRECIPITATION FORECAST USING REFORECASTS Tommaso Diomede, Chiara Marsigli, Andrea Montani, Tiziana Paccagnella ARPA-SIMC, HydroMeteorological and Climate Service of the Emilia-Romagna Regional Agency for Environmental Protection, Bologna, Italy E-mail: [email protected] Objective To implement a calibration technique for the precipitation output provided by COSMO-LEPS, the Limited-area Ensemble Prediction System based on the model COSMO. To investigate the potential of using reforecasts for the calibration of the ensemble precipitation forecast, especially with respect to the improvement of the forecast skill for rare events. To test three calibration techniques: Cumulative Distribution Function based corrections, Linear Regression and Analogs. Calibration strategy methodologies study areas data collection • choice of methodologies which enable a calibration of 24h quantitative precipitation • Emilia-Romagna Region (Northern Italy) • Observed precipitation forecasts (QPFs), not only of the probabilities of exceeding a threshold • Switzerland • Emilia-Romagna Region (1971-2007) aim: • Germany • Switzerland (1971-2007) • Germany (1989-2007) –improvement of COSMO-LEPS QPFs especially as an input for hydrological applications • COSMO-LEPS reforecast QPFs • 30 years (1971-2000) • selected methods: • 1 member, nested on ERA40, COSMO v4.0 • 1 run every three days (forecast range 90h) - Cumulative Distribution Function based corrections (CDF) [m] - Linear Regression (LR) • COSMO-LEPS -

Question for Written Answer
Question for written answer E-004061/2019 to the Commission Rule 138 Alessandra Basso (ID), Angelo Ciocca (ID), Alessandro Panza (ID), Elena Lizzi (ID), Antonio Maria Rinaldi (ID), Luisa Regimenti (ID), Marco Zanni (ID), Annalisa Tardino (ID), Rosanna Conte (ID), Mara Bizzotto (ID), Massimo Casanova (ID), Stefania Zambelli (ID), Isabella Tovaglieri (ID) Subject: Damage caused by bad weather in Emilia-Romagna In the second and third weeks of November, a series of exceptional rainstorms swept through the provinces of Bologna, Modena and Ferrara in Emilia-Romagna. The heavy rainfall caused rivers to rise, in particular the rivers Reno and Idice, and flooding of residential areas, for example in the municipality of Budrio, and of farmland around Finale Emilia; storm surges hit the area of Goro, in the province of Ferrara, causing beach erosion and the sinking of the dredge, which plays a crucial role in keeping clear the inlet in which important economic activities based on clam fishing are carried out. The cost of the damage appears to be high given the number of farms, maritime businesses and hotels affected in an area where agriculture and tourism are cornerstones of the local economy. In the light of the damage and the inconvenience caused to local people and businesses: 1. Will the Commission pledge full support from the EU Solidarity Fund for the regional authorities in Emilia-Romagna and local bodies involved in restoring economic activities and infrastructure? 2. Given the frequency with which adverse weather phenomena occur, what action will it take in the future, and what exceptional funding will it make available, to guarantee the safety of businesses and communities in Emilia-Romagna? PE645.377v01-00. -

Statuto Unione Dei Comuni Savena-Idice
UNIONE DEI COMUNI SAVENA-IDICE STATUTO Il Testo è stato approvato dai Consigli delle Amministrazioni Comunali costituenti l’Unione con i seguenti provvedimenti consiliari: Consiglio Comunale di Loiano Delibera n. 75 del 28/10/2014 Consiglio Comunale di Monghidoro Delibera n. 55 del 03/09/2014 Consiglio Comunale di Monterenzio Delibera n. 24 del 07/08/2014 Consiglio Comunale di Ozzano dell’Emilia Delibera n. 27 del 23/04/2014 Consiglio Comunale di Pianoro Delibera n. 13 del 26/03/2014 Consiglio Comunale di San Lazzaro di Savena Delibera n. 25 del 15/04/2014 Atti deliberativi pubblicati all’Albo Pretorio dei rispettivi Enti. INDICE TITOLO I° PRINCIPI FONDAMENTALI 4 ART. 1 ISTITUZIONE DELL’UNIONE DEI COMUNI DENOMINAZIONE – SEDE – STEMMA E GONFALONE 4 ART. 2 STATUTO E REGOLAMENTI 4 ART. 3 DURATA E SCIOGLIMENTO DELL’UNIONE 5 ART. 4 ADESIONE DI NUOVI COMUNI E RECESSO DALL’UNIONE 5 ART. 5 FINALITA’ E COMPITI DELL’UNIONE 6 ART. 6 FUNZIONI DELL’UNIONE 7 ART. 7 MODALITA’ DI ATTRIBUZIONE DELLE COMPETENZE ALL’UNIONE 8 TITOLO II° GLI ORGANI DI GOVERNO DELL’UNIONE 8 ART. 8 GLI ORGANI DI GOVERNO 8 ART. 9 COMPETENZE DEL CONSIGLIO 9 ART. 10 COMPOSIZIONE DEL CONSIGLIO 10 ART. 11 ELEZIONE, DIMISSIONI, SURROGAZIONE E 11 DURATA IN CARICA DEI CONSIGLIERI 11 ART. 12 DIRITTI E DOVERI DEL CONSIGLIERE 11 ART. 13 GARANZIA DELLE MINORANZE E CONTROLLO CONSILIARE 12 ART. 14 INCOMPATIBILITÀ A CONSIGLIERE DELL’UNIONE – CAUSE DI DECADENZA 12 ART. 15 CONVOCAZIONE E PRESIDENZA DELLE SEDUTE DEL CONSIGLIO IN ASSENZA DI GIUNTA IN CARICA 12 ART. 16 MODALITÀ DI CONVOCAZIONE DEL CONSIGLIO 13 ART. -

List of Rivers of Italy
Sl. No Name Draining Into Comments Half in Italy, half in Switzerland - After entering Switzerland, the Spöl drains into 1 Acqua Granda Black Sea the Inn, which meets the Danube in Germany. 2 Acquacheta Adriatic Sea 3 Acquafraggia Lake Como 4 Adda Tributaries of the Po (Left-hand tributaries) 5 Adda Lake Como 6 Adige Adriatic Sea 7 Agogna Tributaries of the Po (Left-hand tributaries) 8 Agri Ionian Sea 9 Ahr Tributaries of the Adige 10 Albano Lake Como 11 Alcantara Sicily 12 Alento Adriatic Sea 13 Alento Tyrrhenian Sea 14 Allaro Ionian Sea 15 Allia Tributaries of the Tiber 16 Alvo Ionian Sea 17 Amendolea Ionian Sea 18 Amusa Ionian Sea 19 Anapo Sicily 20 Aniene Tributaries of the Tiber 21 Antholzer Bach Tributaries of the Adige 22 Anza Lake Maggiore 23 Arda Tributaries of the Po (Right-hand tributaries) 24 Argentina The Ligurian Sea 25 Arno Tyrrhenian Sea 26 Arrone Tyrrhenian Sea 27 Arroscia The Ligurian Sea 28 Aso Adriatic Sea 29 Aterno-Pescara Adriatic Sea 30 Ausa Adriatic Sea 31 Ausa Adriatic Sea 32 Avisio Tributaries of the Adige 33 Bacchiglione Adriatic Sea 34 Baganza Tributaries of the Po (Right-hand tributaries) 35 Barbaira The Ligurian Sea 36 Basentello Ionian Sea 37 Basento Ionian Sea 38 Belbo Tributaries of the Po (Right-hand tributaries) 39 Belice Sicily 40 Bevera (Bévéra) The Ligurian Sea 41 Bidente-Ronco Adriatic Sea 42 Biferno Adriatic Sea 43 Bilioso Ionian Sea 44 Bisagno The Ligurian Sea 45 Biscubio Adriatic Sea 46 Bisenzio Tyrrhenian Sea 47 Boesio Lake Maggiore 48 Bogna Lake Maggiore 49 Bonamico Ionian Sea 50 Borbera Tributaries -

Unione Dei Comuni Savena–Idice
Comuni di: Loiano Unione dei Com u ni Monghidoro Monterenzio Savena–Idice Ozzano dell’Emilia Stazione Unica Appaltante Pianoro Prot. n. 3637/2017 PROCEDURA APERTA PER L’AFFIDAMENTO DEI LAVORI DI ADEGUAMENTO DEI PASSAGGI PEDONALI NELL’AMBITO DEL COMUNE DI OZZANO DELL’EMILIA DISCIPLINARE DI GARA CIG: 7016813942 La Stazione Unica Appaltante dell’Unione dei Comuni Savena – Idice (Stazione Appaltante), in ese- cuzione della determinazione a contrarre del Responsabile Settore Programmazione e Gestione del Territorio del Comune di Ozzano dell’Emilia (Ente Committente) n. 87 del 24.02.2017, indice una procedura aperta relativamente all’affidamento dei lavori di adeguamento dei passaggi pe- donali nell’ambito del territorio del Comune di Ozzano dell’Emilia. Art. 1 STAZIONE APPALTANTE Unione dei Comuni Savena-Idice – Stazione Appaltante Unica, Viale Risorgimento n. 1 – 40065 Pianoro (BO) – Tel. 0516527711 - www.uvsi.it - E-mail: stazioneappaltan- [email protected] – [email protected] - C.F. e P.I. 02961561202 - Codice NUTS ITD55. Art. 2 ENTE COMMITTENTE Comune di Ozzano dell'Emilia - Settore Programmazione e Gestione del Territorio – Ufficio Lavori pubblici – Servizi ambientali, Via della Repubblica, 10 - 40064 Ozzano dell'Emilia - tel. +39.051.791333 - www.comune.ozzano.bo.it PEC: [email protected]. Art. 3 INFORMAZIONI SULLA PROCEDURA E SUL CONTRATTO Tutta la documentazione è consultabile sul sito www.uvsi.it e sul sito www.comune.ozzano.bo.it Per ulteriori informazioni è possibile richiedere chiarimenti con le modalità di cui al successivo art. 23. Art. 4 SOPRALLUOGO Il sopralluogo è obbligatorio e potrà essere effettuato senza alcuna richiesta scritta. -

UNIONE DEI COMUNI SAVENA-IDICE (UMVSI BO) - Codice AOO: UMVSI BO AOO - Reg
UNIONE DEI COMUNI SAVENA-IDICE (UMVSI_BO) - Codice AOO: UMVSI_BO_AOO - Reg. nr.0004324/2018 del 16/03/2018 Comuni di: Loiano Monghidoro Unione dei Comuni Monterenzio Ozzano dell'Emilia Savena-Idice Pianoro Prot. n. 4324 Pianoro, lì 16/03/2018 Ai Sigg.ri Consiglieri dell'Unione dei Comuni Savena-Idice Loro Indirizzi Oggetto: Convocazione del Consiglio. Il Presidente Visto l'art. 16 comma 2 del vigente Statuto Convoca La seduta del Consiglio dell'Unione dei Comuni Savena-Idice presso la sede dell'ente in Viale Risorgimento, 1 - Pianoro per il giorno GIOVEDÌ 22/03/2018 alle ore 18:00 1) COMUNICAZIONE DEL PRESIDENTE AL CONSIGLIO; 2) APPROVAZIONE DEI VERBALI DELLA SEDUTA PRECEDENTE; 3) APPROVAZIONE DOCUMENTO UNICO DI PROGRAMMAZIONE 2018 - 2020 E DEL BILANCIO DI PREVISIONE FINANZIARIO 2018-2020 (ART. 151 DEL D.LGS. N. 267/2000 E ART. 10, D.LGS. N. 118/2011); 4) APPROVAZIONE SCHEMA DI CONVENZIONE TRA IL COMUNE DI SAN LAZZARO DI SAVENA, L'UNIONE DEI COMUNI SAVENA-IDICE E L'AZIENDA USL DI BOLOGNA – DISTRETTO DI COMMITTENZA E GARANZIA DI SAN LAZZARO DI SAVENA PER IL GOVERNO CONGIUNTO DELLE POLITICHE E DEGLI INTERVENTI SOCIO-SANITARI E PER LA GESTIONE DEL FONDO PER LA NON AUTOSUFFICIENZA. ANNO 2018; 5) APPROVAZIONE SCHEMA DI CONVENZIONE TRA L'UNIONE DEI COMUNI SAVENA-IDICE, IL COMUNE DI SAN LAZZARO DI SAVENA E L'AZIENDA USL DI BOLOGNA - DISTRETTO DI COMMITTENZA E GARANZIA SAN LAZZARO DI SAVENA, PER LA GESTIONE E LA REALIZZAZIONE DI PROGETTI RIENTRANTI NELLA PROGRAMMAZIONE SOCIO-SANITARIA DEL DISTRETTO SAN LAZZARO DI SAVENA, PER IL FUNZIONAMENTO DELL'UFFICIO DI PIANO (ORGANIZZAZIONE, DOTAZIONE ORGANICA, FUNZIONI, GESTIONE AMMINISTRATIVO-CONTABILE DEL BUDGET DISTRETTUALE) - ANNO 2018; Sede: Viale Risorgimento 1, 40065 Pianoro (BO) tel. -

Tunnels and Underground Cities
Tunnels and Underground Cities: Engineering and Innovation meet Archaeology, Architecture and Art – Peila, Viggiani & Celestino (Eds) © 2019 Taylor & Francis Group, London, ISBN 978-1-138-38865-9 Resilient city: The case of Bisagno diversion tunnel G. Lunardi, G. Cassani, M. Gatti, B. Spigarelli & C.L. Zenti Rocksoil S.p.A., Milan, Italy ABSTRACT: In today’s world of rapid environment changes, increasing urbanization and vulnerability, it is very crucial to embed the concept of resilience into the development plan- ning of our cities in order to have a sustainable development. Planning a city without a robust resilience strategy to cope from disasters is equivalent to wasting resources and putting people, infrastructure, assets and economy at risk. Resilience is the ability of a system, com- munity or society exposed to hazards to resist, absorb, accommodate, adapt to, transform and recover from the effects of a hazard in a timely and efficient manner. The Bisagno Valley has been historically affected by a number of flood events, which became particularly frequent in the last decade. This is mainly due to the urbanisation of the valley since the 1950s and the recent climate changes, with increased flash flood events. The paper describes the approach used on the Bisagno Diversion Tunnel Project Management, which involved stakeholder rela- tionships and integration at different levels, institutional frameworks and partnerships amongst all urban stakeholders, particularly planner architects, engineers, disaster and risk reduction management specialists, private sector, and communities to address risk reduction and resilience in a holistic manner. Risk reduction and resilience building save lives, enhance social and economic development, and provide equitable, prosperous and sustainable urban development. -

Genova: a New Logo
Genova: a new logo for new perspectives GENOA´S LOCAL ACTION PLAN IN THE FRAME OF URBACT-CITYLOGO Aarhus | Alba Iulia | Coimbra | Dundee | Genoa | Oslo | Utrecht | Vilnius | Warsaw | Zaragoza Report by City Logo Operative Team: Raffaella Cecconi, Sergio Di Paolo, Marisa Gardella, Chiara Martorana, Gianluca Saba, Cesare Torre. Municipality of Genova, Deputy Major for Tourism and Culture Department, Communication and City Promotion Division, Communication Office, International Affairs Office. Genova, March 2015 Table of content MAYOR’S SPEECH Creuza de Ma 1.1. EXECUTIVE SUMMARY 2. FRAMEWORK 2.1. Genoa: History, Changes and Perspectives 2.2. Belonging to the URBACT-CityLogo Project 2.3. The Genoa Local Support Group 3. PROBLEM ANALYSIS 3.1. New narrative for a city in transition 3.2. The need to attract visitors, investments, intelligence 3.3. The need for a new territorial marketing approach 4. LONG TERMS GOALS 4.1. Increase Genoa’s ability to attract 4.2. Develop coherent marketing strategy 4.3. Involving citizens in conveying their creative energies to welcoming strategies 5. SHORT/MEDIUM TERM OBJECTIVES 5.1. A new and effective visual identity for the city 5.1.1. A long history of circumstantial logos 5.2. Shared marketing plan 5.3. Providing ad-hoc governance, ensuring financing 6. ACTIVITIES IMPLEMETED AND COLLABORATIVE METHOD 6.1. LSG, focus groups, workshops and local media awareness 6.2. The City narrated by focus groups 6.3. Unveiling city’s truths in a collaborative way 6.4. From “focus groups” to workshops 6.5. Competition of ideas and urban visual identity 6.6. Organization of a memorable event for presentation of new city brand 6.7.