Re-Sampling of Inline Holographic Images for Improved Reconstruction Resolution
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
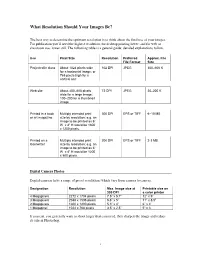
What Resolution Should Your Images Be?
What Resolution Should Your Images Be? The best way to determine the optimum resolution is to think about the final use of your images. For publication you’ll need the highest resolution, for desktop printing lower, and for web or classroom use, lower still. The following table is a general guide; detailed explanations follow. Use Pixel Size Resolution Preferred Approx. File File Format Size Projected in class About 1024 pixels wide 102 DPI JPEG 300–600 K for a horizontal image; or 768 pixels high for a vertical one Web site About 400–600 pixels 72 DPI JPEG 20–200 K wide for a large image; 100–200 for a thumbnail image Printed in a book Multiply intended print 300 DPI EPS or TIFF 6–10 MB or art magazine size by resolution; e.g. an image to be printed as 6” W x 4” H would be 1800 x 1200 pixels. Printed on a Multiply intended print 200 DPI EPS or TIFF 2-3 MB laserwriter size by resolution; e.g. an image to be printed as 6” W x 4” H would be 1200 x 800 pixels. Digital Camera Photos Digital cameras have a range of preset resolutions which vary from camera to camera. Designation Resolution Max. Image size at Printable size on 300 DPI a color printer 4 Megapixels 2272 x 1704 pixels 7.5” x 5.7” 12” x 9” 3 Megapixels 2048 x 1536 pixels 6.8” x 5” 11” x 8.5” 2 Megapixels 1600 x 1200 pixels 5.3” x 4” 6” x 4” 1 Megapixel 1024 x 768 pixels 3.5” x 2.5” 5” x 3 If you can, you generally want to shoot larger than you need, then sharpen the image and reduce its size in Photoshop. -

Invention of Digital Photograph
Invention of Digital photograph Digital photography uses cameras containing arrays of electronic photodetectors to capture images focused by a lens, as opposed to an exposure on photographic film. The captured images are digitized and stored as a computer file ready for further digital processing, viewing, electronic publishing, or digital printing. Until the advent of such technology, photographs were made by exposing light sensitive photographic film and paper, which was processed in liquid chemical solutions to develop and stabilize the image. Digital photographs are typically created solely by computer-based photoelectric and mechanical techniques, without wet bath chemical processing. The first consumer digital cameras were marketed in the late 1990s.[1] Professionals gravitated to digital slowly, and were won over when their professional work required using digital files to fulfill the demands of employers and/or clients, for faster turn- around than conventional methods would allow.[2] Starting around 2000, digital cameras were incorporated in cell phones and in the following years, cell phone cameras became widespread, particularly due to their connectivity to social media websites and email. Since 2010, the digital point-and-shoot and DSLR formats have also seen competition from the mirrorless digital camera format, which typically provides better image quality than the point-and-shoot or cell phone formats but comes in a smaller size and shape than the typical DSLR. Many mirrorless cameras accept interchangeable lenses and have advanced features through an electronic viewfinder, which replaces the through-the-lens finder image of the SLR format. While digital photography has only relatively recently become mainstream, the late 20th century saw many small developments leading to its creation. -

1/2-Inch Megapixel CMOS Digital Image Sensor
MT9M001: 1/2-Inch Megapixel Digital Image Sensor Features 1/2-Inch Megapixel CMOS Digital Image Sensor MT9M001C12STM (Monochrome) Datasheet, Rev. M For the latest datasheet, please visit www.onsemi.com Features Table 1: Key Performance Parameters Parameter Value • Array Format (5:4): 1,280H x 1,024V (1,310,720 active Optical format 1/2-inch (5:4) pixels). Total (incl. dark pixels): 1,312H x 1,048V Active imager size 6.66 mm (H) x 5.32 mm (V) (1,374,976 pixels) • Frame Rate: 30 fps progressive scan; programmable Active pixels 1,280 H x 1,024 V • Shutter: Electronic Rolling Shutter (ERS) Pixel size 5.2 m x 5.2 m • Window Size: SXGA; programmable to any smaller Shutter type Electronic rolling shutter (ERS) Maximum data rate/ format (VGA, QVGA, CIF, QCIF, etc.) 48 MPS/48 MHz • Programmable Controls: Gain, frame rate, frame size master clock Frame SXGA 30 fps progressive scan; rate (1280 x 1024) programmable Applications ADC resolution 10-bit, on-chip Responsivity 2.1 V/lux-sec • Digital still cameras Dynamic range 68.2 dB • Digital video cameras •PC cameras SNRMAX 45 dB Supply voltage 3.0 V3.6 V, 3.3 V nominal 363 mW at 3.3 V (operating); Power consumption General Description 294 W (standby) Operating temperature 0°C to +70°C The ON Semiconductor MT9M001 is an SXGA-format with a 1/2-inch CMOS active-pixel digital image sen- Packaging 48-pin CLCC sor. The active imaging pixel array of 1,280H x 1,024V. It The sensor can be operated in its default mode or pro- incorporates sophisticated camera functions on-chip grammed by the user for frame size, exposure, gain set- such as windowing, column and row skip mode, and ting, and other parameters. -

More About Digital Cameras Image Characteristics Several Important
More about Digital Cameras Image Characteristics Several important characteristics of digital images include: Physical Size How big is the image that has been captured, as measured in inches or pixels? File Size How large is the computer file that makes up the image, as measured in kilobytes or megabytes? Pixels All digital images taken with a digital camera are made up of pixels (short for picture elements). A pixel is the smallest part (sometimes called a point or a dot) of a digital image and the total number of pixels make up the image and help determine its size and its resolution, or how much information is included in the image when we view it. Generally speaking, the larger the number of pixels an image contains, the sharper it will appear, especially when it is enlarged, which is what happens when we want to print our photographs larger than will fit into small 3 1\2 X 5 inch or 5 X 7 inch frames. You will notice in the first picture below that the Grand Canyon is in sharp focus and there is a large amount of detail in the image. However, when the image is enlarged to an extreme level, the individual pixels that make up the image are visible--and the image is no longer clear and sharp. Megapixels The term megapixels means one million pixels. When we discuss how sharp a digital image is or how much resolution it has, we usually refer to the number of megapixels that make up the image. One of the biggest selling features of digital cameras is the number of megapixels it is capable of producing when a picture is taken. -

Oxnard Course Outline
Course ID: DMS R120B Curriculum Committee Approval Date: 04/25/2018 Catalog Start Date: Fall 2018 COURSE OUTLINE OXNARD COLLEGE I. Course Identification and Justification: A. Proposed course id: DMS R120B Banner title: AdobePhotoShop II Full title: Adobe PhotoShop II B. Reason(s) course is offered: This course provides the development of skills necessary to combine the use of Photoshop digital image editing software with Adobe LightRoom's expanded digital photographic image editing abilities. These skills will enhance a student’s ability to enter into employment positions such as web master, graphics design, and digital image processing. C. C-ID: 1. C-ID Descriptor: 2. C-ID Status: D. Co-listed as: Current: None II. Catalog Information: A. Units: Current: 3.00 B. Course Hours: 1. In-Class Contact Hours: Lecture: 43.75 Activity: 0 Lab: 26.25 2. Total In-Class Contact Hours: 70 3. Total Outside-of-Class Hours: 87.5 4. Total Student Learning Hours: 157.5 C. Prerequisites, Corequisites, Advisories, and Limitations on Enrollment: 1. Prerequisites Current: DMS R120A: Adobe Photoshop I 2. Corequisites Current: 3. Advisories: Current: 4. Limitations on Enrollment: Current: D. Catalog description: Current: This course will continue the development of students’ skills in the use of Adobe Photoshop digital image editing software by integrating the enhanced editing capabilities of Adobe Lightroom into the Adobe Photoshop workflow. Students will learn how to “punch up” colors in specific areas of digital photographs, how to make dull-looking shots vibrant, remove distracting objects, straighten skewed shots and how to use Photoshop and Lightroom to create panoramas, edit Adobe raw DNG photos on mobile device, and apply Boundary Wrap to a merged panorama to prevent loss of detail in the image among other skills. -

Use and Analysis of Color Models in Image Processing
cess Pro ing d & o o T F e c f h o Sharma and Nayyer, J Food Process Technol 2015, 7:1 n l o a l n o DOI: 10.4172/2157-7110.1000533 r Journal of Food g u y o J Processing & Technology ISSN: 2157-7110 Perspective Open Access Use and Analysis of Color Models in Image Processing Bhubneshwar Sharma* and Rupali Nayyer Department of Electronics and Communication Engineering, S.S.C.E.T, Punjab Technical University, India Abstract The use of color image processing is divided by two factors. First color is used in object identification and simplifies extraction from a scene and color is powerful descriptor. Second, humans can use thousands of color shades and intensities. Color Image Processing is divided into two areas full color and pseudo-color processing. In this processing various color models are used that are based on color recognition, color components etc. A few papers on various applications such as lane detection, face detection, fruit quality evaluation etc based on these color models have been published. A survey on widely used models RGB, HSI, HSV, RGI, etc. is represented in this paper. Keywords: Image processing; Color models; RGB; HIS; HSV; RGI for matter surfaces, while ignoring ambient light, normalized RGB is invariant (under certain assumptions) to changes of surface orientation Introduction relatively to the light source. This, together with the transformation An image may be defined as a two dimensional function, f(x, y), simplicity helped this color space to gain popularity among the where x and y are spatial coordinates and the amplitude of f at any researchers [5-7] (Figure 1). -

ELEC 7450 - Digital Image Processing Image Acquisition
I indirect imaging techniques, e.g., MRI (Fourier), CT (Backprojection) I physical quantities other than intensities are measured I computation leads to 2-D map displayed as intensity Image acquisition Digital images are acquired by I direct digital acquisition (digital still/video cameras), or I scanning material acquired as analog signals (slides, photographs, etc.). I In both cases, the digital sensing element is one of the following: Line array Area array Single sensor Stanley J. Reeves ELEC 7450 - Digital Image Processing Image acquisition Digital images are acquired by I direct digital acquisition (digital still/video cameras), or I scanning material acquired as analog signals (slides, photographs, etc.). I In both cases, the digital sensing element is one of the following: Line array Area array Single sensor I indirect imaging techniques, e.g., MRI (Fourier), CT (Backprojection) I physical quantities other than intensities are measured I computation leads to 2-D map displayed as intensity Stanley J. Reeves ELEC 7450 - Digital Image Processing Single sensor acquisition Stanley J. Reeves ELEC 7450 - Digital Image Processing Linear array acquisition Stanley J. Reeves ELEC 7450 - Digital Image Processing Two types of quantization: I spatial: limited number of pixels I gray-level: limited number of bits to represent intensity at a pixel Array sensor acquisition I Irradiance incident at each photo-site is integrated over time I Resulting array of intensities is moved out of sensor array and into a buffer I Quantized intensities are stored as a grayscale image Stanley J. Reeves ELEC 7450 - Digital Image Processing Array sensor acquisition I Irradiance incident at each photo-site is integrated over time I Resulting array of intensities is moved out of sensor array and into a buffer I Quantized Two types of quantization: intensities are stored as a I spatial: limited number of pixels grayscale image I gray-level: limited number of bits to represent intensity at a pixel Stanley J. -

CMOS Image Sensor a Complementary Metal Oxide Semiconductor (CMOS) Image Sensor Is an Electronic Device That Converts Light Intensity Into a Digital Signal
CMOS Image Sensor A complementary metal oxide semiconductor (CMOS) image sensor is an electronic device that converts light intensity into a digital signal. A CMOS image sensor is made up of pixels and supporting circuitry. Each pixel has three photodiodes and an operational amplifier. The supporting circuitry consists of an reset/sample pin, matrix selection switches, an output gain amplifier, and an analog to digital converter (ADC). The entire CMOS image sensor is contained in a standard integrated circuit package and is, placed on printed circuit boards (PCBs). The circuit components on the CMOS image sensor are all contained within this package, and external pins are used to access and control the image sensor. CMOS Image sensors are typically used with a shutter lens, and external computing system to display and process the output image of the image sensor. 1) Pixels A pixel consists of three photodiodes, and an operational amplifier. Each photodiode is covered in a filter that only allows in one color of light. The three photodiodes in a pixel either have a red, green, or blue filter. The CMOS image sensors in modern smartphones contain millions of these individual pixels arranged in a matrix format. ● Photodiode A photodiode is a light sensitive device that creates an electrical charge from light energy. The electric charge produces a small current that relates to the intensity of light observed by the photodiode. This current is unusable without initial signal conditioning from a transimpedance amplifier. ● Transimpedance Amplifier A transimpedance amplifier is a standard operational amplifier put into a transimpedance configuration. A transimpedance amplifier is able to accept a small current, and transform it into an analog voltage. -

Digital Image Guidance for EPA Civil Inspections and Investigations
Office of Compliance Digital Image Guidance for EPA Civil Inspections and Field Investigations Number: OECA-GUID-2017-001-R1 06/13/2017 U.S. Environmental Protection Agency OECA Page 1 of 33 Digital Image Guidance Effective Date: June 13, 2017 OECA-GUID-2017-001-R1 Page Intentionally Blank OECA Page 2 of 33 Digital Image Guidance Effective Date: June 13, 2017 OECA-GUID-2017-001-R1 Revision History This table shows changes to this controlled document over time. The most recent version is presented in the top row of the table. Previous versions of the document are maintained by the OECA Document Control Coordinator. History Effective Date Digital Image Guidance for EPA Civil Inspections and Field 06/13/2017 Investigations, Revision 1 Revisions to reflect changes in technology (e.g. memory devices and formatting) and EPA policies (e.g. information security and records management). 2006 Digital Image Guidance for EPA Civil Inspections and Field Investigations, Original Issue OECA Page 3 of 33 Digital Image Guidance Effective Date: June 13, 2017 OECA-GUID-2017-001-R1 CONTENTS DISCLAIMER..................................................................................................................................... 5 PURPOSE OF GUIDANCE ................................................................................................................. 5 INTRODUCTION ............................................................................................................................... 6 Technical Information .................................................................................................................... -

Digital Image Basics
Chapter 1 Digital Image Basics 1.1 What is a Digital Image? To understand what a digital image is, we have to first realize that what we see when we look at a \digital image" is actually a physical image reconstructed from a digital image. The digital image itself is really a data structure within the computer, containing a number or code for each pixel or picture element in the image. This code determines the color of that pixel. Each pixel can be thought of as a discrete sample of a continuous real image. It is helpful to think about the common ways that a digital image is created. Some of the main ways are via a digital camera, a page or slide scanner, a 3D rendering program, or a paint or drawing package. The simplest process to understand is the one used by the digital camera. Figure 1.1 diagrams how a digital image is made with a digital camera. The camera is aimed at a scene in the world, and light from the scene is focused onto the camera's picture plane by the lens (Figure 1.1a). The camera's picture plane contains photosensors arranged in a grid-like array, with one sensor for each pixel in the resulting image (Figure 1.1b). Each sensor emits a voltage proportional to the intensity of the light falling on it, and an analog to digital conversion circuit converts the voltage to a binary code or number suitable for storage in a cell of computer memory. This code is called the pixel's value. -

Interfacing a CMOS Sensor to the TMS320DM642 Using Raw Capture Mode Miguel Hernandez IV Device Applications
Application Report SPRAA52A − January 2010 Interfacing a CMOS Sensor to the TMS320DM642 Using Raw Capture Mode Miguel Hernandez IV Device Applications ABSTRACT This document contains information on how to interface the TMS320DM642 to a CMOS Digital Image Sensor in raw capture mode. A complete example is shown, including hardware and software interfaces. The software consists of a set of routines that are compatible with the Video Port Mini-Driver and External Device Control interface. The discussed interface is proven and has been tested from 320x240 at 120 frames per second to 1920x1080 at 19 frames per second. This document is accompanied by example software designed to operate with the TMS320DM642 EVM and is available electronically from the TI website. Project collateral discussed in this application report can be downloaded from the following URL: http://www.ti.com/lit/zip/SPRAA52. Contents 1 Introduction . 2 2 CMOS Digital Image Sensor Overview ........................................................................................ 3 2.1 CMOS Sensor Signal Descriptions ......................................................................................... 3 2.2 CMOS Sensor Register Descriptions ...................................................................................... 4 2.2.1 Row and Column Size ................................................................................................. 5 2.2.2 Horizontal and Vertical Blanking .................................................................................. 5 -

Digital Image Processing Question & Answers GRIET/ECE 1 1. Explain
for more :- http://www.UandiStar.org Digital Image Processing Question & Answers 1. Explain about color fundamentals. Color of an object is determined by the nature of the light reflected from it. When a beam of sunlight passes through a glass prism, the emerging beam of light is not white but consists instead of a continuous spectrum of colors ranging from violet at one end to red at the other. As Fig. 5.1.1 shows, the color spectrum may be divided into six broad regions: violet, blue, green, yellow, orange, and red. When viewed in full color (Fig. 5.1.2), no color in the spectrum ends abruptly, but rather each color blends smoothly into the next. Fig. 5.1.1 Color spectrum seen by passing white light through a prism. Fig. 5.1.2 Wavelengths comprising the visible range of the electromagnetic spectrum. As illustrated in Fig. 5.1.2, visible light is composed of a relatively narrow band of frequencies in the electromagnetic spectrum. A body that reflects light that is balanced in all visible wavelengths appears white to the observer. However, a body that favors reflectance in a limited range of the visible spectrum exhibits some shades of color. For example, green objects reflect light with wavelengths primarily in the 500 to 570 nm range while absorbing most of the energy at other wavelengths. Characterization of light is central to the science of color. If the light is achromatic (void of color), its only attribute is its intensity, or amount. Achromatic light is what viewers see on a black and white television set.