DOCSLIB.ORG

The Planck Mass and the Chandrasekhar Limit

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Planck Mass and the Chandrasekhar Limit The Planck mass and the Chandrasekhar limit ͒ David Garfinklea Department of Physics, Oakland University, Rochester, Michigan 48309 ͑Received 6 November 2008; accepted 10 March 2009͒ The Planck mass is often assumed to play a role only at the extremely high energy scales where quantum gravity becomes important. However, this mass plays a role in any physical system that involves gravity, quantum mechanics, and relativity. We examine the role of the Planck mass in determining the maximum mass of white dwarf stars. © 2009 American Association of Physics Teachers. ͓DOI: 10.1119/1.3110884͔ I. INTRODUCTION ery part of the gas is in equilibrium and thus must have zero net force on it. In particular, consider a small disk of the gas The Planck mass, length, and time can be constructed with base area A and thickness dr at a distance r from the from the Newton gravitational constant G, the Planck con- center of the ball. Denote the mass of the disk by m , and the ប 1 d stant , and the speed of light c. In particular, the Planck mass of all the gas at radii smaller than r by M͑r͒. Newton mass, MP is given by showed that the disk would be gravitationally attracted by បc the gas at radii smaller than r, but unaffected by the gas at M = ͱ . ͑1͒ radii larger than r, and the force on the disk would be the P G same as if all the mass at radii smaller than r were concen- The Planck mass is very small on the human scale because trated at the center. In other words, the inward force due to Ϸ −8 MP 10 kg. It is quite large on the scale of elementary gravity on the disk has a magnitude / Ϸ 19 particles because MP mH 10 , where mH is the mass of a GM͑r͒m d ͑ ͒ hydrogen atom. This large ratio is often referred to as the Fin = 2 . 2 “hierarchy problem;” the “problem” is that such a large ratio r seems unnatural and thus requires an explanation. Because ␳ The volume of the disk is Adr, and so we have md = Adr, present day particle accelerators probe energies correspond- where ␳ is the density of the gas at radius r. Thus using Eq. 2 ing to a few hundred mHc , present day accelerators are very ͑2͒ we find 2 far from the much higher scale of MPc , the energy scale at GM͑r͒␳Adr which quantum gravity becomes important. F = . ͑3͒ One might expect that the Planck mass occurs only in very in r2 exotic, highly speculative, and completely theoretical areas of physics. However, because the Planck mass is constructed If gravity is pulling the disk inward, then why does it not fall G ប c and the whole gas ball collapse? Because pressure differ- from only , , and , it occurs in cases where gravity, ͑ ͒ quantum mechanics, and relativity all play an essential role. ences push the disk outward. Let P r be the pressure of the One such problem is the Chandrasekhar limit, the maximum gas as a function of radius. Then the outward force exerted mass of a white dwarf star.2 All stars are held in equilibrium on the inner surface of the disk is P͑r͒A. This force is almost by the opposing forces of self-gravity and pressure. Thus but not exactly balanced by the inward force of P͑r+dr͒A. gravity plays a role in the properties of stars. In white dwarf The net outward force on the disk due to pressure is stars the pressure is supplied by the motion of electrons due dP ͑ ͒ ͑ ͒ ͑ ͒ to the uncertainty principle and the Pauli exclusion principle. Fout = P r A − P r + dr A =−A dr. 4 Thus quantum mechanics plays a role. In the most extreme dr white dwarf stars, those nearing the maximum possible mass, Because the inward force and outward force must cancel and the electrons are moving so fast that their speeds are compa- thus must have equal magnitudes, it follows that Fin=Fout, rable to the speed of light, and thus relativity plays an essen- and therefore tial role. In this paper we will give a simple derivation of the Chan- dP GM͑r͒␳ =− . ͑5͒ drasekhar limit and show its connection with the Planck dr r2 mass. We define N ϵM /m and call this large dimension- h P H ͑ ͒ less number the hierarchy number. Nature also presents us As we increase r to r+dr, M r increases because the mass with another large dimensionless number: the maximum contained within that radius is augmented by a thin shell of number of nucleons ͑protons and neutrons͒ in a white dwarf radius r and thickness dr. Such a shell has volume 4␲r2dr, star, which we will call the Chandrasekhar number and de- and because the density at that radius is ␳, it follows that Ϸ 3 M͑r+dr͒−M͑r͒=4␲␳r2dr,or note as NC. We can show that NC 0.774Nh. We will show how this result comes about and specifically the roles of G, dM͑r͒ ប, and c in the calculation. =4␲r2␳. ͑6͒ dr II. GRAVITATION Suppose that the matter that makes up the star is so simple that the pressure is a function only of the density ͑and not the We start with some 19th century physics—the equilibrium temperature͒. If we know the equation of state P͑␳͒,wecan configurations for spherical balls of self-gravitating gas.3 Ev- rewrite Eq. ͑5͒ as 683 Am. J. Phys. 77 ͑8͒, August 2009 http://aapt.org/ajp © 2009 American Association of Physics Teachers 683 dP d␳ GM͑r͒␳ N ␳ ͑ ͒ ͑ ͒ =− 2 . 7 = . 12 d␳ dr r V 2mH We then multiply Eq. ͑7͒ by r2 /͑G␳͒, differentiate with re- Hence, we can write Eq. ͑11͒ as ͑ ͒ 2Uץ spect to r, and use Eq. 6 to obtain dP V = . ͑13͒ V2ץ d r2 dP d␳ d␳ ␳ 1 ͩ ͪ + ␳ =0. ͑8͒ 4␲Gr2 dr ␳ d␳ dr ͑ ͒ ϰ −1/3 From Eq. 9 it follows that pmax V and therefore that ץ Equation ͑8͒ allows us to make a mathematical model of the pmax 1 pmax ␳ =− . ͑14͒ V 3 Vץ star. Choose a value of the central density c and integrate Eq. ͑8͒ outward until the pressure vanishes at the surface of the star. Complete the model by assuming vacuum at all radii We apply Eq. ͑13͒ to Eq. ͑10͒ and use Eq. ͑14͒ and straight- ␳ larger than this stellar surface. Each value of c yields one forward algebra and obtain stellar model. dP 1 d⑀ = p4ͯ ͯ . ͑15͒ d␳ 9␲2ប3␳ dp p=pmax III. QUANTUM MECHANICS IV. SPECIAL RELATIVITY Matter in a white dwarf consists of electrons and nuclei, ͑ ͒ ͑ ͒ / ␳ mostly of carbon and oxygen. Because the matter is electri- Equation 15 with pmax given by Eq. 9 gives dP d ,if cally neutral, there is one proton for every electron. Also we have an expression for ⑀͑p͒. In nonrelativistic mechanics ⑀ 2 /͑ ͒ because the number of neutrons equals the number of pro- =p 2me , where me denotes the mass of the electron. In tons for both carbon and oxygen nuclei, there is one neutron relativistic mechanics for each electron. Usually the pressure of a gas depends on ⑀ ͱ 2 2 2 4 ͑ ͒ its temperature. However, the pressure at low temperatures is = p c + mec , 16 a purely quantum mechanical effect that is independent of and thus temperature. Recall that the uncertainty principle implies that 2 particles confined to a box must have a momentum. Because d⑀ c p = . ͑17͒ faster moving particles have larger energy, it takes work to dp ͱp2c2 + m2c4 make the box smaller. This work is due to the pressure. e Consider N electrons along with N protons and N neutrons We can gain insight by expressing Eq. ͑15͒ in terms of combined in carbon and oxygen nuclei confined to a cubical dimensionless quantities that have factored out the relevant box of side L. The electrons are free particles except for the physical scales. We define the dimensionless quantity X as confining walls of the box. Because of the Pauli exclusion p principle, each state can have no more than two electrons. X = max . ͑18͒ Thus for N electrons the ground state energy U is obtained mec / by putting the N electrons in the N 2 states of lowest energy. It follows from Eq. ͑9͒ that As shown in standard textbooks on statistical mechanics, the ␳ maximum momentum of an electron in the ground state pmax X3 = , ͑19͒ ͑which is the Fermi momentum͒ is given by ˜␳ ប ␳ ͑ ␲2 ͒1/3 ͑ ͒ where the constant ˜ is given by pmax = 3 N , 9 L 2 m ˜␳ = H , ͑20͒ ␲2 ␭3 and the ground state energy is given by 3 e 3 p ␭ 1 L max and e is the Compton wavelength of the electron given by U = ͩ ͪ ͵ ⑀͑p͒p2dp, ͑10͒ ␲2 ប ប 0 ␭ = . ͑21͒ e m c where ⑀͑p͒ is the energy of a single particle. e What we want to calculate is not U itself, but dP/d␳. It is straightforward to see the physical meaning of the scale -V, it follows that ˜␳: By the uncertainty principle, we expect electrons to acץ/Uץ−=Because P quire relativistic speeds at number densities on the order of 2Uץ dP =− . ͑11͒ one electron per cubic Compton wavelength. Because there -V are two nucleons per electron, this number density of elecץ␳ץ d␳ trons occurs at a mass density ˜␳ that is of the order of m per ͑ 3 ͒ H Here V=L is the volume of the box.
Load more

Recommended publications
  • Musings on the Planck Length Universe
    Musings on the Planck Length Universe -How does matter, or how does a change move through space on the micro- level? The answer depends on how the structure of space and matter are defined at a certain order of magnitude and what are their properties at that level. We will assume that, on the micro-level, the limits of space are discrete, consisting of the smallest units possible. Therefore, in order to define the structure of space on this level it would be necessary to introduce a notion of an “elementary spatial unit” (ESU), the smallest part of space, some kind of spatial “atom”. This would be the smallest and indivisible finite part (cell) of space, defined only by size and position (neighborhoods). It doesn’t have any content, but it could be filled with some property like “matter” or “vacuum”. There are two possibilities in which a property can to move through space (change its position). One would be that an ESU itself, containing a certain property, moves between other ESU carrying its content like a fish moving through the water or a ball through the air. Another possibility would be that the positions of all the ESU don’t change while their content is moving. This would be like an old billboard covered with light bulbs, or a screen with pixels. The positions of the bulbs or pixels are fixed, and only their content (light) changes position from one bulb to the other. Here the spatial structure (the structure of positions) is fixed and it is only the property (the content) that changes positions, thus moving through space.
    [Show full text]
  • Six Easy Roads to the Planck Scale
    Six easy roads to the Planck scale Ronald J. Adler∗ Hansen Laboratory for Experimental Physics Gravity Probe B Mission, Stanford University, Stanford California 94309 Abstract We give six arguments that the Planck scale should be viewed as a fundamental minimum or boundary for the classical concept of spacetime, beyond which quantum effects cannot be neglected and the basic nature of spacetime must be reconsidered. The arguments are elementary, heuristic, and plausible, and as much as possible rely on only general principles of quantum theory and gravity theory. The paper is primarily pedagogical, and its main goal is to give physics students, non-specialists, engineers etc. an awareness and appreciation of the Planck scale and the role it should play in present and future theories of quantum spacetime and quantum gravity. arXiv:1001.1205v1 [gr-qc] 8 Jan 2010 1 I. INTRODUCTION Max Planck first noted in 18991,2 the existence of a system of units based on the three fundamental constants, G = 6:67 × 10−11Nm2=kg2(or m3=kg s2) (1) c = 3:00 × 108m=s h = 6:60 × 10−34Js(or kg m2=s) These constants are dimensionally independent in the sense that no combination is dimen- sionless and a length, a time, and a mass, may be constructed from them. Specifically, using ~ ≡ h=2π = 1:05 × 10−34Js in preference to h, the Planck scale is r r G G l = ~ = 1:6 × 10−35m; T = ~ = 0:54 × 10−43; (2) P c3 P c5 r c M = ~ = 2:2 × 10−8kg P G 2 19 3 The energy associated with the Planck mass is EP = MP c = 1:2 × 10 GeV .
    [Show full text]
  • Chapter 3 Why Physics Is the Easiest Science  Effective Theories
    CHAPTER 3 WHY PHYSICS IS THE EASIEST SCIENCE EFFECTIVE THEORIES If we had to understand the whole physical universe at once in order to understand any part of it, we would have made little progress. Suppose that the properties of atoms depended on their history, or whether they were in stars or people or labs we might not understand them yet. In many areas of biology and ecology and other fields systems are influenced by many factors, and of course the behavior of people is dominated by our interactions with others. In these areas progress comes more slowly. The physical world, on the other hand, can be studied in segments that hardly affect one another, as we will emphasize in this chapter. If our goal is learning how things work, a segmented approach is very fruitful. That is one of several reasons why physics began earlier in history than other sciences, and has made considerable progress it really is the easiest science. (Other reasons in addition to the focus of this chapter include the relative ease with which experiments can change one quantity at a time, holding others fixed; the relative ease with which experiments can be repeated and improved when the implications are unclear; and the high likelihood that results are described by simple mathematics, allowing testable predictions to be deduced.) Once we understand each segment we can connect several of them and unify our understanding, a unification based on real understanding of how the parts of the world behave rather than on philosophical speculation. The history of physics could be written as a process of tackling the separate areas once the technology and available understanding allow them to be studied, followed by the continual unification of segments into a larger whole.
    [Show full text]
  • CHIME and Probing the Origin of Fast Radio Bursts by Liam Dean Connor a Thesis Submitted in Conformity with the Requirements
    CHIME and Probing the Origin of Fast Radio Bursts by Liam Dean Connor A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Astronomy and Astrophysics University of Toronto c Copyright 2016 by Liam Dean Connor Abstract CHIME and Probing the Origin of Fast Radio Bursts Liam Dean Connor Doctor of Philosophy Graduate Department of Astronomy and Astrophysics University of Toronto 2016 The time-variable long-wavelength sky harbours a number of known but unsolved astro- physical problems, and surely many more undiscovered phenomena. With modern tools such problems will become tractable, and new classes of astronomical objects will be revealed. These tools include digital telescopes made from powerful computing clusters, and improved theoretical methods. In this thesis we employ such devices to understand better several puzzles in the time-domain radio sky. Our primary focus is on the origin of fast radio bursts (FRBs), a new class of transients of which there seem to be thousands per sky per day. We offer a model in which FRBs are extragalactic but non-cosmological pulsars in young supernova remnants. Since this theoretical work was done, observations have corroborated the picture of FRBs as young rotating neutron stars, including the non-Poissonian repetition of FRB 121102. We also present statistical arguments regard- ing the nature and location of FRBs. These include reinstituting the classic V=Vmax-test @ log N to measure the brightness distribution of FRBs, i.e., constraining @ log S . We find consis- tency with a Euclidean distribution. This means current observations cannot distinguish between a cosmological population and a more local uniform population, unless added assumptions are made.
    [Show full text]
  • Neutron Stars & Black Holes
    Introduction ? Recall that White Dwarfs are the second most common type of star. ? They are the remains of medium-sized stars - hydrogen fused to helium Neutron Stars - failed to ignite carbon - drove away their envelopes to from planetary nebulae & - collapsed and cooled to form White Dwarfs ? The more massive a White Dwarf, the smaller its radius Black Holes ? Stars more massive than the Chandrasekhar limit of 1.4 solar masses cannot be White Dwarfs Formation of Neutron Stars As the core of a massive star (residual mass greater than 1.4 ?Supernova 1987A solar masses) begins to collapse: (arrow) in the Large - density quickly reaches that of a white dwarf Magellanic Cloud was - but weight is too great to be supported by degenerate the first supernova electrons visible to the naked eye - collapse of core continues; atomic nuclei are broken apart since 1604. by gamma rays - Almost instantaneously, the increasing density forces freed electrons to absorb electrons to form neutrons - the star blasts away in a supernova explosion leaving behind a neutron star. Properties of Neutron Stars Crab Nebula ? Neutrons stars predicted to have a radius of about 10 km ? In CE 1054, Chinese and a density of 1014 g/cm3 . astronomers saw a ? This density is about the same as the nucleus supernova ? A sugar-cube-sized lump of this material would weigh 100 ? Pulsar is at center (arrow) million tons ? It is very energetic; pulses ? The mass of a neutron star cannot be more than 2-3 solar are detectable at visual masses wavelengths ? Neutron stars are predicted to rotate very fast, to be very ? Inset image taken by hot, and have a strong magnetic field.
    [Show full text]
  • Gy Use Units and the Scales of Ener
    The Basics: SI Units A tour of the energy landscape Units and Energy, power, force, pressure CO2 and other greenhouse gases conversion The many forms of energy Common sense and computation 8.21 Lecture 2 Units and the Scales of Energy Use September 11, 2009 8.21 Lecture 2: Units and the scales of energy use 1 The Basics: SI Units A tour of the energy landscape Units and Energy, power, force, pressure CO2 and other greenhouse gases conversion The many forms of energy Common sense and computation Outline • The basics: SI units • The principal players:gy ener , power, force, pressure • The many forms of energy • A tour of the energy landscape: From the macroworld to our world • CO2 and other greenhouse gases: measurements, units, energy connection • Perspectives on energy issues --- common sense and conversion factors 8.21 Lecture 2: Units and the scales of energy use 2 The Basics: SI Units tour of the energy landscapeA Units and , force, pressure, powerEnergy CO2 and other greenhouse gases conversion The many forms of energy Common sense and computation SI ≡ International System MKSA = MeterKilogram, , Second,mpereA Unit s Not cgs“English” or units! Electromagnetic units Deriud v n e its ⇒ Char⇒ geCoulombs EnerJ gy oul es ⇒ Current ⇒ Amperes Po werW a tts ⇒ Electrostatic potentialV⇒ olts Pr e ssuP a r s e cals ⇒ Resistance ⇒ Ohms Fo rNe c e wto n s T h erma l un i ts More about these next... TemperatureK⇒ elvinK) ( 8.21 Lecture 2: Units and the scales of energy use 3 The Basics: SI Units A tour of the energy landscape Units and Energy, power,
    [Show full text]
  • Study of Pulsar Wind Nebulae in Very-High-Energy Gamma-Rays with H.E.S.S
    Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S. Michelle Tsirou To cite this version: Michelle Tsirou. Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S.. As- trophysics [astro-ph]. Université Montpellier, 2019. English. NNT : 2019MONTS096. tel-02493959 HAL Id: tel-02493959 https://tel.archives-ouvertes.fr/tel-02493959 Submitted on 28 Feb 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE POUR OBTENIR LE GRADE DE DOCTEUR DE L’UNIVERSITÉ DE MONTPELLIER En Astrophysiques École doctorale I2S Unité de recherche UMR 5299 Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S. Présentée par Michelle TSIROU Le 17 octobre 2019 Sous la direction de Yves A. GALLANT Devant le jury composé de Elena AMATO, Chercheur, INAF - Acetri Rapporteur Arache DJANNATI-ATAȈ, Directeur de recherche, APC - Paris Examinateur Yves GALLANT, Directeur de recherche, LUPM - Montpellier Directeur de thèse Marianne LEMOINE-GOUMARD, Chargée de recherche, CENBG - Bordeaux Rapporteur Alexandre MARCOWITH, Directeur de recherche, LUPM - Montpellier Président du jury Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S.1 Michelle Tsirou 1High Energy Stereoscopic System To my former and subsequent selves, may this wrenched duality amalgamate ultimately.
    [Show full text]
  • Orders of Magnitude (Length) - Wikipedia
    03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre
    [Show full text]
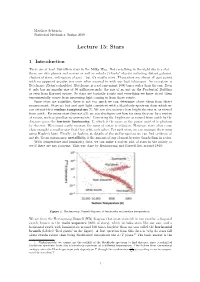
  • Lecture 15: Stars
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 15: Stars 1 Introduction There are at least 100 billion stars in the Milky Way. Not everything in the night sky is a star there are also planets and moons as well as nebula (cloudy objects including distant galaxies, clusters of stars, and regions of gas) but it's mostly stars. These stars are almost all just points with no apparent angular size even when zoomed in with our best telescopes. An exception is Betelgeuse (Orion's shoulder). Betelgeuse is a red supergiant 1000 times wider than the sun. Even it only has an angular size of 50 milliarcseconds: the size of an ant on the Prudential Building as seen from Harvard square. So stars are basically points and everything we know about them experimentally comes from measuring light coming in from those points. Since stars are pointlike, there is not too much we can determine about them from direct measurement. Stars are hot and emit light consistent with a blackbody spectrum from which we can extract their surface temperature Ts. We can also measure how bright the star is, as viewed from earth . For many stars (but not all), we can also gure out how far away they are by a variety of means, such as parallax measurements.1 Correcting the brightness as viewed from earth by the distance gives the intrinsic luminosity, L, which is the same as the power emitted in photons by the star. We cannot easily measure the mass of a star in isolation. However, stars often come close enough to another star that they orbit each other.
    [Show full text]
  • Compact Stars and the Evolution of Binary Systems
    Bull. Astr. Soc. India (2011) 39, 1–20 Compact stars and the evolution of binary systems E. P. J. van den Heuvel Astronomical Institute, “Anton Pannekoek”, University of Amsterdam, The Netherlands Received 2011 January 31; accepted 2011 February 27 Abstract. The Chandrasekhar limit is of key importance for the evolution of white dwarfs in binary systems and for the formation of neutron stars and black holes in bi- naries. Mass transfer can drive a white dwarf in a binary over the Chandrasekhar limit, which may lead to a Type Ia supernova (in case of a CO white dwarf) or an Accretion- Induced Collapse (AIC, in the case of an O-Ne-Mg white dwarf; and possibly also in some CO white dwarfs) which produces a neutron star. The direct formation of neu- tron stars or black holes out of degenerate stellar cores that exceed the Chandrasekhar limit, occurs in binaries with components that started out with masses ¸ 8 M¯. This paper first discusses possible models for Type Ia supernovae, and then focusses on the formation of neutron stars in binary systems, by direct core collapse and by the AIC of O-Ne-Mg white dwarfs in binaries. Observational evidence is re- viewed for the existence of two different direct neutron-star formation mechanisms in binaries: (i) by electron-capture collapse of the degenerate O-Ne-Mg core in stars with initial masses in the range of 8 to about 12 M¯, and (ii) by iron-core collapse in stars with inital masses above this range. Observations of neutron stars in binaries are consistent with a picture in which neutron stars produced by e-capture collapse have relatively low masses, »1.25 M¯, and received hardly any velocity kick at birth, whereas neutron stars produced by iron-core collapses are more massive and received large velocity kicks at birth.
    [Show full text]
  • Newton's Law of Gravitation Gravitation – Introduction
    Physics 106 Lecture 9 Newton’s Law of Gravitation SJ 7th Ed.: Chap 13.1 to 2, 13.4 to 5 • Historical overview • N’Newton’s inverse-square law of graviiitation Force Gravitational acceleration “g” • Superposition • Gravitation near the Earth’s surface • Gravitation inside the Earth (concentric shells) • Gravitational potential energy Related to the force by integration A conservative force means it is path independent Escape velocity Gravitation – Introduction Why do things fall? Why doesn’t everything fall to the center of the Earth? What holds the Earth (and the rest of the Universe) together? Why are there stars, planets and galaxies, not just dilute gas? Aristotle – Earthly physics is different from celestial physics Kepler – 3 laws of planetary motion, Sun at the center. Numerical fit/no theory Newton – English, 1665 (age 23) • Physical Laws are the same everywhere in the universe (same laws for legendary falling apple and planets in solar orbit, etc). • Invented differential and integral calculus (so did Liebnitz) • Proposed the law of “universal gravitation” • Deduced Kepler’s laws of planetary motion • Revolutionized “Enlightenment” thought for 250 years Reason ÅÆ prediction and control, versus faith and speculation Revolutionary view of clockwork, deterministic universe (now dated) Einstein - Newton + 250 years (1915, age 35) General Relativity – mass is a form of concentrated energy (E=mc2), gravitation is a distortion of space-time that bends light and permits black holes (gravitational collapse). Planck, Bohr, Heisenberg, et al – Quantum mechanics (1900–27) Energy & angular momentum come in fixed bundles (quanta): atomic orbits, spin, photons, etc. Particle-wave duality: determinism breaks down.
    [Show full text]
  • Lesson 2: Temperature
    Lesson 2: Temperature Notes from Prof. Susskind video lectures publicly available on YouTube 1 Units of temperature and entropy Let’s spend a few minutes talking about units, in partic- ular the Boltzmann constant kB, a question about which last chapter ended with. What is the Boltzmann constant? Like many constants in physics, kB is a conversion factor. The speed of light is a conversion factor from distances to times. If something is going at the speed of light, and in a time t covers a distance x, then we have x = ct (1) And of course if we judiciously choose our units, we can set c = 1. Typically these constants are conversion factors from what we can call human units to units in some sense more fun- damental. Human units are convenient for scales and mag- nitudes of quantities which people can access reasonably easily. We haven’t talked about temperature yet, which is the sub- ject of this lesson. But let’s also say something about the units of temperature, and see where kB – which will simply be denoted k when there is no possible confusion – enters the picture. Units of temperature were invented by Fahren- heit1 and by Celsius2, in both cases based on physical phe- 1Daniel Gabriel Fahrenheit (1686 - 1736), Polish-born Dutch physicist and engineer. 2Anders Celsius (1701 - 1744), Swedish physicist and astronomer. 2 nomena that people could easily monitor. The units we use in physics laboratories nowadays are Kelvin3 units, which are Celsius or centrigrade degrees just shifted by an additive constant, so that the 0 °C of freezing water is 273:15 K and 0 K is absolute zero.
    [Show full text]