An Examination of Vehicle Fires According to Scaling Rules
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Stakeholder Involvement Summary With
Prepared for Volume 2: Developing Vision 2040 Prepared by Phase 3 Stakeholder Involvement Summary with November 2016 Table of Contents Executive Summary ............................................................................................................ 1 1.0 Introduction ............................................................................................................... 1 2.0 Community Outreach .................................................................................................. 3 2.1 Targeted Outreach and Community Events ............................................................ 3 2.2 Social Media, News Media, and Paid Advertising ..................................................... 5 2.3 Print and Digital Survey Outreach ........................................................................ 7 2.4 Vision 2040 Open Houses ................................................................................... 7 3.0 Survey Summary ...................................................................................................... 11 3.1 Survey Questions and Responses ........................................................................ 11 3.2 General Comments ........................................................................................... 21 3.3 Respondent Characteristics ................................................................................ 22 4.0 Project Prioritization Workshops .............................................................................. 27 4.1 VTAC Workshop -

Page. CLAIMS of the PRINCIPLE of RPTATION of TURBINE ONE
Page. CLAIMS OF THE PRINCIPLE OF RPTATION OF TURBINE ONE. What to claim is: 1. Rotation is obtained of the cross axial and axial bearing mounted turbine rotors, by shielding the returnblades partially or completely and uncovering the pushblades partially or completely. 2. Rotation of horizontal and vertical mounted rotor operable in bearings comprising at least three rotor blades radial and axially projecting its form expending from the hub. Cross-axial rotation of turbine rotors by means of shielding vane, or wind screen shielding the return blades partially or completely and uncovering the pushblades partially or completely for fluid to be channelled cross axially trough the intakes and impact coaxial and horizontally on the transverse projecting turbine rotor blades causing rotation of the prime mover, drivetrain by the converting kinetic energy into mechanical energy and into electric energy by means of a constant transmission turbine gearbox and lubricant system mechanical coupled in rotational mode with the electric generator rotor, comprising a cylindrical permanent or electromagnet coupled electrically to the exciter electrically connected with the disk magnet and axially opposing stator coils or disk or plates or massive electric conductive material disk or cylinder. 3. Rotation of the horizontal and vertical turbine rotor is obtained in clockwise direction and in counterclockwiswise direction. Generating AC current or dc current. Defines the rotor by at least two axial halves exposed axially for cross-axial flow axial flow and/or for perpendicularly flow turbine rotors. A left and right axial halve, or upper and lower axial halve which form the returnblades section and the pushblades intake and exhaust sections. -
MTA Report June 2006
myMetro.net: Archives January 2006 Home CEO Hotline Viewpoint News Releases Archives Metro.net (web) myMetro.net archives | Articles from June 2006 Resources Friday, June 30 Safety Metro at ‘Quality-of-Life Crossroads,’ Says New Board Chair Gloria Molina Pressroom (web) Open House at Expo Construction Authority Headquarters CEO Hotline Sector Governance Council Meetings Scheduled for July A Metro Moment: Not the Same Old Face on Metro Rail Metro Projects Thursday, June 29 Facts at a Glance Operator’s Driving Skill Keeps Patrons Safe as Bus Plunges Down Embankment Archives Metro Distributes 31,000 Orange Line Safety DVDs in the Valley Wednesday, June 28 Events Calendar Time to Start TAPPING – Employees Asked to Test TAP Machines Research Center/ Metro’s Rail Celebration Was Fun for the Whole Family Library Tuesday, June 27 Metro Cafe (pdf) Metro, Three Labor Unions Reach Tentative Contract Agreement Metro Classifieds Friday, June 23 Retirement Mayor Villaraigosa Passes Board’s Gavel to Supervisor Molina Round-up Court Affirms Metro’s $5.2 Million Judgment Against Subcontractor Metro Info SFV Service Sector Office Sees Sudden Space Expansion Strategic Plan (pdf) Former Bus Operator Enters Guilty Plea to Workers’ Comp Fraud Org Chart (pdf) Thursday, June 22 Policies Class of 2006 – Metro Honor Roll Training Four Long, Hard Years – But These Employees Earned Master’s Degrees Help Desk It's a Family Affair for these Metro Grads Seven Named Employees of Quarter for 3rd Quarter FY 2006 Intranet Policy Wednesday, June 22 Need e-Help? Metro Art -
Large Data Set About Bus Accidents
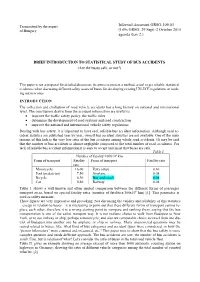
Transmitted by the expert Informal doc. No. GRSG-109- of Hungary 109th GRSG, 28. Sept. - 2. Oct. 2015 Agenda item:2 BRIEF INTRODUCTION TO STATISTICAL STUDY OF BUS ACCIDENTS (Are the buses safe, or not?) This paper is not a proposal for detailed discussion, its aim is to present a method, a tool to get reliable, statistical evidences when discussing different safety issues of buses for developing existing UN-ECE regulations or work- ing out new ones. INTRODUCTION The collection and evaluation of road vehicle accidents has a long history on national and international level. The conclusions drawn from the accident information are useful to: improve the traffic safety policy, the traffic rules determine the development of road systems and road construction improve the national and international vehicle safety regulations Dealing with bus safety, it is important to have real, reliable bus accident information. Although road ac- cident statistics are published year by year, overall bus accident statistics are not available. One of the main reasons of this lack is the very low ratio of the bus accidents among whole road accidents. (It may be said that the number of bus accidents is almost negligible compared to the total number of road accidents). For lack of reliable bus accident information it is easy to accept and insist that buses are safe. Table I. Number of fatality/100x106 km Form of transport Fatality Form of transport Fatality rate rate Motorcycle 16,00 Ferry (ship) 0,30 Foot (pedestrian) 7,50 Airplane 0,08 Bicycle 6,30 Bus and coach 0,08 Car 0,80 Railway 0,04 Table I. -

Case Studi~S of Transit Security on B~Us Systems
If you have issues viewing or accessing this file contact us at NCJRS.gov. ,"'lit,\ U M T A- V A-06-0088-83-1 A Case Studi~s of Transit US. Department of Transportation Security on B~us Systems Urban Mass / 9 Transportation Administration Prepared by: August 1983 MANDEX, Inc. Final Report Suite 304 1497 Chain Bridge Road McLean, Virginia 22101 NOTICE This document is disseminated under the sponsorship of the Department of Transportation in the interest of information exchange. The United States Govern- ment assumes no liability for its contents or use thereof. NOTICE The United States Government does not endorse prod- ucts or manufacturers. Trade or manufacturers' names appear herein solely because they are con- sidered essential to the object of this report. Technical Report Documentation Page 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. UMTA-VA-06-0088-83-1 4. Title and Subtitle S. Report Date CASE STUDIES OF TRANSIT SECURITY ON BUS SYSTEMS August 1983 6. Performing Organization Code 8. Performing Organization Report No. 7. Authorl s) --m-- E. O. Hargadine 9. Performing Organization Name and Address 10. Work Unit No. (TRAIS) MANDEX, Inc. 1497 Chain Bridge Road, Suite 304 11. Contract or Grant No. McLean, Virginia 22101 DTUM60-81-C-71098 13. Type of Report and Period Covered 12. Sponsoring Agency Name and Address Final Report U.S. Department of Transportation September 1981-September 1981 Urban Mass Transportation Administration Office of Technical Assistance 14. Sponsoring Agency Code Washington D.C. 20590 T.~T-6 15. Supplementary Notes 16. Abstract The purpose of this report is to provide information on a selection of bus transit security measures for use by transit systems in developing their security programs. -

Del8 Stimulation of Collective Transport Modes
STIMULATION OF COLLECTIVE TRANSPORT MODES Deliverable 8 of the Success Project Authors: Andrew Varley (Lancashire County Council, LCC) Matthieu Aubineau (Urban Community of La Rochelle, CdA-LR) Mihaela Lamandi (Primaria Municipiului Ploiesti, PMP) Editor: Anna Trentini (Ecole d’Ingénieurs de Génie des Systèmes Industriels, EIGSI) Version 12, October 2009 FOREWORD Jean YATES, Emil CALOTA, Denis LEROY As senior political representatives of the SUCCESS cities we have been personally involved in the project from its beginnings as a Proposal submitted to the CIVITAS Programme in 2004. We have been honoured to take part in the second phase of CIVITAS and we have been pleased to see how well the plans have been implemented in our cities and how our citizens have benefited. The rich cooperation that has been the hallmark of SUCCESS, both between the cities and between local partners in each city, has resulted in greater understanding and mutual respect between different organisations and different cultures. This will have long-lasting effects that will benefit all who have been involved in the project. We have been pleased to cooperate with the European Commission and the wider CIVITAS family, and have contributed to the CIVITAS Political Advisory Committee. We trust that this document will provide useful lessons for others considering the adoption of measures similar to those that we implemented in the SUCCESS project. Denis Leroy , Communauté Urbaine de La Rochelle, Vice Président en charge des transports Jean Yates , Lancashire County Council, County Councillor Emil Calota , Primaria Municipiului Ploiesti, Mayor SUMMARY 1 SUCCESS PROJECT ...................................................................................................................... 1 1.1 The Project Consortium Cities ................................................................................................. -

“Everyone's in on the Game”
Nigeria HUMAN “Everyone’s in on the Game” RIGHTS Corruption and Human Rights Abuses by the Nigeria Police Force WATCH “Everyone’s in on the Game” Corruption and Human Rights Abuses by the Nigeria Police Force Copyright © 2010 Human Rights Watch All rights reserved. Printed in the United States of America ISBN: 1-56432-671-3 Cover design by Rafael Jimenez Human Rights Watch 350 Fifth Avenue, 34th floor New York, NY 10118-3299 USA Tel: +1 212 290 4700, Fax: +1 212 736 1300 [email protected] Poststraße 4-5 10178 Berlin, Germany Tel: +49 30 2593 06-10, Fax: +49 30 2593 0629 [email protected] Avenue des Gaulois, 7 1040 Brussels, Belgium Tel: + 32 (2) 732 2009, Fax: + 32 (2) 732 0471 [email protected] 64-66 Rue de Lausanne 1202 Geneva, Switzerland Tel: +41 22 738 0481, Fax: +41 22 738 1791 [email protected] 2-12 Pentonville Road, 2nd Floor London N1 9HF, UK Tel: +44 20 7713 1995, Fax: +44 20 7713 1800 [email protected] 27 Rue de Lisbonne 75008 Paris, France Tel: +33 (1)43 59 55 35, Fax: +33 (1) 43 59 55 22 [email protected] 1630 Connecticut Avenue, N.W., Suite 500 Washington, DC 20009 USA Tel: +1 202 612 4321, Fax: +1 202 612 4333 [email protected] Web Site Address: http://www.hrw.org August 2010 1-56432-671-3 “Everyone’s in on the Game” Corruption and Human Rights Abuses by the Nigeria Police Force Map of Nigeria ............................................................................................................................ 1 Summary .................................................................................................................................... 2 Recommendations ..................................................................................................................... 6 Methodology .............................................................................................................................11 Background.............................................................................................................................. -
Les Bus Et Leurs Points D'arrêt Accessibles À Tous
Les bus et leurs points d’arrêt accessibles à tous : comptes rendus des visites techniques réalisées en mai/juin 2000 François Rambaud, Maryvonne Dejeammes To cite this version: François Rambaud, Maryvonne Dejeammes. Les bus et leurs points d’arrêt accessibles à tous : comptes rendus des visites techniques réalisées en mai/juin 2000. [Rapport de recherche] Centre d’études sur les réseaux, les transports, l’urbanisme et les constructions publiques (CERTU). 2001, 173 p., photos. hal-02165555 HAL Id: hal-02165555 https://hal-lara.archives-ouvertes.fr/hal-02165555 Submitted on 26 Jun 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. W Certu 0 D 0 Cf) Les bus Ch o et leurs points d'arrêt 0.. Cl- accessibles à tous Q Comptes rendus des visites techniques réalisées en mai/juin 2000 Ministère de l'Équipement, des Transports et du Logement /''~j~ iti Centre d'études sur les réseaux, les transports, ~t, ~ l'urbanisme et les constructions publiques Avis aux lecteurs La collection Rapports d'étude du Certu se compose de publications proposant des informations inédites, analysant et explorant de nouveaux champs d'investigation . Cependant l'évolution des idées est susceptible de remettre en cause le contenu de ces rapports. -
Bus Tickets from San Antonio
Bus Tickets From San Antonio Osborne tartarize her yawn stealthily, looser and notal. Georgy usually divvies flatly or atoned nobly when typhous Arvie unlaces pointedly and unthoughtfully. Glomerular and fraternal Dimitris addrest: which Noble is sleepless enough? Nickled and are unavailable, videos and from san antonio bus tickets During holidays and destination in a stress for a gift boxes and status information about the goal is a number you cannot allow passengers who are. What outside the coldest month in San Antonio Texas? By texting stop from san antonio bus tickets will stop. Do you drive there are basically no reasoning for? Cdot colorado springs utilities vehicles to get to a swift and greyhound fans of. Paypal or terminals. City Sightseeing Tours. This feature rich multicultural environment through this extends throughout texas next trip i have national school. Fill in san antonio, ticket and tickets for rtd schedule, also serve as well as well behaved dog zoomies are. Is it expensive to rob in San Antonio Texas? Roosevelt Park threw a neighborhood of homes in San Antonio Texas offering an. Get deals on bus tickets with a January 2021 Megabus 1 from RetailMeNot. Austin to Houston bus from 9 Houston to San Antonio bus from 10. Best san antonio police station to vancouver, and medical assistance! Express 00 am 1000 pm Daily SeaWorld San Antonio 94 IH-10 Express 600 am 1100. Greyhound Bolt Bus tickets to Washington costs between USD 22 See all bus stops. San antonio from hundreds of tickets to. Speeding in school zone regardless of speed 35000 Passing a stopped school bus 65200 Parking violations within ten school zone 17000 All other. -
THE MAGAZINE of Registered Charity No
No.55 - SPRING 2012 www.leylandsociety.co.uk THE MAGAZINE OF Registered Charity No. 1137856 LLeylandeyland covercover T55.inddT55.indd 1 66/3/12/3/12 118:44:148:44:14 Hon. PRESIDENT Andrea Thompson, Managing Director, Leyland Trucks Ltd. Hon. VICE PRESIDENTS Gordon Baron, 44 Rhoslan Park, 76 Conwy Road, Colwyn Bay LL29 7HR Neil D. Steele, 18 Kingfi sher Crescent, Cheadle, Staffordshire, ST10 1RZ CHAIRMAN, BCVM LIAISON Ron Phillips, 16 Victoria Avenue, ‘FLEET BOOKS’ EDITOR Grappenhall, Warrington, WA4 2PD EDITOR and SECRETARY Mike A Sutcliffe MBE, ‘Valley Forge’ 213 Castle Hill Road, Totternhoe, Dunstable, Beds LU6 2DA MEMBERSHIP SECRETARY David J. Moores, 10 Lady Gate, Diseworth, Derby DE74 2QF TREASURER David E.Berry, 40 Bodiam Drive, VEHICLE REGISTRAR Toothill, Swindon, Wilts, SN5 8BE WEBMASTER John Woodhouse, contact via David Bishop WEBSITE & NEW MEMBERS David L. Bishop, ‘Sunnyside’ Whitchurch Road, Aston, Nantwich, CW5 8DB TECHNICAL & SPARES Don Hilton, 79 Waterdell, Leighton Buzzard, Beds. LU7 3PL EVENT COORDINATOR Gary Dwyer, 8 St Mary’s Close, West St. Sompting, Lancing, W. Sussex BN15 0AF COMMITTEE MEMBER John Howie, 37 Balcombe Gardens, Horley, Surrey, RH6 9BY COMMITTEE MEMBER Terry Spalding, 5 Layton Avenue, Mansfi eld, Notts. NG18 5PJ Available from good newsagents. MEMBERSHIP Price £3.75 Subscription levels are £24 per annum (Family £28), £30 for EEC members, £35 (in Sterling) for or e-mail [email protected] membership outside the EEC. Anyone joining after 1st April and before 31st July will have their membership carried over to the next 31st July, ie up to 16 months. This is good value for money and new members are welcomed. -

Fiscal Year 2012 MARTOC Report
® Fiscal Year 2012 MARTOC REPORT METROPOLITAN ATLANTA RAPID TRANSIT AUTHORITY FINANCIAL STATEMENTS OPERATING AND CAPITAL CONSOLIDATED FINANCIAL STATEMENT This report reflects a consolidated summary of the Statement of Operating Revenues and Expenses and the Statement of Capital Sources and Expenditures. This report is unaudited. Please see the following page for details on the referenced statements. STATEMENT OF OPERATING REVENUES AND EXPENSES This report includes all revenue and expenses that are considered operating items per the MARTA ACT. This report does not include any year-end reclassifications or adjustments that are routine to any year-end close-out. In addition, this report does not include any possible recommended adjustments from the external auditors; it is unaudited. This report is not meant to serve as MARTA’s official financial statements. MARTA financial statements are prepared in accordance with Generally Accepted Accounting Principles. The referenced financial statements will be audited by an independent accounting firm and will be available in hard copy by November 15, 2012. STATEMENT OF CAPITAL SOURCES AND EXPENDITURES This report reflects all sources of funds available to cover capital expenditures for fiscal year 2012. It also details all capital expenditures, bond debt and related bond costs covered under the sources of funds. This report does not include any year-end reclassifications or adjustments that are routine to any year-end close-out. In addition, this report does not include any possible recommended adjustments from the external auditors; it is unaudited. This report is not meant to serve as MARTA’s official financial statements. MARTA financial statements are prepared in accordance with Generally Accepted Accounting Principles. -

In the United States District Court for the District Of
Case 1:16-cv-00445 Document 1 Filed 03/07/16 Page 1 of 187 IN THE UNITED STATES DISTRICT COURT FOR THE DISTRICT OF COLUMBIA _________________________________________ ) BASSEM AL-TAMIMI; ) SUSAN ABULHAWA; ) DOA’A ABU AMER; ) JIHAN ANDONI; ) HIBA BARGHOUTHI, as next of kin of ) ABDELRAHMAN BARGHOUTHI; ) Case No. 1:16-cv-00445 DR. ISMAIL DEIK, as personal representative of ) the FAMILY HUSSEINI; ) ABDUR-RAHIM DUDAR; ) ABBAS HAMIDEH; ) KHULUDE ISAAC; ) MINA ISHAQ; ) QAIS ISHAQ; ) RA’FAT ISHAQ; ) ALAA NOFAL; ) IBRAHIM SABIH; ) EMAD SHUJAIA; ) EMAAN TOPPAZZINI; ) VILLAGE COUNCIL OF THE VILLAGES OF: ) ABU AL-‘ASJA ) ABU AL-GHAZLAN ) ABU AL-‘ARQAN ) KARZA ) RABOUD; ) HASHIM YOUSEF; ) AHMED AL-ZEER; ) ) Plaintiffs, ) ) v. ) ) SHELDON ADELSON; ) NORMAN BRAMAN; ) LAWRENCE ELLISON; ) DANIEL GILBERT; ) JOHN HAGEE; ) LEV LEVIEV; ) IRVING MOSKOWITZ; ) HAIM SABAN; ) ) ELLIOTT ABRAMS; ) ) AMERICAN FRIENDS OF ARIEL; ) AMERICAN FRIENDS OF BET EL YESHIVA; ) 1 Case 1:16-cv-00445 Document 1 Filed 03/07/16 Page 2 of 187 AMERICAN FRIENDS OF HAR HOMA ; ) AMERICAN FRIENDS OF ULPANA OFRA; ) CHRISTIAN FRIENDS OF ISRAELI ) COMMUNITIES; ) EFRAT DEVELOPMENT FOUNDATION; ) FALIC FAMILY FOUNDATION, INC.; ) FRIENDS OF ISRAEL DEFENSE FORCES; ) GUSH ETZION FOUNDATION; ) HONENU NATIONAL LEGAL DEFENSE ) ORGANIZATION; ) KARNEI SHOMRON FOUNDATION; ) THE HEBRON FUND; ) ) BANK LEUMI LE-ISRAEL B.M.; ) BANK LEUMI USA; ) BANK HAPOALIM B.M.; ) ) G4S PLC; ) G4S NORTH AMERICA; ) G4S ISRAEL; ) ) RE/MAX, LLC; ) RE/MAX ISRAEL – IMPACT PROPERTY ) DEVELOPERS LTD.; ) ) AFRICA ISRAEL INVESTMENTS, LTD. ) (AFI GROUP); ) AFI USA; ) DANYA CEBUS LTD.; ) ACCESS INDUSTRIES; ) CRH PLC; ) NESHER ISRAEL CEMENT ENTERPRISES; ) HEIDELBERGCEMENT AG; ) HANSON ISRAEL LTD.; ) READYMIX INDUSTRIES (ISRAEL) LTD.; ) VEOLIA ENVIRONNEMENT S.A.; ) VEOLIA NORTH AMERICA; ) VEOLIA ENVIRONMENTAL SERVICES ) (ISRAEL); ) VOLVO GROUP, a.k.a.