To Download the PDF File
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Roger Page Cricket Books
ROGER PAGE DEALER IN NEW AND SECOND-HAND CRICKET BOOKS 10 EKARI COURT, YALLAMBIE, VICTORIA, 3085 TELEPHONE: (03) 9435 6332 FAX: (03) 9432 2050 EMAIL: [email protected] ABN 95 007 799 336 OCTOBER 2016 CATALOGUE Unless otherwise stated, all books in good condition & bound in cloth boards. Books once sold cannot be returned or exchanged. G.S.T. of 10% to be added to all listed prices for purchases within Australia. Postage is charged on all orders. For parcels l - 2kgs. in weight, the following rates apply: within Victoria $14:00; to New South Wales & South Australia $16.00; to the Brisbane metropolitan area and to Tasmania $18.00; to other parts of Queensland $22; to Western Australia & the Northern Territory $24.00; to New Zealand $40; and to other overseas countries $50.00. Overseas remittances - bank drafts in Australian currency - should be made payable at the Commonwealth Bank, Greensborough, Victoria, 3088. Mastercard and Visa accepted. This List is a selection of current stock. Enquiries for other items are welcome. Cricket books and collections purchased. A. ANNUALS AND PERIODICALS $ ¢ 1. A.C.S International Cricket Year Books: a. 1986 (lst edition) to 1995 inc. 20.00 ea b. 2014, 2015, 2016 70.00 ea 2. Athletic News Cricket Annuals: a. 1900, 1903 (fair condition), 1913, 1914, 1919 50.00 ea b. 1922 to 1929 inc. 30.00 ea c. 1930 to 1939 inc. 25.00 ea 3. Australian Cricket Digest (ed) Lawrie Colliver: a. 2012-13, 2013-14, 2014-15, 25.00 ea. b. 2015-2016 30.00 ea 4. -

Extract Catalogue for Auction
Page:1 May 19, 2019 Lot Type Grading Description Est $A CRICKET - AUSTRALIA - 1949 Onwards Ex Lot 94 94 1955-66 Melbourne Cricket Club membership badges complete run 1955-56 to 1965-66, all the scarce Country memberships. Very fine condition. (11) 120 95 1960 'The Tied Test', Australia v West Indies, 1st Test at Brisbane, display comprising action picture signed by Wes Hall & Richie Benaud, limited edition 372/1000, window mounted, framed & glazed, overall 88x63cm. With CoA. 100 Lot 96 96 1972-73 Jack Ryder Medal dinner menu for the inaugural medal presentation with 18 signatures including Jack Ryder, Don Bradman, Bill Ponsford, Lindsay Hassett and inaugural winner Ron Bird. Very scarce. 200 Lot 97 97 1977 Centenary Test collection including Autograph Book with 254 signatures of current & former Test players including Harold Larwood, Percy Fender, Peter May, Clarrie Grimmett, Ray Lindwall, Richie Benaud, Bill Brown; entree cards (4), dinner menu, programme & book. 250 98 - Print 'Melbourne Cricket Club 1877' with c37 signatures including Harold Larwood, Denis Compton, Len Hutton, Ted Dexter & Ross Edwards; window mounted, framed & glazed, overall 75x58cm. 100 99 - Strip of 5 reserved seat tickets, one for each day of the Centenary Test, Australia v England at MCG on 12th-17th March, framed, overall 27x55cm. Plus another framed display with 9 reserved seat tickets. (2) 150 100 - 'Great Moments' poster, with signatures of captains Greg Chappell & Tony Greig, limited edition 49/550, framed & glazed, overall 112x86cm. 150 Page:2 www.abacusauctions.com.au May 19, 2019 CRICKET - AUSTRALIA - 1949 Onwards (continued) Lot Type Grading Description Est $A Ex Lot 101 101 1977-86 Photographs noted Australian team photos (6) from 1977-1986; framed photos of Ray Bright (6) including press photo of Bright's 100th match for Victoria (becoming Victoria's most capped player, overtaking Bill Lawry's 99); artworks of cricketer & two-up player. -

Issue 40: Summer 2009/10
Journal of the Melbourne Cricket Club Library Issue 40, Summer 2009 This Issue From our Summer 2009/10 edition Ken Williams looks at the fi rst Pakistan tour of Australia, 45 years ago. We also pay tribute to Richie Benaud's role in cricket, as he undertakes his last Test series of ball-by-ball commentary and wish him luck in his future endeavours in the cricket media. Ross Perry presents an analysis of Australia's fi rst 16-Test winning streak from October 1999 to March 2001. A future issue of The Yorker will cover their second run of 16 Test victories. We note that part two of Trevor Ruddell's article detailing the development of the rules of Australian football has been delayed until our next issue, which is due around Easter 2010. THE EDITORS Treasures from the Collections The day Don Bradman met his match in Frank Thorn On Saturday, February 25, 1939 a large crowd gathered in the Melbourne District competition throughout the at the Adelaide Oval for the second day’s play in the fi nal 1930s, during which time he captured 266 wickets at 20.20. Sheffi eld Shield match of the season, between South Despite his impressive club record, he played only seven Australia and Victoria. The fans came more in anticipation games for Victoria, in which he captured 24 wickets at an of witnessing the setting of a world record than in support average of 26.83. Remarkably, the two matches in which of the home side, which began the game one point ahead he dismissed Bradman were his only Shield appearances, of its opponent on the Shield table. -

STEVE WAUGH Published 16.3.17 It Was Test Match Cricket That You Couldn't Take Your Eyes Off It Was Predictable but Still Disa
STEVE WAUGH Published 16.3.17 It was Test match cricket that you couldn’t take your eyes off It was predictable but still disappointing that a brilliant Test match in which two sides had to draw upon all their reserves of mental and physical toughness in an old fashioned dogfight that saw conflict, confrontation, skill and tension before a remarkable comeback from the home, was somewhat forgotten in the aftermath of the DRS controversy. That said, I could understand the talk, the speculation and the spin each expert gave on what transpired in Bangalore. After all, the captains involved are two of the most popular and revered figures in the game today. Hopefully, the incident is behind both teams and not still smouldering as they ready themselves for the third Test in Ranchi. I was in Bangalore to witness the first three days of the Test and it was an engrossing game on a difficult pitch where batsmen could get runs if they punished the loose balls and capitalised on moments of good fortune. There was more than enough variable bounce to keep the quick bowlers interested and prodigious turn at times to enable the spinners to dominate. Both teams had their opportunities to seize the momentum but chasing 150 or more in the fourth innings was always going to be a demanding examination for the Australians particularly with Ashwin and Jadeja ready to restrict and then ultimately strangle as would an anaconda its prey. Looking ahead, Australia are in Ranchi for the venue’s debut Test without their strike bowler Mitchell Starc. -

Matador Bbqs One Day Cup Winners “Some Plan B’S Are Smarter Than Others, Don’T Drink and Drive.” NIGHTWATCHMAN NATHAN LYON
Matador BBQs One Day Cup Winners “Some plan b’s are smarter than others, don’t drink and drive.” NIGHTWATCHMAN NATHAN LYON Supporting the nightwatchmen of NSW We thank Cricket NSW for sharing our vision, to help develop and improve road safety across NSW. Our partnership with Cricket NSW continues to extend the Plan B drink driving message and engages the community to make positive transport choices to get home safely after a night out. With the introduction of the Plan B regional Bash, we are now reaching more Cricket fans and delivering the Plan B message in country areas. Transport for NSW look forward to continuing our strong partnership and wish the team the best of luck for the season ahead. Contents 2 Members of the Association 61 Toyota Futures League / NSW Second XI 3 Staff 62 U/19 Male National 4 From the Chairman Championships 6 From the Chief Executive 63 U/18 Female National 8 Strategy for NSW/ACT Championships Cricket 2015/16 64 U/17 Male National 10 Tributes Championships 11 Retirements 65 U/15 Female National Championships 13 The Steve Waugh/Belinda Clark Medal Dinner 66 Commonwealth Bank Australian Country Cricket Championships 14 Australian Representatives – Men’s 67 National Indigenous Championships 16 Australian Representatives – Women’s 68 McDonald’s Sydney Premier Grade – Men’s Competition 17 International Matches Played Lauren Cheatle in NSW 73 McDonald’s Sydney Premier Grade – Women’s Competition 18 NSW Blues Coach’s Report 75 McDonald’s Sydney Shires 19 Sheffield Shield 77 Cricket Performance 24 Sheffield Shield -
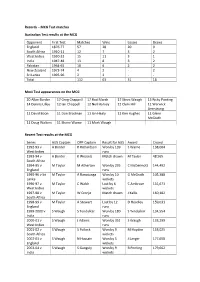
Records – MCG Test Matches Australian Test Results at the MCG
Records – MCG Test matches Australian Test results at the MCG Opponent First Test Matches Wins Losses Draws England 1876-77 57 28 20 9 South Africa 1910-11 12 7 3 2 West Indies 1930-31 15 11 3 1 India 1947-48 13 8 3 2 Pakistan 1964-65 10 6 2 2 New Zealand 1973-74 4 2 - 2 Sri Lanka 1995-96 2 2 - - Total 112 63 31 18 Most Test appearances on the MCG 20 Allan Border 17 Greg Chappell 17 Rod Marsh 17 Steve Waugh 15 Ricky Ponting 14 Dennis Lillee 12 Ian Chappell 12 Neil Harvey 12 Clem Hill 11 Warwick Armstrong 11 David Boon 11 Don Bradman 11 Ian Healy 11 Kim Hughes 11 Glenn McGrath 11 Doug Walters 11 Shane Warne 11 Mark Waugh Recent Test results at the MCG Series AUS Captain OPP Captain Result for AUS Award Crowd 1992-93 v A Border R Richardson Won by 139 S Warne 138,604 West Indies runs 1993-94 v A Border K Wessels Match drawn M Taylor 48,565 South Africa 1994-95 v M Taylor M Atherton Won by 295 C McDermott 144,492 England runs 1995-96 v Sri M Taylor A Ranatunga Won by 10 G McGrath 105,388 Lanka wickets 1996-97 v M Taylor C Walsh Lost by 6 C Ambrose 131,671 West Indies wickets 1997-98 v M Taylor W Cronje Match drawn J Kallis 160,182 South Africa 1998-99 v M Taylor A Stewart Lost by 12 D Headley 159,031 England runs 1999-2000 v S Waugh S Tendulkar Won by 180 S Tendulkar 134,554 India runs 2000-01 v S Waugh J Adams Won by 352 S Waugh 133,299 West Indies runs 2001-02 v S Waugh S Pollock Won by 9 M Hayden 153,025 South Africa wickets 2002-03 v S Waugh N Hussain Won by 5 J Langer 177,658 England wickets 2003-04 v S Waugh S Ganguly Won by 9 R Ponting -

Wisden History
David Dunstan, "Wisden History" David Dunstan WISDEN HISTORY. Captain Cook and cricket caps. The review of the National Museum of Australia, with its heartfelt yearning for the return of great-white-bloke stories, makes for rather vexing reading ..." Great-white-bloke history is bunk. We can do better. The Age 18 July 2003, Ann McGrath, director of the Australian Centre for Indigenous History at the ANU. Retired banker and horse breeder paid $425,000 for Donald Bradman's 1948 baggy green cap. On loan for public display, the cap is to do a tour of duty through Brisbane, Melbourne, Adelaide and Sydney for the 2003104 summer Test series. Source: Museum bags taxing piece of hi story The Australian 10 September 2003. As if the oval were the wide world, we wait squinting with the gulls through the soft, suntan haze at the distant, lazy middle where the ball is bowled, blocked. Soon Steve Waugh in the baggy green will make the news with a lift of the red ball up over the barmy army into the cloudless blue. Today success is all but guaranteed by the sweep and crack of cricket history, the triumphant Aussie book of Wisden. 1 When Steve and team step on to the hallowed ground wearing the traditional baggy green, they walk beside the legends of Chappell, Miller and Bradman and together they warm the stands, the bars and every last esky on the hill with the promise of still more glory. 58 Volume 31, number 1, May 2004 Such is the passion of the times, beyond the oval, across the nation, our libraries and museums have been refurbished in tribute to the wonder of the willow. -

Xref Cricket Catalogue for Auction
Page:1 May 19, 2019 Lot Type Grading Description Est $A SPORTING MEMORABILIA - General & Miscellaneous Lots 4 BADGES: Cricket & Football membership badges c1980-1991, noted Melbourne Cricket Club (9); Essendon (8) & VFL Park (4), mainly fine condition. (21) 100 Lot 5 5 BASEBALL: c1905 real photo postcard of the Victorian Baseball team with some of their partners and 21 signatures including Test Cricketer Frank Laver, also T.Vaughan, W.G.Hickford, S.G.Lansdown, W.J.Scott, extremely scarce and superb condition. 300 8 EPHEMERA: Group including tennis with photographs of Martina Navratilova (8; one signed); 1957 & 1961 Davis Cup programmes; fishing with book "Rod and Stream" by Sharp [London, 1928]; 1892 invoice to Melbourne Cricket Club; c1950 MSD cricket catalogue; 1956 Olympics programmes (3); 1891 programme for Douglas Bay Regatta (Isle of Man). (41) 100 9 FRAMED SPORTING MEMORABILIA: Balance of collection including cricket (39); football with items from Adelaide, Brisbane (2), Carlton (2), Collingwood (6), Essendon (6), Footscray (2), Hawthorn (2), Melbourne, North Melbourne (3), Richmond, StKilda (9) & Swans (2); boxing; golf (3) & horse racing. Buyer must collect. (84) 200 CRICKET - General & Miscellaneous Lots 16 Balance of cricket collection including 1949 Capstan calendar featuring Don Bradman (some faults); 1947 Capstan calendar (damaged); Bradman Centenary calendar; supplement 'Australians Who Played in 1932-3 Test Series'; 1970s programmes/tour guides (13); tea towels (3); newspapers; door stop in shape of bowler. 150 17 Cricket collection including range of 1977 Centenary Test souvenirs; replica urn (repaired); stamps, covers, FDCs & coins; cricket mugs (3); book 'The Art of Bradman'; 1987 cricket medal from Masters Games. -

Executive Summary
EXECUTIVE SUMMARY International club cricket tournament in its 5th year played at the heart of the Singapore Cricket Club and its iconic home ground, The Padang. Opportunity for branding coverage at The Padang through online and print channels such as social media and local/international press respectively. Entertain your clients and staff over two cricket action- packed days in an exclusive marquee catered to by the Singapore Cricket Club catering team. Sponsorship Packages: • Hospitality Sponsorship • Team Sponsorship • And more… 5th SINGAPORE CRICKET CLUB INTERNATIONAL TWENTY20 THE EVENT The Singapore Cricket Club (SCC) International Twenty20 is one of the highest profile cricket tournaments in the region, featuring top international stars representing some of the most famous clubs in the game, to compete over three days of first class competition. Set in the heart of Singapore’s city centre, SCC’s home ground, The Padang, plays host to the event, with a spectacular skyline of the Singapore Central Business District. It is a truly outstanding venue for this highly prestigious occasion, making it truly a memorable event for players and spectators. Clubs in attendance will include Melbourne Cricket Club, Hong Kong Cricket Club, Kowloon Cricket Club, Singhalese Sports Club, Madras Cricket Club and Singapore Cricket Club. 5th SINGAPORE CRICKET CLUB INTERNATIONAL TWENTY20 Since its inception as a professional format for cricket in 2003, Twenty20 cricket has THE STORY shown how a sport with strong tradition can adapt and reinvent itself to fit modern OF consumer habits and tastes. As a format TWENTY20 T20 or short form cricket has been responsible for staggering growth in cricket audiences worldwide. -

A Bayesian Analysis of Early Dismissals in Cricket
Getting Your Eye In: A Bayesian Analysis of Early Dismissals in Cricket Brendon James Brewer School of Mathematics and Statistics The University of New South Wales [email protected] February 17, 2013 Abstract A Bayesian Survival Analysis method is motivated and developed for analysing sequences of scores made by a batsman in test or first class cricket. In particular, we expect the presence of an effect whereby the distribution of scores has more probability near zero than a geometric distribution, due to the fact that batting is more difficult when the batsman is new at the crease. A Metropolis-Hastings algorithm is found to be efficient at estimating the proposed parameters, allowing us to quantify exactly how large this early-innings effect is, and how long a batsman needs to be at the crease in order to “get their eye in”. Applying this model to several modern players shows that a batsman is typically only playing at about half of their potential ability when they first arrive at the crease, and gets their eye in surprisingly quickly. Additionally, some players are more “robust” (have a smaller early-innings effect) than others, which may have implications for selection policy. 1 Introduction It is well known to cricketers of all skill levels that the longer a batsman is in for, the easier batting tends to become. This is probably due to a large number of psychological and technique-related effects: for example, it is generally agreed that it takes a while for a batsman’s footwork to “warm up” and for them to adapt to the subtleties of the prevailing conditions and the bowling attack. -

ADAM GILCHRIST Published on 9.12.17 Playing As an Indivisible
ADAM GILCHRIST Published on 9.12.17 Playing as an indivisible unit the reason behind Australia’s success Perfection, success and triumph are tricky things in a team sport. Personal success is only part of the greater picture, and a perfect, ideal team player is one who enjoys the success of his teammates as much as he does his own. Having been part of a team that won three World Cups and was the number one team in Test cricket, I can say that it was a team of different, diverse individuals. I would even go to the extent of saying that not all the players were fast friends, and yes, there were several superstars in the team as well. However, when we went onto the field, we played as an indivisible unit, and that was the success of the Australian team. We had a truly exceptional motivator in John Buchanan who would challenge us in different ways. He ensured that we never rested on our laurels and was always finding ways of expanding our horizons. Steve Waugh and Ricky Ponting, too, were outstanding leaders and Australia had one streak each, of sixteen wins each, under these two captains. Both were strong personalities and ensured that our motivation never dipped during those winning streaks. It took exceptional performances (coincidentally, it was India on both occasions) to stop our streak. Teamwork also makes the challenge of looking after one’s own performance both a selfish and selfless enterprise. One factoid that gives me immense pleasure is the fact that I have fifty-plus scores in all of the three World Cup finals that I played in. -

The Shield Returns
ISSUE 26 / APR 2014 GO THE SHIELD RETURNS INSIDE Stephen O’Keefe Sarah Aley Ryan Carters Jake Doran Build the perfect partnership. We are proud to be the offi cial Chartered Accountants and Advisors of the NSW Blues and Offi cial Events Partner of Cricket NSW. Call us on 02 9221 2099 email [email protected] or visit www.pitcher.com.au for more information Melbourne | Sydney | Adelaide | Perth | Brisbane | Newcastle Pitcher Partners is an association of independent fi rms. An independent member of Baker Tilly International. GO BLUES APRIL 2014 3 CONTENTS 05 FROM THE CHIEF EXECUTIVE 06 THE SHIELD RETURNS Blues celebrate the Sheffield Shield’s return to NSW 09 THE STEVE WAUGH MEDAL DINNER All the winners from Cricket NSW’s night of nights! 10 UNDER-RATED Stephen O’Keefe was the leading wicket taker in the Sheffield Shield, and deserves higher honours 12 ALEY RETURNS TO THE TOP After a summer on the sideline, Sarah Aley has shown some of her best form for the Lend Lease Breakers 15 NSW BLUES LIFT OUT POSTER Get your poster of the 2013/14 Bupa Sheffield Shield Champions! 19 THE 100 CLUB Cricket NSW celebrates the men and women who have played 100 First Class and WNCL matches for the State 21 CLEAR MIND KEY FOR CARTERS Getting back to nature means getting runs in the middle 24 ALL EYES ON DORAN This teenage wonderkid seems destined for bigger things 29 DREAMS BECOME A REALITY The Adamstown Rosebuds lived the dream of playing the NSW Blues on the SCG thanks to Transport for NSW’s Plan B Game Changer Award Published for Cricket NSW by Proactive