How Nature Produces Blue Color
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(Lepidoptera: Papilionidae) of Kerala Part of Western Ghats Usin
Journal of Entomology and Zoology Studies 2014; 2 (4): 72-77 ISSN 2320-7078 Taxonomic segregation of the Swallowtails of the JEZS 2014; 2 (4): 72-77 © 2014 JEZS genus Graphium (Lepidoptera: Papilionidae) of Received: 23-06-2014 Accepted: 17-07-2014 Kerala part of Western Ghats using morphological V.S. Revathy characters of external genitalia Entomology Department, Forest Health Division, Kerala Forest V.S. Revathy and George Mathew Research Institute, Peechi, Kerala- 680635 Abstract George Mathew Studies on the genitalia of four species of Papilionids belonging to the tribe Leptocercini were made. The Entomology Department, Forest structure of vinculum, uncus, valvae and phallus of the male genitalia and the bursa, ductus and ovipositor Health Division, Kerala Forest of the female were found to be useful in taxonomic segregation of these butterflies. This highlights the Research Institute, Peechi, Kerala- extreme practical importance of external genitalic structures in the identification of these butterflies and 680635 improves upon earlier characters for generic and specific determinations based mainly on the wing venation, size and shape of palpi, and frons. Keywords: Taxonomy, Papilionidae, Lepidoptera, Graphium, Western Ghats 1. Introduction The Western Ghats constitute a mountain range along the western side of India. It is acclaimed as World Heritage Site by UNESCO and is one of the world’s eight “hottest hotspots" of biological diversity. Southern Western Ghats extending from the Agasthamalai to Palghat Gap has highest butterfly diversity with maximum Endemics. Thirty six species of butterflies are reported to be endemic to the Ghat and among the butterfly genera, the genus Parantirrhoea is exclusively [11] endemic to this region . -
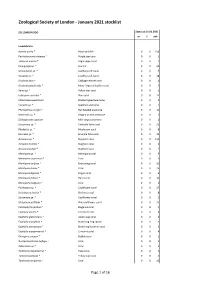
Jan 2021 ZSL Stocklist.Pdf (699.26
Zoological Society of London - January 2021 stocklist ZSL LONDON ZOO Status at 01.01.2021 m f unk Invertebrata Aurelia aurita * Moon jellyfish 0 0 150 Pachyclavularia violacea * Purple star coral 0 0 1 Tubipora musica * Organ-pipe coral 0 0 2 Pinnigorgia sp. * Sea fan 0 0 20 Sarcophyton sp. * Leathery soft coral 0 0 5 Sinularia sp. * Leathery soft coral 0 0 18 Sinularia dura * Cabbage leather coral 0 0 4 Sinularia polydactyla * Many-fingered leather coral 0 0 3 Xenia sp. * Yellow star coral 0 0 1 Heliopora coerulea * Blue coral 0 0 12 Entacmaea quadricolor Bladdertipped anemone 0 0 1 Epicystis sp. * Speckled anemone 0 0 1 Phymanthus crucifer * Red beaded anemone 0 0 11 Heteractis sp. * Elegant armed anemone 0 0 1 Stichodactyla tapetum Mini carpet anemone 0 0 1 Discosoma sp. * Umbrella false coral 0 0 21 Rhodactis sp. * Mushroom coral 0 0 8 Ricordea sp. * Emerald false coral 0 0 19 Acropora sp. * Staghorn coral 0 0 115 Acropora humilis * Staghorn coral 0 0 1 Acropora yongei * Staghorn coral 0 0 2 Montipora sp. * Montipora coral 0 0 5 Montipora capricornis * Coral 0 0 5 Montipora confusa * Encrusting coral 0 0 22 Montipora danae * Coral 0 0 23 Montipora digitata * Finger coral 0 0 6 Montipora foliosa * Hard coral 0 0 10 Montipora hodgsoni * Coral 0 0 2 Pocillopora sp. * Cauliflower coral 0 0 27 Seriatopora hystrix * Bird nest coral 0 0 8 Stylophora sp. * Cauliflower coral 0 0 1 Stylophora pistillata * Pink cauliflower coral 0 0 23 Catalaphyllia jardinei * Elegance coral 0 0 4 Euphyllia ancora * Crescent coral 0 0 4 Euphyllia glabrescens * Joker's cap coral 0 0 2 Euphyllia paradivisa * Branching frog spawn 0 0 3 Euphyllia paraancora * Branching hammer coral 0 0 3 Euphyllia yaeyamaensis * Crescent coral 0 0 4 Plerogyra sinuosa * Bubble coral 0 0 1 Duncanopsammia axifuga + Coral 0 0 2 Tubastraea sp. -

Speciation in Graphium Sarpedon (Linnaeus)
ZOBODAT - www.zobodat.at Zoologisch-Botanische Datenbank/Zoological-Botanical Database Digitale Literatur/Digital Literature Zeitschrift/Journal: Stuttgarter Beiträge Naturkunde Serie A [Biologie] Jahr/Year: 2013 Band/Volume: NS_6_A Autor(en)/Author(s): Page Malcolm G. P., Treadaway Colin G. Artikel/Article: Speciation in Graphium sarpedon (Linnaeus) and allies (Lepidoptera: Rhopalocera: Papilionidae) 223-246 Stuttgarter Beiträge zur Naturkunde A, Neue Serie 6: 223–246; Stuttgart, 30.IV.2013 223 Speciation in Graphium sarpedon (Linnaeus) and allies (Lepidoptera: Rhopalocera: Papilionidae) MALCOLM G. P. PAGE & COLIN G. TREADAWAY Abstract The relationships between subspecies of Graphium sarpedon (Linnaeus, 1758) and closely allied species have been investigated. This group appears to comprise eight sibling species, as follows: Graphium sarpedon (Linnaeus, 1758), G. adonarensis (Rothschild, 1896) stat. rev., G. anthedon (Felder & Felder, 1864), G. milon (Felder & Felder, 1865) stat. rev., G. isander (Godman & Salvin, 1888) stat. rev., G. choredon (Felder & Felder, 1864) stat. rev., G. teredon (Felder & Felder, 1864) stat. rev., G. jugans (Rothschild, 1896) stat. rev. The following new subspecies are described: G. sarpedon sirkari n. subsp. from N. India and S. China, G. adonarensis hundertmarki n. subsp. from Bali, G. adonarensis agusyantoei n. subsp. from Sumatra, G. adonarensis phyrisoides n. subsp. from Bangka and Belitung, G. adonarensis toxopei n. subsp. from Lombok, G. adonarensis septentrionicolus n. subsp. from N. India and E. China. K e y w o r d s : Lepidoptera, Papilionidae, Graphium sarpedon, new subspecies. Zusammenfassung Die Beziehungen zwischen den Unterarten von Graphium sarpedon (Linnaeus, 1758) und anderer nahestehender Arten der Gattung werden untersucht. Diese Gruppe nahe verwandter Arten enthält wahrscheinlich acht Taxa wie folgt: Graphium sarpedon (Linnaeus, 1758), G. -

Two Projects of Butterfly Farming in Cambodia and Tanzania (Insecta: Lepidoptera) SHILAP Revista De Lepidopterología, Vol
SHILAP Revista de Lepidopterología ISSN: 0300-5267 [email protected] Sociedad Hispano-Luso-Americana de Lepidopterología España van der Heyden, T. Local and effective: Two projects of butterfly farming in Cambodia and Tanzania (Insecta: Lepidoptera) SHILAP Revista de Lepidopterología, vol. 39, núm. 155, septiembre, 2011, pp. 267-270 Sociedad Hispano-Luso-Americana de Lepidopterología Madrid, España Available in: http://www.redalyc.org/articulo.oa?id=45522101004 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative 267-270 Local and effective Tw 10/9/11 17:37 Página 267 SHILAP Revta. lepid., 39 (155), septiembre 2011: 267-270 CODEN: SRLPEF ISSN:0300-5267 Local and effective: Two projects of butterfly farming in Cambodia and Tanzania (Insecta: Lepidoptera) T. van der Heyden Abstract The projects “Banteay Srey Butterfly Centre” in Cambodia (Asia) and “Zanzibar Butterfly Centre” in Tanzania (Africa) are presented as models of sustainable butterfly farming to support local communities. KEY WORDS: Insecta, Lepidoptera, butterfly farming, sustainability, conservation, development, tropics, Cambodia, Tanzania. Local y efectivo: Dos proyectos de cría de mariposas en Camboya y Tanzania (Insecta: Lepidoptera) Resumen Los proyectos “Banteay Srey Butterfly Centre” en Camboya (Asia) y “Zanzibar Butterfly Centre” in Tanzania -

1968 a TAXONOMIC LIST of PHILATELIC LEPIDOPTERA Many
1968 Journal of the Lepidopterists' Society 241 A TAXONOMIC LIST OF PHILATELIC LEPIDOPTERA SIDNEY A. HESSEL Peabody Museum of Natural History, Yale University, New Haven, Conn. Many lepidopterists are also philatelists. This includes professional entomologists, some of whom are those actually responsible as insti gators or consultants for the many butterfly and moth postage stamps that have of late years appeared around the world. The first philatelic lepidopteran was issued in 1890 as an ornament in the hair of Hawaiian Queen Liliuokalani. Although one may speculate that it is the beautiful Vanessa tameamea Esch., it was not until 1930 when Lebanon honored the silk industry that a definitely determinable species was depicted. Stylized figures had appeared in the interval. In these instances the insects were, of course, incidental. Sarawak in 1950 was the first with nomenclature, Troides brookiana Wallace, which was figured unicolorous gray. It remained for the Swiss Pro Juventute issue of 1950 to honor the insect exclusively and in full color. This was largely the work of Dr. Loeliger, a member of our Society until his death and an important force in the Pro Juventute youth movement. The issue was accompanied by a brochure about the insects and was a most noteworthy effort towards stimulation of interest in Lepidoptera in that country. From this beginning, at first slowly, but with accelerated frequency, over 65 countries have "honored" species of Lepidoptera by 310 butterfly and 115 moth stamps, a total of 425 major varieties by the end of 1966. These embrace 248 species divided 181 and 67 respectively between butterflies and moths. -

On the Presence of Graphium Doson Felder & Felder
Journal of Entomology and Zoology Studies 2014; 2 (2): 111-114 ISSN 2320-7078 On the presence of Graphium doson Felder & JEZS 2014; 2 (2): 111-114 © 2014 JEZS Felder (Lepidoptera: Rhopalocera) in plains of Received: 12-03-2014 Accepted: 25-04-2014 Punjab with notes on its life history Charn Kumar Department of Biology, A.S. College Charn Kumar and Rajandeep Singh Samrala Road Khanna, Punjab-141 401, India. Email: [email protected] ABSTRACT Rajandeep Singh The Common Jay, Graphium doson Felder & Felder belonging to family Papilionidae has been reported Department of Biology, A.S. College first time from the plains of Punjab in Khanna and Bathinda. As per the earlier checklists from the state, Samrala Road Khanna, Punjab-141 the species is unreported from the plains in Punjab. This seems to be a recent range extension of the 401, India. species from foothills to the plains. Different stages of life history of Graphium doson have been observed Email: [email protected] on Polyalthia longifolia var. pendula (False Ashoka Tree) belonging to family Annonaceae. The plant is largely grown as an avenue tree in the residential colonies and institutions. Observations on egg laying, larval feeding, growth and pupation of this butterfly have been made. Keywords: Butterflies, Punjab, Graphium, Polyalthia, Instar. 1. Introduction The Common jay, Graphium doson Felder & Felder is widely distributed in China, Sunda Islands, South India, Sri Lanka, Burma, Assam Hills and the Himalaya upto Kumaon [1, 2, 3, 4, 5]. Out of the 14 subspecies found within its distribution range, two subspecies namely, the Himalyan Common Jay, Graphium doson axion Felder & Felder and the Dakhan Common Jay Graphium doson eleius Felder & Felder are recognized in India. -

University of Groningen Butterfly Wing Colors Stavenga, Doekele G
University of Groningen Butterfly wing colors Stavenga, Doekele G.; Giraldo, Marco A.; Leertouwer, Hein L. Published in: Journal of Experimental Biology DOI: 10.1242/jeb.041434 IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please check the document version below. Document Version Publisher's PDF, also known as Version of record Publication date: 2010 Link to publication in University of Groningen/UMCG research database Citation for published version (APA): Stavenga, D. G., Giraldo, M. A., & Leertouwer, H. L. (2010). Butterfly wing colors: glass scales of Graphium sarpedon cause polarized iridescence and enhance blue/green pigment coloration of the wing membrane. Journal of Experimental Biology, 213(10), 1731-1739. https://doi.org/10.1242/jeb.041434 Copyright Other than for strictly personal use, it is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license (like Creative Commons). The publication may also be distributed here under the terms of Article 25fa of the Dutch Copyright Act, indicated by the “Taverne” license. More information can be found on the University of Groningen website: https://www.rug.nl/library/open-access/self-archiving-pure/taverne- amendment. Take-down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Downloaded from the University of Groningen/UMCG research database (Pure): http://www.rug.nl/research/portal. -

Catalogue of Swallowtail Butterflies (Lepidoptera: Papilionidae) at BORNEENSIS
Catalogue of Swallowtail Butterflies (Lepidoptera: Papilionidae) at BORNEENSIS Compiled by: AKINORI NAKANISHI, MOHD. FAIRUS JALIL & NORDIN WAHID Photographs by: AKINORI NAKANISHI & AZRIE ALLIAMAT BBEC Publication No. 24 First Printed 2004 ISBN 983-3108-04-0 Catalogue of Swallowtail Butterflies (Lepidoptera: Papilionidae) at BORNEENSIS Compiled by Akinori Nakanishi, Mohd. Fairus Jalil, & Nordin Wahid Copyright © 2004 Institute for Tropical Biology & Conservation, UMS Editors: Akinori Nakanishi (JICA expert / Hyogo Museum) Mohd. Fairus Jalil (Tutor in ITBC, UMS) Nordin Wahid (Assistant in ITBC, UMS) Published by Research & Education Component, Bornean Biodiversity and Ecosystem Conservation (BBEC) Programme in Sabah c/o Institute for Tropical Biology & Conservation (ITBC) Universiti Malaysia Sabah Locked Bag 2073 88999, Kota Kinabalu Sabah, Malaysia Design and layout by Mohd. Fairus Jalil & Akinori Nakanishi Cover page: Papilio (Princeps) demolion Catalogue of Swallowtail Butterflies (Lepidoptera: Papilionidae) at BORNEENSIS Compiled by: AKINORI NAKANISHI, MOHD. FAIRUS JALIL & NORDIN WAHID Photographs by: AKINORI NAKANISHI & AZRIE ALLIAMAT Foreward The Institute for Tropical Biology and Conservation, Universiti Malaysia Sabah, has a reference collection center called BORNEENSIS. Under the Bornean Biodiversity and Ecosystem Conservation (BBEC) programme, we hope to establish it to be a center form taxonomy and systematic studies for Bornean fauna and flora of the region. In line with this effort we produced records of what is kept at BORNEENSIS, and this book is one. At the same time this small book will act as a guide for those involved with conservation, including students, staff, rangers and naturalists. As we all know butterfly has always been of interest to many people, we hope it will be useful to you too. -

MICROSTRUCTURE of BLUE/GREEN and YELLOW PIGMENTED WING MEMBRANES in LEPIDOPTERA with Remarks Concerning the Function of Pterobilins 1
BULLETIN OF THE ALLYN MUSEUM 3701 Bayshore Rd. Sarasota, Florida 33580 Published By The Florida State Museum University of Florida Gainesville. Florida 32611 Number...75 15 October 1982 MICROSTRUCTURE OF BLUE/GREEN AND YELLOW PIGMENTED WING MEMBRANES IN LEPIDOPTERA With Remarks Concerning the Function of Pterobilins 1. Genus Graphium A. C. ALLYN Allyn Museum of Entomology MIRIAM ROTHSCHILD Ashton Wold, Peterborough D. S. SMITH Department of Zoology, Oxford University. and the Hope Entomological Collections INTRODUCTION Relatively few studies have been made on the structure of the coloured wing membranes which, if they are not obscured by the presence of overlying scales, can play an impor tant role in the visual patterns of butterflies. We have here concentrated on the modifications associated with such exposed coloured membranes in selected species of the genus Graphium. In this group of swallowtails there are large areas of both hind- and forewings which are bright blue and blue-green in col our, occasionally yellow and in one instance mauve and green - but are devoid of the usual type of wing-scale covering and thus afford and excellent opportunity for examining the microstructure and pigmentation of the wing membranes themselves. Studies of other genera with similar modified structures will be the subject of a conti nuing series of publications. MATERIALS AND METHODS Reflectance and absorbance were measured on a Beckman (DB-GTj grating spec trophotometer using a 10° specular reflectance accessory and a beam attenuation of 92%. The samples were charted using a Beckman lO-inch recorder in a continuous readout from 190 nm to 700 nm. -

The Papilionidae (Lepidoptera): Co-Evolution with the Angiosperms
©Verlag Ferdinand Berger & Söhne Ges.m.b.H., Horn, Austria, download unter www.biologiezentrum.at Phyton (Austria) Vol. 23 Fasc. 1 117-126 15. 2. 1983 The Papilionidae (Lepidoptera): Co-evolution with the Angiosperms Denis RICHARD*) and Michel With 2 figures Received March 8, 1982 Key words: Butterflies, Papilionidae. — Angiospermae, Asterales, Magnoliales, Rutales, Umbellales. — Co-evolution, evolution Summary RICHARD D. & GUEDES M. 1983. The Papilionidae (Lepidoptera): co- evolution with the Angiosperms. — Phyton (Austria) 23 (1): 117—126, 2 fi- gures. — English with German summary. The Papilionidae appears to have co-evolved with two lines of Angiosperms, the one rooted in the Magnoliales or rather their ancestors, the other in the Rosales-Myrtales or their ancestors. The Papilionini (Graphiini) is especially interesting in being adapted to a lineage including the Magnoliales, Rutales, Umbellales and Asterales, whose existence is clear on phytochemical and morpho- logical grounds. It is stressed that morphological differentiation does not go necessarily hand in hand with adaptive co-evolution: whereas the whole of the Troidini remained adapted to the Aristolochiaceae, the single genus Papilio (Papilionini) "learned" to feed on a succession of related families culminating in the Gompositae, and still remained unchanged at even the genus level. Zusammenfassung RICHARD D. & GTTEDES M. 1983. Die Papilionidae (Lepidoptera): Coevo- lution mit den Angiospermen. — Phyton (Austria) 23 (1): 117 — 126, 2 Abbil- dungen. — Englisch mit deutscher Zusammenfassung. Die Papilionidae haben anscheinend mit zwei Linien der Angiospermen coevolviert, nämlich mit einer, die im Bereich der Magnoliales oder eher ihrer *) Denis RICHARD, Laboratoire de Matiere medicale, U. E. R. de Pharma- cie, Poitiers, France. -

Swallowtails of the World
Swallowtails of the World Papilio natewa A pictorial review of the Papilionidae by Richard I Vane-Wright & N. Mark Collins Swallowtails are insects – invertebrate animals with three pairs of jointed legs Papilio (Princeps) demoleus Swallowtails belong to the Lepidoptera – insects that undergo complete metamorphosis and have four broad wings covered in scales There are: • About 185,000 named species of Lepidoptera (moths and butterflies) • About 18,500 species of Papilionoidea (butterflies and skippers) divided between seven families • Almost 600 species in the family There are three swallowtail subfamilies: Papilionidae • Baroniinae: one species • Parnassiinae: 65+ species • Papilioninae: 500++ species Some characteristics of swallowtails The osmeterium is the swallowtail caterpillar’s defensive scent-gland – a unique structure found in all species for which the larvae are known The chrysalis is attached by a silk base-pad – the cremaster, and a silk girdle (except Parnassius) Wing venation: Forewing vein 2A is separate The subfamily Baroniinae includes just a single species from Mexico – Baronia brevicornis The Parnassiinae – only found in the northern hemisphere – are usually divided among seven genera Archon apollinus – one of two species of the genus Archon Hypermnestra helios – the only species in the genus Fifty or more species belong to the genus Parnassius – this is Parnasssius eversmanni, placed by some specialists in subgenus Driopa, one of about six subgroups often recognised Parnassius (Parnassius) apollo – the famous Apollo Butterfly, pictured here from the Val d'Aosta, Italy Bhutanitis lidderdalii – one of the four remarkable species belonging to this genus Luehdorfia japonica– one of four species in the genus Sericinus montela – the only species of this graceful swallowtail genus Zerynthia rumina – one of seven species in this colourful parnassiine genus The majority of swallowtails belong This is to the third major subgroup – the Eurytides Papilioninae. -

A New Species of Graphium Scopoli (Lepidoptera: Papilionidae) from the Bismarck Archipelago, Papua New Guinea
© Copyright Australian Museum, 1999 Records of the Australian Museum (1999) Vol. 51: 161–168. ISSN 0067-1975 A New Species of Graphium Scopoli (Lepidoptera: Papilionidae) from the Bismarck Archipelago, Papua New Guinea C.J. MÜLLER 1 AND W.J. TENNENT 2 1 Address for correspondence: P.O. Box 228, Dural NSW 2158, Australia 1 Centre for Ore Deposit Research, University of Tasmania, GPO Box 252-79, Hobart TAS 7001, Australia [email protected] 2 Biogeography and Conservation Laboratory, Department of Entomology, The Natural History Museum, Cromwell Road, London SW7 5BD, England ABSTRACT. Graphium kosii n.sp., a butterfly from high elevations in southern New Ireland, is described and figured. A key is presented for this and five closely related species: Graphium weiskei (Ribbe), G. stresemanni (Rothschild), G. batjanensis Okano, G. macleayanum (Leach) and G. gelon (Boisduval), all of which are confined to the Australasian region. MÜLLER, C.J., & W.J. TENNENT, 1999. A new species of Graphium Scopoli (Lepidoptera: Papilionidae) from the Bismarck Archipelago, Papua New Guinea. Records of the Australian Museum 51(2): 161–168. This paper is the first of two treating new butterflies from Valley as World Heritage during 1992–1996 but terminated little known montane forests of New Ireland. It describes a the project due to “land ownership difficulties” (P. Lavender, new species of Graphium. New Ireland is a long (c. 400 Pacific Heritage Foundation, pers. comm., 1998). km) ancient island arc situated northeast of New Britain The “weiskei” group of butterflies within the genus (2°–4°S 151°–153°E). The highest land reaches 2399 m in Graphium comprises six closely related species: G.