DOCSLIB.ORG

Thermodynamics and Statistical Mechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermodynamics and Statistical Mechanics Camille Bélanger-ChampagneLuis Anchordoqui LehmanMcGill College University City University of New York ThermodynamicsCharged Particle and StatisticalCorrelations Mechanics in Minimum Bias Events at ATLAS • Thermodynamic● Physics motivation potentials Enthalpy • ● Minbias event and track selection Thermodynamics IV Helmholtz free energy th • ● Azimuthal correlation results 18 SeptemberFebruary 2014 26 2012,• Gibbs free energy WNPPC 2012 • Chemical● Forward-Backward potential correlation results • Landau free energy Thursday, September 18, 14 1 THERMODYNAMIC POTENTIALS Thermodynamic systems may do work on their environments Under certain constraintsOverview ☛ work done may be bounded from above by change in appropriately defined thermodynamic potential Imagine creating thermodynamic system from scratch in thermally insulated box of volume V Work to assemble system ☛ = U W After bringing together all particles from infinity system has internal energy U System however ☛ may not be in thermal equilibrium Spontaneous processes will then occur so as to maximize system’s entropy but internal energy remains @ U dU = δQ δW ☛ U(S, V ) First Law − Combining Main thermodynamics identity dU = TdS PdV − @U @U it follows that T = and P = { @S V − @V S ✓ ◆ ✓ ◆ Second Law in form δQ TdS yields ☛ dU TdS PdV − C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 2 FREE WORK For porcess @ fixed ☛ (S, V ) dU 0 Overview) This says spontaneous processes in system with dS = dV =0 always lead to reduction of internal energy In systems @ fixed (S, V ) spontaneous processes drive internal energy U to a minimum Allowing for other work processes ☛ δW TdS dU − Work done by system under thermodynamic conditions of constant entropy is bounded above by dU and maximum δ W is achieved− for reversible processes It is useful to define ☛ δW = δW PdV free − which is differential work done by system other than required to change V It follows that ☛ δW TdS PdV dU free − − CONCLUSION: for systems @ fixed ( S, V ) ☛ δ W dU free C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 3 THE LEGENDRE TRANSFORMATION Consider function Z =Overview Z ( x, y ) and compute differential dZ(x, y)=Xdx + Ydy (A) x, X and y, Y are (by definition) canonically conjugate pairs To replace (x, y) by ( X, Y ) as independent variables transform Z = Z ( x, y ) according to M(X, Y )=Z xX yY − − it follows that ☛ dM = dZ Xdx Ydy xdX ydY (B) − − − − Substituting (A) into (B) ☛ dM = xdX ydY (C) − − (A) and (C) give reciprocity relations: @Z @Z @M @M = X, = Y, = x, = y @x @y @X − @Y − C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 4 THE LEGENDRE TRANSFORMATION II To replace only one Overviewof the variables tansform according to N(x, Y )=Z yY (D) − it follows that dN = dZ Ydy ydY (E) − − Substituting (A) into (E) ☛ dN = Xdx ydY − with reciprocity relations: @N @N = X, = Y @x @y − C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 5 THE LEGENDRE TRANSFORMATION III Curve in a plane can Overviewbe equally represented by: pairs of coordinates (point geometry) envelope of a family of tangent lines (line geometry) Z y C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 6 THE LEGENDRE TRANSFORMATION IV Overview For given Z = Z ( y ) consider tangent line that goes through point (y, Z) and has slope dZ/dy = Y If Z intercept is N ☛ equation of line is given by (D) Z N Y = − N = Z yY y 0 ) − − it follows that ☛ dN = dZ ydY Ydy − − but ☛ dZ = Ydy dN = ydY dN ) − which is reciprocal relation ☛ y = − dY Legendre transformation is mapping from ( y, Z ) space to ( Y,N ) space ☛ point representation of curve into tangent line representation C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 7 ENTHALPY Suppose ☛ we spontaneouslyOverview create system while it is thermally insulated but in constant mechanical contact with “volume bath” @ pressure P = U + PV W quantity U + PV ☛ enthalpy Legendre transformation with respect to pairs of variables P, V H = U + PV (123) so that in equilibrium ☛ dH = dU + PdV + VdP Enthalpy should be considered as a function of S and P that are its native variables ☛ dH = TdS + VdP (124) @H @H It follows that ☛ T = and V = (125) @S @P !P !S @T @V = (126) and Maxwell relation ☛ @P @S !S !P C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 8 ENTHALPY II Overview In general we have ☛ dH TdS + VdP In systems @ fixed (S, P ) spontaneous processes drive enthalpy H to a minimum For general systems dH TdS δW + PdV + VdP − δW TdS + VdP dH free − CONCLUSION: for systems @ fixed ( S, P ) ☛ δ W dH free C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 9 HELMHOLTZ FREE ENERGY Suppose ☛ we spontaneously create system while it is in contact Overviewwith thermal reservoir at temperature T = U TS W − quantity U TS ☛ Helmholtz free energy Legendre transformation− with respect to pairs of variables T, S F = U TS (127) − so that in equilibrium ☛ dF = dU TdS SdT − − F should be considered as a function of T and V that are its native variables ☛ dF = SdT PdV (128) − − @F @F It follows that ☛ S = and P = (129) − @T − @V !V !T @S @P = and Maxwell relation ☛ @V @T (130) !T !V C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 10 HELMHOLTZ FREE ENERGY II Overview In general the Second Law tells us ☛ dF SdT PdV − Equality holds for reversible processes and inequality for spontaneous processes In systems @ fixed (T,V ) spontaneous processes drive Helmholtz free energy F to a minimum We may also write work done by a thermodynamic system under conditions of constant T is bounded above by dF and− maximum δ W is achieved for reversible processes δW SdT PdV dF free − − CONCLUSION: for systems @ fixed ( T,V ) ☛ δ W dF free C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 11 GIBBS FREE ENERGY If we create thermodynamicOverview system at conditions of constant T it absorbs heat energy Q = TS from reservoir and we must expend work energy PV in order to make room for it = U TS + PV Gibbs free energy is obtainedW by a second− Legendre transformation G = U TS + PV (131) − For equilibrium systems dG = SdT + VdP − (132) so that G = G ( T,P ) in native variables @G @G (133) It follows that ☛ S = and V = − @T @P !P !T @S @V and Maxwell relation ☛ = (134) − @P @T !T !P C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 12 GIBBS FREE ENERGY II Second Law says thatOverview dG SdT + VdP In systems @ fixed (T,P) spontaneous processes drive Gibbs free energy G to a minimum For general systems δW SdT + VdP dG free − CONCLUSION: for systems @ fixed ( T,P ) ☛ δ W dG free C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 13 HOMEWORK ON THERMODYNAMIC POTENTIALS For given F ☛ obtain:Overview entropy from (129) @F internal energy U = F + TS = F T (135) − @T !V @S @2F heat capacity CV = T = T @T − @T2 (136) !V !V Show that for perfect gas ☛ combination of (58), (127), (115) yields γ 1 F = C T + U C T ln (TV − ) TS (137) V 0 − V − 0 Check that (135) and (136) yield familiar results for perfect gas From (129) with the use of (50) obtain equation of state @F C T (γ 1) nRT P = = V − = (138) − @V V V !T C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 14 OPEN SYSTEMS Mass of system was Overviewconsidered as constant and dropped from arguments of thermodynamic functions If system can exchange mass with environment or there are chemical reactions in system masses of components change and can cause change of other quantities If mass is added to system with a constant volume pressure typically increases Throughout we will consider number of particles N instead of mass or number of kilomoles n Connection between N and n has been given in (6) Using N is preferable in statistical physics while n is more convenient in chemistry C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 15 CHEMICAL POTENTIAL With account of massOverview changes ☛ internal energy becomes , U = U(S, V, N) and main thermodynamic identity (84) should be modified accordingly dU = TdS PdV + µdN (139) − ☟ @U µ = chemical potential per particle ☛ @N (140) !S,V Chemical potential per kilomole ☛ substitute last term in (139) by µdn For multicomponent system such as mixture of different gases described by numbers of particles N i ☛ µdN µ dN ) i i i X C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 16 EULER’S THEOREM Since all arguments in OverviewU ( S, V, N ) are extensive quantities multiplying them all by a parameter λ means simply increasing whole system by λ that leads to increase of U by λ Mathematically ☛ for any function f this property can be expressed as λf(x, y, z)=f(λx, λy,λz) (141) Differentiate (141) with respect to λ and then set λ =1 to obtain @f @f @f f = x + y + z (142) @x @y @z Applying Euler’s theorem @U @U m @U U = S + V + nj @S @V @nj ✓ ◆V,ni ✓ ◆S,ni j=1 ✓ ◆S,V,ni From the differential of U : X @U @U @U = T, = P, = µj @S @V − @nj ✓ ◆V,ni ✓ ◆S,ni ✓ ◆S,V,ni C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14 17 GIBBS-DUHEM RELATION So that one obtains ☛ U = TS PV + µN (143) Overview− Using definition of Gibbs free energy (131) we rewrite this relation in the form ☛ G = µN (144) ☟ Chemical potential is Gibbs free energy per particle For open systems ☛ differentials of thermodynamic potentials become: (124), (128), (132) dH = TdS + VdP + µdN (145) dF = SdT PdV + µdN (146) − − (147) dG = SdT + VdP + µdN − From (144) follows ☛ dG = µdN + Ndµ (148) which combined with (147) yields the Gibbs-Duhem equation SdT VdP + Ndµ =0 (149) − C.Luis B.-Champagne Anchordoqui 2 Thursday, September 18, 14
Load more

Recommended publications
  • Chapter 3. Second and Third Law of Thermodynamics
    Chapter 3. Second and third law of thermodynamics Important Concepts Review Entropy; Gibbs Free Energy • Entropy (S) – definitions Law of Corresponding States (ch 1 notes) • Entropy changes in reversible and Reduced pressure, temperatures, volumes irreversible processes • Entropy of mixing of ideal gases • 2nd law of thermodynamics • 3rd law of thermodynamics Math • Free energy Numerical integration by computer • Maxwell relations (Trapezoidal integration • Dependence of free energy on P, V, T https://en.wikipedia.org/wiki/Trapezoidal_rule) • Thermodynamic functions of mixtures Properties of partial differential equations • Partial molar quantities and chemical Rules for inequalities potential Major Concept Review • Adiabats vs. isotherms p1V1 p2V2 • Sign convention for work and heat w done on c=C /R vm system, q supplied to system : + p1V1 p2V2 =Cp/CV w done by system, q removed from system : c c V1T1 V2T2 - • Joule-Thomson expansion (DH=0); • State variables depend on final & initial state; not Joule-Thomson coefficient, inversion path. temperature • Reversible change occurs in series of equilibrium V states T TT V P p • Adiabatic q = 0; Isothermal DT = 0 H CP • Equations of state for enthalpy, H and internal • Formation reaction; enthalpies of energy, U reaction, Hess’s Law; other changes D rxn H iD f Hi i T D rxn H Drxn Href DrxnCpdT Tref • Calorimetry Spontaneous and Nonspontaneous Changes First Law: when one form of energy is converted to another, the total energy in universe is conserved. • Does not give any other restriction on a process • But many processes have a natural direction Examples • gas expands into a vacuum; not the reverse • can burn paper; can't unburn paper • heat never flows spontaneously from cold to hot These changes are called nonspontaneous changes.
    [Show full text]
  • Thermodynamics, Flame Temperature and Equilibrium
    Thermodynamics, Flame Temperature and Equilibrium Combustion Summer School 2018 Prof. Dr.-Ing. Heinz Pitsch Course Overview Part I: Fundamentals and Laminar Flames • Introduction • Fundamentals and mass balances of combustion systems • Thermodynamic quantities • Thermodynamics, flame • Flame temperature at complete temperature, and equilibrium conversion • Governing equations • Chemical equilibrium • Laminar premixed flames: Kinematics and burning velocity • Laminar premixed flames: Flame structure • Laminar diffusion flames • FlameMaster flame calculator 2 Thermodynamic Quantities First law of thermodynamics - balance between different forms of energy • Change of specific internal energy: du specific work due to volumetric changes: δw = -pdv , v=1/ρ specific heat transfer from the surroundings: δq • Related quantities specific enthalpy (general definition): specific enthalpy for an ideal gas: • Energy balance for a closed system: 3 Multicomponent system • Specific internal energy and specific enthalpy of mixtures • Relation between internal energy and enthalpy of single species 4 Multicomponent system • Ideal gas u and h only function of temperature • If cpi is specific heat at constant pressure and hi,ref is reference enthalpy at reference temperature Tref , temperature dependence of partial specific enthalpy is given by • Reference temperature may be arbitrarily chosen, most frequently used: Tref = 0 K or Tref = 298.15 K 5 Multicomponent system • Partial molar enthalpy hi,m is and its temperature dependence is where the molar specific
    [Show full text]
  • Thermodynamics
    ME346A Introduction to Statistical Mechanics { Wei Cai { Stanford University { Win 2011 Handout 6. Thermodynamics January 26, 2011 Contents 1 Laws of thermodynamics 2 1.1 The zeroth law . .3 1.2 The first law . .4 1.3 The second law . .5 1.3.1 Efficiency of Carnot engine . .5 1.3.2 Alternative statements of the second law . .7 1.4 The third law . .8 2 Mathematics of thermodynamics 9 2.1 Equation of state . .9 2.2 Gibbs-Duhem relation . 11 2.2.1 Homogeneous function . 11 2.2.2 Virial theorem / Euler theorem . 12 2.3 Maxwell relations . 13 2.4 Legendre transform . 15 2.5 Thermodynamic potentials . 16 3 Worked examples 21 3.1 Thermodynamic potentials and Maxwell's relation . 21 3.2 Properties of ideal gas . 24 3.3 Gas expansion . 28 4 Irreversible processes 32 4.1 Entropy and irreversibility . 32 4.2 Variational statement of second law . 32 1 In the 1st lecture, we will discuss the concepts of thermodynamics, namely its 4 laws. The most important concepts are the second law and the notion of Entropy. (reading assignment: Reif x 3.10, 3.11) In the 2nd lecture, We will discuss the mathematics of thermodynamics, i.e. the machinery to make quantitative predictions. We will deal with partial derivatives and Legendre transforms. (reading assignment: Reif x 4.1-4.7, 5.1-5.12) 1 Laws of thermodynamics Thermodynamics is a branch of science connected with the nature of heat and its conver- sion to mechanical, electrical and chemical energy. (The Webster pocket dictionary defines, Thermodynamics: physics of heat.) Historically, it grew out of efforts to construct more efficient heat engines | devices for ex- tracting useful work from expanding hot gases (http://www.answers.com/thermodynamics).
    [Show full text]
  • Grand-Canonical Ensemble
    PHYS4006: Thermal and Statistical Physics Lecture Notes (Unit - IV) Open System: Grand-canonical Ensemble Dr. Neelabh Srivastava (Assistant Professor) Department of Physics Programme: M.Sc. Physics Mahatma Gandhi Central University Semester: 2nd Motihari-845401, Bihar E-mail: [email protected] • In microcanonical ensemble, each system contains same fixed energy as well as same number of particles. Hence, the system dealt within this ensemble is a closed isolated system. • With microcanonical ensemble, we can not deal with the systems that are kept in contact with a heat reservoir at a given temperature. 2 • In canonical ensemble, the condition of constant energy is relaxed and the system is allowed to exchange energy but not the particles with the system, i.e. those systems which are not isolated but are in contact with a heat reservoir. • This model could not be applied to those processes in which number of particle varies, i.e. chemical process, nuclear reactions (where particles are created and destroyed) and quantum process. 3 • So, for the method of ensemble to be applicable to such processes where number of particles as well as energy of the system changes, it is necessary to relax the condition of fixed number of particles. 4 • Such an ensemble where both the energy as well as number of particles can be exchanged with the heat reservoir is called Grand Canonical Ensemble. • In canonical ensemble, T, V and N are independent variables. Whereas, in grand canonical ensemble, the system is described by its temperature (T),volume (V) and chemical potential (μ). 5 • Since, the system is not isolated, its microstates are not equally probable.
    [Show full text]
  • The Grand Canonical Ensemble
    University of Central Arkansas The Grand Canonical Ensemble Stephen R. Addison Directory ² Table of Contents ² Begin Article Copyright °c 2001 [email protected] Last Revision Date: April 10, 2001 Version 0.1 Table of Contents 1. Systems with Variable Particle Numbers 2. Review of the Ensembles 2.1. Microcanonical Ensemble 2.2. Canonical Ensemble 2.3. Grand Canonical Ensemble 3. Average Values on the Grand Canonical Ensemble 3.1. Average Number of Particles in a System 4. The Grand Canonical Ensemble and Thermodynamics 5. Legendre Transforms 5.1. Legendre Transforms for two variables 5.2. Helmholtz Free Energy as a Legendre Transform 6. Legendre Transforms and the Grand Canonical Ensem- ble 7. Solving Problems on the Grand Canonical Ensemble Section 1: Systems with Variable Particle Numbers 3 1. Systems with Variable Particle Numbers We have developed an expression for the partition function of an ideal gas. Toc JJ II J I Back J Doc Doc I Section 2: Review of the Ensembles 4 2. Review of the Ensembles 2.1. Microcanonical Ensemble The system is isolated. This is the ¯rst bridge or route between mechanics and thermodynamics, it is called the adiabatic bridge. E; V; N are ¯xed S = k ln ­(E; V; N) Toc JJ II J I Back J Doc Doc I Section 2: Review of the Ensembles 5 2.2. Canonical Ensemble System in contact with a heat bath. This is the second bridge between mechanics and thermodynamics, it is called the isothermal bridge. This bridge is more elegant and more easily crossed. T; V; N ¯xed, E fluctuates.
    [Show full text]
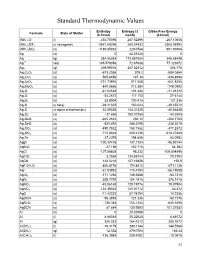
  • Standard Thermodynamic Values
    Standard Thermodynamic Values Enthalpy Entropy (J Gibbs Free Energy Formula State of Matter (kJ/mol) mol/K) (kJ/mol) (NH4)2O (l) -430.70096 267.52496 -267.10656 (NH4)2SiF6 (s hexagonal) -2681.69296 280.24432 -2365.54992 (NH4)2SO4 (s) -1180.85032 220.0784 -901.90304 Ag (s) 0 42.55128 0 Ag (g) 284.55384 172.887064 245.68448 Ag+1 (aq) 105.579056 72.67608 77.123672 Ag2 (g) 409.99016 257.02312 358.778 Ag2C2O4 (s) -673.2056 209.2 -584.0864 Ag2CO3 (s) -505.8456 167.36 -436.8096 Ag2CrO4 (s) -731.73976 217.568 -641.8256 Ag2MoO4 (s) -840.5656 213.384 -748.0992 Ag2O (s) -31.04528 121.336 -11.21312 Ag2O2 (s) -24.2672 117.152 27.6144 Ag2O3 (s) 33.8904 100.416 121.336 Ag2S (s beta) -29.41352 150.624 -39.45512 Ag2S (s alpha orthorhombic) -32.59336 144.01328 -40.66848 Ag2Se (s) -37.656 150.70768 -44.3504 Ag2SeO3 (s) -365.2632 230.12 -304.1768 Ag2SeO4 (s) -420.492 248.5296 -334.3016 Ag2SO3 (s) -490.7832 158.1552 -411.2872 Ag2SO4 (s) -715.8824 200.4136 -618.47888 Ag2Te (s) -37.2376 154.808 43.0952 AgBr (s) -100.37416 107.1104 -96.90144 AgBrO3 (s) -27.196 152.716 54.392 AgCl (s) -127.06808 96.232 -109.804896 AgClO2 (s) 8.7864 134.55744 75.7304 AgCN (s) 146.0216 107.19408 156.9 AgF•2H2O (s) -800.8176 174.8912 -671.1136 AgI (s) -61.83952 115.4784 -66.19088 AgIO3 (s) -171.1256 149.3688 -93.7216 AgN3 (s) 308.7792 104.1816 376.1416 AgNO2 (s) -45.06168 128.19776 19.07904 AgNO3 (s) -124.39032 140.91712 -33.472 AgO (s) -11.42232 57.78104 14.2256 AgOCN (s) -95.3952 121.336 -58.1576 AgReO4 (s) -736.384 153.1344 -635.5496 AgSCN (s) 87.864 130.9592 101.37832 Al (s)
    [Show full text]
  • Energy and Enthalpy Thermodynamics
    Energy and Energy and Enthalpy Thermodynamics The internal energy (E) of a system consists of The energy change of a reaction the kinetic energy of all the particles (related to is measured at constant temperature) plus the potential energy of volume (in a bomb interaction between the particles and within the calorimeter). particles (eg bonding). We can only measure the change in energy of the system (units = J or Nm). More conveniently reactions are performed at constant Energy pressure which measures enthalpy change, ∆H. initial state final state ∆H ~ ∆E for most reactions we study. final state initial state ∆H < 0 exothermic reaction Energy "lost" to surroundings Energy "gained" from surroundings ∆H > 0 endothermic reaction < 0 > 0 2 o Enthalpy of formation, fH Hess’s Law o Hess's Law: The heat change in any reaction is the The standard enthalpy of formation, fH , is the change in enthalpy when one mole of a substance is formed from same whether the reaction takes place in one step or its elements under a standard pressure of 1 atm. several steps, i.e. the overall energy change of a reaction is independent of the route taken. The heat of formation of any element in its standard state is defined as zero. o The standard enthalpy of reaction, H , is the sum of the enthalpy of the products minus the sum of the enthalpy of the reactants. Start End o o o H = prod nfH - react nfH 3 4 Example Application – energy foods! Calculate Ho for CH (g) + 2O (g) CO (g) + 2H O(l) Do you get more energy from the metabolism of 1.0 g of sugar or
    [Show full text]
  • Calculation of Chemical Potential and Activity Coefficient of Two Layers of Co2 Adsorbed on a Graphite Surface
    Physical Chemistry Chemical Physics CALCULATION OF CHEMICAL POTENTIAL AND ACTIVITY COEFFICIENT OF TWO LAYERS OF CO2 ADSORBED ON A GRAPHITE SURFACE Journal: Physical Chemistry Chemical Physics Manuscript ID: CP-ART-08-2014-003782.R1 Article Type: Paper Date Submitted by the Author: 07-Nov-2014 Complete List of Authors: Trinh, Thuat; NTNU, Department of Chemistry Bedeaux, Dick; NTNU, Chemistry Simon, Jean-Marc; Universit� de Bourgogne, Chemistry Kjelstrup, Signe; Norwegian University of Science and Technology, Natural Sciences Page 1 of 8 Physical Chemistry Chemical Physics PCCP RSC Publishing ARTICLE CALCULATION OF CHEMICAL POTENTIAL AND ACTIVITY COEFFICIENT OF TWO LAYERS Cite this: DOI: 10.1039/x0xx00000x OF CO2 ADSORBED ON A GRAPHITE SURFACE T.T. Trinh,a D. Bedeaux a , J.-M Simon b and S. Kjelstrup a,c,* Received 00th January 2014, Accepted 00th January 2014 We study the adsorption of carbon dioxide at a graphite surface using the new Small System DOI: 10.1039/x0xx00000x Method, and find that for the temperature range between 300K and 550K most relevant for CO separation; adsorption takes place in two distinct thermodynamic layers defined according www.rsc.org/ 2 to Gibbs. We calculate the chemical potential, activity coefficient in both layers directly from the simulations. Based on thermodynamic relations, the entropy and enthalpy of the CO 2 adsorbed layers are also obtained. Their values indicate that there is a trade-off between entropy and enthalpy when a molecule chooses for one of the two layers. The first layer is a densely packed monolayer of relatively constant excess density with relatively large repulsive interactions and negative enthalpy.
    [Show full text]
  • Chapter 4 Solution Theory
    SMA5101 Thermodynamics of Materials Ceder 2001 Chapter 4 Solution Theory In the first chapters we dealt primarily with closed systems for which only heat and work is transferred between the system and the environment. In the this chapter, we study the thermodynamics of systems that can also exchange matter with other systems or with the environment, and in particular, systems with more than one component. First we focus on homogeneous systems called solutions. Next we consider heterogeneous systems with emphasis on the equilibrium between different multi-component phases. 4.1 WHAT IS A SOLUTION? A solution in thermodynamics refers to a system with more than one chemical component that is mixed homogeneously at the molecular level. A well-known example of a solution is salt water: The Na+, Cl- and H2O ions are intimately mixed at the atomic level. Many systems can be characterized as a dispersion of one phase within another phase. Although such systems typically contain more than one chemical component, they do not form a solution. Solutions are not limited to liquids: for example air, a mixture of predominantly N2 and O2, forms a vapor solution. Solid solutions such as the solid phase in the Si-Ge system are also common. Figure 4.1. schematically illustrates a binary solid solution and a binary liquid solution at the atomic level. Figure 4.1: (a) The (111) plane of the fcc lattice showing a cut of a binary A-B solid solution whereby A atoms (empty circles) are uniformly mixed with B atoms (filled circles) on the atomic level.
    [Show full text]
  • Chemistry 130 Gibbs Free Energy
    Chemistry 130 Gibbs Free Energy Dr. John F. C. Turner 409 Buehler Hall [email protected] Chemistry 130 Equilibrium and energy So far in chemistry 130, and in Chemistry 120, we have described chemical reactions thermodynamically by using U - the change in internal energy, U, which involves heat transferring in or out of the system only or H - the change in enthalpy, H, which involves heat transfers in and out of the system as well as changes in work. U applies at constant volume, where as H applies at constant pressure. Chemistry 130 Equilibrium and energy When chemical systems change, either physically through melting, evaporation, freezing or some other physical process variables (V, P, T) or chemically by reaction variables (ni) they move to a point of equilibrium by either exothermic or endothermic processes. Characterizing the change as exothermic or endothermic does not tell us whether the change is spontaneous or not. Both endothermic and exothermic processes are seen to occur spontaneously. Chemistry 130 Equilibrium and energy Our descriptions of reactions and other chemical changes are on the basis of exothermicity or endothermicity ± whether H is negative or positive H is negative ± exothermic H is positive ± endothermic As a description of changes in heat content and work, these are adequate but they do not describe whether a process is spontaneous or not. There are endothermic processes that are spontaneous ± evaporation of water, the dissolution of ammonium chloride in water, the melting of ice and so on. We need a thermodynamic description of spontaneous processes in order to fully describe a chemical system Chemistry 130 Equilibrium and energy A spontaneous process is one that takes place without any influence external to the system.
    [Show full text]
  • Lecture 13. Thermodynamic Potentials (Ch
    Lecture 13. Thermodynamic Potentials (Ch. 5) So far, we have been using the total internal energy U and, sometimes, the enthalpy H to characterize various macroscopic systems. These functions are called the thermodynamic potentials: all the thermodynamic properties of the system can be found by taking partial derivatives of the TP. For each TP, a set of so-called “natural variables” exists: −= + μ NddVPSdTUd = + + μ NddPVSdTHd Today we’ll introduce the other two thermodynamic potentials: theHelmhotzfree energy F and Gibbs free energy G. Depending on the type of a process, one of these four thermodynamic potentials provides the most convenient description (and is tabulated). All four functions have units of energy. When considering different types of Potential Variables processes, we will be interested in two main U (S,V,N) S, V, N issues: H (S,P,N) S, P, N what determines the stability of a system and how the system evolves towards an F (T,V,N) V, T, N equilibrium; G (T,P,N) P, T, N how much work can be extracted from a system. Diffusive Equilibrium and Chemical Potential For completeness, let’s rcall what we’vee learned about the chemical potential. 1 P μ d U T d= S− P+ μ dVd d= S Nd U +dV d − N T T T The meaning of the partial derivative (∂S/∂N)U,V : let’s fix VA and VB (the membrane’s position is fixed), but U , V , S U , V , S A A A B B B assume that the membrane becomes permeable for gas molecules (exchange of both U and N between the sub- ns ilesystems, the molecuA and B are the same ).
    [Show full text]
  • Thermodynamic Potentials and Thermodynamic Relations In
    arXiv:1004.0337 Thermodynamic potentials and Thermodynamic Relations in Nonextensive Thermodynamics Guo Lina, Du Jiulin Department of Physics, School of Science, Tianjin University, Tianjin 300072, China Abstract The generalized Gibbs free energy and enthalpy is derived in the framework of nonextensive thermodynamics by using the so-called physical temperature and the physical pressure. Some thermodynamical relations are studied by considering the difference between the physical temperature and the inverse of Lagrange multiplier. The thermodynamical relation between the heat capacities at a constant volume and at a constant pressure is obtained using the generalized thermodynamical potential, which is found to be different from the traditional one in Gibbs thermodynamics. But, the expressions for the heat capacities using the generalized thermodynamical potentials are unchanged. PACS: 05.70.-a; 05.20.-y; 05.90.+m Keywords: Nonextensive thermodynamics; The generalized thermodynamical relations 1. Introduction In the traditional thermodynamics, there are several fundamental thermodynamic potentials, such as internal energy U , Helmholtz free energy F , enthalpy H , Gibbs free energyG . Each of them is a function of temperature T , pressure P and volume V . They and their thermodynamical relations constitute the basis of classical thermodynamics. Recently, nonextensive thermo-statitstics has attracted significent interests and has obtained wide applications to so many interesting fields, such as astrophysics [2, 1 3], real gases [4], plasma [5], nuclear reactions [6] and so on. Especially, one has been studying the problems whether the thermodynamic potentials and their thermo- dynamic relations in nonextensive thermodynamics are the same as those in the classical thermodynamics [7, 8]. In this paper, under the framework of nonextensive thermodynamics, we study the generalized Gibbs free energy Gq in section 2, the heat capacity at constant volume CVq and heat capacity at constant pressure CPq in section 3, and the generalized enthalpy H q in Sec.4.
    [Show full text]