31 Indian Mathematicians
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Saga of Indian Scientists
BOOK Review scientists, all of them were born before Independence, 25 of them in the 19th century. Hoariest among them is our spirited THE SAGA OF nationalist mathematician, Radhanath Sikdar, famous for measuring the height of Mt. Everest. He is also ‘one of the earliest pioneers of popular science writing in the country’. INDIAN SCIENTISTS He was born in 1813. By Vinod Varshney Most of these scientists were exposed to western scientific culture and conducted some of their important research, if not all, in the well-equipped labs abroad, but their mission had always been to develop science and technology in India. Treading in the footsteps of their seniors, the younger lot too resolutely took upon themselves to grapple with post- independence challenges to promote scientific and technological capabilities constrained with meagre infrastructural resources. They indeed laid a credible foundation of the much-needed science and technology base in the country which has today mushroomed into over 5,000 labs where approximately 5 lakh scientists work. The bio-sketches have been written by seasoned science writers and journalists who have deployed their ingenuity in presenting multiple facets of their scientific work, thinking and personality and also events that helped mould their outlook. But this has been done in a tiny space – only three pages per scientist. In such a niggardly space they could not have satiated readers’ hunger to know the complete complex scenario which existed in their time and blow by blow account of their vision Title: INDIAN SCIENTISTS and spirit. THE SAGA OF INSPIRED MINDS Most bio-piece scribblers have attempted to explore the Author: Biman Basu, Sukanya Datta, heart, soul and time of the scientists, making them pleasurable T.V. -

A Journey to the Scientific World
A Journey to the Scientific World Ramesh C. Samanta JSPS post doctoral Fellow Chubu University, Japan June 15, 2016 India: Geographical Location and Description Total Area: 32,87,364 km2 (No. 7 in the world) Population: 1,251,695,584 (2015, No. 2 in the world) Capital: New Delhi Time Zone (IST): GMT + 5.30 hrs Number of States and Union Territories: 29 States and 7 Union Territories India: Languages and Religions In the history India has experienced several great civilizations in different part of it and they had different languages. This resulted several different languages: Majority from Indo Aryan civilization, Dravid civilization. Major Languages: Hindi and English Official Languages: Total 23 languages with countless dialect India is well known for its diversity of religious beliefs and practices. All the major religions of the world like Hinduism, Sikhism, Buddhism, Jainism, Islam and Christianity are found and practiced in India with complete freedom Weather in India Extreme climate of being tropical country !!! Hot summer (Temperature goes up to 50 oC) Windy monsoon (average rainfall 1000 mm per year) Pleasant Autumn Snowy winter in Northan part of India Indian Food Indian Spices Indian Curry North Indian Food South Indian Food Tourist Attractions in India Taj Mahal, Agra The Ganges, Varanasi Victoria memorial Hall , Kolkata Sea Beach, Goa India’s Great Personalities Netaji Subhas Jawaaharlal Rabindranath Mahatma Gandhi Chandra Bose Nehru Tagore Swami Sarojini Naidu Vivekananda B. R. Ambedkar Sri Aurobindo Indian Nobel Laureates Rabindranath Tagore C. V. Raman Har Gobind Khorana Nobel Prize in Nobel Prize in Physics, 1930 Nobel Prize in Medicine, Literature, 1913 1968 Mother Teresa Venkatraman Ramakrishnan Kailash Satyarthi Nobel Peace Prize 1979 Nobel Prize in chemistry 2009 Nobel Peace Prize 2014 Indian Scientists Sir Jagadish Chandra Bose (1858-1937): Known for pioneering investigation of radio and microwave optics and plant biology. -

Rationale of the Chakravala Process of Jayadeva and Bhaskara Ii
HISTORIA MATHEMATICA 2 (1975) , 167-184 RATIONALE OF THE CHAKRAVALA PROCESS OF JAYADEVA AND BHASKARA II BY CLAS-OLOF SELENIUS UNIVERSITY OF UPPSALA SUMMARIES The old Indian chakravala method for solving the Bhaskara-Pell equation or varga-prakrti x 2- Dy 2 = 1 is investigated and explained in detail. Previous mis- conceptions are corrected, for example that chakravgla, the short cut method bhavana included, corresponds to the quick-method of Fermat. The chakravala process corresponds to a half-regular best approximating algorithm of minimal length which has several deep minimization properties. The periodically appearing quantities (jyestha-mfila, kanistha-mfila, ksepaka, kuttak~ra, etc.) are correctly understood only with the new theory. Den fornindiska metoden cakravala att l~sa Bhaskara- Pell-ekvationen eller varga-prakrti x 2 - Dy 2 = 1 detaljunders~ks och f~rklaras h~r. Tidigare missuppfatt- 0 ningar r~ttas, sasom att cakravala, genv~gsmetoden bhavana inbegripen, motsvarade Fermats snabbmetod. Cakravalaprocessen motsvarar en halvregelbunden b~st- approximerande algoritm av minimal l~ngd med flera djupt liggande minimeringsegenskaper. De periodvis upptr~dande storheterna (jyestha-m~la, kanistha-mula, ksepaka, kuttakara, os~) blir forstaellga0. 0 . f~rst genom den nya teorin. Die alte indische Methode cakrav~la zur Lbsung der Bhaskara-Pell-Gleichung oder varga-prakrti x 2 - Dy 2 = 1 wird hier im einzelnen untersucht und erkl~rt. Fr~here Missverst~ndnisse werden aufgekl~rt, z.B. dass cakrav~la, einschliesslich der Richtwegmethode bhavana, der Fermat- schen Schnellmethode entspreche. Der cakravala-Prozess entspricht einem halbregelm~ssigen bestapproximierenden Algorithmus von minimaler L~nge und mit mehreren tief- liegenden Minimierungseigenschaften. Die periodisch auftretenden Quantit~ten (jyestha-mfila, kanistha-mfila, ksepaka, kuttak~ra, usw.) werden erst durch die neue Theorie verst~ndlich. -

Crowdsourcing
CROWDSOURCING The establishment of the ZerOrigIndia Foundation is predicated on a single premise, namely, that our decades-long studies indicate that there are sound reasons to assume that facilitating further independent scientific research into the origin of the zero digit as numeral may lead to theoretical insights and practical innovations equal to or perhaps even exceeding the revolutionary progress to which the historic emergence of the zero digit in India somewhere between 200 BCE and 500 CE has led across the planet, in the fields of mathematics, science and technology since its first emergence. No one to date can doubt the astounding utility of the tenth and last digit to complete the decimal system, yet the origin of the zero digit is shrouded in mystery to this day. It is high time, therefore, that a systematic and concerted effort is undertaken by a multidisciplinary team of experts to unearth any extant evidence bearing on the origin of the zero digit in India. The ZerOrigIndia Foundation is intended to serve as instrument to collect the requisite funds to finance said independent scientific research in a timely and effective manner. Research Academics and researchers worldwide are invited to join our efforts to unearth any extant evidence of the zero digit in India. The ZerOrigIndia Foundation will facilitate the research in various ways, chief among which is to engage in fundraising to finance projects related to our objective. Academics and researchers associated with reputed institutions of higher learning are invited to monitor progress reported by ZerOrigIndia Foundation, make suggestions and/or propose their own research projects to achieve the avowed aim. -

Stamps of India - Commemorative by Prem Pues Kumar [email protected] 9029057890
E-Book - 26. Checklist - Stamps of India - Commemorative By Prem Pues Kumar [email protected] 9029057890 For HOBBY PROMOTION E-BOOKS SERIES - 26. FREE DISTRIBUTION ONLY DO NOT ALTER ANY DATA ISBN - 1st Edition Year - 1st May 2020 [email protected] Prem Pues Kumar 9029057890 Page 1 of 76 Nos. YEAR PRICE NAME Mint FDC B. 1 2 3 1947 1 21-Nov-47 31/2a National Flag 2 15-Dec-47 11/2a Ashoka Lion Capital 3 15-Dec-47 12a Aircraft 1948 4 29-May-48 12a Air India International 5 15-Aug-48 11/2a Mahatma Gandhi 6 15-Aug-48 31/2a Mahatma Gandhi 7 15-Aug-48 12a Mahatma Gandhi 8 15-Aug-48 10r Mahatma Gandhi 1949 9 10-Oct-49 9 Pies 75th Anni. of Universal Postal Union 10 10-Oct-49 2a -do- 11 10-Oct-49 31/2a -do- 12 10-Oct-49 12a -do- 1950 13 26-Jan-50 2a Inauguration of Republic of India- Rejoicing crowds 14 26-Jan-50 31/2a Quill, Ink-well & Verse 15 26-Jan-50 4a Corn and plough 16 26-Jan-50 12a Charkha and cloth 1951 17 13-Jan-51 2a Geological Survey of India 18 04-Mar-51 2a First Asian Games 19 04-Mar-51 12a -do- 1952 20 01-Oct-52 9 Pies Saints and poets - Kabir 21 01-Oct-52 1a Saints and poets - Tulsidas 22 01-Oct-52 2a Saints and poets - MiraBai 23 01-Oct-52 4a Saints and poets - Surdas 24 01-Oct-52 41/2a Saints and poets - Mirza Galib 25 01-Oct-52 12a Saints and poets - Rabindranath Tagore 1953 26 16-Apr-53 2a Railway Centenary 27 02-Oct-53 2a Conquest of Everest 28 02-Oct-53 14a -do- 29 01-Nov-53 2a Telegraph Centenary 30 01-Nov-53 12a -do- 1954 31 01-Oct-54 1a Stamp Centenary - Runner, Camel and Bullock Cart 32 01-Oct-54 2a Stamp Centenary -
CDA WEB UPDATE.Xlsx
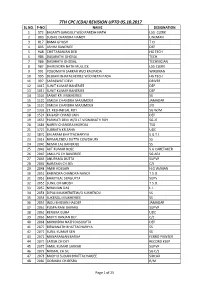
7TH CPC (CDA) REVISION UPTO 05.10.2017 SL.NO.P-NO NAME DESIGNATION 1 572 BASANTI GANGULY W/O PARESH NATH LSG CLERK 2 803 SUSHIL CHANDRA NANDY LINEMAN 3 817 RAMA GHOSH T.O. 4 895 ASHIM BANERJEE DEP 5 948 CHITTARANJAN DEB HG TECH 6 986 DASARATHI GHOSAL TECH 7 986 DASARATH GHOSAL TECHNICIAN 8 987 DHIRENDRA NATH MULLICK LSG CLERK 9 991 YOGOMAYA SARKAR W/O KALIPADA WIREMAN 10 995 DEBJANI BHATACHERJEE W/O NETAI PADA HG TECH 11 997 SARASWATI DEVI DRIVER 12 1017 SUNIT KUMAR BANERJEE DEP 13 1017 SUNIT KUMAR BANERJEE DEP 14 1107 SANAT KR. MUKHERJEE SS 15 1120 UMESH CHANDRA MAJUMDER JAMADAR 16 1120 UMESH CHANDRA MAJUMDER J/D 17 1332 LT. KESHAB LAL ROY SG W/M 18 1524 KAILASH CHAND JAIN DEP 19 1655 PARWATI DEVI W/O LT.VISWANATH ROY SG.JE 20 1686 NAREN CHANDRA MONDAL TSO 21 1727 SUBRATA KR.SAHA UDC 22 1870 BALARAM BHATTACHARYYA S.G.T.I. 23 2016 NIRMALENDU DUTTA COWDHURY SS 24 2040 NEMAI LAL BANERJEE SS 25 2042 AJIT KUMAR BOSE S.G CARETAKER 26 2043 AMULYA CH BANERJEE SG.AEA 27 2045 ANUPAMA DUTTA SUPVR 28 2046 NARAYAN CH SEN C/J 29 2048 AMIR HOSSAIN H.G W/MAN 30 2052 RABINDRA CHANDRA NANDY T.S.O. 31 2053 BHAKTILAL SENGUPTA SUPV 32 2055 SUNIL CH GHOSH T.S.O. 33 2057 NIRANJAN DAS L.I. 34 2058 DIPALI MUKHERJEEW/O SUKHENDU SS 35 2058 SUKENDU MUKHERJEE SS 36 2059 INDU BHUSAN HALDER JAMADAR 37 2063 PUSPA RANI BAIRAGI SUPVR 38 2065 RENUKA GUHA UDC 39 2066 MUKTI RANJAN DEY C/S 40 2068 MANINDRA NATH DASGUPTA DEP 41 2070 BISWANATH BHATTACHARYYA SS 42 2071 SUNIL KUMAR SEN SS 43 2072 MANARANJAN BARUA FERRO PRINTER 44 2073 SATISH CH DEY RECORD KEEP 45 2075 AMAL KUMAR SARKAR SUPVR 46 2076 NIRMAL CH SIL SG C/S 47 2078 MADHU SUDAN BHATTACHARJEE SIRCAR 48 2080 GOBINDA CH BESRA R/M Page 1 of 25 SL.NO.P-NO NAME DESIGNATION 49 2083 SUSHIL KR GHOSH C.O. -

Purnangshu Kumar Roy and the S.N. Bose Tradition in Theoretical Physics by Charles Wesley Ervin Email: Wes [email protected] August, 2016
Purnangshu Kumar Roy and the S.N. Bose Tradition in Theoretical Physics By Charles Wesley Ervin Email: [email protected] August, 2016 INTRODUCTION This year Calcutta University marks a historic mile- stone. One hundred years ago the university started teaching physics courses at the newly created College of Science and Technology. Three of the most brilliant Indian physicists of the twentieth century began their careers there. C.V. Raman, the first Palit Professor of Physics, was awarded the Nobel Prize in 1930 for his work on light scattering. The two young lecturers, Meghnad Saha and Satyendra Nath Bose, made major breakthroughs even sooner – Saha in 1920 for deriving the equation that accounts for the spectral classifica- tion of stars and Bose in 1924 for inventing the statisti- cal model that validated Einstein’s hypothesis of light quanta (the Bose Statistics). But this “golden age” of Calcutta physics was P. K. Roy (right) with Satyendra Nath Bose in London, short-lived. Saha went to Allahabad University in March, 1958. Roy studied theoretical physics with Bose for 1923, Bose decamped to Dacca University in 1924, ten years at Calcutta University and then earned his PhD at and Raman left in 1932 to become the first Indian di- Imperial College under Abdus Salam. This photo was taken when Bose came to London to be inducted Fellow of the rector of the Indian Institute of Science in Bangalore. Royal Society. Courtesy of Anjana Srivastava. After the war, however, there was something of a re- naissance. Bose returned in 1945 and gathered a team of talented research workers in the Physics Depart- ment and the Khaira Lab. -

Equation Solving in Indian Mathematics
U.U.D.M. Project Report 2018:27 Equation Solving in Indian Mathematics Rania Al Homsi Examensarbete i matematik, 15 hp Handledare: Veronica Crispin Quinonez Examinator: Martin Herschend Juni 2018 Department of Mathematics Uppsala University Equation Solving in Indian Mathematics Rania Al Homsi “We owe a lot to the ancient Indians teaching us how to count. Without which most modern scientific discoveries would have been impossible” Albert Einstein Sammanfattning Matematik i antika och medeltida Indien har påverkat utvecklingen av modern matematik signifi- kant. Vissa människor vet de matematiska prestationer som har sitt urspring i Indien och har haft djupgående inverkan på matematiska världen, medan andra gör det inte. Ekvationer var ett av de områden som indiska lärda var mycket intresserade av. Vad är de viktigaste indiska bidrag i mate- matik? Hur kunde de indiska matematikerna lösa matematiska problem samt ekvationer? Indiska matematiker uppfann geniala metoder för att hitta lösningar för ekvationer av första graden med en eller flera okända. De studerade också ekvationer av andra graden och hittade heltalslösningar för dem. Denna uppsats presenterar en litteraturstudie om indisk matematik. Den ger en kort översyn om ma- tematikens historia i Indien under många hundra år och handlar om de olika indiska metoderna för att lösa olika typer av ekvationer. Uppsatsen kommer att delas in i fyra avsnitt: 1) Kvadratisk och kubisk extraktion av Aryabhata 2) Kuttaka av Aryabhata för att lösa den linjära ekvationen på formen 푐 = 푎푥 + 푏푦 3) Bhavana-metoden av Brahmagupta för att lösa kvadratisk ekvation på formen 퐷푥2 + 1 = 푦2 4) Chakravala-metoden som är en annan metod av Bhaskara och Jayadeva för att lösa kvadratisk ekvation 퐷푥2 + 1 = 푦2. -

IB ACIO 2014-15 Solved Question Paper
IB ACIO 2014-15 Solved Question Paper 1. Curcuma longa is the scientific name of which spice? A. Cumin B. Cloves C. Turmeric D. Coriander Answer: C 2. Bones found in the hands and feet as the percentage of total number of bones in the body of an adult human being is nearly equal to A. 20% B. 30% C. 40% D. 50% Answer: D 3. Europeans are believed to have brought potatoes to India in the 18th century. Which region of the world is believed to be the origin of potato cultivation? A. Eastern Ghana B. Southern Peru C. Portugal SPLessons D. West Indies Answer: A 4. Oymyakon is generally considered the coldest inhabited area on Earth. Which country Oymyakon is located . A. Mongolia B. Russia C. Greenland D. Iceland Answer: B 5. Which gland in the human body is also known as the third eye A. Pineal B. Pituitary C. Mammary D. Tear gland Answer: A 6. Leukaemia is a group of cancers that usually begins it the bone marrow and results in high numbers of which abnormal cells A. White blood cells B. Red blood cells C. Platelets D. All of these Answer: A SPLessons 7. During an earthquake, two places ‘A’ and ‘B’ record its intensity in Richter scale as 4.0 and 6.0 respectively. IN absolute terms, the ratio of intensity of the earthquake at ‘A’ to that of ‘B’ is: A. 2:3 B. 7:8 C. 141:173 D. 1:100 Answer: D 8. On a cool day in January, the temperature at a place fell below the freezing point and was recorded as -40° Centigrade. -

From Jantar-Mantar to Kavalur
Registered with the Registrar of Newspapers of India: RN.70269/98 ISSN: 0972-169X Monthly Newsletter of Vigyan Prasar December 15, 1999 Vol. 2 No.3 VP News Inside SCIENCE VIDEOS FROM VIGYAN PRASAR Coverage of science in Indian mass media, especially television, has been very poor. One reason, often heard in media circles, is the absence of a Editorial mechanism to cover stories of latest R&D developments from the science and technology institutions in the country. To bridge the gap between Mass media and R&D institutions, Vigyan Prasar has recently launched a science video Prasanta Chandra feature service on experimental basis. Mahalanobis Six feature stories have been produced last month. Three features on National Bureau of Plant Genetic Resources and three on latest developments from the National Physical Laboratory, New Delhi. The feature stories cover From Jantar-Mantar the profile of the largest gene bank in the world - the NBPGR, various Ex-situ techniques to conserve seeds and a report on the plant quarantine division. to Kavalur The stories from NPL cover the 'Teleclock' service to transmit Time Data digitally through a telephone line, the SODAR - Sound Detection and flanging technique for air pollution management and the piezoelectric Accelerometer The Story of Wool PL-810 to measure vibrations. R&D organizations may write to us for covering interesting Research and Development works happening in their laboratories. Delhi's Water and Solid Waste Management: Emerging Scenario Vigyan Prasar has launched a series on India's Environmental Hotspots. The latest publication in this series is on Delhi's water and waste management scenario. -

FINAL Avantika Student Handbook
Student Handbook 2017-18 Do not go where the path may lead, go instead where there is no path and leave a trail. -Ralph Waldo Emerson Welcome to Avantika It was Bob Dylan who said, “People seldom do what they believe in. They do what is convenient, then repent”. To live a life full of bygone opportunities is a life full of misery. To seek comfort in convenience is a crime. By stepping into Avantika, you have entered a vibrant, cosmopolitan campus comprising an eclectic mix of minds from all over the country and beyond; of all political persuasions and socio-economic statuses. You are now an integral part of a residential community of learners with a common goal – that of intellectual transformation. The world as it stands today is replete with challenges – from the contentious presidential contest in America to the refugee crisis in Europe; to climate-related famine in Africa and the drought in California. It’s easy to be overwhelmed by the intensity – as one should be – but let’s not forget, you are a part of the solution. At Avantika, you have the freedom to pursue reason, facts, logic, and empathize with human nature. You will be armed to become the capstone of education by being a conscientious explorer, creator, and thinker. Indeed, the world is now your oyster. Welcome to Avantika. Welcome to a world of opportunities! Contents Know Avantika 01-04 About Us Vision MIT Pune Student Enrollment Reaching Avantika Academics @ Avantika 05-21 Programs Academic Calendar Academic Structure - UG Foundation - UG Academic Structure - PG Foundation - PG Pedagogies What you should bring Life @ Avantika 22-28 Scholarships Code of Conduct Anti-Ragging Policy Hostel Amenities and Rules Mess Rules Disciplinary Procedures and Rules Interesting facts on Ujjain 29-33 Important Contact Details About Avantika Vision At Avantika University, the liberal approach to learning is the one which empowers individuals to deal with complexity, diversity, Avantika aims to and change. -

ARYABHATA-I: an Early Indian Mathematician and His Work
et International Journal on Emerging Technologies (Special Issue NCETST-2017) 8(1): 764-767(2017) (Published by Research Trend, Website: www.researchtrend.net ) ISSN No. (Print) : 0975-8364 ISSN No. (Online) : 2249-3255 ARYABHATA-I: An early Indian Mathematician and his work Govind Singh Assistant Professor-Amrapali Institute of Technology & Sciences, Haldwani (UK) INDIA ABSTRACT: The knowledge of History of early Indian Mathematics prior to 499 CE is not perfect and sufficient. In this paper we explore work done on mathematics by Arya Bhata-I and summarized in his book Arya Bhateeya. Key Words: Arya Bhata-I, Arya Bhateeya, summarized. These two parts are named as Dasageetika and I. INTRODUCTION Ary āshtashatam respectively. On the other hand Arya Kusuma Pura was the older name of Pataliputra Bhata himself gave only a single name to his complete situated in the Magadha state of ancient time, now a work, which was Arya Bhateeya . The second part i.e., place near the modern Patna in Bihar. Aryabhata-I was Ary āshtashatam again ramified as Ganita or one of the Mathematicians and Astronomers those mathematics, Kāla Kriya or the calculation of time and belonged to the Kusuma Pura School of learning, but it the Gōla or sphere. The last two parts deal with the is believed that he was a native of Kerala, a region of astronomical calculations and the first part, which south India. It is due the facts that, the calendar based consists of thirty three verses of the purely upon the systems given in the astronomical work of mathematical importance. Probably Aryabhata-I was Aryabhata-I have been followed to some extent in the first Indian astronomer who gave the value of Kerala even in the modern time.