DOCSLIB.ORG

Second Lecture: Modern Atoms and the Electromagnetic Interaction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Second Lecture: Modern Atoms and the Electromagnetic Interaction HC 209H: Discovery of Fundamental Particles and Interactions Second Lecture: Modern Atoms and the Electromagnetic Interaction Chris Potter University of Oregon HC 209H: Second Lecture – p.1/10 Electrostatic Force and the Planetary Atom Isaac Newton (1642-1727), an English mathematician and physicist, formulated the classical laws of motion and gravity. He also invented (with Leibniz) Calculus. Newton’s law of gravity: the attractive gravitational force between masses m1 and m2, separated by a distance r, is (G is a constant) = × m1×m2 Fg G r2 Charles-Augustin de Coulomb (1736-1806), a French physicist, formulated the law of electrostatic attraction. Coulomb’s electrostatic law: the attractive or repulsive electrostatic force between electric charges q1 and q2, separated by a distance r, is (k is a constant) = × q1×q2 Fe k r2 Planets in our solar system are held in orbit around the sun by gravity. In the planetary atom, negatively Charles-Augustin de Coulomb by charged electrons are held in orbit around a positively Louis Hierle (Credit: Wikipedia) charged nucleus by electrostatic attraction. HC 209H: Second Lecture – p.2/10 Light as an Electromagnetic Wave James Clerk Maxwell (1831-1879), a Scottish physicist, formulated the unified laws of electric fields E~ and magnetic fields B~ . ∇· E~ = 0 ∇· B~ = 0 ∇× ~ − ∂B~ E = ∂t ∇× ~ 1 ∂E~ B = c2 ∂t James Clerk Maxwell, Engraving (Credit: Wikipedia) Changing magnetic fields B~ induce electric fields E~ , and changing electric fields E~ induce magnetic fields B~ : this is light. The wavelength λ and time frequency ν are related to Credits: Wikimedia Commons (top), the speed of light by c = λν. Encyclopedia Brittanica (bottom) HC 209H: Second Lecture – p.3/10 Light as a Particle, the Photon γ Max Planck (1858-1947), a German physicist, first modeled blackbody radiation in 1900 by assuming light exists discrete energy packets, E = hν = hc/λ. Blackbody spectrum (Credit: Encyclopedia Brittanica) Albert Einstein (1879-1955), a German-American physicist, explained in 1910 the photoelectric effect with photons, in which light shining on matter yields electron emission if the frequency ν > E/h. So which is it, is light a wave or a particle? Answer: Albert Einstein ca 1922 (Credit: both. This is the quantum wave/particle duality. Wikipedia) HC 209H: Second Lecture – p.4/10 Subatomic Particles: Electron, Proton, Neutron The modern atom cannot by the atom of the Early Greek philosophers, which was indivisible. What we call an atom is made of protons, neutrons and electrons and is therefore divisible. The Atomic Number Z and Atomic Weight A from Mendeleev’s Peridic Table of the Elements tell us how many protons are in the nucleus: Z protons and A − Z neutrons. Cavendish Laboratory Staff, 1933 All three particles were discovered by physicists at the Cavendish Lab, Cambridge University. The electron (e−) was discovered in 1898 by J.J. Thompson, an English physicist in the cathode ray tube. The nucleus was discovered in 1911 by Ernest Rutherford (with Geiger and Marsden at Manchester), a physicist from New Zealand. The neutron (n) was discovered in 1932 by James Chadwick, an English physicist. HC 209H: Second Lecture – p.5/10 The Bohr Atom, or Quantum Mechanics Problem: the hydrogen planetary atom is unstable. Solution: quantum mechanics. Niels Bohr (1885-1962), a Danish physicist, successfully modelled the light emission spectra of hydrogen assuming that the electron angular momentum is quantized. Bohr assumed (1913) angular momentum L = rmv is quantized, L = n × h/2π (n = 1, 2, 3, 4,...), and set the centripetal force equal to the Coulomb force, e×e = m×v2 k r2 r Solving, he obtains quantized energies and orbits: 2 En = E1/n 2 rn = n × r1 λ = hc/∆E n=1,2,3,. Niels Bohr (Credit: Wikipedia) HC 209H: Second Lecture – p.6/10 The Neutrino: A Desperate Remedy In beta decay of an atom, studied in the early 20th century, the atomic number increases by 1, Z → Z + 1 but the atomic weight stays (almost) the same A → A (mp ≈ mn). One energetic electron e− is emitted from the nucleus. The energy spectrum of the electron is distributed from zero up to Emax and looks like this: (Credit: Wikimedia Commons) Physicists interpreted beta decay as neutron decay n → p + e−, but in that case the electron energy should be sharply peaked near Emax due to energy conservation: En = Ep + Ee− . In 1930 Wolfgang Pauli, a German physicist, postulated the existence of a third particle in beta decay: the neutrino ν, n → p + e− + ν. He doubted it would ever be directly observed. HC 209H: Second Lecture – p.7/10 Atomic Scales: Distance, Mass, Energy −11 Distance. A person is a couple of m tall. The Bohr radius r1 = 5 × 10 m. −27 Mass. A person mass is a few tens of kg. The proton mass is mp = 2 × 10 kg. −18 Energy. A 60 Watt lightbulb emits 60 J/s. The Bohr energy is E1 = −2 × 10 J. Powers of Ten (graphic is clickable) HC 209H: Second Lecture – p.8/10 Fundamental Particles ca 1935 The following table supersedes the Periodic Table of the elements - all With quantum mechanics, a mathematical ordinary matter is made of these. theory, the detailed chemical properties of elements could be explained based on how Light Heavy Interaction electrons arranged themselves around e− p γ nuclei. However, problems remained... ν n The electrostatic force of repulsion should keep protons in the nucleus apart. What Picture of complex atoms: (stronger) force keeps them bound in the nucleus? What interaction accounts for nuclear beta decay, n → pe−ν? Is the neutrino a real particle or does it just save energy conservation? The proton p and neutron n are very heavy compared to the electron. Are they fundamental particles (in the sense of Democritus) or composite? (Credit: Encyclopedia Brittanica) HC 209H: Second Lecture – p.9/10 Worksheet 2 Preparation A very common unit of energy in particle physics is the electron volt (eV=1.6 × 10−19 J). The eV is the energy gained by an electron passing through a voltage difference of one volt. 103 eV=keV (kilo electron volt) 106 eV=MeV (mega electron volt) 109 eV=GeV (giga electron volt) From E = mc2, a very common unit of mass is the eV/c2, MeV/c2, GeV/c2 etc. 3 Kinetic energy of ideal gas molecule: Ek = 2 kT Depicted here is an electron transitioning from n = 3 to n = 2 2 2 The radii at these n are r3 = 3 r1 = 9r1 and r2 = 2 r1 = 4r1, and the change in energy is 2 2 ∆E = E1/3 − E1/2 = E1(1/9 − 1/4). The energy ∆E lost by the electron appears as a photon γ with wavelength λ = hc/∆E. HC 209H: Second Lecture – p.10/10.
Load more

Recommended publications
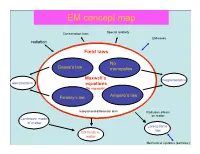
  • EM Concept Map
    EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002.
    [Show full text]
  • Gauss' Linking Number Revisited
    October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery.
    [Show full text]
  • Optical Properties of Bulk and Nano
    Lecture 3: Optical Properties of Bulk and Nano 5 nm Course Info First H/W#1 is due Sept. 10 The Previous Lecture Origin frequency dependence of χ in real materials • Lorentz model (harmonic oscillator model) e- n(ω) n' n'' n'1= ω0 + Nucleus ω0 ω Today optical properties of materials • Insulators (Lattice absorption, color centers…) • Semiconductors (Energy bands, Urbach tail, excitons …) • Metals (Response due to bound and free electrons, plasma oscillations.. ) Optical properties of molecules, nanoparticles, and microparticles Classification Matter: Insulators, Semiconductors, Metals Bonds and bands • One atom, e.g. H. Schrödinger equation: E H+ • Two atoms: bond formation ? H+ +H Every electron contributes one state • Equilibrium distance d (after reaction) Classification Matter ~ 1 eV • Pauli principle: Only 2 electrons in the same electronic state (one spin & one spin ) Classification Matter Atoms with many electrons Empty outer orbitals Outermost electrons interact Form bands Partly filled valence orbitals Filled Energy Inner Electrons in inner shells do not interact shells Do not form bands Distance between atoms Classification Matter Insulators, semiconductors, and metals • Classification based on bandstructure Dispersion and Absorption in Insulators Electronic transitions No transitions Atomic vibrations Refractive Index Various Materials 3.4 3.0 2.0 Refractive index: n’ index: Refractive 1.0 0.1 1.0 10 λ (µm) Color Centers • Insulators with a large EGAP should not show absorption…..or ? • Ion beam irradiation or x-ray exposure result in beautiful colors! • Due to formation of color (absorption) centers….(Homework assignment) Absorption Processes in Semiconductors Absorption spectrum of a typical semiconductor E EC Phonon Photon EV ωPhonon Excitons: Electron and Hole Bound by Coulomb Analogy with H-atom • Electron orbit around a hole is similar to the electron orbit around a H-core • 1913 Niels Bohr: Electron restricted to well-defined orbits n = 1 + -13.6 eV n = 2 n = 3 -3.4 eV -1.51 eV me4 13.6 • Binding energy electron: =−=−=e EB 2 2 eV, n 1,2,3,..
    [Show full text]
  • Bohr Model of Hydrogen
    Chapter 3 Bohr model of hydrogen Figure 3.1: Democritus The atomic theory of matter has a long history, in some ways all the way back to the ancient Greeks (Democritus - ca. 400 BCE - suggested that all things are composed of indivisible \atoms"). From what we can observe, atoms have certain properties and behaviors, which can be summarized as follows: Atoms are small, with diameters on the order of 0:1 nm. Atoms are stable, they do not spontaneously break apart into smaller pieces or collapse. Atoms contain negatively charged electrons, but are electrically neutral. Atoms emit and absorb electromagnetic radiation. Any successful model of atoms must be capable of describing these observed properties. 1 (a) Isaac Newton (b) Joseph von Fraunhofer (c) Gustav Robert Kirch- hoff 3.1 Atomic spectra Even though the spectral nature of light is present in a rainbow, it was not until 1666 that Isaac Newton showed that white light from the sun is com- posed of a continuum of colors (frequencies). Newton introduced the term \spectrum" to describe this phenomenon. His method to measure the spec- trum of light consisted of a small aperture to define a point source of light, a lens to collimate this into a beam of light, a glass spectrum to disperse the colors and a screen on which to observe the resulting spectrum. This is indeed quite close to a modern spectrometer! Newton's analysis was the beginning of the science of spectroscopy (the study of the frequency distri- bution of light from different sources). The first observation of the discrete nature of emission and absorption from atomic systems was made by Joseph Fraunhofer in 1814.
    [Show full text]
  • Particle Nature of Matter
    Solved Problems on the Particle Nature of Matter Charles Asman, Adam Monahan and Malcolm McMillan Department of Physics and Astronomy University of British Columbia, Vancouver, British Columbia, Canada Fall 1999; revised 2011 by Malcolm McMillan Given here are solutions to 5 problems on the particle nature of matter. The solutions were used as a learning-tool for students in the introductory undergraduate course Physics 200 Relativity and Quanta given by Malcolm McMillan at UBC during the 1998 and 1999 Winter Sessions. The solutions were prepared in collaboration with Charles Asman and Adam Monaham who were graduate students in the Department of Physics at the time. The problems are from Chapter 3 The Particle Nature of Matter of the course text Modern Physics by Raymond A. Serway, Clement J. Moses and Curt A. Moyer, Saunders College Publishing, 2nd ed., (1997). Coulomb's Constant and the Elementary Charge When solving numerical problems on the particle nature of matter it is useful to note that the product of Coulomb's constant k = 8:9876 × 109 m2= C2 (1) and the square of the elementary charge e = 1:6022 × 10−19 C (2) is ke2 = 1:4400 eV nm = 1:4400 keV pm = 1:4400 MeV fm (3) where eV = 1:6022 × 10−19 J (4) Breakdown of the Rutherford Scattering Formula: Radius of a Nucleus Problem 3.9, page 39 It is observed that α particles with kinetic energies of 13.9 MeV or higher, incident on copper foils, do not obey Rutherford's (sin φ/2)−4 scattering formula. • Use this observation to estimate the radius of the nucleus of a copper atom.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Series 1 Atoms and Bohr Model.Pdf
    Atoms and the Bohr Model Reading: Gray: (1-1) to (1-7) OGN: (15.1) and (15.4) Outline of First Lecture I. General information about the atom II. How the theory of the atomic structure evolved A. Charge and Mass of the atomic particles 1. Faraday 2. Thomson 3. Millikan B. Rutherford’s Model of the atom Reading: Gray: (1-1) to (1-7) OGN: (15.1) and (15.4) H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn Fr Ra Ac Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lr Atoms consist of: Mass (a.m.u.) Charge (eu) 6 6 Protons ~1 +1 Neutrons ~1 0 C Electrons 1/1836 -1 12.01 10-5 Å (Nucleus) Electron Cloud 1 Å 1 Å = 10 –10 m Note: Nucleus not drawn to scale! HOWHOW DODO WEWE KNOW:KNOW: Atomic Size? Charge and Mass of an Electron? Charge and Mass of a Proton? Mass Distribution in an Atom? Reading: Gray: (1-1) to (1-7) OGN: (15.1) and (15.4) A Timeline of the Atom 400 BC .....
    [Show full text]
  • Arxiv:1512.01765V2 [Physics.Atom-Ph]
    August12,2016 1:27 WSPCProceedings-9.75inx6.5in Antognini˙ICOLS˙3 page 1 1 Muonic atoms and the nuclear structure A. Antognini∗ for the CREMA collaboration Institute for Particle Physics, ETH, 8093 Zurich, Switzerland Laboratory for Particle Physics, Paul Scherrer Institute, 5232 Villigen-PSI, Switzerland ∗E-mail: [email protected] High-precision laser spectroscopy of atomic energy levels enables the measurement of nu- clear properties. Sensitivity to these properties is particularly enhanced in muonic atoms which are bound systems of a muon and a nucleus. Exemplary is the measurement of the proton charge radius from muonic hydrogen performed by the CREMA collaboration which resulted in an order of magnitude more precise charge radius as extracted from other methods but at a variance of 7 standard deviations. Here, we summarize the role of muonic atoms for the extraction of nuclear charge radii, we present the status of the so called “proton charge radius puzzle”, and we sketch how muonic atoms can be used to infer also the magnetic nuclear radii, demonstrating again an interesting interplay between atomic and particle/nuclear physics. Keywords: Proton radius; Muon; Laser spectroscopy, Muonic atoms; Charge and mag- netic radii; Hydrogen; Electron-proton scattering; Hyperfine splitting; Nuclear models. 1. What atomic physics can do for nuclear physics The theory of the energy levels for few electrons systems, which is based on bound- state QED, has an exceptional predictive power that can be systematically improved due to the perturbative nature of the theory itself [1, 2]. On the other side, laser spectroscopy yields spacing between energy levels in these atomic systems so pre- cisely, that even tiny effects related with the nuclear structure already influence several significant digits of these measurements.
    [Show full text]
  • Compton Wavelength, Bohr Radius, Balmer's Formula and G-Factors
    Compton wavelength, Bohr radius, Balmer's formula and g-factors Raji Heyrovska J. Heyrovský Institute of Physical Chemistry, Academy of Sciences of the Czech Republic, Dolejškova 3, 182 23 Prague 8, Czech Republic. [email protected] Abstract. The Balmer formula for the spectrum of atomic hydrogen is shown to be analogous to that in Compton effect and is written in terms of the difference between the absorbed and emitted wavelengths. The g-factors come into play when the atom is subjected to disturbances (like changes in the magnetic and electric fields), and the electron and proton get displaced from their fixed positions giving rise to Zeeman effect, Stark effect, etc. The Bohr radius (aB) of the ground state of a hydrogen atom, the ionization energy (EH) and the Compton wavelengths, λC,e (= h/mec = 2πre) and λC,p (= h/mpc = 2πrp) of the electron and proton respectively, (see [1] for an introduction and literature), are related by the following equations, 2 EH = (1/2)(hc/λH) = (1/2)(e /κ)/aB (1) 2 2 (λC,e + λC,p) = α2πaB = α λH = α /2RH (2) (λC,e + λC,p) = (λout - λin)C,e + (λout - λin)C,p (3) α = vω/c = (re + rp)/aB = 2πaB/λH (4) aB = (αλH/2π) = c(re + rp)/vω = c(τe + τp) = cτB (5) where λH is the wavelength of the ionizing radiation, κ = 4πεo, εo is 2 the electrical permittivity of vacuum, h (= 2πħ = e /2εoαc) is the 2 Planck constant, ħ (= e /κvω) is the angular momentum of spin, α (= vω/c) is the fine structure constant, vω is the velocity of spin [2], re ( = ħ/mec) and rp ( = ħ/mpc) are the radii of the electron and
    [Show full text]
  • Muonic Hydrogen: All Orders Calculations
    Muonic Hydrogen: all orders calculations Paul Indelicato ECT* Workshop on the Proton Radius Puzzle, Trento, October 29-November 2, 2012 Theory • Peter Mohr, National Institute of Standards and Technology, Gaithersburg, Maryland • Paul Indelicato, Laboratoire Kastler Brossel, École Normale Supérieure, CNRS, Université Pierre et Marie Curie, Paris, France and Helmholtz Alliance HA216/ EMMI (Extreme Mater Institute) Trento, October 2012 2 Present status • Published result: – 49 881.88(76)GHz ➙rp= 0.84184(67) fm – CODATA 2006: 0.8768(69) fm (mostly from hydrogen and electron-proton scattering) – Difference: 5 σ • CODATA 2010 (on line since mid-june 2011) – 0.8775 (51) fm – Difference: 6.9 σ – Reasons (P.J. Mohr): • improved hydrogen calculation • new measurement of 1s-3s at LKB (F. Biraben group) • Mainz electron-proton scattering result • The mystery deepens... – Difference on the muonic hydrogen Lamb shift from the two radii: 0.3212 (51 µH) (465 CODATA) meV Trento, October 2012 3 Hydrogen QED corrections QED at order α and α2 Self Energy Vacuum Polarization H-like “One Photon” order α H-like “Two Photon” order α2 = + + +! Z α expansion; replace exact Coulomb propagator by expansion in number of interactions with the nucleus Trento, October 2012 5 Convergence of the Zα expansion Trento, October 2012 6 Two-loop self-energy (1s) V. A. Yerokhin, P. Indelicato, and V. M. Shabaev, Phys. rev. A 71, 040101(R) (2005). Trento, October 2012 7 Two-loop self-energy (1s) V. A. Yerokhin, P. Indelicato, and V. M. Shabaev, Phys. rev. A 71, 040101(R) (2005). V. A. Yerokhin, Physical Review A 80, 040501 (2009) Trento, October 2012 8 Evolution at low-Z All order numerical calculations V.
    [Show full text]
  • Excitons in 3D and 2D Systems
    Excitons in 3D and 2D systems Electrons and holes in an excited semiconductor create a quasiparticle, named exciton. After separation of centre of gravity and relative orbital motion a series of bound exciton states (n=1,2,3…) are located below the band gap. Solving the Schrödinger equation the binding energy in 3D is R * E X (3D) ,n 1,2,.... n n2 *e4 Where R* is the Rydberg energy by R* 2 2 2 2 with µ* as reduced effective mass. It 32 0 defines a series of exciton states which can be populated. In analogy to the hydrogen problem the respective orbital wave function for n=1 is X 1 r (r) exp( ) n1 3/ 2 a0 a0 2 X 4 0 With exciton Bohr radius a (3D) and r=re-rh is the 3D relative electron-hole 0 *e2 coordinate. In k-Space the wave function represented by 3/ 2 X 8 a0 n1 (k) 2 2 2 (1 a0 k ) The k-space representation is important to estimate the oscillator strength of excitonic processes. For discussion of PL excitation spectra and the bleaching of exciton absorption it is important to consider the influence of unbound electron-hole states above the ionization limit (E>0). It is expressed by the Sommerfeld factor 2 R * /( E ) 3D 3D g CEF | E0 (r 0) 1 exp(2 R * /( Eg ) This equation describes the enhancement of absorption above the band gap due to correlated electron-hole pairs. Since equ. Above diverges for Eg one observes a “tooth-like” absorption line.
    [Show full text]
  • The Quantum Condition and an Elastic Limit
    Send Orders for Reprints to [email protected] Open Chemistry Journal, 2014, 1, 21-26 21 Open Access The Quantum Condition and an Elastic Limit Frank Znidarsic P.E. Registered Professional Engineer, State of Pennsylvania Abstract: Charles-Augustin de Coulomb introduced his equations over two centuries ago. These equations quantified the force and the energy of interacting electrical charges. The electrical permittivity of free space was factored into Cou- lomb’s equations. A century later James Clear Maxwell showed that the velocity of light emerged as a consequence this permittivity. These constructs were a crowning achievement of classical physics. In spite of these accomplishments, the philosophy of classical Newtonian physics offered no causative explanation for the quantum condition. Planck’s empirical constant was interjected, ad-hoc, into a description of atomic scale phenomena. Coulomb’s equation was re-factored into the terms of an elastic constant and a wave number. Like Coulomb’s formulation, the new formulation quantified the force and the energy produced by the interaction of electrical charges. The Compton frequency of the electron, the energy levels of the atoms, the energy of the photon, the speed of the atomic electrons, and Planck’s constant, spontaneously emerged from the reformulation. The emergence of these quantities, from a classical analysis, extended the realm of clas- sical physics into a domain that was considered to be exclusively that of the quantum. Keywords: Atomic radii, photoelectric effect, Planck’s constant, the quantum condition. 1. INTRODUCTION with displacement. The Compton frequency, of the electron, emerges as this elasticity acts upon the mass of the electron.
    [Show full text]