DOCSLIB.ORG

Monitoring Progress 1. Slope = 7 Y-Intercept = 2 2. Slope = 1/3 Y

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Monitoring Progress 1. Slope = 7 Y-Intercept = 2 2. Slope = 1/3 Y 4.1 Writing Equations in Slope-intercept Form Notes Vocabulary Definition Picture Linear model Example 1: Write an equation with the given slope Monitoring Progress and y-intercept. 1. Slope = 7 y-intercept = 2 a. slope = -3 y –intercept ½ b. slope = 0 y-intercept -2 2. slope = 1/3 y-intercept = -1 Example 2: Write an equation of each in slope- Monitoring Progress intercept form 3. 4. a. b. Example 3: Write an equation of each line that Monitoring Progress passes through the given points 5. (0, -2) (4, 10) 6. (4, -1) (0, 2) a. (-3, 5) (0, -1) b. (0, -5) (8, -5) Example 4: Write an function f with the values Monitoring Progress f(0) = 10 and f(6) = 34 7. g(0) = 9 and g(8) = 7 Example 5: Monitoring Progress 8. 4.2 Writing Equations in Point-Slope Form Notes Example 1: Write an equation in point-slope Monitoring Progress form of the line that passes through the point 1. (3, -1); m = -2 (-8, 3) and has a slope of ¼ 2. (4, 0); m = -2/3 Example 2: Write an equation in slope-intercept Monitoring Progress form of the line shown. 3. (1, 4) (3, 10) 4. (-4, -1) (8,-4) Example 3: Write a linear function f with the Monitoring Progress values f(4) = -2 and f(8) = 4 5. g(2) = 3 and g(6) = 5 Example 4: Monitoring Progress 6. 4.3 Writing Equations of Parallel and Perpendicular Lines Notes Vocabulary Definition Picture Parallel lines Perpendicular lines Example 1: Determine which of the lines are Monitoring Progress parallel. 1. Line a passes through (-5, 3) & (-6, -1) Line b passes through (3, -2) & (2, -7) are the lines parallel? Example 2: Write an equation of the line that Monitoring Progress passes through (5, -4) and is parallel to the line 2. a. Passes through (-4, 2) Parallel to y = 1/4x + 1 y = 2x + 3 b. Passes through (3, 1) Parallel to y = 3x + 1 Example 3: Determine which of the lines if Monitoring Progress any are parallel or perpendicular. 3. Line a: 2x + 6y = -3 Line b: y = 3x - 8 Line a: y = 4x + 2 Line b: x + 4y = 3 Line c: -8y -2x = 16 Line c: -6y + 18x = 9 Example 4: Write an equation of the line that Monitoring Progress passes through (-3, 1) and is perpendicular to the line y 4. a. passes through (-3, 5) perpendicular to y = -3x -1 = 1/2x + 3 b. passes through (4, -3) perpendicular to y = 4x - 1 Example 5: Monitoring Progress 5. In example 5 a boat is traveling parallel to the shore line and passes through (9, 3). Write an equation that represents the path of the boat. 4.4 Scatter Plots and Lines of Fit Notes Vocabulary Definition Picture Scatter plot Correlation Line of fit Positive Correlation Negative Correlation No Correlation Example 1: The scatter plot shows the amounts x Monitoring Progress (in grams) of sugar and the numbers y of calories in 10 smoothies. 1. How many calories are in the smoothie a. How many calories are in the smoothie that contains that contains 51 grams of sugar? 56 grams of sugar? b. How many grams of sugar are in the smoothie that contains 320 calories? c. What ends to happen to the number of calories as the 2. How many grams of sugar are in the number of grams of sugar increases? smoothie that contains 250 calories? Example 2: Tell whether the data show a Monitoring Progress positive, a negative or no correlation. 3. Make a scatter plot of the data. Tell where the data show a positive, a negative, or no correlation. Example 3: The table shows the weekly sales of a Monitoring Progress DVD and the number of weeks since its release. Write 5. The following data pairs show the monthly income x (in dollars) an equation that models the DVD sales as a function of and the monthly car payment y (in dollars) of six people: (2100, 410) the number of weeks since its release. Interpret the (1650, 315) (1950, 405) (1500, 295) (2250, 440) (1800, 375) slope and y-intercept of the line of fit. 4.5 Analyzing Lines of Fit Notes Vocabulary Definition Picture Residual Linear regression Line of best fit Correlation coefficient interpolation extrapolation causation Example 1: in Example 3 in section 4.4 the equation Example 2: The table shows the age x and salaries y y = -2x + 20 models the data in the table shown. Is the (in thousands of dollars) of eight employees at a model a good fit? company. The equation y = 0.2x + 38 models the data. Is the model a good fit? Week Sales Y-Value residual x y from Age Salaries y Y- residual Model x Value 1 19 from 2 15 Model 35 42 3 13 37 44 4 11 41 47 5 10 43 50 6 8 45 52 7 7 47 51 8 5 53 49 55 45 Monitoring Progress 1: The table shows the attendance y (in thousands) at an amusement park from 2005 to 2014, when x = 0 represents the year 2005. The equation y = -9.8x + 850 models the data. Is the model a good fit? Year Attendance, Y- residual x y Value from Model 0 850 1 845 2 828 3 798 4 800 5 792 6 785 7 781 8 775 9 760 Example 5: Tell whether a correlation is likely in the situation. If so, tell whether there is a causal relationship. Explain your reasoning. a. time spent exercising and the number of calories Example 4: Use the graph or the equation to: burned. y = 12.0x + 35 b. the number of banks and the population of a city. Monitoring Progress 4: Tell whether a a. approximate the duration before a time of 77 minutes correlation is likely in the situation. If so, tell whether there is a causal relationship. Explain your reasoning. b. predict the time after an eruption lasting 7 minutes a. Playing Video games and grade point average. 4.6 Arithmetic Sequences Notes Vocabulary Definition Picture Sequence Term Arithmetic sequence Common difference Example 1: Write the next three terms of the Monitoring Progress: Write the next three arithmetic sequence. terms of the arithmetic sequence. -7, -14, -21, -28 1. -12, 0, 12, 24, … 2. 0.2, 0.6, 1, 1.4, … 3. 4, 3¾, 3½, 3¼, … Example 2: Graph the arithmetic sequence Monitoring Progress: Graph the arithmetic sequence, what do you notice? 4, 8, 12, 16, … What do you notice? 4. 3, 6, 9, 12, … 5. 4, 2, 0, -2, … 6. 1, 0.8, 0.6, 0.4, … Example 3: Does the graph represent an arithmetic Monitoring Progress 7: Does the graph sequence? Explain? represent an arithmetic sequence? Explain? Example 4: Write an equation for the nth term of Monitoring Progress: Write an equation for the arithmetic sequence 14, 11, 8, 5, … Then find a50. the nth term of the arithmetic sequence. Then find a25. 8. 4, 5, 6, 7, … 9. 8, 16, 24, 32, … 10. 1, 0, -1, -2, … Example 5: Online bidding for a purse increases by Monitoring Progress 11: A carnival charges $5 for each bid after the $60 initial bid. $2 for each game after you pay a $5 entry fee. a. Write a function that represents the arithmetic sequence. b. Graph the function. a. Write a function that represents the arithmetic sequence. b. Graph the function. c. the winning bid is $105 how many bids were there? c. How many games can you play when you take $29 to the carnival? 4.7 Piecewise Functions Notes Vocabulary Definition Picture Piecewise functions Step function Absolute value function Example 1 Evaluate the function f Monitoring Progress: above when a. x = 0 b. x = 4 1. f(-8) 2. f(-2) 3. f(0) Example 2 Graphing a Piecewise 4. f(3) 5. f(5) 6. f(10) Monitoring Progress: Graph the function and Domain: Range: describe the domain & Range Monitoring Progress: Graph the function and describe the domain & Range Example 3 Write a piecewise function for the graph. Monitoring progress: Write a piecewise function for the graph. Example 4: You rent a karaoke machine for 5 days. Monitoring Progress 10: A landscaper rents The rental company charges $50 for the first day and a wood chipper for 4 days. The rental company $25 for each additional day. Write and graph a step charges $100 for the first day and $50 for each function that represents the relationship between the additional day. Write and graph a step function that number x of days and the total cost y (in dollars) of represent the relationship between the number of x days and the total cost y (in dollars) of renting the renting the karaoke machine. chipper. Step 1: use table to organize Info Step 2 Write the step function Step 3: Graph the step function .
Load more

Recommended publications
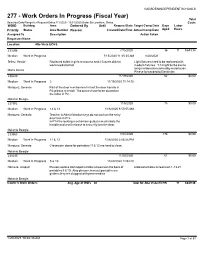
  • Work Orders in Progress
    GADSDEN INDEPENDENT SCHOOLS 277 - Work Orders In Progress (Fiscal Year) Total Selected Date Range for Request Dates:7/1/2020 - 12/31/2020 Order By Location, Status Costs WOID Building Area Deferred By Until Request Date Target Comp Date Days Labor Priority Status Area Number Reason Created Date/Time Actual Comp Date Aged Hours Assigned To Description Action Taken Requester Name Location: Alta Vista ECHS 233356 7/15/2020 36 11 $649.38 Medium Work In Progress 7/15/2020 11:35:35 AM 8/20/2020 Tellez, Hector Replaced bulbs in girls restrooms and 2 fixtures did not Light fixtures need to be replaced with work needs ballast modern fixtures. T-12 light bulbs are no longer ordered or carried by warehouse. Maria Davila Please forwarded to Electrician 238220 11/19/2020 62 $0.00 Medium Work In Progress 2 11/19/2020 11:14:15 Marquez, Gerardo Part of the door mechanism fell out the door handle in P2; please reinstall. The pieces have been placed on the table in P2. Melanie Beegle 237972 11/6/2020 75 $0.00 Medium Work In Progress 12 & 14 11/6/2020 8:50:55 AM Marquez, Gerardo Teacher & Administration keys do not work on the entry door lock in P12. In P14 the locking mechanism gets jammed inside the handle and won't release to securely lock the door. Melanie Beegle 233863 7/28/2020 176 $0.00 Medium Work In Progress 11 & 13 7/28/2020 2:05:26 PM Marquez, Gerardo Classroom doors for portables 11 & 13 are hard to close.
    [Show full text]
  • NAEP 2008 Trends in Academic Progress
    Institute of Education Sciences U.S. Department of Education NCES 2009–479 NAEP 2008 Trends in Academic Progress READING 1971–2008 MATHEMATICS 1973–2008 CONTENTS Executive Summary 2 Executive Summary 6 Introduction This report presents the results of the NAEP long- 8 The Long-Term Trend Assessment term trend assessments in reading and mathemat- in Reading ics, which were most recently given in the 2007–08 28 The Long-Term Trend Assessment school year to students at ages 9, 13, and 17. Nationally representative samples of over 26,000 in Mathematics public and private school students were assessed 50 Technical Notes in each subject area. 53 Appendix Tables The long-term trend assessments make it possible to chart educational progress since the early 1970s. Results in reading are available for 12 assessments going back to the rst in 1971. The rst of 11 assess- ments in mathematics was administered in 1973. What is Throughout this report, the most recent results are compared to those from 2004 and from the rst year The Nation’s the assessment was conducted. ™ Report Card ? The original assessment format, content, and proce- dures were revised somewhat in 2004 to update content The Nation’s Report Card™ informs the public about and provide accommodations to students with disabili- the academacademicic achachievementievement ooff elementarelementaryy and ties and English language learners. The knowledge and secondary students in the United StatesStates. Report skills assessed, however, remain essentially the same cards communicate the findings of the National since the rst assessment year. Assessment of Educational Progress (NAEP), a continuing and nationally representative measure Improvements seen in reading and of achievement in various subjects over time.
    [Show full text]
  • Progress 6 Spaces Progress 6 Spaces. Progress 4 Spaces
    ds You did not reduce your cholesterol by There it is — you’re smoking cigarettes 30%, now the doctor is getting stern: again and the pain in your chest she gave you a prescription for 2 indicates you have damaged your ocar medications but you never filled the coronary arteries! her prescription. t 2 2 A 2 Progress 6 spaces. 1. Progress 6 spaces 2. ® ® ZONE Positively Aging /M. O. R. E. ZONE Positively Aging /M. O. R. E. 2006©The University of Texas Health Science Center at San Antonio 2006©The University of Texas Health Science Center at San Antonio ZONE You quit smoking. Your doctor is concerned because C-reactive protein in your blood is too high, indicating that inflammation is happening somewhere in your body. In your case, it’s in the arteries leading to 2 2 your heart! 3. 4. Regress 1 space. Progress 4 spaces. ® ® ZONE Positively Aging /M. O. R. E. ZONE Positively Aging /M. O. R. E. 2006©The University of Texas Health Science Center at San Antonio 2006©The University of Texas Health Science Center at San Antonio You like to eat fries and burgers in If you are male, spite of the high sodium and cholesterol; so again, you abandon Progress 6 spaces. your healthy eating plan. If you are female, 2 2 5. Do Not Progress 6. Progress 3 spaces or Regress. ® ® ZONE Positively Aging /M. O. R. E. ZONE Positively Aging /M. O. R. E. 2006©The University of Texas Health Science Center at San Antonio 2006©The University of Texas Health Science Center at San Antonio Instead of taking the escalator to the Your doctor just told you your blood second floor, you decide to take the sugar is too high (again).
    [Show full text]
  • Progress 6 Spaces. Regress 1 Space. Progress 7 Spaces. ZONE 3 A
    ds Yikes! Your doctor has told you that Because your atherosclerosis your atherosclerosis is worse and she is progressed, you had angioplasty to talking coronary bypass surgery to clear a seriously blocked artery. A ocar prevent another serious heart attack. stent was placed in your artery to her hold it open. t 3 3 A 3 1. 2. Progress 5 spaces Regress 1 space. Positively Aging®/M. O. R. E. Positively Aging®/M. O. R. E. ZONE ZONE 2006©The University of Texas Health Science Center at San Antonio 2006©The University of Texas Health Science Center at San Antonio ZONE You have atherosclerosis in your That last heart attack was tough! You coronary arteries, and wish you had have been in a cardiac rehabilitation followed the doctor’s recommendations. program for 3 months and are Now you’re really scared; you have a improving. You are still at risk for pain in your chest (angina) and need another heart attack or stroke, but bypass surgery. you have improved. 3 3 3. 4. Progress 6 spaces. Regress 1 space. Positively Aging®/M. O. R. E. Positively Aging®/M. O. R. E. ZONE ZONE 2006©The University of Texas Health Science Center at San Antonio 2006©The University of Texas Health Science Center at San Antonio You have to take blood thinning You have chest pain and have to use medicine to prevent more clots like the nitroglycerin patches to widen (dilate) one that caused your last heart attack. the arteries, improving blood flow to Although you have permanent damage your heart.
    [Show full text]
  • National Seed Strategy
    NATIONAL SEED STRATEGY for Rehabilitation and Restoration Making Progress The Plant Conservation Alliance (PCA) is a public-private partnership of organizations that share the same goal: to protect native plants by ensuring that native plant populations and their communities are maintained, enhanced, and restored. The PCA Federal Committee, chaired by the Bureau of Land Management, developed the “National Seed Strategy for Rehabilitation and Restoration 2015-2020” in cooperation with federal and non-federal partners. For more information on the Plant Conservation Alliance and its members and activities, please visit http://www.blm.gov/pca. Copies of this publication may be obtained online at www.blm.gov/seedstrategy. NATIONAL SEED STRATEGY Making Progress 2 Table of Contents National Seed Strategy for Rehabilitation and Restoration: Making Progress ............................................ 5 Status by Goal ............................................................................................................................................... 6 Goal One ............................................................................................................................................... 6 Goal Two ............................................................................................................................................... 8 Goal Three ............................................................................................................................................. 9 Goal Four ............................................................................................................................................
    [Show full text]
  • Score Interpretation Guide 2017–2018
    SCORE INTERPRETATION GUIDE 2017–2018 Table of Contents Purpose of This Guide .................................................................................................................... 1 Purpose of This Assessment .......................................................................................................... 1 The Use of Alternate Assessments ............................................................................................... 1 Uses of GAA Scores .................................................................................................................... 2 Student Portfolios ......................................................................................................................... 2 Participation Guidelines for the GAA ............................................................................................. 3 Students Assessed ....................................................................................................................... 3 Participation Flowchart .................................................................................................................... 4 Scoring the Georgia Alternate Assessment ................................................................................... 5 Portfolio Scoring ........................................................................................................................... 5 Georgia Alternate Assessment Scoring Rubric ............................................................................. 6 Performance
    [Show full text]
  • School Calendar
    >> Amended School Calendar for COVID-19 Response << HAYS CISD 2020 – 2021 AMENDED CALENDAR 3 Student/ Staff Holiday JULY 2020 JANUARY 2021 1 Student/ Staff Holiday 4 Staff Development & Prep S M T W Th F S S M T W Th F S /Student Holiday 1 2 3 4 1 2 18 Student/ Staff Holiday 5 6 7 8 9 10 11 3 4 5 6 7 8 9 27-28 Early Release High School Only/ Finals 12 13 14 15 16 17 18 10 11 12 13 14 15 16 29 Early Release 6th – 12th 19 20 21 22 23 24 25 17 18 19 20 21 22 23 Grades/ Finals 29 Grading Period/UIL 0 D / 0 E / 0 M / 0 H 26 27 28 29 30 31 24 25 26 27 28 2929]] 30 Eligibility Cut-Off Date 31 18 D / 8,370 E / 8,322 M / 8,025 H 27 & 28 Flexible Staff Days/ Staff AUGUST 2020 FEBRUARY 2021 1 Third 9-Week Grading Development Period Begins (Required teacher contract S M T W Th F S S M T W Th F S 15 Staff Development/ days, but can be scheduled 1 [1 2 3 4 5 6 Student Holiday on other dates.) 31 Staff Development/Prep 2 3 4 5 6 7 8 7 8 9 10 11 12 13 15* Weather Make Up Day (Check district notices. 9 10 11 12 13 14 15 14 15* 16 17 18 19 20 May not be necessary.) 16 17 18 19 20 21 22 21 22 23 24 25 26 27 23 24 25 26 27 28 29 28 0 D / 0 E / 0 M / 0 H 30 31 19 D / 8,835 E / 8,854 M / 8,930 H 1 - 4 Staff Development/Prep SEPTEMBER 2020 MARCH 2021 15-19 Student/ Staff Holidays 7 Student/ Staff Holiday 8 First Day of School/ First S M T W Th F S S M T W Th F S 9-Week Grading Period 1 2 3 4 5 1 2 3 4 5 6 6 7 [8 9 10 11 12 7 8 9 10 11 12 13 13 14 15 16 17 18 19 14 15 16 17 18 19 20 20 21 22 23 24 25 26 21 22 23 24 25 26 27 27 28 29 30 28 29 30 31 18 D / 8,370
    [Show full text]
  • Pilgim's Progress by John Bunyan
    Bunyan: Pilgrim’s Progress 1 The Pilgrim's Progress By John Bunyan, John (1628-1688) www.ccel.org Public Domain Bunyan: Pilgrim’s Progress 2 The Pilgrim's Progress From This World to That Which is to Come; Delivered under the Similitude of a Dream by John Bunyan (1628-1688) Auburn: Derby and Miller. Buffalo: Geo. H. Derby and Co. 1853 Bunyan: Pilgrim’s Progress 3 CONTENTS [1]Author's Apology for his Book [2]PART I. [3]The First Stage. --Christian's deplorable condition--Evangelist directs him--Obstinate and Pliable--Slough of Despond--Worldly Wiseman--Mount Sinai--Conversation with Evangelist [4]The Second Stage. --The Gate--conversation with Good-Will--the Interpreter's House--Christian entertained--the sights there shown him [5]The Third Stage. --Loses his burden at the Cross--Simple, Sloth, Presumption, Formalist, Hypocrisy--hill Difficulty--the Arbor--misses his roll--the palace Beautiful--the lions--talk with Discretion, Piety, Prudence, and Charity--wonders shown to Christian--he is armed [6]The Fourth Stage. --Valley of Humiliation--conflict with Apollyon--Valley of the Shadow of Death--Giants Pope and Pagan [7]The Fifth Stage. --Discourse with Faithful--Talkative and Faithful--Talkative's character [8]The Sixth Stage. --Evangelist overtakes Christian and Faithful--Vanity Fair--the Pilgrims brought to trial--Faithful's mareyrdom [9]The Seventh Stage. --Christian and Hopeful--By-ends and his companions--plain of Ease--Lucre-hill--Demas--the River of Life--Vain-Confidence--Giant Despair--the Pilgrims beaten--the Dungeon--the Key of Promise [10]The Eighth Stage. --The Delectable Mountains--entertained by the Shepherds--a by-way to Hell [11]The Ninth Stage.
    [Show full text]
  • Measuring Student Progress a State-By-State Report Card
    October 2018 Measuring student progress A state-by-state report card Peter Goss and Julie Sonnemann Measuring student progress: A state-by-state report card Grattan Institute Support Grattan Institute Report No. 2018-14, October 2018 Founding members Endowment Supporters This report was written by Dr Peter Goss, Grattan Institute School The Myer Foundation Education Program Director, Julie Sonnemann, School Education National Australia Bank Fellow, and Owain Emslie, Associate. Susan McKinnon Foundation We would like to thank the members of Grattan Institute’s School Education Program Reference Group for their helpful comments, as Affiliate Partners well as numerous government and industry participants and officials for Medibank Private their input. Susan McKinnon Foundation The opinions in this report are those of the authors and do not necessarily represent the views of Grattan Institute’s founding Senior Affiliates members, affiliates, individual board members, reference group Google members or reviewers. Any remaining errors or omissions are the Maddocks responsibility of the authors. PwC Grattan Institute is an independent think-tank focused on Australian McKinsey & Company public policy. Our work is independent, practical and rigorous. We aim The Scanlon Foundation to improve policy outcomes by engaging with both decision makers and the community. Wesfarmers For further information on the Institute’s programs, or to join our mailing Affiliates list, please go to: http://www.grattan.edu.au/. Ashurst This report may be cited as: Goss, P.,
    [Show full text]
  • A Revolution in Progress
    ADUs in CA: A Revolution in Progress | October 2020 | Center for Community Innovation Authors: Karen Chapple, Audrey Lieberworth, Dori Ganetsos, Eric Valchuis, Andrew Kwang & Rachel Schten Acknowledgments We are grateful to the California Department of Housing and Community Development for the funding that helped support this research. We also thank Jenny Liang, Lauren Hom, Jen Hu, and Isaac Schmidt for their invaluable research assistance. The Center for Community Innovation (CCI) at UC Berkeley nurtures effective solutions that expand economic opportunity, diversify housing options, and strengthen connection to place. Center for Community Innovation c/o Institute of Governmental Studies 109 Moses Hall, #2370 Berkeley, CA 94720-237 Table of Conents Table of Contents Executive Summary . 5 Introduction . 7 Methods . 9 Trends in ADU Implementation . 12 Barriers to ADU Development . 18 Best Practices . 23 Missing Middle . 27 Conclusion & Recommendations. 30 Endnotes . 31 Appendices . 33 ADUs in California: A Revolution in Progress 3 Executive Summary Executive Summary Executive Summary Introduction But Barriers Remain In order to address the California (CA) housing crisis, state leg- • Finances (27%), lack of awareness (16%), and lack of desire islators are pursuing zoning reform to allow more small-scale (16%) remain significant barriers to ADU development. Juris- housing types, particularly in low density neighborhoods. Ac- dictions also report that the State’s top-down approach to cessory dwelling units (ADUs), commonly known as secondary this series of ADU legislation presents challenges for local units, backyard cottages, and in-law units, are one such housing ADU construction. type. Over the past few years, state legislators reduced parking requirements, lot size minimums and setback requirements, and • Although lower income and lower resource communities in development fees to incentivize construction of ADUs.
    [Show full text]
  • Students Monitor Academic Progress 1 STUDENTS MONITOR
    Students Monitor Academic Progress 1 STUDENTS MONITOR ACADEMIC PROGRESS USING DATA FOLDERS TO SEE IF ACADEMIC GAINS ARE MADE By JEANNE PEACOCK Submitted to The Educational Leadership Faculty Northwest Missouri State University Missouri Department of Educational Leadership College of Education and Human Services Maryville, MO 64468 Submitted in Fulfillment for the Requirements for 61‐683 Research Paper Summer 2013 July 19, 2014 Students Monitor Academic Progress 2 ABSTRACT The purpose of this study was to analyze elementary student’s academic gains when they monitored their own progress in the areas of reading Dolch Sight Words, Spelling and Math. These students don’t typically monitor their academic progress; it is done by the Special Education Teacher. Progress towards academic goals is made; but there is often regression and progress is typically slow. The research includes findings that answer the question, “Are there academic gains when elementary students monitor their progress using student Data Folders?” In order for the students to have complete ownership of their learning they created their own Data Folders. They created the graph paper and put a title at the top for each subject. After each informal assessment, the students graphed their percentage on the appropriate data graph. The study was conducted during the 2013-2014 school year and compared to the 2012-2013 school year when these same students did not monitor their progress. Six students were involved in this study and their names are anonymous. The findings were analyzed through A Statistical Program (ASP) software. Findings indicate that there is a difference between the progress elementary students’ make when they monitor their own academic progress and when they do not monitor their own academic progress.
    [Show full text]
  • Developing Achievement Levels on the 2011 National Assessment of Educational Progress in Grades 8 and 12 Writing Process Report
    National Assessment Governing Board Developing Achievement Levels on the National Assessment of Educational Progress in Writing Grades 8 and 12 in 2011 Submitted to: National Assessment Governing Board 800 North Capitol Street, NW, Suite 825 Washington, DC 02002-4233 Phone: 202.357.6938 This study was funded by the National Assessment Governing Board under Contract ED-NAG-10-C-0003. Submitted by: Measured Progress 100 Education Way Dover, NH 03820 Phone: 603.749.9102 ALS Writing Process Report September 2012 PANELIST NAMES REDACTED BY GOVERNING BOARD Developing Achievement Levels on the 2011 National Assessment of Educational Progress in Grades 8 and 12 Writing Process Report Luz Bay with Chris Clough Jennifer Dunn Wonsuk Kim Leah McGuire Tia Sukin September 2012 ALS Writing Process Report Measured Progress ii National Assessment Governing Board BOARD MEMBERSHIP (2011–2012) Honorable David P. Driscoll, Chair Former Commissioner of Education Melrose, Massachusetts Mary Frances Taymans, SND, Vice Chair Sisters of Notre Dame National Education Office Bethesda, Maryland Andrés Alonso Shannon Garrison Chief Executive Officer Fourth-Grade Teacher Baltimore City Public Schools Solano Avenue Elementary School Baltimore, Maryland Los Angeles, California David J. Alukonis Doris R. Hicks Former Chairman Principal and Chief Executive Officer Hudson School Board Dr. Martin Luther King, Jr. Charter School Hudson, New Hampshire for Science and Technology New Orleans, Louisiana Louis M. Fabrizio Data, Research and Federal Policy Director Honorable Terry Holliday North Carolina Department of Public Commissioner of Education Instruction Kentucky Department of Education Raleigh, North Carolina Lexington, Kentucky Honorable Anitere Flores Richard Brent Houston Senator Principal Florida State Senate Shawnee Middle School Miami, Florida Shawnee, Oklahoma Alan J.
    [Show full text]