Fluid Flow in Porous Media: a Combined Numerical And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tierärzte Mit Zusatzausbildung Für Augenheilkunde
Tierärzte mit Zusatzausbildung für Augenheilkunde Diese Liste ist eine Aufzählung von Tierärzten, die eine Zusatzausbildung in Augenheilkunde gemacht haben. Sie wurde zusammengestellt mit Hilfe der Informationen des DOK und der Landestierärztekammern. Die Liste ist ein Service des Clubs für Britische Hütehunde. Sie erhebt keinen Anspruch auf Vollständigkeit und stellt keine Empfehlung dar. Wir nehmen gerne zusätzliche Adressen auf, wenn uns diese unter Nachweis der Zusatzausbildung beim DOK oder nach den Vorgaben der Weiterbildungsverordnungen der Landestierärztekammern gemeldet werden. Die aktuelle Liste des DOK können Sie unter http://www.dok-vet.de/ finden. CfBrH, Referentin für Zuchtfragen, Vera Bochdalofsky, Hohenfelde 54a, 21720 Mittelnkirchen, Tel.: 04142/81 25 44 Dr. Jörg-Peter Popp (DOK) Diagnostikzentrum für Kleintiere Tierärztliche Klinik Dr. Jörg-Peter Popp Semperstrasse 3c 01069 Dresden [email protected] 03514722898 Dr. Christina Espich Kleintierpraxis Dorfstrasse 36 03096 Briesen [email protected] 035606/4606 Dr. Andrea Steinmetz Universität Leipzig (DOK) An den Tierkliniken 23 04103 Leipzig Tel.: 0341 / 9738700 E-Mail: [email protected] Dr. Susanne Voig Tierärztliche Praxis für Augenheilkunde +t Dres. von Krosigk und Voigt Delitzscher Straße 69 04129 Leipzig [email protected] 034191027515 Dr. Ullrich Seidel Tierarztpraxis Windorfer Str. 24 04229 Leipzig Tel.: 0341 / 4249010 Dr. Katrin Penschuck Lausicker Str. 31 A 04299 Leipzig Tel.: 0341- 8775622 Dr. Bettina Rohrbach Arndtstr. 11 04416 Markkleeberg Tel.: 0341 / 3389013 Dr. Gerhard Woitow (DOK) Theodor-Lieser-Str. 11 + 06120 Halle Tel.: 0345/5522513 E-Mail: [email protected] Stand 05./2020 Dr. Manuela Schwede (DOK) Tierärztliche Klinik für Kleintiere u.Pferde Fröbelstr. 25 06886 Lutherstadt Wittenberg Tel.: 03491/663015 Fax: 03491/663016 E-Mail: [email protected] Dr. -
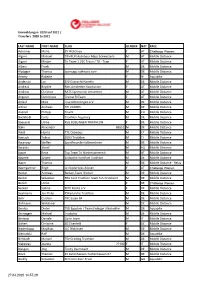
Startliste Challenge-Kaiserwinkl-Walchsee
Ummeldungen 2020 auf 2021 / Transfers 2020 to 2021 LAST NAME FIRST NAME CLUB GENDER NAT RACE Achorner Maria EV Walchsee F AT Challenge Women Aigner Michael TRI+RUN Autohaus Mayr Schwarzach M AT Middle Distance Aigner Miriam Tri Team 1.USC Traun / TD - Train F AT Middle Distance Albers Frank M DE Middle Distance Alpögger Thomas team.ggu-software.com M DE Middle Distance Ancery Babette F NL Aquabike Anderson Ian ESV Eintracht Hameln M DE Middle Distance Andreas Brigitte Rats Amstetten Sportunion F AT Middle Distance Andreas Christian RATS Sportunion Amstetten M AT Middle Distance Angerer Dominique TrumerTriTeam F AT Middle Distance Anlauf Mike Tria Echterdingen e.V. M DE Middle Distance Artner Andreas TRI LIZARDS M DE Middle Distance Avenell Philipp Triamt M CH Middle Distance Bachheibl Carlo Triathlon Augsburg M DE Middle Distance Baeuerle Ulrike RSG BÖBLINGEN TRIATHLON F DE Middle Distance Bahn Alexander 86551 M DE Middle Distance Baláš Honza TTC Olomouc M CZ Middle Distance Banczyk Tobias SG03 Triathlon M CI Middle Distance Baranyay Steffen Sportfreunde Haßmersheim M DE Middle Distance Barasits József M HU Middle Distance Bauer Rene Top Team Tri Niederösterreich M AT Middle Distance Bäuerle Jürgen Eintracht Frankfurt Triathlon M DE Middle Distance Baum Thomas M DE Middle Distance - Relay Baumgartner Birgit Lc-Niederwies-Kössen F AT Challenge Women Becker Andreas Becker-Team Weiher M DE Middle Distance Becker Sebastian REA Card Triathlon Team TuS Griesheim M DE Middle Distance Becker Ulrike F DE Challenge Women Beckert Sabine MTV Förste -

Quintessence Journals
pyri SCIENCECo gh Not for Publicationt b y Q u J. Neugebauera, F. Kistlerb, S. Kistlerc, G. Zündorfd, D. Freyere, L. Ritterf, T. Dreiseidlerg, iJ. Kuschh, N n o t t r f e o J. E. Zölleri ssence CAD/CAM-produced Surgical Guides: Optimizing the Treatment Workflow CAD-CAM-gefertigte Bohrschablonen: Optimierter Behandlungsablauf a Priv.-Doz. Dr. Jörg Neugebauer, Zahnärztliche Gemeinschaft- a PhD, Dr Jörg Neugebauer, Interdisciplinary Outpatient Depart- spraxis, Landsberg am Lech; Interdisziplinäre Poliklinik für Orale ment for Oral Surgery and Implantology, Department of Cra- Chirurgie und Implantologie, Klinik und Poliklinik für Mund-, niomaxillofacial and Plastic Surgery, University of Cologne, Kiefer- und Plastische Gesichtschirurgie der Universität zu Köln Germany b Dr. Frank Kistler, Zahnärztliche Gemeinschaftspraxis, Lands- b Dr Frank Kistler, Private Dental Clinic, Landsberg am Lech, berg am Lech Germany c Dr. med. dent. Steffen Kistler, Zahnärztliche Gemeinschaft- c Dr med dent Steffen Kistler, Private Dental Clinic, Landsberg spraxis, Landsberg am Lech am Lech, Germany d Dr. Gerhard Zündorf, SICAT GmbH & Co. KG, Bonn d Dr Gerhard Zündorf, SICAT Co., Bonn, Germany e Dirk Freyer, SICAT GmbH & Co. KG, Bonn e Dirk Freyer, SICAT Co., Bonn, Germany f Dr. Dr. Lutz Ritter, Interdisziplinäre Poliklinik für Orale Chirur- f Dr Dr Lutz Ritter, Interdisciplinary Outpatient Department for gie und Implantologie, Klinik und Poliklinik für Mund-, Kiefer- Oral Surgery and Implantology, Department of Craniomaxil- und Plastische Gesichtschirurgie der Universität zu Köln lofacial and Plastic Surgery, University of Cologne, Germany g Dr. Dr. Timo Dreiseidler, Interdisziplinäre Poliklinik für Orale g Dr Dr Timo Dreiseidler, Interdisciplinary Outpatient Department Chirurgie und Implantologie, Klinik und Poliklinik für Mund-, for Oral Surgery and Implantology, Department of Craniomaxil- Kiefer- und Plastische Gesichtschirurgie der Universität zu Köln lofacial and Plastic Surgery, University of Cologne, Germany h Jochen Kusch, SICAT GmbH & Co. -

Übersicht Der Betriebsstellen Und Deren Abkürzungen Aus Der Richtlinie 100
Übersicht der Betriebsstellen und deren Abkürzungen aus der Richtlinie 100 XNTH `t Harde HADB Adelebsen KAHM Ahrweiler Markt YMMBM 6,1/60,3 Bad MGH HADH Adelheide MAIC Aich/Nbay KA Aachen Hbf MAD Adelschlag MAI Aichach KASZ Aachen Schanz NADM Adelsdf/Mittelfr TAI Aichstetten KAS Aachen Süd RADN Adelsheim Nord XCAI Aidyrlia KXA Aachen Süd Gr TAD Adelsheim Ost XSAL Aigle KAW Aachen West AADF Adendorf XFAB Aigueblanche KAW G Aachen West Gbf XUAJ Adjud XFAM Aime-la-Plagne KXAW Aachen West Gr XCAD Adler MAIN Ainring KAW P Aachen West Pbf DADO Adorf (Erzg) MAIL Aipl KAW W Aachen West Wk DADG Adorf (V) DB-Gr XIAE Airole KAG Aachen-Gemmenich DAD Adorf (Vogtl) XSAI Airolo XDA Aalborg TAF Affaltrach TAIB Aischbach XDAV Aalborg Vestby XSAA Affoltern Albis MAIT Aitrang TA Aalen XSAW Affoltern-Weier XFAX Aix-en-Prov TGV XBAAL Aalter MAGD Agatharied XFAI Aix-les-Bains XSA Aarau AABG Agathenburg XMAJ Ajka XSABO Aarburg-Oftring XFAG Agde XMAG Ajka-Gyartelep XDAR Aarhus H RAG Aglasterhausen LAK Aken (Elbe) XDARH Aarhus Havn XIACC Agliano-C C XOA Al XMAA Abaliget XIAG Agrigento Centr. XIAL Ala XCAB Abdulino RA Aha XIAO Alassio HABZ Abelitz EAHS Ahaus XIALB Alba KAB Abenden HAHN Ahausen XIALA Alba Adriatica MABG Abensberg WABG Ahlbeck Grenze XUAI Alba Iulia XMAH Abrahamhegy WABO Ahlbeck Ostseeth XIAT Albate Camerlata NAHF Aburg Hochschule HAHM Ahlem RAL Albbruck NAH G Aburg-Goldbach EAHL Ahlen (Westf) XIAB Albenga EDOBZ Abzw Dbw EAHLG Ahlen Gbf AAL Albersdorf HACC Accum EAHLH Ahlen Notbstg EABL Albersloh XFAC Acheres Triage HAHO Ahlhorn RAR Albersweiler(Pf) RAH Achern HAH Ahlshausen XFAL Albertville RAH H Achern Bstg HALT Ahlten FAG Albig RAH F Achern (F) FATC Ahnatal-Casselbr LALB Albrechtshaus RAHG Achern DB/SWEG FHEH Ahnatal-Heckersh FALS Albshausen XFAH Achiet FWEI Ahnatal-Weimar RAM Albsheim(Eis) HACH Achim MAHN Ahrain TAOM Albst.-Onstmett. -

Restructuring the US Military Bases in Germany Scope, Impacts, and Opportunities
B.I.C.C BONN INTERNATIONAL CENTER FOR CONVERSION . INTERNATIONALES KONVERSIONSZENTRUM BONN report4 Restructuring the US Military Bases in Germany Scope, Impacts, and Opportunities june 95 Introduction 4 In 1996 the United States will complete its dramatic post-Cold US Forces in Germany 8 War military restructuring in ● Military Infrastructure in Germany: From Occupation to Cooperation 10 Germany. The results are stag- ● Sharing the Burden of Defense: gering. In a six-year period the A Survey of the US Bases in United States will have closed or Germany During the Cold War 12 reduced almost 90 percent of its ● After the Cold War: bases, withdrawn more than contents Restructuring the US Presence 150,000 US military personnel, in Germany 17 and returned enough combined ● Map: US Base-Closures land to create a new federal state. 1990-1996 19 ● Endstate: The Emerging US The withdrawal will have a serious Base Structure in Germany 23 affect on many of the communi- ties that hosted US bases. The US Impact on the German Economy 26 military’syearly demand for goods and services in Germany has fal- ● The Economic Impact 28 len by more than US $3 billion, ● Impact on the Real Estate and more than 70,000 Germans Market 36 have lost their jobs through direct and indirect effects. Closing, Returning, and Converting US Bases 42 Local officials’ ability to replace those jobs by converting closed ● The Decision Process 44 bases will depend on several key ● Post-Closure US-German factors. The condition, location, Negotiations 45 and type of facility will frequently ● The German Base Disposal dictate the possible conversion Process 47 options. -

Volunteer Translator Pack
TRANSLATION EDITORIAL PRINCIPLES 1. Principles for text, images and audio (a) General principles • Retain the intention, style and distinctive features of the source. • Retain source language names of people, places and organisations; add translations of the latter. • Maintain the characteristics of the source even if these seem difficult or unusual. • Where in doubt make footnotes indicating changes, decisions and queries. • Avoid modern or slang phrases that might be seem anachronistic, with preference for less time-bound figures of speech. • Try to identify and inform The Wiener Library about anything contentious that might be libellous or defamatory. • The Wiener Library is the final arbiter in any disputes of style, translation, usage or presentation. • If the item is a handwritten document, please provide a transcription of the source language as well as a translation into the target language. (a) Text • Use English according to the agreed house style: which is appropriate to its subject matter and as free as possible of redundant or superfluous words, misleading analogies or metaphor and repetitious vocabulary. • Wherever possible use preferred terminology from the Library’s Keyword thesaurus. The Subject and Geographical Keyword thesaurus can be found in this pack. The Institutional thesaurus and Personal Name thesaurus can be provided on request. • Restrict small changes or substitutions to those that help to render the source faithfully in the target language. • Attempt to translate idiomatic expressions so as to retain the colour and intention of the source culture. If this is impossible retain the expression and add translations in a footnote. • Wherever possible do not alter the text structure or sequence. -

Leadingre Member Directory | Residential
Residential Member Directory VON POLL IMMOBILIEN Feldbergstraße 35 +49 69 269 157 410 [email protected] Frankfurt, 60323 www.von-poll.com 350 Offices 1,500 Agents Title Name Email Phone # Broker Daniel Ritter [email protected] +49 69 269 157 410 Relocation Director Sanda Mesinovic [email protected] +49 69 269 157 410 Incoming Coordinator Laura Battiato [email protected] +49 69 269 157 410 Outgoing Coordinator Durmus Avci [email protected] +49 69 269 157 410 Property Management Sanda Mesinovic [email protected] +49 69 269 157 410 Elead Contact Sanda Mesinovic [email protected] +49 69 269 157 410 Corporate Relocation Sanda Mesinovic [email protected] +49 69 269 157 410 Company Designations Applies Service Tiers Applies Certified Commercial Investment Member Certified Real Estate Brokerage Manager Certified Relocation Professional Certified Residential Specialist Worldwide ERC Member Global Mobility Specialist Global Relocation Professional Luxury Portfolio Membership Military On The Move RELO Quality Certified Web Site Quality Certified Agent Certifications Applies Buffini Member Agents LeadingRE Marketing Specialist LeadingRE Service Expert LeadingRE Sales Specialist Ninja Certified Agents Senior Real Estate Specialists Agents Tom Ferry Member Agents City State / Province Country Kitzbuehel AUT Salzburg Salzburg AUT Aachen DEU Ahrensburg DEU Alzey DEU Ansbach DEU Ascheberg DEU Augsburg DEU Bad Homburg DEU Bad Kreuznach DEU Bad Nauheim DEU Bad Schwartau -
Short Programme Llenges
Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Pro- gramme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Pro- gramme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Pro- gramme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short ProgrammeDPG-Frühjahrstagung Short Programme Short Programme Short Programme Short Programme Short Pro- Lasers for Scientifi c Challengesgramme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme Short Programme(Spring Short ProgrammeMeeting) Short Programme Short Programme Short Programme Short Programme -

1. Sz Melléklet Virtuális Telefonszámok / Alközponti Szolgáltatások Díjazása
1. sz melléklet 142 Virtuális telefonszámok / alközponti szolgáltatások díjazása Hatályos: 2020. Szeptember 1.-től (Az árak Bruttó összeget tartalmaznak!) 1. Virtuális telefonszámok díjazása: Ország Város Előhívó Csatornák száma Egyszeri díj* Havidíj Argentina Buenos Aires 54-11 0 2 975,00 Ft 2 975,00 Ft Argentina Buenos Aires 54-11 2 5 100,00 Ft 5 100,00 Ft Argentina Mar Del Plata 54-223 0 2 975,00 Ft 2 975,00 Ft Argentina Mar Del Plata 54-223 2 5 100,00 Ft 5 100,00 Ft Argentina La Plata 54-221 0 2 975,00 Ft 2 975,00 Ft Argentina La Plata 54-221 2 5 100,00 Ft 5 100,00 Ft Argentina Mendoza 54-261 0 2 975,00 Ft 2 975,00 Ft Argentina Mendoza 54-261 2 5 100,00 Ft 5 100,00 Ft Argentina Cordoba 54-351 0 2 975,00 Ft 2 975,00 Ft Argentina Cordoba 54-351 2 5 100,00 Ft 5 100,00 Ft Argentina Rosario 54-341 0 2 975,00 Ft 2 975,00 Ft Argentina Rosario 54-341 2 5 100,00 Ft 5 100,00 Ft Argentina Bahia Blanca 54-291 0 2 975,00 Ft 2 975,00 Ft Argentina Bahia Blanca 54-291 2 5 100,00 Ft 5 100,00 Ft Argentina San Luis 54-2664 0 2 975,00 Ft 2 975,00 Ft Argentina San Luis 54-2664 2 5 100,00 Ft 5 100,00 Ft Argentina Neuquen 54-299 0 2 975,00 Ft 2 975,00 Ft Argentina Neuquen 54-299 2 5 100,00 Ft 5 100,00 Ft Argentina Tucuman 54-381 0 2 975,00 Ft 2 975,00 Ft Argentina Tucuman 54-381 2 5 100,00 Ft 5 100,00 Ft Argentina Glew 54-2224 0 2 975,00 Ft 2 975,00 Ft Argentina Glew 54-2224 2 5 100,00 Ft 5 100,00 Ft Argentina Lujan 54-2323 0 2 975,00 Ft 2 975,00 Ft Argentina Lujan 54-2323 2 5 100,00 Ft 5 100,00 Ft Argentina Parana 54-3434 0 2 975,00 Ft 2 975,00 Ft Argentina -

Hessische Familienkunde
B 20952 Hessische Familienkunde Herausgegeben von der Arbeitsgemeinschaft der familienkundlichen Gesellschaften in Hessen Band 33 2010 Hessische Familienkunde Inhalt und Register der Namen und der Orte von Band 33 (2010) In Arbeitsgemeinschaft herausgegeben von: Gesellschaft für Familienkunde in Kurhessen und Waldeck e.V., Kassel Familienkundliche Gesellschaft für Nassau und Frankfurt e.V., Wiesbaden Hessische Familiengeschichtliche Vereinigung e.V., Darmstadt Schriftleitung: Dr. Lupold v. Lehsten, Nußallee 28, 64625 Bensheim in Verbindung mit den Vorsitzenden der familienkundlichen Gesellschaften in Hessen II HFK 33, Register Mitarbeiter Amelung, Diethard, Prof. Dr., Niebergallweg 1, 64285 Darmstadt Bayer, Johann, Dresdner Str. 9, 35510 Butzbach, [email protected] Bratfisch, Volker, Scheffelstr. 19, 69469 Weinheim, volker.bratfisch—[email protected] Buhr, Jannik, c/o Institut für Personengeschichte, Hauptstraße 65, 64625 Bensheim Franz, Prof. Dr. Eckhart G., Karolinenplatz 3, 64289 Darmstadt Fuchs, Manfred, Im Schützenacker 6, 69181 Leimen Grünwald, Oliver, Schwarzer Weg 11a, 25474 Bönningstedt Kerner, Hubert, Am Pfaffenberg 11, 35789 Weilmünster/Taunus Kirchner, Dipl.-Archivar Christian, Am Pappelhain 2d, 09212 Limbach-Oberfrohna Köhler, Brigitte, Pragelatostr, 20, 64372 Wembach, [email protected] Mittenhuber, Karl-Heinz, Hagenstr. 1, 64407 Fränkisch-Crumbach Oeser, Christoph J., Kirchgasse 5, 64546 Mörfelden Richau, Martin, Dr., Wiesbadener Str. 58f, 14197 Berlin Ronellenfitsch, Klaus, Schwetzinger Str. 67e, 69190 Waldof Schrecker, Til, Agnesstr. 33, 67549 Worms, [email protected] Schüßler, Hans Hartmut, Sudetenstr. 22, 65239 Hochheim am Main, [email protected] Spies, Martin, Wetzlar, [email protected] Steinl, Gerhard, Stettiner Str. 25, 35410 Hungen Vollmar, Werner, Wiesenweg 36, 58119 Hagen Wächter, Marion, Gießen, [email protected] Wiechert, Gabriele, Am Sulzbach 22, 65843 Sulzbach Wiesemann, Volker, Spiekerookstr. -

Listdpcampsbyteamno.Pdf
Land Geallieerde Zone Team nr Location teams Camp Germany American zone, District no. 5 Team 1 Füssen Germany French Zone, Northern district Team 2 Landstuhl Germany American zone, District no. 3 Team 3 Bamberg Giessen (Verdun Kaserne) Germany American zone, District no. 1 Team … Schwäbisch Gmünd Motor pool, Hardt-Kaserne (Polish), Germany British zone, Westfalen region Team 5 Hagen Germany British zone, Westfalen region Team 6 Paderborn Germany British zone, Westfalen region Team 7 Haltern am See Germany British zone, North Rhine region Team 8 Duisdorf Euskirchen Camp Germany American zone, District no. 2 Team 9 Darmstadt Germany American zone, District no. 2 Team 10 Giessen Berg Kaserne Germany British zone, Westfalen region Team 11 Greven Germany British zone, North Rhine region Team 12 Dorsten Doistein Camp Germany British zone, Hannover region Team 13 Hameln Germany French Zone, Northern district Team 14 Wittlich Germany French Zone, Northern district Team 15 Lebach Sammellager für ausländische Arbeiter Kaserne Lebach Germany French Zone, Northern district Team 15 Trier-Kemmel Germany British zone, North Rhine region Team 16 Düsseldorf Germany French Zone, Northern district Team 17 Landstuhl Germany French Zone, Northern district Team 18 Baumholder Germany French Zone, Northern district Team 19 Trier Germany French Zone, Northern district Team 20 Koblenz Germany American zone, District no. 5 Team 21 Augsburg Germany British zone, Westfalen region Team 22 Melle Germany American zone, District no. 1 Team 23 Mannheim Germany British zone, North Rhine region Team 25 Köln Germany French Zone, Northern district Team 26 Homburg Germany American zone, District no. 2 Team 27 Hanau Germany American zone, District no. -

International Registration Designating India Trade Marks Journal No: 1964 , 07/09/2020 Class 1
International Registration designating India Trade Marks Journal No: 1964 , 07/09/2020 Class 1 4551571 02/03/2020 [International Registration No. : 1533612] LIFE TECHNOLOGIES CORPORATION 5791 Van Allen Way Carlsbad CA 92008 United States of America Address for service in India/Attorney address: ZEUSIP ADVOCATES LLP C-4,Jangpura Extension, New Delhi-110014 Proposed to be Used IR DIVISION Reagents for scientific research and diagnostic purposes, namely, clonal isolates adapted to serum-free culture for the transfection, expression and production of recombinant proteins. 9963 Trade Marks Journal No: 1964 , 07/09/2020 Class 1 Priority claimed from 14/01/2020; Application No. : 4614031 ;France 4596149 10/06/2020 [International Registration No. : 1542565] BIO SPRINGER 103, rue Jean Jaurès F-94700 MAISONS ALFORT France Proposed to be Used IR DIVISION Yeast proteins (raw materials), proteins used for beverage production, food protein used as raw material, proteins for the food industry, proteins for fermentation processes. 9964 Trade Marks Journal No: 1964 , 07/09/2020 Class 1 4604587 25/05/2020 [International Registration No. : 1544507] Celotech chemical Co., Ltd Room 101, Complex Building North, Second Floor, No. 48 Zoumatang Road, Mudu, 215000 Wuzhongqu, Suzhou, Jiangsu China Proposed to be Used IR DIVISION Cellulose ethers for industrial purposes; starch for industrial purposes; cellulose; cellulose esters for industrial purposes; cellulose derivatives [chemicals]; glucosides; celluloid. 9965 Trade Marks Journal No: 1964 , 07/09/2020 Class