DOCSLIB.ORG

2.161 Signal Processing: Continuous and Discrete Fall 2008

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2.161 Signal Processing: Continuous and Discrete Fall 2008 MIT OpenCourseWare http://ocw.mit.edu 2.161 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Institute of Technology Department of Mechanical Engineering 2.161 Signal Processing - Continuous and Discrete Fall Term 2008 Lecture 221 Reading: ² Proakis and Manolakis: Secs. 12,1 – 12.2 ² Oppenheim, Schafer, and Buck: ² Stearns and Hush: Ch. 13 1 The Correlation Functions (continued) In Lecture 21 we introduced the auto-correlation and cross-correlation functions as measures of self- and cross-similarity as a function of delay ¿ . We continue the discussion here. 1.1 The Autocorrelation Function There are three basic definitions (a) For an infinite duration waveform: Z T=2 1 Áff (¿) = lim f(t)f(t + ¿) dt T !1 T ¡T=2 which may be considered as a “power” based definition. (b) For an finite duration waveform: If the waveform exists only in the interval t1 · t · t2 Z t2 ½ff (¿ ) = f(t)f(t + ¿ ) dt t1 which may be considered as a “energy” based definition. (c) For a periodic waveform: If f(t) is periodic with period T Z t0+T 1 Áff (¿) = f(t)f(t + ¿) dt T t0 for an arbitrary t0, which again may be considered as a “power” based definition. 1copyright �c D.Rowell 2008 22–1 Example 1 Find the autocorrelation function of the square pulse of amplitude a and duration T as shown below. f ( t ) a t 0 T The wave form has a finite duration, and the autocorrelation function is Z T ½ff (¿) = f(t)f(t + ¿) dt 0 The autocorrelation function is developed graphically below f ( t ) a t 0 T f ( t + t ) a t - t 0 T - t r f f ( t ) a 2 a 2 T r f f ( t ) = ( - t ) -T 0 T t Z T ¡¿ 2 ½ff (¿ ) = a dt 0 = a2(T ¡ j¿j) ¡ T · ¿ · T = 0 otherwise. 22–2 Example 2 Find the autocorrelation function of the sinusoid f(t) = sin(Ωt + Á). Since f(t) is periodic, the autocorrelation function is defined by the average over one period Z t0+T 1 Áff (¿) = f(t)f(t + ¿) dt: T t0 and with t0 = 0 Z 2¼=­ Ω Áff (¿) = sin(Ωt + Á) sin(Ω(t + ¿) + Á) dt 2¼ 0 1 = cos(Ωt) 2 and we see that Áff (¿) is periodic with period 2¼=Ω and is independent of the phase Á. 1.1.1 Properties of the Auto-correlation Function (1) The autocorrelation functions Áff (¿) and ½ff (¿) are even functions, that is Áff (¡¿) = Áff (¿); and ½ff (¡¿ ) = ½ff (¿): (2) A maximum value of ½ff (¿) (or Áff (¿ ) occurs at delay ¿ = 0, j½ff (¿)j · ½ff (0); and jÁff (¿)j · Áff (0) and we note that Z 1 2 ½ff (0) = f (d) dt ¡1 is the “energy” of the waveform. Similarly Z 1 1 2 Áff (0) = lim f (t) dt T !1 T ¡1 is the mean “power” of f(t). (3) ½ff (¿) contains no phase information, and is independent of the time origin. (4) If f(t) is periodic with period T , Áff (¿) is also periodic with period T . (5) If (1) f(t) has zero mean (¹ = 0), and (2) f(t) is non-periodic, lim ½ff (¿) = 0: ¿ !1 22–3 1.1.2 The Fourier Transform of the Auto-Correlation Function Consider the transient case Z 1 ¡j ­¿ Rf f (j Ω) = ½f f (¿ ) e d¿ ¡1 Z 1 �Z 1 ¶ ¡j ­¿ = f(t)f(t + ¿) dt e d¿ ¡1 ¡1 Z 1 Z 1 j ­t ¡j ­º = f(t) e dt: f(º) e dº ¡1 ¡1 = F (¡j Ω)F (j Ω) = jF (j Ω)j2 or F 2 ½ff (¿) Ã! Rff (j Ω) = jF (j Ω)j where Rff (Ω) is known as the energy density spectrum of the transient waveform f(t). Similarly, the Fourier transform of the power-based autocorrelation function, Áff (¿) Z 1 ¡j ­¿ Φf f (j Ω) = F fÁf f (¿)g = Áff (¿) e d¿ ¡1 à ! Z 1 Z T =2 1 ¡j ­¿ = lim f(t)f(t + ¿) dt e d¿ ¡1 T !1 T ¡T =2 is known as the power density spectrum of an infinite duration waveform. From the properties of the Fourier transform, because the auto-correlation function is a real, even function of ¿, the energy/power density spectrum is a real, even function of Ω, and contains no phase information. 1.1.3 Parseval’s Theorem From the inverse Fourier transform Z 1 Z 1 2 1 ½ff (0) = f (t) dt = Rff (j Ω) dΩ 1 2¼ ¡1 or Z 1 Z 1 2 1 2 f (t) dt = jF (j Ω)j dΩ; 1 2¼ ¡1 which equates the total waveform energy in the time and frequency domains, and which is known as Parseval's theorem. Similarly, for infinite duration waveforms Z T=2 Z 1 2 1 lim f (t) dt = Φ(j Ω) dΩ T !1 ¡T=2 2¼ ¡1 equates the signal power in the two domains. 22–4 1.1.4 Note on the relative “widths” of the Autocorrelation and Power/Energy Spectra As in the case of Fourier analysis of waveforms, there is a general reciprocal relationship between the width of a signals spectrum and the width of its autocorrelation function. ² A narrow autocorrelation function generally implies a “broad” spectrum ff f ( t ) F f f ( j W) broad autocorrelation narrow spectrum t W ² and a “broad” autocorrelation function generally implies a narrow-band waveform. ff f ( t ) F f f ( j W) narrow autocorrelation broad spectrum t W In the limit, if Áff (¿) = ±(¿), then Φff (j Ω) = 1, and the spectrum is defined to be “white”. ff f ( t ) F f f ( j W) "w hite" spectrum im pulse autocorrelation 1 t W 1.2 The Cross-correlation Function The cross-correlation function is a measure of self-similarity between two waveforms f(t) and g(t). As in the case of the auto-correlation functions we need two definitions: Z T=2 1 Áfg(¿) = lim f(t)g(t + ¿) d¿ T !1 T ¡T=2 in the case of infinite duration waveforms, and Z 1 ½fg(¿ ) = f(t)g(t + ¿) d¿ ¡1 for finite duration waveforms. 22–5 Example 3 Find the cross-correlation function between the following two functions f ( t ) g ( t ) T T a a t t 0 T 0 1 T 2 In this case g(t) is a delayed version of f(t). The cross-correlation is rf g ( t ) a 2 0 t T2 - T 1 where the peak occurs at ¿ = T2 ¡ T1 (the delay between the two signals). 1.2.1 Properties of the Cross-Correlation Function (1) Áfg(¿) = Ágf (¡¿ ), and the cross-correlation function is not necessarily an even function. (2) If Áfg(¿) = 0 for all ¿, then f(t) and g(t) are said to be uncorrelated. (3) If g(t) = af(t ¡ T ), where a is a constant, that is g(t) is a scaled and delayed version of f(t), then Áff (¿) will have its maximum value at ¿ = T . Cross-correlation is often used in optimal estimation of delay, such as in echolocation (radar, sonar), and in GPS receivers. 22–6 Example 4 In an echolocation system, a transmitted waveform s(t) is reflected off an object at a distance R and is received a time T = 2R=c sec. later. The received signal r(t) = ®s(t¡T )+n(t) is attenuated by a factor ® and is contaminated by additive noise n(t). R transm itted s ( t ) w a v e f o r m reflecting object s t - T r e c e i v e d a ( ) velocity of propagation: c r ( t ) 2 R w a v e f o r m + delay T = c n ( t ) Z 1 Ásr(¿) = s(t)r(t + ¿) dt 1 Z 1 = s(t)(n(t + ¿) + ®s(t ¡ T + ¿)) dt 1 = Ásn(¿) + ®Áss(¿ ¡ T ) and if the transmitted waveform s(t) and the noise n(t) are uncorrelated, that is Ásn(¿ ) ´ 0, then Ásr(¿) = ®Áss(¿ ¡ T ) that is, a scaled and shifted version of the auto-correlation function of the trans­ mitted waveform – which will have its peak value at ¿ = T , which may be used to form an estimator of the range R. 1.2.2 The Cross-Power/Energy Spectrum We define the cross-power/energy density spectra as the Fourier transforms of the cross- correlation functions: Z 1 ¡j ­¿ Rfg(j Ω) = ½fg(¿) e d¿ ¡1 Z 1 ¡j ­¿ Φfg(j Ω) = Áfg(¿) e d¿: ¡1 Then Z 1 ¡j ­¿ Rfg(j Ω) = ½fg(¿) e d¿ ¡1 Z 1 Z 1 ¡j ­¿ = f(t)g(t + ¿) e dt d¿ ¡1 ¡1 Z 1 Z 1 j ­t ¡j ­º = f(t) e dt g(º) e dº ¡1 ¡1 22–7 or Rfg(j Ω) = F (¡j Ω)G(j Ω) Note that although Rff (j Ω) is real and even (because ½ff (¿) is real and even, this is not the case with the cross-power/energy spectra, Φfg(j Ω) and Rfg(j Ω), and they are in general complex. 2 Linear System Input/Output Relationships with Random In­ puts: Consider a linear system H(j Ω) with a random input f(t). The output will also be random y t f ( t ) ( ) H ( j W ) t t f f f ( ) f y y ( ) Then Y (j Ω) = F (j Ω)H(j Ω); Y (j Ω)Y (¡j Ω) = F (j Ω)H(j Ω)F (¡j Ω)H(¡j Ω) or 2 Φyy(j Ω) = Φff (j Ω) jH(j Ω)j : Also F (¡j Ω)Y (j Ω) = F (¡j Ω)F (j Ω)H(j Ω); or Φfy(j Ω) = Φff (j Ω)H(j Ω): Taking the inverse Fourier transforms © ª ¡1 2 Áyy(¿ ) = Áff (¿) ­ F jH(j Ω)j Áfy(¿ ) = Áff (¿) ­ h(¿ ): 3 Discrete-Time Correlation Define the correlation functions in terms of summations, for example for an infinite length sequence Áfg(n) = E ffmgm+ng N 1 X = lim fmgm+n; N !1 2N + 1 m=¡N and for a finite length sequence N X ½fg(n) = fmgm+n: m=¡N 22–8 The following properties are analogous to the properties of the continuous correlation func­ tions: (1) The auto-correlation functions Á(ff(n) and ½ff (n) are real, even functions.
Load more

Recommended publications
  • Von Mises' Frequentist Approach to Probability
    Section on Statistical Education – JSM 2008 Von Mises’ Frequentist Approach to Probability Milo Schield1 and Thomas V. V. Burnham2 1 Augsburg College, Minneapolis, MN 2 Cognitive Systems, San Antonio, TX Abstract Richard Von Mises (1883-1953), the originator of the birthday problem, viewed statistics and probability theory as a science that deals with and is based on real objects rather than as a branch of mathematics that simply postulates relationships from which conclusions are derived. In this context, he formulated a strict Frequentist approach to probability. This approach is limited to observations where there are sufficient reasons to project future stability – to believe that the relative frequency of the observed attributes would tend to a fixed limit if the observations were continued indefinitely by sampling from a collective. This approach is reviewed. Some suggestions are made for statistical education. 1. Richard von Mises Richard von Mises (1883-1953) may not be well-known by statistical educators even though in 1939 he first proposed a problem that is today widely-known as the birthday problem.1 There are several reasons for this lack of recognition. First, he was educated in engineering and worked in that area for his first 30 years. Second, he published primarily in German. Third, his works in statistics focused more on theoretical foundations. Finally, his inductive approach to deriving the basic operations of probability is very different from the postulate-and-derive approach normally taught in introductory statistics. See Frank (1954) and Studies in Mathematics and Mechanics (1954) for a review of von Mises’ works. This paper is based on his two English-language books on probability: Probability, Statistics and Truth (1936) and Mathematical Theory of Probability and Statistics (1964).
    [Show full text]
  • Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium
    Appl. Sci. 2015, 5, 136-144; doi:10.3390/app5020136 OPEN ACCESS applied sciences ISSN 2076-3417 www.mdpi.com/journal/applsci Article Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium Yoshinari Takao 1,†, Tomoko Imasaka 2,†, Yuichiro Kida 1,† and Totaro Imasaka 1,3,* 1 Department of Applied Chemistry, Graduate School of Engineering, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan; E-Mails: [email protected] (Y.T.); [email protected] (Y.K.) 2 Laboratory of Chemistry, Graduate School of Design, Kyushu University, 4-9-1, Shiobaru, Minami-ku, Fukuoka 815-8540, Japan; E-Mail: [email protected] 3 Division of Optoelectronics and Photonics, Center for Future Chemistry, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +81-92-802-2883; Fax: +81-92-802-2888. Academic Editor: Takayoshi Kobayashi Received: 7 April 2015 / Accepted: 3 June 2015 / Published: 9 June 2015 Abstract: A gas was utilized in producing the third harmonic emission as a nonlinear optical medium for autocorrelation and frequency-resolved optical gating measurements to evaluate the pulse width and chirp of a Ti:sapphire laser. Due to a wide frequency domain available for a gas, this approach has potential for use in measuring the pulse width in the optical (ultraviolet/visible) region beyond one octave and thus for measuring an optical pulse width less than 1 fs.
    [Show full text]
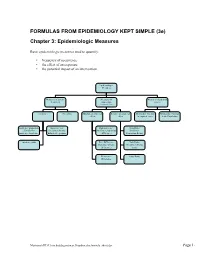
  • FORMULAS from EPIDEMIOLOGY KEPT SIMPLE (3E) Chapter 3: Epidemiologic Measures
    FORMULAS FROM EPIDEMIOLOGY KEPT SIMPLE (3e) Chapter 3: Epidemiologic Measures Basic epidemiologic measures used to quantify: • frequency of occurrence • the effect of an exposure • the potential impact of an intervention. Epidemiologic Measures Measures of disease Measures of Measures of potential frequency association impact (“Measures of Effect”) Incidence Prevalence Absolute measures of Relative measures of Attributable Fraction Attributable Fraction effect effect in exposed cases in the Population Incidence proportion Incidence rate Risk difference Risk Ratio (Cumulative (incidence density, (Incidence proportion (Incidence Incidence, Incidence hazard rate, person- difference) Proportion Ratio) Risk) time rate) Incidence odds Rate Difference Rate Ratio (Incidence density (Incidence density difference) ratio) Prevalence Odds Ratio Difference Macintosh HD:Users:buddygerstman:Dropbox:eks:formula_sheet.doc Page 1 of 7 3.1 Measures of Disease Frequency No. of onsets Incidence Proportion = No. at risk at beginning of follow-up • Also called risk, average risk, and cumulative incidence. • Can be measured in cohorts (closed populations) only. • Requires follow-up of individuals. No. of onsets Incidence Rate = ∑person-time • Also called incidence density and average hazard. • When disease is rare (incidence proportion < 5%), incidence rate ≈ incidence proportion. • In cohorts (closed populations), it is best to sum individual person-time longitudinally. It can also be estimated as Σperson-time ≈ (average population size) × (duration of follow-up). Actuarial adjustments may be needed when the disease outcome is not rare. • In an open populations, Σperson-time ≈ (average population size) × (duration of follow-up). Examples of incidence rates in open populations include: births Crude birth rate (per m) = × m mid-year population size deaths Crude mortality rate (per m) = × m mid-year population size deaths < 1 year of age Infant mortality rate (per m) = × m live births No.
    [Show full text]
  • Power Comparisons of Five Most Commonly Used Autocorrelation Tests
    Pak.j.stat.oper.res. Vol.16 No. 1 2020 pp119-130 DOI: http://dx.doi.org/10.18187/pjsor.v16i1.2691 Pakistan Journal of Statistics and Operation Research Power Comparisons of Five Most Commonly Used Autocorrelation Tests Stanislaus S. Uyanto School of Economics and Business, Atma Jaya Catholic University of Indonesia, [email protected] Abstract In regression analysis, autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated. The consequence is that the estimates of coefficients and their standard errors will be wrong if the autocorrelation is ignored. There are many tests for autocorrelation, we want to know which test is more powerful. We use Monte Carlo methods to compare the power of five most commonly used tests for autocorrelation, namely Durbin-Watson, Breusch-Godfrey, Box–Pierce, Ljung Box, and Runs tests in two different linear regression models. The results indicate the Durbin-Watson test performs better in the regression model without lagged dependent variable, although the advantage over the other tests reduce with increasing autocorrelation and sample sizes. For the model with lagged dependent variable, the Breusch-Godfrey test is generally superior to the other tests. Key Words: Correlated error terms; Ordinary least squares assumption; Residuals; Regression diagnostic; Lagged dependent variable. Mathematical Subject Classification: 62J05; 62J20. 1. Introduction An important assumption of the classical linear regression model states that there is no autocorrelation in the error terms. Autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated, meaning that the Gauss Markov theorem (Plackett, 1949, 1950; Greene, 2018) does not apply, and that ordinary least squares estimators are no longer the best linear unbiased estimators.
    [Show full text]
  • LECTURES 2 - 3 : Stochastic Processes, Autocorrelation Function
    LECTURES 2 - 3 : Stochastic Processes, Autocorrelation function. Stationarity. Important points of Lecture 1: A time series fXtg is a series of observations taken sequentially over time: xt is an observation recorded at a specific time t. Characteristics of times series data: observations are dependent, become available at equally spaced time points and are time-ordered. This is a discrete time series. The purposes of time series analysis are to model and to predict or forecast future values of a series based on the history of that series. 2.2 Some descriptive techniques. (Based on [BD] x1.3 and x1.4) ......................................................................................... Take a step backwards: how do we describe a r.v. or a random vector? ² for a r.v. X: 2 d.f. FX (x) := P (X · x), mean ¹ = EX and variance σ = V ar(X). ² for a r.vector (X1;X2): joint d.f. FX1;X2 (x1; x2) := P (X1 · x1;X2 · x2), marginal d.f.FX1 (x1) := P (X1 · x1) ´ FX1;X2 (x1; 1) 2 2 mean vector (¹1; ¹2) = (EX1; EX2), variances σ1 = V ar(X1); σ2 = V ar(X2), and covariance Cov(X1;X2) = E(X1 ¡ ¹1)(X2 ¡ ¹2) ´ E(X1X2) ¡ ¹1¹2. Often we use correlation = normalized covariance: Cor(X1;X2) = Cov(X1;X2)=fσ1σ2g ......................................................................................... To describe a process X1;X2;::: we define (i) Def. Distribution function: (fi-di) d.f. Ft1:::tn (x1; : : : ; xn) = P (Xt1 · x1;:::;Xtn · xn); i.e. this is the joint d.f. for the vector (Xt1 ;:::;Xtn ). (ii) First- and Second-order moments. ² Mean: ¹X (t) = EXt 2 2 2 2 ² Variance: σX (t) = E(Xt ¡ ¹X (t)) ´ EXt ¡ ¹X (t) 1 ² Autocovariance function: γX (t; s) = Cov(Xt;Xs) = E[(Xt ¡ ¹X (t))(Xs ¡ ¹X (s))] ´ E(XtXs) ¡ ¹X (t)¹X (s) (Note: this is an infinite matrix).
    [Show full text]
  • Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients
    Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients Richard M. Levich and Rosario C. Rizzo * Current Draft: December 1998 Abstract: When autocorrelation is small, existing statistical techniques may not be powerful enough to reject the hypothesis that a series is free of autocorrelation. We propose two new and simple statistical tests (RHO and PHI) based on the unweighted sum of autocorrelation and partial autocorrelation coefficients. We analyze a set of simulated data to show the higher power of RHO and PHI in comparison to conventional tests for autocorrelation, especially in the presence of small but persistent autocorrelation. We show an application of our tests to data on currency futures to demonstrate their practical use. Finally, we indicate how our methodology could be used for a new class of time series models (the Generalized Autoregressive, or GAR models) that take into account the presence of small but persistent autocorrelation. _______________________________________________________________ An earlier version of this paper was presented at the Symposium on Global Integration and Competition, sponsored by the Center for Japan-U.S. Business and Economic Studies, Stern School of Business, New York University, March 27-28, 1997. We thank Paul Samuelson and the other participants at that conference for useful comments. * Stern School of Business, New York University and Research Department, Bank of Italy, respectively. 1 1. Introduction Economic time series are often characterized by positive
    [Show full text]
  • 3 Autocorrelation
    3 Autocorrelation Autocorrelation refers to the correlation of a time series with its own past and future values. Autocorrelation is also sometimes called “lagged correlation” or “serial correlation”, which refers to the correlation between members of a series of numbers arranged in time. Positive autocorrelation might be considered a specific form of “persistence”, a tendency for a system to remain in the same state from one observation to the next. For example, the likelihood of tomorrow being rainy is greater if today is rainy than if today is dry. Geophysical time series are frequently autocorrelated because of inertia or carryover processes in the physical system. For example, the slowly evolving and moving low pressure systems in the atmosphere might impart persistence to daily rainfall. Or the slow drainage of groundwater reserves might impart correlation to successive annual flows of a river. Or stored photosynthates might impart correlation to successive annual values of tree-ring indices. Autocorrelation complicates the application of statistical tests by reducing the effective sample size. Autocorrelation can also complicate the identification of significant covariance or correlation between time series (e.g., precipitation with a tree-ring series). Autocorrelation implies that a time series is predictable, probabilistically, as future values are correlated with current and past values. Three tools for assessing the autocorrelation of a time series are (1) the time series plot, (2) the lagged scatterplot, and (3) the autocorrelation function. 3.1 Time series plot Positively autocorrelated series are sometimes referred to as persistent because positive departures from the mean tend to be followed by positive depatures from the mean, and negative departures from the mean tend to be followed by negative departures (Figure 3.1).
    [Show full text]
  • Fundamental Frequency Detection
    Fundamental Frequency Detection Jan Cernock´y,ˇ Valentina Hubeika cernocky|ihubeika @fit.vutbr.cz { } DCGM FIT BUT Brno Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 1/37 Agenda Fundamental frequency characteristics. • Issues. • Autocorrelation method, AMDF, NFFC. • Formant impact reduction. • Long time predictor. • Cepstrum. • Improvements in fundamental frequency detection. • Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 2/37 Recap – speech production and its model Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 3/37 Introduction Fundamental frequency, pitch, is the frequency vocal cords oscillate on: F . • 0 The period of fundamental frequency, (pitch period) is T = 1 . • 0 F0 The term “lag” denotes the pitch period expressed in samples : L = T Fs, where Fs • 0 is the sampling frequency. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 4/37 Fundamental Frequency Utilization speech synthesis – melody generation. • coding • – in simple encoding such as LPC, reduction of the bit-stream can be reached by separate transfer of the articulatory tract parameters, energy, voiced/unvoiced sound flag and pitch F0. – in more complex encoders (such as RPE-LTP or ACELP in the GSM cell phones) long time predictor LTP is used. LPT is a filter with a “long” impulse response which however contains only few non-zero components. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 5/37 Fundamental Frequency Characteristics F takes the values from 50 Hz (males) to 400 Hz (children), with Fs=8000 Hz these • 0 frequencies correspond to the lags L=160 to 20 samples. It can be seen, that with low values F0 approaches the frame length (20 ms, which corresponds to 160 samples).
    [Show full text]
  • Spatial Autocorrelation: Covariance and Semivariance Semivariance
    Spatial Autocorrelation: Covariance and Semivariancence Lily Housese ­P eters GEOG 593 November 10, 2009 Quantitative Terrain Descriptorsrs Covariance and Semivariogram areare numericc methods used to describe the character of the terrain (ex. Terrain roughness, irregularity) Terrain character has important implications for: 1. the type of sampling strategy chosen 2. estimating DTM accuracy (after sampling and reconstruction) Spatial Autocorrelationon The First Law of Geography ““ Everything is related to everything else, but near things are moo re related than distant things.” (Waldo Tobler) The value of a variable at one point in space is related to the value of that same variable in a nearby location Ex. Moranan ’s I, Gearyary ’s C, LISA Positive Spatial Autocorrelation (Neighbors are similar) Negative Spatial Autocorrelation (Neighbors are dissimilar) R(d) = correlation coefficient of all the points with horizontal interval (d) Covariance The degree of similarity between pairs of surface points The value of similarity is an indicator of the complexity of the terrain surface Smaller the similarity = more complex the terrain surface V = Variance calculated from all N points Cov (d) = Covariance of all points with horizontal interval d Z i = Height of point i M = average height of all points Z i+d = elevation of the point with an interval of d from i Semivariancee Expresses the degree of relationship between points on a surface Equal to half the variance of the differences between all possible points spaced a constant distance apart
    [Show full text]
  • Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique
    Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique Bahar Deler Barry L. Nelson Dept. of IE & MS, Northwestern University September 2000 Abstract We present a model for representing stationary multivariate time series with arbitrary mar- ginal distributions and autocorrelation structures and describe how to generate data quickly and accurately to drive computer simulations. The central idea is to transform a Gaussian vector autoregressive process into the desired multivariate time-series input process that we presume as having a VARTA (Vector-Autoregressive-To-Anything) distribution. We manipulate the correlation structure of the Gaussian vector autoregressive process so that we achieve the desired correlation structure for the simulation input process. For the purpose of computational efficiency, we provide a numerical method, which incorporates a numerical-search procedure and a numerical-integration technique, for solving this correlation-matching problem. Keywords: Computer simulation, vector autoregressive process, vector time series, multivariate input mod- eling, numerical integration. 1 1 Introduction Representing the uncertainty or randomness in a simulated system by an input model is one of the challenging problems in the practical application of computer simulation. There are an abundance of examples, from manufacturing to service applications, where input modeling is critical; e.g., modeling the time to failure for a machining process, the demand per unit time for inventory of a product, or the times between arrivals of calls to a call center. Further, building a large- scale discrete-event stochastic simulation model may require the development of a large number of, possibly multivariate, input models. Development of these models is facilitated by accurate and automated (or nearly automated) input modeling support.
    [Show full text]
  • Pearson-Fisher Chi-Square Statistic Revisited
    Information 2011 , 2, 528-545; doi:10.3390/info2030528 OPEN ACCESS information ISSN 2078-2489 www.mdpi.com/journal/information Communication Pearson-Fisher Chi-Square Statistic Revisited Sorana D. Bolboac ă 1, Lorentz Jäntschi 2,*, Adriana F. Sestra ş 2,3 , Radu E. Sestra ş 2 and Doru C. Pamfil 2 1 “Iuliu Ha ţieganu” University of Medicine and Pharmacy Cluj-Napoca, 6 Louis Pasteur, Cluj-Napoca 400349, Romania; E-Mail: [email protected] 2 University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca, 3-5 M ănăş tur, Cluj-Napoca 400372, Romania; E-Mails: [email protected] (A.F.S.); [email protected] (R.E.S.); [email protected] (D.C.P.) 3 Fruit Research Station, 3-5 Horticultorilor, Cluj-Napoca 400454, Romania * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel: +4-0264-401-775; Fax: +4-0264-401-768. Received: 22 July 2011; in revised form: 20 August 2011 / Accepted: 8 September 2011 / Published: 15 September 2011 Abstract: The Chi-Square test (χ2 test) is a family of tests based on a series of assumptions and is frequently used in the statistical analysis of experimental data. The aim of our paper was to present solutions to common problems when applying the Chi-square tests for testing goodness-of-fit, homogeneity and independence. The main characteristics of these three tests are presented along with various problems related to their application. The main problems identified in the application of the goodness-of-fit test were as follows: defining the frequency classes, calculating the X2 statistic, and applying the χ2 test.
    [Show full text]
  • STAT 830 the Basics of Nonparametric Models The
    STAT 830 The basics of nonparametric models The Empirical Distribution Function { EDF The most common interpretation of probability is that the probability of an event is the long run relative frequency of that event when the basic experiment is repeated over and over independently. So, for instance, if X is a random variable then P (X ≤ x) should be the fraction of X values which turn out to be no more than x in a long sequence of trials. In general an empirical probability or expected value is just such a fraction or average computed from the data. To make this precise, suppose we have a sample X1;:::;Xn of iid real valued random variables. Then we make the following definitions: Definition: The empirical distribution function, or EDF, is n 1 X F^ (x) = 1(X ≤ x): n n i i=1 This is a cumulative distribution function. It is an estimate of F , the cdf of the Xs. People also speak of the empirical distribution of the sample: n 1 X P^(A) = 1(X 2 A) n i i=1 ^ This is the probability distribution whose cdf is Fn. ^ Now we consider the qualities of Fn as an estimate, the standard error of the estimate, the estimated standard error, confidence intervals, simultaneous confidence intervals and so on. To begin with we describe the best known summaries of the quality of an estimator: bias, variance, mean squared error and root mean squared error. Bias, variance, MSE and RMSE There are many ways to judge the quality of estimates of a parameter φ; all of them focus on the distribution of the estimation error φ^−φ.
    [Show full text]