DOCSLIB.ORG

4-5 Subtracting Mixed Numbers 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
4-5 Subtracting Mixed Numbers 1 4-5 4-5 Subtracting Mixed Numbers 1. Plan Lesson Preview What You’ll Learn Check Skills You’ll Need For help, go to Lesson 3-5. OBJECTIVE PowerPoint 1 To subtract mixed numbers Write each improper fraction as a mixed number in simplest form. Check Skills You’ll Need OBJECTIVE 3 8 23 To subtract mixed 11 22 3 2 1.2 2.3 3 3. 45 Writing Fractions as numbers with 2 5 20 15 24 Mixed Numbers renaming 4.21 5.21 6. 22 Lesson 3-5: Example 3. Extra 8 2 6 2 10 5 Practice p. 644. ...And Why 7. Explain the steps you used to write 24 as a mixed number in To subtract two weights, 10 as in Example 1 simplest form. Divide 24 by 10. The quotient 2 is the integer of the Lesson Resources mixed number. The remainder 4 is the numerator, and 10 is the 4 2 denominator: 210 . Reduce to 25 . Teaching Resources OBJECTIVE Practice, Reteaching, Enrichment Interactive lesson includes instant self-check, tutorials, and activities. 1 Subtracting Mixed Numbers Reaching All Students Practice Workbook 4-5 To subtract mixed numbers, first you may need to write the fractions with a Spanish Practice Workbook 4-5 Guided Problem Solving 4-5 common denominator. Then subtract the whole numbers and the fraction Hands-On Activities 14 parts separately. Presentation Assistant Plus! 1 EXAMPLE Real-World Problem Solving Transparencies • Check Skills You’ll Need 4-5 3 Lions At birth, one lion cub weighs 3 pounds. Another cub in the same • Problem of the Day 4-5 5 4 litter weighs 2 pounds. How much more does the heavier cub weigh? • Additional Examples 4-5 8 • Student Edition Answers 4-5 3 5 To calculate the difference in weights, find 3 - 2 . • Lesson Quiz 4-5 4 8 3 6 d 3 6 PH Presentation Pro CD-ROM 4-5 3 3 The LCD is 8. Write as . 4 8 4 8 S 5 5 2 2 2 2 Male cubs grow to an adult 8 8 Computer Test Generator CD Subtract the whole numbers. weight of 600 pounds. 1 d 1 Then subtract the fractions. 8 Technology 1 The heavier cub weighs 1 pounds more than the other cub. Resource Pro® CD-ROM 8 Computer Test Generator CD 3 5 Check for Reasonableness Round each mixed number: 3 < 4; 2 < 3. PH Presentation Pro CD-ROM 4 8 - = 1 Then subtract: 4 3 1. The answer 18 is close to the estimate. So, the www.PHSchool.com answer is reasonable. Student Site 3 7 Teacher Web Code: aak-5500 • Check Understanding 1 a. A supporting wedge for a window is 216 inches wide and 28 inches long. • Self-grading Lesson Quiz 11 How much longer is the wedge than it is wide? 16 in. PH SuccessNet Teacher Center b. Reasoning In Example 1, could you use 32 as the common denominator? • Lesson Planner Explain your answer. Yes; answers may vary. Sample: 32 is a common • Resources multiple of 8 and 4, so it is also a common denominator. Plus 190 Chapter 4 Adding and Subtracting Fractions ANT ST C H N I E C K M S E Y T S Ongoing Assessment and Intervention Before the Lesson During the Lesson After the Lesson Diagnose prerequisite skills using: Monitor progress using: Assess knowledge using: • Check Skills You’ll Need • Check Understanding • Lesson Quiz • Additional Examples • Computer Test Generator CD • Test Prep 190 OBJECTIVE 2 Subtracting Mixed Numbers by Renaming 2. Teach Sometimes you need to rename whole numbers or fractions in order to 1 Math Background subtract from them. Here is how to rename 3 4. Subtracting mixed numbers is Need Help? ϭ 1 1 3 5 2 1 1 similar to adding mixed numbers For help writing mixed 4 4 in that whole numbers and numbers as improper 5 fractions, go to Lesson 3-5. 5 2 1 fraction parts are dealt with 1 5 4 3 ϭ 2 separately and the results are 4 4 5 5 2 combined. The new step in 4 subtracting mixed numbers involves renaming. If the fraction 2 EXAMPLE Renaming Whole Numbers being subtracted is greater than 5 the one from which it is being - 2 Find 7 8. subtracted, the fraction from which you are subtracting must Write 7 as a mixed number. Use 8 for the denominator since you must 5 be renamed. This requires also subtract 8. renaming the whole number part 8 d 8 8 of the mixed number. For 7 6 Rename 7 as 6 1 1 5 6 1 , or 6 . 8 8 8 1 2 S instance, in subtracting 4 5 2 2 5, 1 6 5 5 you rename 4 5 as 3 5. First you 2 2 2 2 8 8 subtract the fractions. Then you 3 d Subtract the whole numbers. subtract the whole numbers. 4 8 Then subtract the fractions. 6 2 4 3 5 2 2 5 5 15 2 1 1 3 Check Understanding 2 Find each difference. a. 5 - 3 1 b. 10 - 4 5 3 3 4 4 Teaching Notes Inclusion 3 EXAMPLE Renaming Mixed Numbers You may need to review how to 2 find the LCD (Least Common Distance (miles) Biology In one hour, a bee can fly 53 miles and a moth can fly Denominator) of two fractions. 1 Moth 11 6 miles. How much farther can the moth fly in one hour? 1 1 EXAMPLE Error Prevention 116 1 2 1 2 1 To answer the question, find 11 - 5 . Since , , rename 11 . 6 3 6 3 6 Guide students to begin with the 2 I fractions’ column when they 5 3 1 2 Estimate 11 2 5 < 11 2 6 5 5 subtract mixed numbers. In Bee Difference 6 3 Example 1 no renaming is 1 7 1 1 7 11 10 d Rename 11 as 10 151 10 . required; but in problems that 6 6 6 6 6 S do require renaming, subtracting d The LCD is 6. Write 2 as 4. the whole numbers first can cause 2 4 3 6 2 5 2 5 3 6 errors. 3 d Subtract. 3. Answers may vary. 5 5 2 EXAMPLE Teaching Tip 6 Sample: If the Call attention to Check benchmark of the 1 d Simplify. first fraction is less 5 5 Understanding 2b. Review that 2 0 than the benchmark 1 10 is the same as 10 4. Ask: Check for Reasonableness The answer 5 is close to the estimate of 5. 4 of the second 2 How do you rename 10? 9 4 fraction, then rename 1 PowerPoint before subtracting. The moth can fly 5 2 miles farther than the bee. Additional Examples Check Understanding 3 Number Sense How can you use benchmarks to tell whether you will have 1 to rename before subtracting? See above left. 1 A black bear is about 5 4 ft long. An Alaskan brown bear 1 is about 7 2 ft long. How much 4-5 Subtracting Mixed Numbers 191 longer is an Alaskan brown 1 bear than a black bear? 2 4 ft 2 1 Reaching All Students 2 Find 9 2 13. 7 3 3 A two-week-old panda bear Below Level Have students rename Advanced Learners Match up E, F, Inclusion 3 mixed numbers as improper fractions. G, and H to the digits 1, 2, 5, and 8 See note on page 191. weighed 4 pound. At age 2 = 3 2 5 to solve this mystery problem. Visual Learners one-month, the cub weighed 13 3 1 3 5 3 3 G F 9 2 10 pounds. How many pounds H 2 F 5 6 E ≠ 5, F ≠ 1, See note on page 192. 14 = 9 1 4 5 13 E G 10 did it gain? 111 lb 9 9 9 9 2 1 9 G ≠ 2, H ≠ 8 20 5 = 6 5 11 8 5 2 12 5 6 10 16 6 1 6 5 6 191 Visual Learners More Than One Way For the More Than One Way 1 feature, have students make a Suppose you caught two fish. The first one is 48 inches long. The second drawing to help them visualize 1 one is 2 inches long. How much longer is the first fish? the problem situation. Then work 4 through both solution methods Leon’s Method using colors to illustrate each step. For instance, have volunteers write 1 1 1 I need to subtract the lengths. Since , , I will rename 4 . the subtraction on the board or 8 4 8 an overhead transparency and use 1 9 1 1 9 4 3 d Rename 4 as 3 151 3 . a color to circle the denominators. 8 S 8 8 8 8 Then have students use another 1 2 1 2 2 2 2 4 d The LCD is 8. Write as . color to circle the numerators that 4 8 4 8 will be subtracted, and a third 7 1 d Find the difference. color for the number that has 8 been renamed. 7 The first fish is 1 8 inches longer than the second one. Closure Lauren’s Method • When do you have to rename when you are subtracting mixed I need to subtract the lengths. I will change both mixed numbers? when the fraction being subtracted is greater numbers to improper fractions with the same denominator. than the one from which it is 1 1 33 9 d 4 -=-2 Write as improper fractions. being subtracted 8 4 8 4 • Explain how you would rename =-33 18 d Rename as equivalent fractions 1 1 8 8 with a like denominator.
Load more

Recommended publications
  • Special-Sessions-1998-37941-600-21
    INTERNATIONAL OLYMPIC ACADEMY 6th INTERNATIONAL POST GRADUATE SEMINAR 1/5-12/6/1998 4th JOINT INTERNATIONAL SESSION FOR DIRECTORS OF NATIONAL OLYMPIC ACADEMIES, MEMBERS AND STAFF OF NATIONAL OLYMPIC COMMITTEES AND INTERNATIONAL SPORTS FEDERATIONS 7-14/5/1998 ANCIENT OLYMPIA ISBN: 960-8144-04-3 ISSN: 1108-6831 Published and edited by the International Olympic Academy. Scientific supervisor: Dr. Konstantinos Georgiadis/IOA Dean. Athens 2000 EPHORIA OF THE INTERNATIONAL OLYMPIC ACADEMY President Nikos FILARETOS (I.O.C. Member) 1st Vice-President Sotiris YAGAS t 2nd Vice-President Georgios MOISSIDIS Dean Konstantinos GEORGIADIS Member ex-officio Lambis NIKOLAOU (I.O.C. Member) Members Dimitris DIATHESSOPOULOS Georgios GEROLIMBOS Ioannis THEODORAKOPOULOS Epaminondas KIRIAZIS Cultural Consultant Panayiotis GRAVALOS Honorary President Juan Antonio SAMARANCH Honorary Vice-President Nikolaos YALOURIS 3 I.O.C. COMMISSION FOR THE INTERNATIONAL OLYMPIC ACADEMY AND OLYMPIC EDUCATION President Nikos FILARETOS IOC Member in Greece Vice-President Carol Ann LETHEREN IOC Member in Canada Members Fernando Ferreira Lima BELLO IOC Member in Portugal Valeriy BORZOV IOC Member in Ukraine Ivan DIBOS IOC Member in Peru Francis NYANGWESO IOC Member in Uganda Mohamed ZERGUINI IOC Member in Algeria Representatives George MOISSIDIS Fern. BELTRANENA VALLARADES Rene ROCH Representative of IFs Dieter LANDSBERG-VELEN Representative of IFs Philippe RIBOUD Representative of Athletes Individual Members Helen BROWNLEE (Australia) Conrado DURANTEZ (Spain) Yoon-bang KWON (Korea) Marc MAES (Belgium) Prof. Norbert MUELLER (Germany) 4 PROLOGUE The publication of the proceedings of the IOA's special ses- sions, for the second consecutive year, is one more contribution of the Ephoria of the Academy and the Hellenic Olympic Com- mittee to Olympism and Olympic Education.
    [Show full text]
  • Africathlète Août 2004
    Partenaires Officiels de la CAA Official AAC Partners 2 • africathlete - août 2004 Sommaire Contents Edito Citius, altius, fortius Jeux olympiques d’Athènes 2004 Que brillent les “ Etoiles “ d’Afrique ! Athens 2004 : Let african’s stars shine at athens olympic games ! 14e Championnat d’Afrique à Brazzaville L’Afrique du Sud en force, les performances au rendez-vous 14th African Championship in Brazzaville Performances galore as Shouth Africans rule the roost 15e championnat d’Afrique Rendez-vous à Maurice en 2006 African senior championships See you in Mauririus 2006 Circuit Africain des meetings Un véritable coup d’éclat African meet circuit : Is a remarkable feat Championnats du monde Juniors Les promesses de la jeune sève World junio championships : Africa’s promising young talents La confejes et la CAA à l’air du temp Confejes and CAA keep up with progress août 2004 - africathlete • 3 Editorial Citius, altius, fortius ’Afrique qui gagne, c’est bel et bien l’athlétisme. Vainqueur des quatre dernières éditions de la L Par/by Hamad Kalkaba Malboum Coupe du monde des Confédérations, l’Afrique peut Président de la CAA / AAC President aussi exhiber avec fierté ses multiples champions du monde, détenteurs de records du monde et cham- pions olympiques. Aucune discipline sportive, sur le continent, ne peut encore étaler un pareil palmarès. Et Citius, altius, fortius cerise sur le gâteau, les deux meilleurs athlètes du monde en 2003, en l’occurrence la Sud-Africaine frica is winning through athletics. In addition to win- Hestrie Cloete et le Marocain Hicham El Guerrouj, Aning the last four editions of the Confederations sont des fils de l’Afrique.
    [Show full text]
  • AFRREV STECH, Vol
    AFRREV STECH, Vol. 1 (2) April-July, 2012 AFRREV STECH An International Journal of Science and Technology Bahir Dar, Ethiopia Vol.1 (2) April-July, 2012:101-111 ISSN 2225-8612 (Print) ISSN 2227-5444 (Online) Sport as an Instrument for Social Cohesion in Nigeria Jeroh, Eruteyan Joseph, Ph.D. Department of Physical & Health Education, Delta State University, Abraka E-mail: [email protected] Phone: +2348038815809 Abstract The paper looked at the various roles sport could play in bringing about social cohesion in Nigeria. This was viewed from the perspective of benefits of sports to the society, schools, social significance of sports. The dark side of sport was also periscoped into. It was concluded that sport can provide opportunities to co-operate with others to achieve goals, make friends and straighten relationships with others, etc. It was recommended that governments from federal to local should encourage mass participation in sports by providing sports infrastructures nationwide. Physical and sport education should be mandatory at all levels of education. 101 Copyright © IAARR 2012: www.afrrevjo.net/stech AFRREV STECH, Vol. 1 (2) April-July, 2012 Key words: Meritocratric, Federal character, Chauvinists, Social transformation, Over-aged, Role Learning. Introduction From the onset, it might seem unnecessary defining sport because through experience and intuition most people already know what the word means. For the purpose of this discourse there is the need to know the meaning of sport as seen by many scholars. Loy (1978) claimed that sport must have five characteristics. It must: a) be play like in nature; b) involve some element of competition; c) be based on physical prowess; d) involve elements of skill, strategy, and chance; and e) have an uncertain outcome.
    [Show full text]
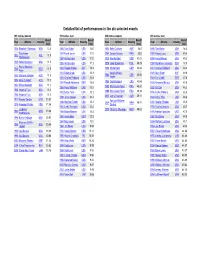
  • Detailed List of Performances in the Six Selected Events
    Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976
    [Show full text]
  • Africathlète Juillet 2004
    Partenaires Officiels de la CAA Official AAC Partners 2 • africathlete - juillet 2004 Sommaire Contents Editorial «Notre vision pour l’athlétisme africain» Editorial “Our vision for African athletics” 4 18e Congrès de la CAA : Les pistesdu 3e millénaire 18th AAC Congress : Charting the 3rd millennium 5-9 Lamine Diack passe le témoin à Hamad Kalkaba Lamine Diack hands over to Hamad Kalkaba 10 L’Afrique lance un circuit de 11 meetings Africa launches 11 meet circuit 11 Bienvenue à Brazzaville Welcome to Brazzaville 12 Calendrier Program 13-15 1ère rencontre Afrique-Europe en Septembre 2005 à Tanger Tangiers to host 1st Euro-African meet in September 2005 16 Les entraîneurs Africains dévoilent leurs ambitions African coaches reveal their ambitions 17 La CONFEJES soutient le CIAD CONFEJES supports CIAD 18 L’Afrique aux mondiaux de Paris : Mieux qu’à Edmonton World championships : Africa did better at Paris than at Edmonton 19-20 L’Afrique à la Coupe du monde : Le triomphe de l’esprit d’équipe Africa at the World Cup : A victory for team spirit 21-23 Etoiles d’Afrique Stars of Africa 24 Maria Mutola : Reine de la Golden League Maria Mutola : Queen of Golden League 25 Kenenisa Bekele détrône Gebrselassié Kenenisa Bekele supplants Gebrselassié 26 Records d’Afrique - Hommes Men Area Records - Africa 27 Records d’Afrique - Dames Women Area Records - Africa 28 Records du Monde - Hommes Men World Records 29 Records du Monde - Dames Women World Records 30 juillet 2004 - africathlete • 3 Editorial «Notre vision pour l’athlétisme africain» «Faire de l’athlétisme le sport le plus populaire, capable de promouvoir au sein de la jeunesse africaine les valeurs de solidarité et de performance, lui Par/by Hamad Kalkaba Malboum permettant de participer efficacement aux efforts de Président de la CAA / AAC President développement du continent», telle est notre vision pour l’athlétisme africain.
    [Show full text]
  • Argento - Bronzo
    OLIMPIADI L'Albo d'Oro delle Olimpiadi Atletica Leggera DONNE 100 METRI ANNO ORO - ARGENTO - BRONZO 2016 E. Thompson (JAM) 10”71, T. Bowie (USA) 10”83, S. A. Fraser (JAM) 10,86 2012 Shelly-Ann Fraser (JAM), Carmelita Jeter (USA), Veronica Campbell (JAM) 2008 Shelly-Ann Fraser (JAM), Sherone Simpson (JAM), Kerron Stewart (JAM) 2004 Yuliva Nesterenko (BLR), Lauryn Williams (USA), Veronica Campbell (JAM) 2000 vacante, Ekaterini Thanou (GRE), Tanya Lawrence (JAM), Merlene Ottey-Page (JAM) (Marion Jones (USA) squal.doping, 2 argenti 1 bronzo) 1996 Gail Devers (USA), Merlene Ottey (JAM), Gwen Torrence (USA) 1992 Gail Devers (USA), Juliet Cuthbert (JAM), Irina Privalova (CSI) 1988 Florence Griffith-Joyner (USA), Evelyn Ashford (USA), Heike Drechsler (GEE) 1984 Evelyn Ashford (USA), Alice Brown (USA), Merlene Ottey-Page (JAM) 1980 Lyudmila Kondratyeva (URS), Marlies Göhr (GEE), Ingrid Lange-Auerswald (GEE) 1976 Annegret Richter (GEO), Renate Stecher (GEE), Inge Helten (GEO) 1972 Renate Stecher (GEE), Raelene Boyle (AUS), Silvia Chivás (CUB) 1968 Wyomia Tyus (USA), Barbara Ferrell (USA), Irena Szewinska (POL) 1964 Wyomia Tyus (USA), Edith McGuire (USA), Ewa Klobukowska (POL) 1960 Wilma Rudolph (USA), Dorothy Hyman (GBR), Giuseppina Leone (ITA) 1956 Betty Cuthbert (AUS), Christa Stubnick (GER), Marlene Matthews (AUS) 1952 Marjorie Jackson (AUS), Daphne Hasenjäger (SAF), Shirley Strickland-de la Hunty (AUS) 1948 Fanny Blankers-Koen (OLA), Dorothy Manley (GBR), Shirley Strickland-de la Hunty (AUS) 1936 Helen Stephens (USA), Stanislawa Walasiewicz (POL), Käthe Krauss (GER) 1932 Stanislawa Walasiewicz (POL), Hilda Strike (CAN), Wilhelmina Van Bremen (USA 1928 Elizabeth Robinson (USA), Fanny Rosenfeld (CAN), Ethel Smith (CAN) 1896-1924 Non in programma 200 METRI ANNO ORO - ARGENTO - BRONZO 2016 E.
    [Show full text]
  • Answer All Questions in the Spaces Provided
    Practice Questions Level 3 Mathematical Studies 1350 Analysis of Data April 2018 F 2 1 The World Health Organisation (WHO) collects data and predicts the average life expectancy for someone born at a particular time in a particular country. The data below are for 193 countries and refer to the year 2009. The data have been organised into a grouped frequency table as shown below. Life expectancy at birth (L) Number of countries 45 ≤ L < 50 12 50 ≤ L < 60 24 60 ≤ L < 70 44 70 ≤ L < 75 53 75 ≤ L < 80 32 80 ≤ L < 85 28 (a) (i) On the grid below, draw a histogram for these data. L 40 50 60 70 80 90 Life expectancy at birth in 2009 (years) [4 marks] Version 1.0 1350/1 3 (ii) Using your histogram, or otherwise, estimate how many of these countries have a life expectancy at birth greater than 77 years. [2 marks] (b) (i) From the data given in the table above, estimate a value for the median life expectancy. [3 marks] (ii) For these data, the WHO gives the mean life expectancy for someone born in 2009 as 68 years. Explain why this differs from your median value found in part (b)(i). [1 mark] Version 0.4 1350/1 4 2 The table shows the winner and the length of the winning jump for the Olympic long jump between 1948 and 2012 Year Winner (Male) Country Length Winner (Female) Country Length (metres) (metres) 1948 Willie Steele USA 7.825 Olga Gyarmati HUN 5.695 1952 Jerome Biffle USA 7.57 Yvette Williams NZL 6.24 1956 Greg Bell USA 7.83 Elzbieta Krzeszinska POL 6.35 1960 Ralph Boston USA 8.12 Vera Krepkina URS 6.37 1964 Lynn Davies GBR 8.07 Mary Rand
    [Show full text]
  • 5000 Metres Walk
    ISTANBUL 2012 ★ NATIONAL INDOOR RECORDS/MEN 269 COUNTRY MARK NAME VENUE DATE COUNTRY MARK NAME VENUE DATE JPN 5600 Munehiro Kaneko Frankfurt-am-Main 11 Feb 96 TUN 5733 Hamdi Dhouibi Aubière 1 Mar 03 (7.18 – 6.88 – 13.97 – 1.80 / 8.24 – 4.90 – 2:43.05) (6.98 – 7.39 – 12.58 – 1.95 / 8.11 – 4.50 – 2:44.68) KAZ 6229 Dmitriy Karpov Tallinn 16 Feb 08 TUR 5612 Alper Kasapoğlu Monmout 2 Feb 97 (7.07 – 7.21 – 16.23 – 2.07 / 7.99 – 5.15 – 2:43.69) (7.19 – 7.00 – 13.07 – 1.88 / 8.13 – 4.46 – 2:50.72) KSA 5791 Mohammed Al-Qaree Hanoi 2 Nov 09 UKR 6254 Oleksiy Kasyanov Zaporizhzhya 31 Jan 10 (6.84 – 7.35 – 13.25 – 2.06 / 8.17 – 4.40 – 2:52.04) (6.85 – 8.04 – 15.15 – 2.05 / 8.18 – 4.70 – 2:42.88) KUW 4985 Mashari Zaki Mubarak Tehran 7 Feb 04 USA 6568 Ashton Eaton Tallinn 6 Feb 11 (7.09 – 6.46 – 12.67 – 1.90 / 8.30 – 4.00 – 3:11.10) (6.66 – 7.77 – 14.45 – 2.01 / 7.60 – 5.20 – 2:34.74) LAO 4069 Oudomsack Chanthavong Hanoi 2 Nov 09 UZB* 5918 Ramil Ganiyev Sofiya 25 Feb 90 (7.31 – 6.45 – 8.32 – 1.85 / 8.58 – 0 – 2:55.00) (7.12 – 7.26 – 14.20 – 2.15 / 8.22 – 4.70 – 2:49.51) LAT 5787 Edgars Eriņš Riga 23 Feb 08 VIE 5622 Vu Van Huyen Hanoi 2 Nov 09 (7.04 – 7.35 – 15.18 – 1.97 / 8.16 – 4.00 – 2:38.92) (6.96 – 7.18 – 11.64 – 2.00 / 8.43 – 4.60 – 2:45.52) LBR 5836 Janggy Addy Fayetteville 1 Mar 08 Notes (6.88 – 7.32 – 15.79 – 1.96 / 7.74 – 4.34 – 3:01.18) UZB 6031 Vadim Podmaryov (6.96 – 7.46 – 14.76 – 2.10 / 8.36 – 4.60 – LCA 5675 Dominic Johnson Manhattan 16 Jan 99 (7.13 – 6.90 – 12.79 – 2.06 / 8.47 – 4.70 – 2:42.22) 2:41.65) Zaporizhzhya 11 Feb 84 – Not recognised
    [Show full text]
  • Men's 400M Indoor World Athletics Indoor Tour 29.01.2021
    Men's 400m indoor World Athletics Indoor Tour 29.01.2021 Start list 400m ind. Time: 20:04 Records Lane Athlete Nat NR PB SB 1 Pavel MASLÁK CZE 45.24 45.24 WR 44.57 Kerron CLEMENT USA Fayetteville, AR 12.03.05 2Samuel GARCÍAESP45.6646.3546.98AR 45.05 Thomas SCHÖNLEBE GDR Sindelfingen 05.02.88 3 Óscar HUSILLOS ESP 45.66 45.66 =AR 45.05 Karsten WARHOLM NOR Glasgow 02.03.19 NR 45.05 Thomas SCHÖNLEBE GDR Sindelfingen 05.02.88 4 Yousef KARAM KUW 46.26 46.26 WJR 44.80 Kirani JAMES GRN Fayetteville, AR 27.02.11 5 Marvin SCHLEGEL GER 45.05 46.66 46.66 MR 46.11 Thomas SCHÖNLEBE GDR 11.02.90 SB 45.03 Fred KERLEY USA Fayetteville, AR 24.01.21 Medal Winners Previous Meeting 2021 World Indoor list 2019 - IAAF World Ch. in Athletics Winners 45.03 Fred KERLEY USA Fayetteville, AR (USA) 24.01.21 45.51 Matthew BOLING USA Columbia, SC (USA) 23.01.21 1. Steven GARDINER (BAH) 43.48 19 Pavel MASLÁK (CZE) 46.78 45.68 Bryce DEADMON USA College Station, TX (USA) 16.01.21 2. Anthony José ZAMBRANO (COL) 44.15 13 Michael SCHNEPF (GER) 51.66 45.73 Christopher TAYLOR JAM Fayetteville, AR (USA) 24.01.21 3. Fred KERLEY (USA) 44.17 12 Pavel MASLÁK (CZE) 46.29 46.23 Champion ALLISON USA Columbia, SC (USA) 23.01.21 11 Marcell DEÁK NAGY (HUN) 47.10 46.25 Travean CALDWELL USA Fayetteville, AR (USA) 24.01.21 2019 - European Indoor Ch.
    [Show full text]
  • Free-Standing Mathematics Qualification Preliminary Material
    Free-Standing Mathematics Qualification Advanced Level June 2014 Using and Applying 6990/2PM Statistics Unit 10 Preliminary Material Data Sheet To be opened and issued to candidates between Monday 28 April 2014 and Monday 5 May 2014 REMINDER TO CANDIDATES YOU MUST NOT BRING THIS DATA SHEET WITH YOU WHEN YOU SIT THE EXAMINATION. A CLEAN COPY WILL BE MADE AVAILABLE. P73043/Jun14/6990/2PM 6/6/6/6/ 6990/2PM 2 New homes How do British new-builds compare internationally? According to the government’s adviser on architecture, the UK builds the smallest homes in Europe. These are some of the complaints from residents of new-build developments surveyed by the Commission for Architecture and the Built Environment (CABE): The sofa won’t fit into the living room. There’s not enough room for children to play in the kitchen as you cook. Where’s the recycling bin meant to go? The floor area and room sizes are the smallest in Europe. The diagram below shows how British new-builds are less than half the size of those in the United States and Australia. Average total floor space of newly built homes (square metres) USA – 214 Australia – 206 Denmark – 137 Spain –97 UK –76 P73043/Jun14/6990/2PM 3 Earned income The table below shows the earned income declared by all taxpayers in the UK for the period 2009–2010. Total income, Self-employment including pension Employment income Range of total income and investment income (£) income No. of Amount No. of Amount No. of Amount individuals (£) individuals (£) individuals (£) 6 475 4 I < 10 000 662 4 220 2710 20 500 3700 30 700 10 000 4 I < 15 000 703 6 030 4200 47 600 6540 81 500 15 000 4 I < 20 000 513 5 930 4100 65 500 5450 94 800 20 000 4 I < 30 000 615 9 290 5610 126 000 6800 166 000 30 000 4 I < 50 000 494 10 300 4870 163 000 5490 208 000 50 000 4 I < 70 000 140 4 420 1190 60 300 1340 77 300 70 000 4 I < 100 000 92 4 550 538 37 100 621 51 000 100 000 4 I < 150 000 79 5 940 270 25 900 324 39 100 150 000 4 I 96 24 500 250 68 100 305 121 000 Key – All data for ‘Number of individuals’ are in thousands.
    [Show full text]
  • Sport As an Institution for Gender Stereotype Challenge and Women Empowerment: a Reflection on Nigerian Elite Sportswomen at the Olympics
    SPORT AS AN INSTITUTION FOR GENDER STEREOTYPE CHALLENGE AND WOMEN EMPOWERMENT: A REFLECTION ON NIGERIAN ELITE SPORTSWOMEN AT THE OLYMPICS Dr. Ifeanyichukwu C. Elendu and Dr. Tammy T. Orunaboka ABSTRACT This paper is a documental research based on literary review on the role of sport in challenging gender stereotype and serving as an institution for women empowerment in Nigeria. Women are always looking for how to address certain social issues and problems that affect them. Women empowerment is a social issue which women all over the world are clamoring for. Women have initiated and are still initiating movements geared towards ensuring that they have control over their socio-economic and political lives. Women have adopted several strategies including education to ensure that they achieve their goals. One of the strategies that could be used for women empowerment is sports. Sport is an empowerment avenue for all. Sport has also challenged gender stereotype that women are weak and inferior in social organizations. Among the areas that reflect one's empowerment are physical, economic, and social lives of the individuals. Sport empowers its participants including women physically by enhancing their strength, endurance, flexibility, power, agility; economically through salaries, match allowances as officiating officials and match commissioners, endorsement fees, and socially through interpersonal relationships, self-efficacy, friendship, among others. Among the challenges facing women empowerment through sports in Nigeria that were discussed include sexual harassment of women in sports; poor media coverage of women in sports; inadequate, substandard, and poor condition of sports facilities and equipment for women; poor funding of women's sports; inadequate motivation of women in sports; societal negative attitude towards women participation in sports, among others.
    [Show full text]
  • Lists N.2, All, 1998
    IAAF All Time World Indoor Lists 2 updated as at 7 March 2006 Compiled by Ottavio Castellini Legenda IAAF Statistics & Documentation Senior Manager A altitude h heat qf quarter-final sf semi-final f final Amendments will be gratefully received by r race Ottavio Castellini c competition (E-mail address : [email protected]) q qualification Tel. (+377) 93 10 88 72 = ex-aequo Fax (+377) 93 25 09 00 jo jump off jun junior Principality of Monaco, pen pentathlon 7 March 2006 hep heptathlon dec decathlon U20 Under 20 U23 Under 23 ope open ext extra Inv Invitational Uni University Col Collegiate HS High School * = world record awaiting ratification IAAF Statistics Office MEN MEN 50 Metres ( WR 5.56 Donovan Bailey CAN Reno, NV, 09 Feb 1996 ) 60 Metres ( WR 6.39 Maurice Greene USA Atlanta, GA, 03 Mar 2001 ) 5.56 A Donovan Bailey CAN 16 Dec 1967 1 Reno, NV 09 Feb 1996 6.45 A Leonard Myles-Mills GHA 09 May 1973 1 Colorado Springs, CO 20 Feb 1999 5.56 Maurice Greene USA 23 Jul 1974 1 Los Angeles, CA 13 Feb 1999 6.45 Maurice Greene 1 sf2 Maebashi 07 Mar 1999 5.58 Leonard Scott USA 19 Jan 1980 1+ Liévin 26 Feb 2005 6.45 Maurice Greene 1 New York, NY 04 Feb 2000 5.59 Maurice Greene 1+ Madrid 16 Feb 1999 6.45 A Terrence Trammell USA 23 Nov 1978 1 Pocatello, ID 17 Feb 2001 5.61 Manfred Kokot GDR 03 Jan 1948 1 h Berlin 04 Feb 1973 6.45 Justin Gatlin USA 10 Feb 1982 1 Boston (Rox), MA 01 Mar 2003 5.61 James Sanford USA 27 Dec 1957 1 San Diego, CA 20 Feb 1981 6.45 Ronald Pognon FRA 16 Nov 1982 1 Karlsruhe 13 Feb 2005 5.61 Michael Green JAM 07 Nov 1970 + Liévin
    [Show full text]