DOCSLIB.ORG

15.7 Introduction to Aromatic Compounds

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
15.7 Introduction to Aromatic Compounds 15_BRCLoudon_pgs5-0.qxd 12/9/08 12:22 PM Page 716 716 CHAPTER 15 • DIENES, RESONANCE, AND AROMATICITY PROBLEMS 15.27 In each of the following sets, show by the curved-arrow or fishhook notation how each reso- nance structure is derived from the other one, and indicate which structure is more important and why. .. .. (a) .. (b) .. C O.. C O H3CC| A NH H3CC ' NH| L 2 L carbon monoxide (c) (CH3)2CA CH CH| 2 (CH3)2C| CHA CH2 L L (d) N .. N C C CH3 CH3 15.28 Show the 2p orbitals, and indicate the orbital overlap symbolized by the resonance structures for the carbocation in Eq. 15.32 on p. 711. 15.29 Using resonance arguments, state which ion or radical within each set is more stable. Explain. (a) O _ O _ 332 332 H3C"CH CHA CH2 or H3C"C A CH CH3 L L L L (b) CH2 S A A A H2CCH CHCH CH8 2 or H2C8 C CH CH2 LL LL (c) CH3 H2CA"C CH| 2 or H3C CH A CH CH| 2 L L L 15.30 The following isomers do not differ greatly in stability. Predict which one should react more rapidly in an SN1 solvolysis reaction in aqueous acetone. Explain. H CH3 H CH2CH3 $CCA ) $CCA ) H3CCH CH)2 $H H3C CH) $H L L L "Cl "Cl AB 15.7 INTRODUCTION TO AROMATIC COMPOUNDS The term aromatic, as we’ll come to understand it in this section, is a precisely defined struc- tural term that applies to cyclic conjugated molecules that meet certain criteria. Benzene and its derivatives are the best known examples of aromatic compounds. H H "C H C C %S % # % or C "C r H C H % % ( % "H benzene 15_BRCLoudon_pgs5-0.qxd 12/9/08 12:22 PM Page 717 15.7 INTRODUCTION TO AROMATIC COMPOUNDS 717 The origin of the term aromatic is historical: many fragrant compounds known from earliest times, such as the following ones, proved to be derivatives of benzene. O S CHA O C OCH3 CH3 L A " " OH " H2C CH O % % i i i i OCH O % 3 OH methyl salicylate CH saffrole " (oil of wintergreen) " (oil of sassafras) H3C CH vanillin % % 3 (vanilla) p-cymene (cumin and thyme) Although it is known today that benzene derivatives are not distinguished by unique odors, the term aromatic—which has nothing to do with odor—has stuck, and it is now a class name for benzene, its derivatives, and a number of other organic compounds. Development of the theory of aromaticity was a major theoretical advance in organic chem- istry because it solved a number of intriguing problems that centered on the structure and reac- tivity of benzene. Before considering this theory, let’s see what some of these problems were. A. Benzene, a Puzzling “Alkene” The structure used today for benzene was proposed in 1865 by August Kekulé (p. 47), who claimed later that it came to him in a dream. The Kekulé structure portrays benzene as a cyclic, conjugated triene. Yet benzene does not undergo any of the addition reactions that are associ- ated with either conjugated dienes or ordinary alkenes. Benzene itself, as well as benzene rings in other compounds, are inert to the usual conditions of halogen addition, hydroboration, hydra- tion, or ozonolysis. This property of the benzene ring is illustrated by the addition of bromine to styrene, a compound that contains both a benzene ring and one additional double bond: CH A CH2 Br2 CH CH2 (15.38) cL + cL L "Br "Br styrene The noncyclic double bond in styrene rapidly adds bromine, but the benzene ring remains un- affected, even if excess bromine is used. This lack of alkenelike reactivity defined the unique- ness of benzene and its derivatives to early chemists. Does benzene’s lack of reactivity have something to do with its cyclic structure? Cyclo- hexene, however, adds bromine readily. Perhaps, then, it is the cyclic structure and the con- jugated double bonds that together account for the unusual behavior of benzene. However, 1,3,5,7-cyclooctatetraene (abbreviated in this text as COT) adds bromine smoothly even at low temperature. H 55 °C L " Br (15.39) Br2 L -CHCl3 H + Br 1,3,5,7-cyclooctatetraene (100% yield) (COT) 15_BRCLoudon_pgs5-0.qxd 12/9/08 12:22 PM Page 718 718 CHAPTER 15 • DIENES, RESONANCE, AND AROMATICITY Thus, the Kekulé structure clearly had difficulties that could not be easily explained away, but there were some ingenious attempts. In 1869, Albert Ladenburg proposed a structure for ben- zene, called both Ladenburg benzene and prismane, that seemed to overcome these objections. Ladenburg benzene or prismane Although Ladenburg benzene is recognized today as a highly strained molecule (it has been described as a “caged tiger”), an attractive feature of this structure to nineteenth-century chemists was its lack of double bonds. Several facts, however, ultimately led to the adoption of the Kekulé structure. One of the most compelling arguments was that all efforts to prepare the alkene 1,3,5-cyclohexatriene using standard alkene syntheses led to benzene. The argument was, then, that benzene and 1,3,5-cyclohexatriene must be one and the same compound. The reactions used in these routes received additional credibility because they were also used to prepare COT, which, as Eq. 15.39 illustrates, has the reactivity of an ordinary alkene. Although the Ladenburg benzene structure had been discarded for all practical purposes decades earlier, its final refutation came in 1973 with its synthesis by Professor Thomas J. Katz and his colleagues at Columbia University. These chemists found that Ladenburg ben- zene is an explosive liquid with properties that are quite different from those of benzene. How, then, can the Kekulé “cyclic triene” structure for benzene be reconciled with the fact that benzene is inert to the usual reactions of alkenes? The answer to this question will occupy our attention in the next three parts of this section. B. Structure of Benzene The structure of benzene is given in Fig. 15.10a. This structure shows that benzene has one type of carbon–carbon bond with a bond length (1.395 Å) that is the average the lengths of sp2–sp2 single bonds (1.46 Å) and double bonds (1.33 Å, Fig. 15.10c). All atoms in the benzene mole- cule lie in one plane. The Kekulé structure for benzene shows two types of carbon-carbon bond: single bonds and double bonds. This inadequacy of the Kekulé structure can be remedied, how- ever, by depicting benzene as the hybrid of two equally contributing resonance structures: 1.33 Å 1.395 Å 1.395 Å (15.40) 1.395ir Å 1.395 Å 1.46 Å Kekulé structure resonance hybrid Benzene is an average of these two structures; it is one compound with one type of carbon–carbon bond that is neither a single bond nor a double bond, but something in be- tween. A benzene ring is often represented with either of the following hybrid structures, which show the “smearing out” of double-bond character: ` ` hybrid structures of benzene 15_BRCLoudon_pgs5-0.qxd 12/9/08 12:22 PM Page 719 15.7 INTRODUCTION TO AROMATIC COMPOUNDS 719 H H H H 1.08 Å H 1.467 Å H C C 1.09 Å 120° 1.344 Å C C H 1.395 Å 122.9° 119.5° H H H H H 1,3-butadiene benzene (b) (a) HH CC1.09 Å H H C C 118.3° C 126.5° C H H 1.462 Å CC 1.334 Å H H 1,3,5,7-cyclooctatetraene (COT) ball-and-stick model of COT (c) (d) Figure 15.10 Comparison of the structures of benzene, 1,3-butadiene, and COT. (a) The structure of benzene. (“Double bonds” are not shown.) (b) The structure of 1,3-butadiene, a conjugated diene. (c) Structure of 1,3,5,7- cyclooctatetraene (COT). (d) A ball-and-stick model of COT. The carbon skeleton of benzene is a planar hexagon and all of the carbon–carbon bonds are equivalent with a bond length that is the average of the lengths of car- bon–carbon single and double bonds in COT. In contrast, COT has distinct single and double bonds with lengths that are almost the same as those in 1,3-butadiene, and COT is tub-shaped rather than planar. As with other resonance-stabilized molecules, we’ll continue to represent benzene as one of its resonance contributors because the curved-arrow notation and electronic bookkeeping de- vices are easier to apply to structures with fixed bonds. It is interesting to compare the structures of benzene and 1,3,5,7-cyclooctatetraene (COT) in view of their greatly different chemical reactivities (Eqs. 15.38 and 15.39). Their structures are remarkably different (Fig. 15.10). First, although benzene has a single type of carbon–car- bon bond, COT has alternating single and double bonds, which have almost the same lengths as the single and double bonds in 1,3-butadiene. Second, COT is not planar like benzene, but instead is tub-shaped. The p bonds of benzene and COT are also different (Fig. 15.11, p. 720). The Kekulé struc- tures for benzene suggest that each carbon atom should be trigonal, and therefore sp2-hy- bridized. This means each carbon atom has a 2p orbital (Fig. 15.11a). Because the benzene molecule is planar, and the axes of all six 2p orbitals of benzene are parallel, these 2p orbitals can overlap to form six p molecular orbitals.
Load more

Recommended publications
  • Analysis of Trace Hydrocarbon Impurities in 1,3-Butadiene Using Optimized Rt®-Alumina BOND/MAPD PLOT Columns by Rick Morehead, Jan Pijpelink, Jaap De Zeeuw, Tom Vezza
    Petroleum & Petrochemical Applications Analysis of Trace Hydrocarbon Impurities in 1,3-Butadiene Using Optimized Rt®-Alumina BOND/MAPD PLOT Columns By Rick Morehead, Jan Pijpelink, Jaap de Zeeuw, Tom Vezza Abstract Identifying and quantifying trace impurities in 1,3-butadiene is critical in producing high quality synthetic rubber products. Stan- dard analytical methods employ alumina PLOT columns which yield good resolution for low molecular weight hydrocarbons, but suffer from irreproducibility and poor sensitivity for polar hydrocarbons. In this study, Rt®-Alumina BOND/MAPD PLOT columns were used to separate both common light polar contaminants, including methyl acetylene and propadiene, as well as 4-vinylcy- clohexene, which is a high molecular weight impurity that normally requires a second test on an alternative column. By using an extended temperature program that employs the full thermal range of the column, 4-vinylcyclohexene, as well as all of the typical low molecular weight impurities in 1,3-butadiene, can be analyzed in a single test. Introduction 1,3-butadiene is typically isolated from products of the naphtha steam cracking process. Prior to purification, 1,3-butadiene can be contaminated with significant amounts of isobutene as well as other C4 isomers. In addition to removing these C4 isomeric contaminants during purification, it is also important that 1,3-butadiene be free of propadiene and methyl acetylene, which can interfere with catalytic polymerization. Alumina PLOT columns are the most commonly used GC column for this application, but the determination of polar hydrocarbon impurities at trace levels can be quite challenging and is highly dependent on the deactiva- tion of the alumina surface.
    [Show full text]
  • Transport of Dangerous Goods
    ST/SG/AC.10/1/Rev.16 (Vol.I) Recommendations on the TRANSPORT OF DANGEROUS GOODS Model Regulations Volume I Sixteenth revised edition UNITED NATIONS New York and Geneva, 2009 NOTE The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of any country, territory, city or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. ST/SG/AC.10/1/Rev.16 (Vol.I) Copyright © United Nations, 2009 All rights reserved. No part of this publication may, for sales purposes, be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, electrostatic, magnetic tape, mechanical, photocopying or otherwise, without prior permission in writing from the United Nations. UNITED NATIONS Sales No. E.09.VIII.2 ISBN 978-92-1-139136-7 (complete set of two volumes) ISSN 1014-5753 Volumes I and II not to be sold separately FOREWORD The Recommendations on the Transport of Dangerous Goods are addressed to governments and to the international organizations concerned with safety in the transport of dangerous goods. The first version, prepared by the United Nations Economic and Social Council's Committee of Experts on the Transport of Dangerous Goods, was published in 1956 (ST/ECA/43-E/CN.2/170). In response to developments in technology and the changing needs of users, they have been regularly amended and updated at succeeding sessions of the Committee of Experts pursuant to Resolution 645 G (XXIII) of 26 April 1957 of the Economic and Social Council and subsequent resolutions.
    [Show full text]
  • An Empirical Formula Expressing the Mutual Dependence of C-C Bond Distances* Arpad Furka Department of Organic Chemistry Eotvos Lorcind University, Muzeum Krt
    CROATICA CHEMICA ACTA CCACAA 56 (2) 191-197 (1983) YU ISSN 0011-1643 CCA-1368 UDC 547 :541.6 Originai Scientific Paper An Empirical Formula Expressing the Mutual Dependence of C-C Bond Distances* Arpad Furka Department of Organic Chemistry Eotvos Lorcind University, Muzeum krt. 4/B Budapest, 1088, Hungary Received August 30, 1982 An empirical formula is suggested to describe the mutuaJ dependence of the length of the bonds formed by a central atom in systems built up from equivalent carbon atoms, e.g. diamond, graphite, the cumulene and polyyne chains and intermediate struc­ tures between them. A geometrical representation of the relation­ ship is a regular tetrahedron. A point of this tetrahedron charac­ terizes the arrangement of the atoms around the central one. From the position of the point the bond distances - and possibly the bond angles - can be deduced. Experimental bond length determinations have made clear in the last few decades that the C-C bond distances vary over a relatively long range, from about 1.2 A to about 1.6 A. There were several attempts to correlate these bond distances on empirical way to different factors like double-bond 1 2 4 character, • n:-bond order,3 state of hybridization, •5 the number of adjacent bonds,6 or the overlap integrals.7 Recently ·a new empirical formula has been suggested to describe the mutual dependence of the C-C bond distances.8 The subject of this paper is the interpretation of this empirical equation. Carbon has three allotropic modifications: diamond, graphite and the not completely characterized chain form9•10 (carbynes).
    [Show full text]
  • Unusual Ring Opening of Hexamethyl Dewar Benzene in Its Reaction with Triosmium Carbonyl Cluster
    Organometallics 2003, 22, 2361-2363 2361 Unusual Ring Opening of Hexamethyl Dewar Benzene in Its Reaction with Triosmium Carbonyl Cluster Wen-Yann Yeh* and Yu-Chiao Liu Department of Chemistry, National Sun Yat-Sen University, Kaohsiung, Taiwan 804 Shie-Ming Peng and Gene-Hsiang Lee Department of Chemistry, National Taiwan University, Taipei, Taiwan 106 Received April 15, 2003 6 Summary: Os3(CO)10(NCMe)2 catalyzes the transforma- HMDB produces the HMB complex [(η -C6Me6)Fe- 11 tion of hexamethyl Dewar benzene (HMDB) to hexameth- (CO)2]2. In rare cases the HMDB moiety has lost its ylbenzene (HMB). This catalytic reaction is in competi- unity, such as in the reaction of RhCl3‚xH2O with 5 tion with ring opening of the HMDB ligand to give (µ- HMDB, causing a ring contraction to give [(η -C5Me5)- 3 12 H)2Os3(CO)9(µ-η -CH(C6Me5)) (1) and (µ-H)Os3(CO)9(µ3- RhCl2]2. However, the coordination chemistry of HMDB 2 t η -C C(C4Me4Et)) (2). with metal clusters has received little attention. We now The coordination chemistry of strained hydrocarbons report that Os3(CO)10(NCMe)2 not only catalyzes the has fascinated chemists striving to understand the conversion of HMDB to HMB but also causes unusual - - details of structure and reactivity.1 In particular, ben- C H and C C bond activations of the HMDB ligand to zene is rich with high-energy strained isomers, such as form unique cluster complexes. Dewar benzene, prismane, and benzvalene, which in- Treatment of Os3(CO)10(NCMe)2 with HMDB (4-fold) terconvert through complex and mysterious rearrange- at
    [Show full text]
  • Brittain-DR-1965-Phd-Thesis.Pdf
    POLYMETHYLENE PYRIDINES , A thesis submitted by David Robert Brittain in partial fulfilment of the requirements for the degree of DOCTOR OP PHILOSOPHY in the University of London Organic Chemistry Department, dune, 1965. Imperial College, LONDON, S.W.7. ABSTRACT This thesis describes a series of attempts to syn- thesise 2,5- and 1,4-polymethylene bridged pyridines. Nuclear magnetic resonance theory predicts that protons, which are held directly over an aromatic ring, will be abnormally shielded compared with protons in aliphatic straight-chain hydrocarbons. This prediction has been verified for the central methylene protons of paracyclo- phanes. The degree of shielding, expressed in terms of the distance from the aromatic ring, is a measure of the induced ring current and hence the aromaticity of the benzene ring. Similar measurements upon 2,5- or 1,4— polymethylene bridged pyridines would make it possible to determine the degree of aromaticity of the pyridine ring relative to benzene. A review of the subject of aromaticity is presented in which special reference has been made to its inter- pretation by nuclear magnetic resonance. The synthetic work has not been brougL.t to a truly satisfactory conclusion. However, the synthetic routes to 2,5-dialkylpyridines have been thoroughly investigated and a wide variety of such compounds prepared. The functional groups at the ends of the alkyl chains have been varied in an effort to produce a derivative which would cyclise to give a 2,5-bridged pyridine. The attempted intramolecular oxidative coupling of 2,5-dihex- 51 -ynylpyridine received much attention. In the attempts to obtain a 1,4-bridged pyridine, two tricyclic compounds, each containing two quaternised pyridine rings linked by polymethylene chains, were obtained.
    [Show full text]
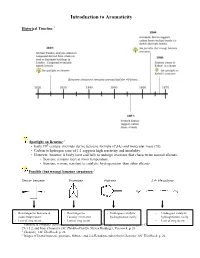
  • Introduction to Aromaticity
    Introduction to Aromaticity Historical Timeline:1 Spotlight on Benzene:2 th • Early 19 century chemists derive benzene formula (C6H6) and molecular mass (78). • Carbon to hydrogen ratio of 1:1 suggests high reactivity and instability. • However, benzene is fairly inert and fails to undergo reactions that characterize normal alkenes. - Benzene remains inert at room temperature. - Benzene is more resistant to catalytic hydrogenation than other alkenes. Possible (but wrong) benzene structures:3 Dewar benzene Prismane Fulvene 2,4- Hexadiyne - Rearranges to benzene at - Rearranges to - Undergoes catalytic - Undergoes catalytic room temperature. Faraday’s benzene. hydrogenation easily. hydrogenation easily - Lots of ring strain. - Lots of ring strain. - Lots of ring strain. 1 Timeline is computer-generated, compiled with information from pg. 594 of Bruice, Organic Chemistry, 4th Edition, Ch. 15.2, and from Chemistry 14C Thinkbook by Dr. Steven Hardinger, Version 4, p. 26 2 Chemistry 14C Thinkbook, p. 26 3 Images of Dewar benzene, prismane, fulvene, and 2,4-Hexadiyne taken from Chemistry 14C Thinkbook, p. 26. Kekulé’s solution: - “snake bites its own tail” (4) Problems with Kekulé’s solution: • If Kekulé’s structure were to have two chloride substituents replacing two hydrogen atoms, there should be a pair of 1,2-dichlorobenzene isomers: one isomer with single bonds separating the Cl atoms, and another with double bonds separating the Cl atoms. • These isomers were never isolated or detected. • Rapid equilibrium proposed, where isomers interconvert so quickly that they cannot be isolated or detected. • Regardless, Kekulé’s structure has C=C’s and normal alkene reactions are still expected. - But the unusual stability of benzene still unexplained.
    [Show full text]
  • On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and Its Application to Heteroatomic Π-Electron Systems
    Symmetry 2010, 2, 1485-1509; doi:10.3390/sym2031485 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and its Application to Heteroatomic π-Electron Systems Ewa D. Raczyñska 1, *, Małgorzata Hallman 1, Katarzyna Kolczyñska 2 and Tomasz M. Stêpniewski 2 1 Department of Chemistry, Warsaw University of Life Sciences (SGGW), ul. Nowoursynowska 159c, 02-776 Warszawa, Poland 2 Interdisciplinary Department of Biotechnology, Warsaw University of Life Sciences (SGGW), ul. Nowoursynowska 166, 02-776 Warszawa, Poland * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +48-22-59-37623; Fax: +49-22-59-37635. Received: 23 April 2010; in revised form: 19 May 2010 / Accepted: 7 July 2010 / Published: 12 July 2010 Abstract: The HOMA (Harmonic Oscillator Model of Aromaticity) index, reformulated in 1993, has been very often applied to describe π-electron delocalization for mono- and polycyclic π-electron systems. However, different measures of π-electron delocalization were employed for the CC, CX, and XY bonds, and this index seems to be inappropriate for compounds containing heteroatoms. In order to describe properly various resonance effects (σ-π hyperconjugation, n-π conjugation, π-π conjugation, and aromaticity) possible for heteroatomic π-electron systems, some modifications, based on the original HOMA idea, were proposed and tested for simple DFT structures containing C, N, and O atoms. An abbreviation HOMED was used for the modified index. Keywords: geometry-based index; π -electron delocalization; σ - π hyperconjugation; n-π conjugation; π-π conjugation; aromaticity; heteroatomic compounds; DFT 1.
    [Show full text]
  • Conversion of Methoxy and Hydroxyl Functionalities of Phenolic Monomers Over Zeolites Rajeeva Thilakaratne Iowa State University
    Chemical and Biological Engineering Publications Chemical and Biological Engineering 2016 Conversion of methoxy and hydroxyl functionalities of phenolic monomers over zeolites Rajeeva Thilakaratne Iowa State University Jean-Philippe Tessonnier Iowa State University, [email protected] Robert C. Brown Iowa State University, [email protected] Follow this and additional works at: https://lib.dr.iastate.edu/cbe_pubs Part of the Biomechanical Engineering Commons, and the Catalysis and Reaction Engineering Commons The ompc lete bibliographic information for this item can be found at https://lib.dr.iastate.edu/ cbe_pubs/328. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Article is brought to you for free and open access by the Chemical and Biological Engineering at Iowa State University Digital Repository. It has been accepted for inclusion in Chemical and Biological Engineering Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Conversion of methoxy and hydroxyl functionalities of phenolic monomers over zeolites Abstract This study investigates the mechanisms of gas phase anisole and phenol conversion over zeolite catalyst. These monomers contain methoxy and hydroxyl groups, the predominant functionalities of the phenolic products of lignin pyrolysis. The proposed reaction mechanisms for anisole and phenol are distinct, with significant differences in product distributions. The nia sole mechanism involves methenium ions in the conversion of phenol and alkylating aromatics inside zeolite pores. Phenol converts primarily to benzene and naphthalene via a ring opening reaction promoted by hydroxyl radicals. The hep nol mechanism sheds insights on how reactive bi-radicals generated from fragmented phenol aromatic rings (identified as dominant coke precursors) cyclize rapidly to produce polyaromatic hydrocarbons (PAHs).
    [Show full text]
  • Aromaticity Sem- Ii
    AROMATICITY SEM- II In 1931, German chemist and physicist Sir Erich Hückel proposed a theory to help determine if a planar ring molecule would have aromatic properties .This is a very popular and useful rule to identify aromaticity in monocyclic conjugated compound. According to which a planar monocyclic conjugated system having ( 4n +2) delocalised (where, n = 0, 1, 2, .....) electrons are known as aromatic compound . For example: Benzene, Naphthalene, Furan, Pyrrole etc. Criteria for Aromaticity 1) The molecule is cyclic (a ring of atoms) 2) The molecule is planar (all atoms in the molecule lie in the same plane) 3) The molecule is fully conjugated (p orbitals at every atom in the ring) 4) The molecule has 4n+2 π electrons (n=0 or any positive integer Why 4n+2π Electrons? According to Hückel's Molecular Orbital Theory, a compound is particularly stable if all of its bonding molecular orbitals are filled with paired electrons. - This is true of aromatic compounds, meaning they are quite stable. - With aromatic compounds, 2 electrons fill the lowest energy molecular orbital, and 4 electrons fill each subsequent energy level (the number of subsequent energy levels is denoted by n), leaving all bonding orbitals filled and no anti-bonding orbitals occupied. This gives a total of 4n+2π electrons. - As for example: Benzene has 6π electrons. Its first 2π electrons fill the lowest energy orbital, and it has 4π electrons remaining. These 4 fill in the orbitals of the succeeding energy level. The criteria for Antiaromaticity are as follows: 1) The molecule must be cyclic and completely conjugated 2) The molecule must be planar.
    [Show full text]
  • 1 5. Chemical Bonding
    5. Chemical Bonding: The Covalent Bond Model 5.1 The Covalent Bond Model Almost all chemical substances are found as aggregates of atoms in the form of molecules and ions produced through the reactions of various atoms of elements except the noble-gas elements which are stable mono-atomic gases. Chemical bond is a term that describes the attractive force that is holding the atoms of the same or different kind of atoms in forming a molecule or ionic solid that has more stability than the individual atoms. Depending on the kinds of atoms participating in the interaction there seem to be three types of bonding: Gaining or Losing Electrons: Ionic bonding: Formed between many ions formed by metal and nonmetallic elements. Sharing Electrons: Covalent bonding: sharing of electrons between two atoms of non-metals. Metallic Bonding: sharing of electrons between many atoms of metals. Ionic Compounds Covalent Compounds Metallic Compounds 1. Metal and non-meal Non-metal and non-meal Metal of one type or, element combinations. elements combinations. combinations of two or metal elements combinations. 2. High melting brittle Gases, liquids, or waxy, low Conducting, high melting, crystalline solids. melting soft solids. malleable, ductile crystalline solids. 3. Do not conduct as a solid Do not conduct electricity at Conduct electricity at solid but conducts electricity any state. and molten states. when molten. 4. Dissolved in water produce Most are soluble in non-polar Insoluble in any type of conducting solutions solvents and few in water. solvents. (electrolytes) and few These solutions are non- are soluble in non-polar conducting (non- solvents.
    [Show full text]
  • Prismane Structure by Silicon Substitution†
    J. Chem. Sci. Vol. 129, No. 7, July 2017, pp. 911–917. © Indian Academy of Sciences. DOI 10.1007/s12039-017-1264-8 REGULAR ARTICLE Special Issue on THEORETICAL CHEMISTRY/CHEMICAL DYNAMICS Stabilisation of the [6]-prismane structure by silicon substitution† ASIF EQUBALa, SHWETHA SRINIVASANa and NARAYANASAMI SATHYAMURTHYa,b,∗ aDepartment of Chemical Sciences, Indian Institute of Science Education and Research (IISER) Mohali, Sector 81, SAS Nagar, Manauli, 140 306, India bDepartment of Chemistry, Indian Institute of Technology Kanpur, Kanpur, 208 016, India E-mail: [email protected] MS received 9 January 2017; revised 6 March 2017; accepted 17 March 2017 Abstract. Using the second-order Møller–Plesset perturbation (MP2) theoretic method and the cc-pVDZ basis set, it is shown that with an increase in the number of carbon atoms substituted by silicon, the [6]-prismane structure becomes increasingly more stable, relative to the two isolated benzene (like) structures. A similar trend is observed for germanium substituted prismanes as well. Extending this investigation, the stability of benzene-capped fullerene (C60 fused with benzene) is also investigated. Keywords. [6]-Prismane; silabenzene; germanobenzene; benzene-capped fullerene. 1. Introduction readily achieved, 22–25 synthesis of [6]-prismane remained a challenge until Mehta and Padma 26,27 came up with Benzene is known to be highly stable. The interaction of a novel idea to synthesize it using Diels-Alder addi- two benzene molecules has been investigated over the tion and photocatalysis. [6]-Prismane has the structure years, and the parallel displaced and T-shaped geome- of a regular hexagonal prism wherein two parallel 6- tries have been shown to be comparable in stability from membered rings are co-joined face-to-face resulting a theoretical point of view.
    [Show full text]
  • Chemical Forces Understanding the Relative Melting/Boiling Points of Two
    Chapter 8 – Chemical Forces Understanding the relative melting/boiling points of two substances requires an understanding of the forces acting between molecules of those substances. These intermolecular forces are important for many additional reasons. For example, solubility and vapor pressure are governed by intermolecular forces. The same factors that give rise to intermolecular forces (e.g. bond polarity) can also have a profound impact on chemical reactivity. Chemical Forces Internuclear Distances and Atomic Radii There are four general methods of discussing interatomic distances: van der Waal’s, ionic, covalent, and metallic radii. We will discuss the first three in this section. Each has a unique perspective of the nature of the interaction between interacting atoms/ions. Van der Waal's Radii - half the distance between two nuclei of the same element in the solid state not chemically bonded together (e.g. solid noble gases). In general, the distance of separation between adjacent atoms (not bound together) in the solid state should be the sum of their van der Waal’s radii. F F van der Waal's radii F F Ionic Radii – Ionic radii were discussed in Chapter 4 and you should go back and review that now. One further thing is worth mentioning here. Evidence that bonding really exists and is attractive can be seen in ionic radii. For all simple ionic compounds, the ions attain noble gas configurations (e.g. in NaCl the Na+ ion is isoelectronic to neon and the Cl- ion is isoelectronic to argon). For the sodium chloride example just given, van der Waal’s radii would predict (Table 8.1, p.
    [Show full text]