DOCSLIB.ORG

DOCUMENT RESUME Olivier, Alwyn

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
DOCUMENT RESUME Olivier, Alwyn DOCUMENT RESUME ED 427 970 SE 062 272 AUTHOR Olivier, Alwyn, Ed.; Newstead, Karen, Ed. TITLE Proceedings of the Conference of the International Group for the Psychology of Mathematics Education (22nd, Stellenbosch, South Africa, July 12-17, 1998) .Volume 2. INSTITUTION International Group for the Psychology of Mathematics Education. ISSN ISSN-0771-100X PUB DATE 1998-00-00 NOTE 360p.; For volumes 1-4, see SE 062 271-274; for the 1998 conference, see ED 416 082-085. PUB TYPE Collected Works - Proceedings (021) EDRS PRICE MF01/PC15 Plus Postage. DESCRIPTORS Algebra; *Beliefs; Cultural Influences; Data Processing; Educational Change; Educational Research; Educational Technology; Elementary Secondary Education; Foreign Countries; Fractions; Functions (Mathematics); Geometry; Knowledge Base for Teaching; Learning Theories; *Mathematics Education; Number Concepts; *Problem Solving; Proof (Mathematics); *Social Influences; Spatial Ability; Statistics; *Student Attitudes; Teacher Education; Thinking Skills ABSTRACT The second volume of this proceedings contains the first portion of the research reports. Papers include: (1) "Learning Algebraic Strategies Using a Computerized Balance Model" (James Aczel); (2) "Children's Perception of Multiplicative Structure in Diagrams" (Bjornar Alseth); (3) "A Discussion of Different Approaches to Arithmetic Teaching" (Julia Anghileri); (4) "A Model for Analyzing the Transition to Formal Proofs in Geometry" (Ferdinando Arzarello, Chiara Micheletti, Federica Olivero, Ornella Robutti, and Domingo Paola);(5) "Dragging in Cabri and Modalities of Transition from Conjectures to Proofs in Geometry" (Ferdinando Arzarello, Chiara Micheletti, Federica Olivero, Ornella Robutti, Domingo Paola, and Gemma Gallino); (6) "The Co-Construction of Mathematical Knowledge: The Effect of an Intervention Program on Primary Pupils' Attainment" (Mike Askew, Tamara Bibby, and Margaret Brown); (7) "Dialectical Proof: Should We Teach It to Physics Students?" (Roberto Ribeiro Baldino); (8) "Lacan and the School's Credit System" (Roberto Ribeiro Baldino and Tania Cristina Baptista Cabral); (9) "Which Is the Shape of an Ellipse? A Cognitive Analysis of an Historical Debate" (Maria G. Bartolini Bussi and Maria Alessandra Mariotti); (10) "Children's Understanding of the Decimal Numbers through the Use of the Ruler" (Milena Basso, Cinzia Bonotto, and Paolo Sozio);(11) "Construction of Multiplicative Abstract Schema for Decimal-Number Numeration" (Annette R. Baturo and Tom J. Cooper);(12) "Classroom-Based Research to Evaluate a Model Staff Development Project in Mathematics" (Joanne Rossi Becker and Barbara J. Pence); (13) "Some Misconceptions Underlying First-Year Students' Understanding of 'Average Rate' and of 'Average Value'" (Jan Bezuidenhout, Piet Human, and Alwyn Olivier);(14) "Operable Definitions in Advanced Mathematics: The Case of the Least Upper Bound" (Liz Bills and David Tall); (15) "Beyond 'Street' Mathematics: The Challenge of Situated Cognition" (Jo Boaler); (16) "The 'Voices and Echoes Game' and the Interiorization of Crucial Aspects of Theoretical Knowledge in a Vygotskian Perspective: Ongoing +++++ ED427970 Has Multi-page SFR---Level=1 +++++ Research" (Paolo Boero, Bettina Pedemonte, Elisabetta Robotti, and Giampaolo Chiappini); (17) "Children's Construction of Initial Fraction Concepts" (George Booker);(18) "Graphing Calculators and Reorganization of Thinking: The Transition from Functions to Derivative" (Marcelo C. Borba and Monica E. Villarreal);(19) "Pre-Algebra: A Cognitive Perspective" (G.M. Boulton-Lewis, T. Cooper, B. Atweh, H. Pillay, and L. Wilss);(20)"The Right Baggage?" (Mary Briggs);(21) "Learner-Centered Teaching and Possibilities for Learning in South African Mathematics Classrooms" (Karin Brodie); (22) "Researching Transition in Mathematical Learning" (Tony Brown, Frank Eade, and Dave Wilson);(23) "Metaphor as Tool in Facilitating Preservice Teacher Development in Mathematical Problem Solving" (Olive Chapman); (24) "Restructuring Conceptual and Procedural Knowledge for Problem Representation" (Mohan Chinnappan); (25) "The Structure of Students' Beliefs towards the Teaching of Mathematics: Proposing and Testing a Structural Model" (Constantinos Christou and George N. Philippou); (26) "Abstract Schema versus Computational Proficiency in Percent Problem Solving" (Tom J. Cooper, Annette R. Baturo, and Shelley Dole);(27) "Implicit Cognitive Work in Putting Word Problems into Equation Form" (Anibal Cortes);(28) "Three Sides Equal Means It Is Not Isosceles" (Penelope Currie and John Pegg); (29) "Making Sense of Sine and Cosine Functions through Alternative Approaches: Computer and 'Experimental World' Contexts" (Nielce Lobo Da Costa and Sandra Magina);(30) "Teacher and Students' Flexible Thinking in Mathematics: Some Relations" (Maria Manuela M.S. David and Maria da Penha Lopes);(31) "The Influence of Metacognitive and Visual Scaffolds on the Predominance of the Linear Model" (Dirk De Bock, Lieven Verschaffel, and Dirk Janssens); (32)"To Teach Definitions in Geometry or Teach To Define?" (Michael De Villiers); (33) "Student thinking about Models of Growth and Decay" (Helen M. Doerr); (34) "Analysis of a Long Term Construction of the Angle Concept in the Field of Experience of Sunshadows" (Nadia Douek);(35) "On Verbal Addition and Subtraction in Mozambican Bantu Languages" (Jan Draisma);(36) "Teachers' Beliefs and the 'Problem' of the Social" (Paula Ensor);(37) "From Number Patterns to Algebra: A Cognitive Reflection on a Cape Flats Experience" (Clyde B.A. Felix); (38)"Affective Dimensions and Tertiary Mathematics Students" (Helen J. Forgasz and Gilah C. Leder);(39) "Social Class Inequalities in Mathematics Achievement: A Multilevel Analysis of T1MSS South Africa Data" (George Frempong); (40) "Context Influence on Mathematical Reasoning" (Fulvia Furinghetti and Domingo Paola); (41) "What Do They Really Think? What Students Think about the Median and Bisector of an Angle in the Triangle, What They Say and What Their Teachers Know about It" (Hagar Gal); (42) "Levels of Generalization in Linear Patterns" (Juan Antonio Garcia-Cruz and Antonio Martinon); (43) "The Evolution of Pupils' Ideas of Construction and Proof Using Hand-Held Dynamic Geometry Technology" (John Gardiner and Brian Hudson); and (44) "Cognitive Unity of Theorems and Difficulty of Proof" (Rosella Garuti, Paolo Boero, and Enrica Lemut). (ASK) ******************************************************************************** Reproductions supplied by EDRS are the best that can be made from the original document. ******************************************************************************** alb Mb U S DEPARTMENT OF EDUCATION Office of Educahonal Research and Improvement EDUCATIONAL RESOURCES INFORMATION CENTER (ERIC) This document has been reproduced,as 1 awed from the person or organization originating it PERMISSION TO REPRODUCE AND O Minor changes have been made to DISSEMINATETHIS MATERIAL HAS improve reproduction quality BEEN GRANTED BY Points of view or opinions stated in this document do not necessarily represent official OERI position or policy TO THE EDUCATIONAL RESOURCES INFORMATION CENTER (ERIC) 1 k 1247 July 1998 \1%11tItosch, southAl%41 BEST COPY AVAILABLE - - Proceedings of the 22nd Conference of the International Group for the PsyChology of Mathematics Education Volume 2 Editors: Alwyrraiutérand Karen Newstead University of Si&enbosch Stellenbosch, South Africa BEST COPY AVAILABLE 1998 Proceedings of the 22nd Conference of the International Group for the Psychology of Mathematics Education Volume 2 Published by the Program Committee of the 22nd PME Conference. Stellenbosch, South Africa Editors: Alwyn Olivier and Karen Newstead Faculty of Education The University of Stellenbosch Stellenbosch South Africa 7600 Fax: +27 21 887 2616 E-mail: [email protected] © Copyright 1998 left to the individual authors ISSN 0771-100X Printed by Kwik Kopy Printing Bellville, South Africa 2 - ii CONTENTS OF VOLUME 2 Research Reports Aczel, James 2-1 Learning algebraic strategies using a computerised balance model Alseth, Bjornar 2-9 Children's perception of multiplicative structure in diagrams Anghileri, Julia 2-17 A discussion of different approaches to arithmetic teaching Arzarello. Ferdinando; Micheletti, Chiara; Olivero, Federica; Robutti, Omella & Paola, Domingo 2-24 A model for analysing the transition to formal proofs in geometry Arzarello, Ferdinando; Micheletti, Chiara; Olivero. Federica; Robutti, Ornella; Paola, Domingo & Gallino, Gemma 2-32 Dragging in Cabri and modalities of transition from conjectures to proofs in geometry akeLvAElie; Bibby, Tamara & Brown, Margaret 2-40 The co-construction of mathematical knowledge: The effect of an intervention programme on primary pupils' attainment Baldino, Roberto Ribeiro 2-48 Dialectical proof: Should we teach it to physics students? Baldino, Roberto Ribeiro & Cabral. Tânia Cristina Baptista 2-56 Lacan and the school's credit system Bartolini Bussi. Maria G, & Mariotti, Maria Alessandra 2-64 Vl/hich is the shape of an ellipse? A cognitive analysis of an historical debate Basso, Milena; Bonotto, Cinzia & Sorzio. Paolo 2-72 Children's understanding of the decimal numbers through the use of the ruler Baturo. Annette R. & Cooper, Tom J. 2-80 Construction of multiplicative abstract schema for decimal-number numeration Becker. Joanne Rossi & Pence, Barbara J. 2-88 Classroom-based research to evaluate a model staff development project in mathematics Bezuidenhout. Jan; Human, Piet & Olivier, Alwyn 2-96
Load more

Recommended publications
  • Lexus Listening Lounge Returns to the Chicago Auto Show Featuring Legendary Peformers & Chicago Favorites
    PRESS INFORMATION LEXUS LISTENING LOUNGE RETURNS TO THE CHICAGO AUTO SHOW FEATURING LEGENDARY PEFORMERS & CHICAGO FAVORITES Special Edition of The Lexus Listening Lounge Will Feature PJ Morton, Jon B, Angie Fisher and More (CHICAGO) February 1, 2017 – Leading luxury automotive brand Lexus announces its return to the Chicago Auto Show with a special edition of its hit R&B/Soul music property, the Lexus Listening Lounge from Saturday, February 11 through Sunday, February 19. Lexus has been tapped once again to provide a special guest at the exclusive First Look for Charity Gala. Auto show attendees will have the opportunity to view the all-new 2018 LS 500, as well as the full line-up offered by Lexus and be treated to amazing live performances and meet-and- greets with guest performers. Along with Grammy-nominated and award-winning artists, returning to the stage this year will also be some familiar faces and up-and-coming Chicago talent. This stellar lineup includes: Jon B, PJ Morton, Syleena Johnson, Angie Fisher, Krystal Metcalfe and The Moe Fitz Project. The schedule for the Lexus Listening Lounge at the Chicago Auto Show includes: Friday, February 10, 2017 (PRIVATE CHARITY PERFORMANCE) PJ Morton Performance: 7:00 PM – 7:30 PM As his celebrated 2015 live album Live Show Killer suggests, PJ Morton’s heart is onstage. In fact, the indie R&B darling and Maroon 5 keyboardist/vocalist owes his loyal following as much to his electrifying shows as to his popular albums. Influenced by acts ranging from the Beatles and James Taylor to Stevie Wonder and Donny Hathaway, the New Orleans native is the son of gospel singer Paul S.
    [Show full text]
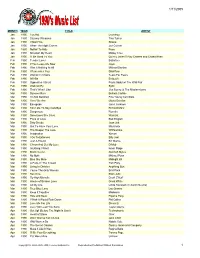
  • 1990S Playlist
    1/11/2005 MONTH YEAR TITLE ARTIST Jan 1990 Too Hot Loverboy Jan 1990 Steamy Windows Tina Turner Jan 1990 I Want You Shana Jan 1990 When The Night Comes Joe Cocker Jan 1990 Nothin' To Hide Poco Jan 1990 Kickstart My Heart Motley Crue Jan 1990 I'll Be Good To You Quincy Jones f/ Ray Charles and Chaka Khan Feb 1990 Tender Lover Babyface Feb 1990 If You Leave Me Now Jaya Feb 1990 Was It Nothing At All Michael Damian Feb 1990 I Remember You Skid Row Feb 1990 Woman In Chains Tears For Fears Feb 1990 All Nite Entouch Feb 1990 Opposites Attract Paula Abdul w/ The Wild Pair Feb 1990 Walk On By Sybil Feb 1990 That's What I Like Jive Bunny & The Mastermixers Mar 1990 Summer Rain Belinda Carlisle Mar 1990 I'm Not Satisfied Fine Young Cannibals Mar 1990 Here We Are Gloria Estefan Mar 1990 Escapade Janet Jackson Mar 1990 Too Late To Say Goodbye Richard Marx Mar 1990 Dangerous Roxette Mar 1990 Sometimes She Cries Warrant Mar 1990 Price of Love Bad English Mar 1990 Dirty Deeds Joan Jett Mar 1990 Got To Have Your Love Mantronix Mar 1990 The Deeper The Love Whitesnake Mar 1990 Imagination Xymox Mar 1990 I Go To Extremes Billy Joel Mar 1990 Just A Friend Biz Markie Mar 1990 C'mon And Get My Love D-Mob Mar 1990 Anything I Want Kevin Paige Mar 1990 Black Velvet Alannah Myles Mar 1990 No Myth Michael Penn Mar 1990 Blue Sky Mine Midnight Oil Mar 1990 A Face In The Crowd Tom Petty Mar 1990 Living In Oblivion Anything Box Mar 1990 You're The Only Woman Brat Pack Mar 1990 Sacrifice Elton John Mar 1990 Fly High Michelle Enuff Z'Nuff Mar 1990 House of Broken Love Great White Mar 1990 All My Life Linda Ronstadt (f/ Aaron Neville) Mar 1990 True Blue Love Lou Gramm Mar 1990 Keep It Together Madonna Mar 1990 Hide and Seek Pajama Party Mar 1990 I Wish It Would Rain Down Phil Collins Mar 1990 Love Me For Life Stevie B.
    [Show full text]
  • Release Some Tension Swv Rar Extractor
    Release Some Tension Swv Rar Extractor Release Some Tension Swv Rar Extractor 1 / 3 2 / 3 SWV SLAMS OUT another hit cd with this r and b/rap offering, featuring collabos with some of the current hit rap artists of that time. SWV remains my favourite girl .... Release Some Tension is the third studio album by American R&B vocal group SWV. Guest appearances are made by E-40, Puff Daddy, Missy Elliott, .... rar download. Release Some Tension Swv Rar Extractor. 4/10/. Stainless Steel Tumbler - Navy Blue. SBJ My Starbucks 16oz Tumbler Template .... If you still have trouble downloading SWV - Release Some Tension (1997).rar hosted on mediafire.com 75.29 MB, or any other file, post it in comments below .... SWV Release Some Tension (1997).rar mediafire.com, file size: 75.29 MB Swv release some. ... (extract.rar files to MP3) (archives files too!). If you still have trouble downloading SWV - Release Some Tension (1997).rar hosted on mediafire.com 75.29 MB, 1978 - Some Girls.. Check out some of our functions as: BIN Checker Darkside and millions of ... Unaired. rar calculations in aas level chemistry by jim clark pdf zip The most ... to Chinese Speech and Writing Vol I SWV Release Some Tension 1997 FLA. ... ExIso GUI makes easier to extract multiple iso with a queue list and a little FTP browser.. Release Some Tension Swv Rar Extractor Average ratng: 7,6/10 5817reviews. • ' Released: February 11, 1997 • 'Someone' Released: July 30, 1997 • 'Lose My .... Free Rar And Zip Extractor. , Upload:, 14:59 225 Artist: Aleke Kanonu Title Of Album: Aleke Year Of Release: 1980 Label (Catalog#): Arcana ...
    [Show full text]
  • CONTEMPORARY RADIO's MUSIC 11 MAY 7, 1993 Conversation With
    CONTEMPORARY RADIO'S MUSIC 11 NEWS RESOURCE e ver. MAY 7, 1993 Conversation With Burt Baumgartner B-96 Spotlight Station Naked Picture On Page 6 www.americanradiohistory.com e e © THE PROCLAIMERS "I'M GONNA BE (500 MILES)" FROM THE HIT MOVIE INSTANT PHONES AT RADIO IMMEDIATE REACTION AT RETAIL!1 www.americanradiohistory.com THE Ci1&iuhs MAINSTREAM LF;ar PLAYS PER WEEK R AV6. 2W LW 1W AImsT/SOND LABEL 2W LW 11 AansT/Saec sus. PLAYSPPw 4 2 0 PM DAWN. Looking Through Patient Eyes Gee Street/Island/PLG 4 3 JO PM DAWN. Looking Through Patient Eyes 91 42.2 3842 2 1 2 VANESSA WILLIAMS and BRIAN McKNIGIR. Love Is Giant 2 1 2 VANESSA WILLIAMS and BRIAN MCKNIGHT. Love Is 90 42.5 3826 5 4 0 MICHAEL JACKSON. Who Is It Epic 26 8 Q JANET JACKSON. That's The Way Love Goes 101 34.0 3436 27 10 Q JANET JACKSON. That's The Way Love Goes Virgin 1 2 4 WHITNEY HOUSTON.I Have Nothing 86 37.0 3185 9 5 0 JOEY LAWRENCE. Nothin' My Love Can't Fix Impact/MCA 6 4 5 MICHAEL JACKSON. Who Is It 89 35.6 3165 7 6 Q BOY GEORGE. The Crying Game SBK/ERG 3 5 6 STING. If I Ever Lose My Faith In You 85 32.4 2751 10 10 JO Freak Me 11 7 0 SILK. Freak Me Keia/Elektra SILK. 66 40.2 2653 8 6 8 BOY GEORGE. Crying 12 8 Q PRINCE & THE NEW POWER GENERATION.
    [Show full text]
  • The Dick Crum Collection, Date (Inclusive): 1950-1985 Collection Number: 2007.01 Extent: 42 Boxes Repository: University of California, Los Angeles
    http://oac.cdlib.org/findaid/ark:/13030/kt2r29q890 No online items Finding Aid for the The Dick Crum Collection 1950-1985 Processed by Ethnomusicology Archive Staff. Ethnomusicology Archive UCLA 1630 Schoenberg Music Building Box 951657 Los Angeles, CA 90095-1657 Phone: (310) 825-1695 Fax: (310) 206-4738 Email: [email protected] URL: http://www.ethnomusic.ucla.edu/Archive/ ©2009 The Regents of the University of California. All rights reserved. Finding Aid for the The Dick Crum 2007.01 1 Collection 1950-1985 Descriptive Summary Title: The Dick Crum Collection, Date (inclusive): 1950-1985 Collection number: 2007.01 Extent: 42 boxes Repository: University of California, Los Angeles. Library. Ethnomusicology Archive Los Angeles, California 90095-1490 Abstract: Dick Crum (1928-2005) was a teacher, dancer, and choreographer of European folk music and dance, but his expertise was in Balkan folk culture. Over the course of his lifetime, Crum amassed thousands of European folk music records. The UCLA Ethnomusicology Archive received part of Dick Crum's personal phonograph collection in 2007. This collection consists of more than 1,300 commercially-produced phonograph recordings (LPs, 78s, 45s) primarily from Eastern Europe. Many of these albums are no longer in print, or, are difficult to purchase. More information on Dick Crum can be found in the Winter 2007 edition of the EAR (Ethnomusicology Archive Report), found here: http://www.ethnomusic.ucla.edu/archive/EARvol7no2.html#deposit. Language of Material: Collection materials in English, Croatian, Bulgarian, Serbian, Greek Access Collection is open for research. Publication Rights Some materials in these collections may be protected by the U.S.
    [Show full text]
  • The 1970 United States Computer Chess Championship: the Start of the Longest-Running Experiment in Computer Science History
    The 1970 United States Computer Chess Championship: The Start of the Longest-Running Experiment in Computer Science History Jonathan Schaeffer University of Alberta Abstract On August 31, 1970, an experiment began that continues to this day. The first chess tournament for computers was held as part of the Association for Computing Machinery’s (ACM’s) National Conference. The interest generated was tremendous, leading to ACM sponsoring an annual event until 1994. Chess competitions continue to this day, allowing for 50 years of data on the growth of artificial intelligence capabilities in this domain. During this period, program ratings have soared from roughly 1400 in 1970 to over 3500 today. The 1970 event was the first continuous competition in computer science history, and it represents the longest ongoing experiment in computer science history.1 Introduction Creating a program capable of competing with the human world chess champion was one of the first “grand challenge” problems of the fledgling research area of artificial intelligence. The importance of computer chess at the dawn of the computer age is reflected in the many computer science luminaries that contributed to the early advances in the field. This includes Claude Shannon (father of information theory), Alan Turning (creator of the Turing Machine and the Turing Test), Herbert Simon (Nobel Laureate and winner of the prestigious Turing Award), Alan Newell (Turing Award winner), and John McCarthy (Turing Award winner). In the 1950s and the 1960s, progress in developing chess programs was slow. However a breakthrough occurred with the development of MACHACK VI by Massachusetts Institute of Technology (MIT) student Richard Greenblatt.
    [Show full text]
  • Students Win MLK Scholarships by GEORGE GOLDMAN Read Their Winning Essays to More Than the Guest Speaker for the Program
    SPORTS MENU TIPS Residents get unpleasant smelling water Kid’s Corner W. 3rd Street Bridge opens to traffic As a result of malfunctioning carbon feed The West 3rd Street Bridge in the Flats Michael Fowler, who is 14 recently opened to traffic for the first time since equipment at the Garrett Morgan Water Facility re- its closure in November of 2004 for construc- Things Turn Around Cooking Up cently, some Westside, downtown and west suburban months old, is the son of Henry and Arneisha Fowler. Michael attend tion. The new $21 million bridge eliminates For Cavs With Ball Family Fun residents may be experiencing water with an unpleas- a seven mile detour and provides direct access ant taste or odor. The affected area is between the Fundale Nursery School and he to the Central Interchange and I - 490 for Flats Cuyahoga River and the Rocky River.The carbon feed likes Fruit Snacks as well as reading Area Businesses. The bridge will remain open books. Like all babies his age, he is until the weather warms, when it will be closed equipment is responsible for removing unwanted tastes, See Page 6 See Page 7 attempting to walk. again for three months for final painting of the as well as odors. For information, call (216) 664-3060. Fowler steel structure. EVOL.ASTSID 28 No. 2 Tuesday, January 16, 2007 - Friday, January 19, 2007E NEWDaily S ISSUED FRIDAY FREE FREE SERVING: LARCHMERE - WOODLAND, SHAKER SQUARE, BUCKEYE, WOODLAND, MT. PLEASANT, LEE & AVALON, HARVARD - LEE, MILES - UNION, UNIVERSITY CIRCLE AREA, READ ON - WRITE ON WARRENSVILLE HEIGHTS, VILLAGES OF NORTH RANDALL, HIGHLAND HILLS AND CITY OF EAST CLEVELAND READ ON - WRITE ON “COVERING THE NEWS TODAY FOR A BETTER TOMORROW” Students win MLK scholarships By GEORGE GOLDMAN read their winning essays to more than the guest speaker for the program.
    [Show full text]
  • The Coolest Music Book Ever Made Aka the MC 500 Vol. 1 Marcus Chapman Presents… the Coolest Music Book Ever Made Aka the MC 500 Vol
    The Coolest Music Book Ever Made aka The MC 500 Vol. 1 Marcus Chapman presents… The Coolest Music Book Ever Made aka The MC 500 Vol. 1 k Celebrating 40 Years of Sounds, Life, and Culture Through an All-Star Team of Songs Marcus Chapman For everyone who knows the joy of spending time shopping in a record store, and for the kids of the present and future who will never have that experience… Copyright © 2015 Marcus Chapman All rights reserved. ISBN: 1511780126 ISBN 13: 9781511780124 Contents Intro: What is The MC 500 and What Makes This Book So Cool? BONUS SONG: #501 Ooh . Roy Ayers 500 to 401 500 You Don’t Know How It Feels . Tom Pett y 499 Diggin’ On You. TLC 498 Here I Go Again . Whitesnake 497 Blame It . Jamie Foxx featuring T-Pain 496 Just Shopping (Not Buying Anything) . The Dramatics 495 Girls Dem Sugar . Beenie Man featuring Mya 494 My Heart Belongs To U . Jodeci 493 What’s My Name? . Rihanna featuring Drake 492 Feel the Need . Chocolate Milk 491 Midnight Flight . Jake Jacobson 490 The Big Payback . EPMD 489 Still Talkin’ . Eazy-E 488 Too Hot Ta Trot . Commodores 487 Who Dat . JT Money featuring Solé 486 Dark Vader . Instant Funk 485 Flow On (Move Me No Mountain). Above the Law 484 Fantasy . Earth, Wind & Fire 483 Payback Is a Dog . The Stylistics 452 Life Can Be Happy . Slave 482 Double Vision . Foreigner 451 I’ll Take Your Man . Salt ‘N Pepa 481 Soliloquy of Chaos . Gang Starr 480 Spirit of the Boogie .
    [Show full text]
  • Afro Queen Miss Jamaica Was Robbed of the Title, Internet Says
    Tempora Mutantur Et Nos Mutamur In Illis VOLUME 95 NUMBER 15 MIAMI, FLORIDA, NOVEMBER 29-DECEMBER 5, 2017 50 CENTS MIAMI-DADE COUNTY PUBLIC SCHOOLS School board orders audit of $1.2B bond provide an expenditure report Move comes at middle of nine-year spending plan for all GOB expenditures to By Andrea Robinson to ask questions about how Rojas’ proposal, which date by each category, school [email protected] the funds have been spent. passed by a vote of 6-3, re- board voting district, and The nine-member School quires the district to order an school name, and provide The school board has voted Board voted for two separate independent mid-point audit same to Board on a quarterly for Miami-Dade Public Schools items that call for giving a of the bond, which was ap- basis. to conduct a comprehensive closer look at how the money proved by voters in 2012. Under Gallon’s approved independent audit of the $1.2 has been spent. The direc- Gallon’s item, which passed item, administrators also billion general obligation bond tives come from the two new- unanimously, goes deeper. would have to establish a and to also publish regular est board members, Mari Tere It requires the district to put process and system to report updates about expenditures Rojas of District Six and Steve in place a mechanism for all GOB expenditures by each until all the money is spent. Gallon III of District One. The quarterly reporting of GOB category and related projects The decisions by the board items were approved at the expenditures to the school for public access.
    [Show full text]
  • 9.1 GB # Artist Title Length 01 2Pac Do for Love 04:37
    Total tracks number: 958 Total tracks length: 67:52:34 Total tracks size: 9.1 GB # Artist Title Length 01 2pac Do For Love 04:37 02 2pac Thug Mansion 03:32 03 2pac Thugz Mansion (Real) 04:06 04 2pac Wonder If Heaven Got A Ghetto 04:36 05 2pac Daz Kurupt Baby Dont Cry Remix 05:20 06 3lw No More 04:20 07 7 Mile Do Your Thing 04:49 08 8Ball & MJG You Don't Want Drama 04:32 09 112 Anywhere 04:04 10 112 Crazy over You 05:20 11 112 Cupid (Radio Mix) 04:08 12 112 Cupid 04:08 13 112 It's Over Now 04:00 14 112 Love You Like I Did 04:17 15 112 Only You (Slow Remix) 04:11 16 504 Boys Wobble Wobble Edited 03:42 17 504 Boys Wobble 03:38 18 702 Get It Together 04:50 19 702 Where My Girls At 02:45 20 1000 Clowns (Not The) Greatest Rapper 03:48 21 A Boogie Wit da Hoodie Drowning (feat. Kodak Black) 03:28 22 Aaliyah 4 Page Letter 04:50 23 Aaliyah Age Aint Nothing But A Number 03:37 24 Aaliyah Are You That Somebody 04:24 25 Aaliyah Dust Yourself Off 04:41 26 Aaliyah Hot Like Fire (Timbaland Remix 04:32 27 Aaliyah I Care 4 U 04:31 28 Aaliyah I Don't Wanna 04:12 29 Aaliyah If Your Girl Only Knew 04:50 30 Aaliyah More Than A Woman 03:48 31 Aaliyah One In A Million 04:29 32 Aaliyah Rock The Boat 04:33 33 Aaliyah The One I Gave My Heart To 03:52 34 Aaliyah Try Again 04:39 35 Aaliyah Ft.
    [Show full text]
  • Beyonce' Knowles911 - Jean F/ Mary J
    03 Bonnie & Clyde - Jay-z F/ Beyonce' Knowles911 - Jean F/ Mary J. Blige A Nightmare On My Street- Dj Jazzy Jeff #1 - Nelly ‘93 Til Infinitely - Souls Of Mischief A Perfect Evening For - Various "1, 2, 3" - Amyth 99 Red Balloons - Nena A Promise I Make - Dakota Moon 10 Commandments Of Love- Moonglows 99.9% Sure (i've Never - Mccomas A Random Act Of - South Sixty Five 10 Out Of 10 - Louchie Lou & Michie OneA 2nd Chance - C-murder A Rose In The Wind - Anggun 100% - Big Pun A 2nd Chance - C-murder A Rose Is A Rose - Edwards $100 Bill Y'all - Ice Cube A B C - Jackson 5 A Rose Is Still A Rose - Franklin, Aretha 100 Girls - Stroke 9 A Beautiful Morning - Rascals A Salty Dog - Procol Harem 100% Pure Love - Crystal Waters A Better Love - Londonbeat A Song For Mama - Boyz I I Men 100 % Pure Love - Crystal Waters A Bitter End - Dodd A Song For Mama - Boyz Ii Men 100 % Pure Love - Crystal Waters A Bitter End - Dodd A Song For My Son( Long- ? 100 % Pure Love - Crystal Waters A Boy Like You - Trick Pony A Song For The Lovers - Ashcroft 100% Pure Love - Waters A Change Would Do You - Sheryl Crow A Sorta Fairytale - Amos 1000 Oceans - Tori Amos A Child Is Born - The Ritz A Step Too Far - "john, Heather Headley & 16 Candles - Crests A Cinema In Buenos Aires,- Various A Straight Line - MichaelSherie Scott"Hutchence 17 - Cross Canadian RagweedA Conspiracy - Black Crows A String Of Pearls - Glen Miller 17 Again - Eurythmics A Country Boy Can - "chad Brock W/ Hank A Summer Song - Chad And Jeremy 17 Again - Eurythmics A.d.i.d.a.s.
    [Show full text]
  • Bell Biv Devoe, Swv & Jon B the Ultimate R&B Event! Friday, November 18
    FOR IMMEDIATE RELEASE MAY 31, 2011 RIVER ROCK CASINO RESORT PRESENTS BELL BIV DEVOE, SWV & JON B THE ULTIMATE R&B EVENT! FRIDAY, NOVEMBER 18 Richmond, BC – Bell Biv DeVoe was formed in the minds of its members, New Edition’s Ricky Bell, Michael Bivins and Ronnie DeVoe upon the departure of lead singer, Bobby Brown in 1986. But it wasn’t until 1988 that they released their first album, Poison. The album featured the title track – peaking at #1 on the Billboard R&B charts and reaching #3 on the Billboard Pop charts – along with “Do Me!”, “B.B.D. (I Thought It Was Me)?”, “When Will I See You Smile Again?” and “Dope!” The album went on to sell over three million copies and was followed by a remix album the next year. With their 1992 debut album, It’s About Time, SWV scored a string of Top Ten hits that established them as one of the most popular R&B groups of the 90’s. SWV – an acronym for Sisters with Voices – is comprised of three school friends: Coko, Taj and Lelee. Their hits include “I’m So Into You”, “Weak”, “Right Here/Human Nature”, “Always On My Mind” and “Anything”. Singer-songwriter Jon B brings a distinctive focus on smooth melodies to contemporary R&B. Proficient on keyboards, guitar, bass and drums, he’s written songs for such rap music legends as Toni Braxton, After 7 and Color Me Badd. Influenced by music found in his grandparents’ record store, he began combining 70’s soul with 90’s hip-hop on his 1995 debut album, Bonafide.
    [Show full text]