An Introduction to Astrophysics and Cosmology by Andrew Norton – 2016
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Astronomy 241: Foundations of Astrophysics I. the Solar System
Astronomy 241: Foundations of Astrophysics I. The Solar System Astronomy 241 is the first part of a year-long Prerequisites: Physics 170, Physics 272 introduction to astrophysics. It uses basic (or concurrent), and Math 242 or 252A. classical mechanics and thermodynamics to Contact: Professor Joshua Barnes analyze the structure and evolution of the ([email protected]; 956-8138) Solar System. www.ifa.hawaii.edu/~barnes/ast241 Tuesday, August 21, 2012 Astrophysics BS Degree Proposal in ASTR PHYS MATH CHEM preparation FALL 241 251A 161, 171 or 181 year 1 161L, 171L, or 181L SPRING 170 242 252A 162 year 1 170L 162L Foundations of Astrophysics I: FALL 241 272 243 253A The Solar System year 2 272L Foundations of Astrophysics II: SPRING 242 274 244 Galaxies & Stars year 2 274L Observational Astronomy & FALL 300 310 311 (or 307?) Laboratory year 3 300L 350 SPRING 301 311 Observational Project year 3 450 FALL 423 480 Stellar Astrophysics year 4 495 SPRING 496 481 Senior Project I, II year4 485 1 of: ASTR 320, 426, or 430 Tuesday, August 21, 2012 Units Text uses MKS units (meter, kilo-gram, second); e.g. G ≃ 6.674 × 10-11 m3 kg-1 s-2 (gravitational constant). Astronomers also use non-standard units: AU ≃ 1.496 × 1011 m (“average” Earth-Sun distance) 30 M⊙ ≃ 1.989 × 10 kg (Sun’s mass) yr ≃ 3.156 × 107 s (Earth’s orbital period) Tuesday, August 21, 2012 Order of Magnitude & Dimensional Analysis: An Example Given that Jupiter’s average density is slightly greater than water, estimate the orbital period of a satellite circling just above the planet. -

European Astroparticle Physics Strategy 2017-2026 Astroparticle Physics European Consortium
European Astroparticle Physics Strategy 2017-2026 Astroparticle Physics European Consortium August 2017 European Astroparticle Physics Strategy 2017-2026 www.appec.org Executive Summary Astroparticle physics is the fascinating field of research long-standing mysteries such as the true nature of Dark at the intersection of astronomy, particle physics and Matter and Dark Energy, the intricacies of neutrinos cosmology. It simultaneously addresses challenging and the occurrence (or non-occurrence) of proton questions relating to the micro-cosmos (the world decay. of elementary particles and their fundamental interactions) and the macro-cosmos (the world of The field of astroparticle physics has quickly celestial objects and their evolution) and, as a result, established itself as an extremely successful endeavour. is well-placed to advance our understanding of the Since 2001 four Nobel Prizes (2002, 2006, 2011 and Universe beyond the Standard Model of particle physics 2015) have been awarded to astroparticle physics and and the Big Bang Model of cosmology. the recent – revolutionary – first direct detections of gravitational waves is literally opening an entirely new One of its paths is targeted at a better understanding and exhilarating window onto our Universe. We look of cataclysmic events such as: supernovas – the titanic forward to an equally exciting and productive future. explosions marking the final evolutionary stage of massive stars; mergers of multi-solar-mass black-hole Many of the next generation of astroparticle physics or neutron-star binaries; and, most compelling of all, research infrastructures require substantial capital the violent birth and subsequent evolution of our infant investment and, for Europe to remain competitive Universe. -

Binocular Universe: Sly Fox September 2010 Phil Harrington
Binocular Universe is available every month on Cloudynights.com Binocular Universe: Sly Fox September 2010 Phil Harrington ast month's Stellafane convention, held atop Breezy Hill outside of Springfield, Vermont, was the best in recent memory. The skies were the Lclearest we've had in years, giving us a chance to enjoy the beauty of the summer Milky Way, which stretched from horizon to horizon. Armed with my trusty 10x50 and 16x70 binoculars, I sat back in my reclining chair and swept the plane of our Galaxy in pursuit of some old friends and new conquests. Above: Summer star map from Star Watch by Phil Harrington Binocular Universe is available every month on Cloudynights.com Above: Finder chart for this month's Binocular Universe. Chart adapted from Touring the Universe through Binoculars Atlas (TUBA), www.philharrington.net/tuba.htm Binocular Universe is available every month on Cloudynights.com Here are a few gems I bumped into along the way as I viewed the tiny constellation of Vulpecula the Fox. Vulpecula is a faint summertime constellation wedged between Cygnus (the Swan) to the north and Sagitta (the Arrow) to the south. None of Vulpecula’s stars shine brighter than magnitude 4.5, so seeing a fox here is a tall order indeed. But the sly Fox holds many binocular treasures for those who the time to seek them out. Vulpecula was created in 1687 by the Polish astronomer Johannes Hevelius. His original drawing showed a small fox carrying a hapless goose in its mouth. He called the combination Vulpecula et Anser ("the little fox and the goose"). -

A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star. -

___... -.:: GEOCITIES.Ws
__ __ _____ _____ _____ _____ ____ _ __ / / / / /_ _/ / ___/ /_ _/ / __ ) / _ \ | | / / / /__/ / / / ( ( / / / / / / / /_) / | |/ / / ___ / / / \ \ / / / / / / / _ _/ | _/ / / / / __/ / ____) ) / / / /_/ / / / \ \ / / /_/ /_/ /____/ /_____/ /_/ (_____/ /_/ /_/ /_/ _____ _____ _____ __ __ _____ / __ ) / ___/ /_ _/ / / / / / ___/ / / / / / /__ / / / /__/ / / /__ / / / / / ___/ / / / ___ / / ___/ / /_/ / / / / / / / / / / /___ (_____/ /_/ /_/ /_/ /_/ /_____/ _____ __ __ _____ __ __ ____ _____ / ___/ / / / / /_ _/ / / / / / _ \ / ___/ / /__ / / / / / / / / / / / /_) / / /__ / ___/ / / / / / / / / / / / _ _/ / ___/ / / / /_/ / / / / /_/ / / / \ \ / /___ /_/ (_____/ /_/ (_____/ /_/ /_/ /_____/ A TIMELINE OF THE MULTIVERSE Version 1.21 By K. Bradley Washburn "The Historian" ______________ | __ | | \| /\ / | | |/_/ / | | |\ \/\ / | | |_\/ \/ | |______________| K. Bradley Washburn HISTORY OF THE FUTURE Page 2 of 2 FOREWARD Relevant Notes WARNING: THIS FILE IS HAZARDOUS TO YOUR PRINTER'S INK SUPPLY!!! [*Story(Time Before:Time Transpired:Time After)] KEY TO ABBREVIATIONS AS--The Amazing Stories AST--Animated Star Trek B5--Babylon 5 BT--The Best of Trek DS9--Deep Space Nine EL--Enterprise Logs ENT--Enterprise LD--The Lives of Dax NE--New Earth NF--New Frontier RPG--Role-Playing Games S.C.E.--Starfleet Corps of Engineers SA--Starfleet Academy SNW--Strange New Worlds sQ--seaQuest ST--Star Trek TNG--The Next Generation TNV--The New Voyages V--Voyager WLB—Gateways: What Lay Beyond Blue italics - Completely canonical. Animated and live-action movies, episodes, and their novelizations. Green italics - Officially canonical. Novels, comics, and graphic novels. Red italics – Marginally canonical. Role-playing material, source books, internet sources. For more notes, see the AFTERWORD K. Bradley Washburn HISTORY OF THE FUTURE Page 3 of 3 TIMELINE circa 13.5 billion years ago * The Big Bang. -

Cvetoje- Vic, Anthony Cheetham, Frantz Martinache, Barnaby Norris, Peter Tuthill
Dr Benjamin Pope Lecturer in Astrophysics and DECRA Fellow Advisor: Prof. David Hogg Affiliation: School of Mathematics & Physics University of Queensland, St Lucia, QLD 4072, Australia and Centre for Astrophysics University of Southern Queensland, West Street, Toowoomba, QLD 4350, Australia Homepage: benjaminpope.github.io email: [email protected] orcid: 0000-0003-2595-9114 Education and Previous Positions 2017-2020 NASA Sagan Fellow, New York University Advisor: Prof. David Hogg 2017 Postdoctoral Research Associate, University of Sydney Advisor: Prof. Peter Tuthill 2013-2017 Doctor of Philosophy in Astrophysics, University of Oxford Thesis: “Observing Bright Stars and their Planets from the Earth and from Space” Balliol College | Supervisors: Prof. Suzanne Aigrain, Prof. Patrick Roche 2013-14 Master of Science in Astrophysics, University of Sydney Thesis: “Vision and Revision: Wavefront Sensing from the Image Domain” Supervisor: Prof. Peter Tuthill 2012 Bachelor of Science (Advanced) with Honours in Physics, University of Sydney First Class Honours, with the University Medal Thesis: “Dancing in the Dark: Kernel Phase Interferometry of Ultracool Dwarfs” Supervisors: Prof. Peter Tuthill, Dr. Frantz Martinache 2010-2011 Study Abroad at the University of California, Berkeley Research project with Prof. Charles H. Townes, Infrared Spatial Interferometer. Grants ARC Discovery Early Career Research Award (DECRA) AUD $444,075.00 NASA TESS Cycle 3 Guest Investigator USD $50,000 TESS Cycle 2 Guest Investigator USD $50,000 Balliol Balliol Interdisciplinary Institute Research Grant College GBP £3,000 Teaching 2021 Extragalactic Astrophysics & Cosmology, University of Queensland 2019 Master of Data Science Guest Lecturer, NYU Center for Data Science 2017 Bayesian Reasoning Honours Lecturer, University of Sydney 2017 Honours Project Supervisor, University of Sydney Supervised Alison Wong and Matthew Edwards, both to First Class Honours and PhD acceptance. -

Appendix A: Scientific Notation
Appendix A: Scientific Notation Since in astronomy we often have to deal with large numbers, writing a lot of zeros is not only cumbersome, but also inefficient and difficult to count. Scientists use the system of scientific notation, where the number of zeros is short handed to a superscript. For example, 10 has one zero and is written as 101 in scientific notation. Similarly, 100 is 102, 100 is 103. So we have: 103 equals a thousand, 106 equals a million, 109 is called a billion (U.S. usage), and 1012 a trillion. Now the U.S. federal government budget is in the trillions of dollars, ordinary people really cannot grasp the magnitude of the number. In the metric system, the prefix kilo- stands for 1,000, e.g., a kilogram. For a million, the prefix mega- is used, e.g. megaton (1,000,000 or 106 ton). A billion hertz (a unit of frequency) is gigahertz, although I have not heard of the use of a giga-meter. More rarely still is the use of tera (1012). For small numbers, the practice is similar. 0.1 is 10À1, 0.01 is 10À2, and 0.001 is 10À3. The prefix of milli- refers to 10À3, e.g. as in millimeter, whereas a micro- second is 10À6 ¼ 0.000001 s. It is now trendy to talk about nano-technology, which refers to solid-state device with sizes on the scale of 10À9 m, or about 10 times the size of an atom. With this kind of shorthand convenience, one can really go overboard. -

Astrometry and Optics During the Past 2000 Years
1 Astrometry and optics during the past 2000 years Erik Høg Niels Bohr Institute, Copenhagen, Denmark 2011.05.03: Collection of reports from November 2008 ABSTRACT: The satellite missions Hipparcos and Gaia by the European Space Agency will together bring a decrease of astrometric errors by a factor 10000, four orders of magnitude, more than was achieved during the preceding 500 years. This modern development of astrometry was at first obtained by photoelectric astrometry. An experiment with this technique in 1925 led to the Hipparcos satellite mission in the years 1989-93 as described in the following reports Nos. 1 and 10. The report No. 11 is about the subsequent period of space astrometry with CCDs in a scanning satellite. This period began in 1992 with my proposal of a mission called Roemer, which led to the Gaia mission due for launch in 2013. My contributions to the history of astrometry and optics are based on 50 years of work in the field of astrometry but the reports cover spans of time within the past 2000 years, e.g., 400 years of astrometry, 650 years of optics, and the “miraculous” approval of the Hipparcos satellite mission during a few months of 1980. 2011.05.03: Collection of reports from November 2008. The following contains overview with summary and link to the reports Nos. 1-9 from 2008 and Nos. 10-13 from 2011. The reports are collected in two big file, see details on p.8. CONTENTS of Nos. 1-9 from 2008 No. Title Overview with links to all reports 2 1 Bengt Strömgren and modern astrometry: 5 Development of photoelectric astrometry including the Hipparcos mission 1A Bengt Strömgren and modern astrometry .. -
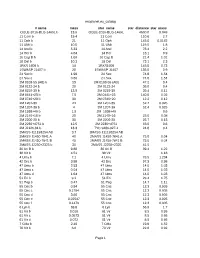
Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55 -

A Review on Substellar Objects Below the Deuterium Burning Mass Limit: Planets, Brown Dwarfs Or What?
geosciences Review A Review on Substellar Objects below the Deuterium Burning Mass Limit: Planets, Brown Dwarfs or What? José A. Caballero Centro de Astrobiología (CSIC-INTA), ESAC, Camino Bajo del Castillo s/n, E-28692 Villanueva de la Cañada, Madrid, Spain; [email protected] Received: 23 August 2018; Accepted: 10 September 2018; Published: 28 September 2018 Abstract: “Free-floating, non-deuterium-burning, substellar objects” are isolated bodies of a few Jupiter masses found in very young open clusters and associations, nearby young moving groups, and in the immediate vicinity of the Sun. They are neither brown dwarfs nor planets. In this paper, their nomenclature, history of discovery, sites of detection, formation mechanisms, and future directions of research are reviewed. Most free-floating, non-deuterium-burning, substellar objects share the same formation mechanism as low-mass stars and brown dwarfs, but there are still a few caveats, such as the value of the opacity mass limit, the minimum mass at which an isolated body can form via turbulent fragmentation from a cloud. The least massive free-floating substellar objects found to date have masses of about 0.004 Msol, but current and future surveys should aim at breaking this record. For that, we may need LSST, Euclid and WFIRST. Keywords: planetary systems; stars: brown dwarfs; stars: low mass; galaxy: solar neighborhood; galaxy: open clusters and associations 1. Introduction I can’t answer why (I’m not a gangstar) But I can tell you how (I’m not a flam star) We were born upside-down (I’m a star’s star) Born the wrong way ’round (I’m not a white star) I’m a blackstar, I’m not a gangstar I’m a blackstar, I’m a blackstar I’m not a pornstar, I’m not a wandering star I’m a blackstar, I’m a blackstar Blackstar, F (2016), David Bowie The tenth star of George van Biesbroeck’s catalogue of high, common, proper motion companions, vB 10, was from the end of the Second World War to the early 1980s, and had an entry on the least massive star known [1–3]. -

Binocular Double Star Logbook
Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club. -

Institute of Astronomy Postgraduate Student Handbook 2015–2016
Institute of Astronomy Postgraduate Student Handbook 2015–2016 Contents 1 Welcome 1 2 New Arrivals 2 3 Potential Supervisors and their Research Interests4 4 Departmental Life 19 5 Outreach Activities 28 6 Computers 30 7 Reference 36 8 Who’s Who 40 9 Evaluation 44 10 Travel and Money Issues (for PhD students) 48 11 Undergraduate Teaching 51 12 Other Resources 54 13 Researcher Development 58 14 Survival Tips for Living and Working in Cambridge 62 15 Life outside the IoA and Astronomy 68 16 Some Fellow Students 77 17 Credits 88 This document is available in PDF format at http://www.ast.cam.ac.uk/sites/default/files/postgrad_handbook.pdf 3 1 Welcome Andy Fabian As the Director of the Institute of Astronomy, it gives me great pleasure to welcome you at the start of your graduate studies in astrophysics. The Institute is one of the leading centres of astrophysical research in the world and the staff, together with the almost constant stream of visitors, provides a fantastic scientific environment in which to work. Formal and informal occasions to foster commu- nication and acquire a breadth of knowledge in astrophysics (morning coffee and afternoon tea, the seminar and colloquia series) are a key part of the Institute. Reaching outwards, the active Outreach programme, in which graduate students play a major role, connects us to the public (from eight to 80 years of age). For many new Ph.D. students, even those with “astrophysics” degrees, the options for acquiring familiarity with the extensive range of research topics and type that exist within the subject have been limited.