DOCSLIB.ORG

A Study of Hadronic Punchthrough at the RD5 Experimental Setup VERBUM

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Study of Hadronic Punchthrough at the RD5 Experimental Setup VERBUM A Study of Hadronic Punchthrough at the RD5 Experimental Setup VERBUM Lithograph, July 1942, 33.2 38.6 cm M.C. Escher's ªVerbumº c 1997 Cordon Art ± Baarn ± Holland. All rights reserved. A Study of Hadronic Punchthrough at the RD5 Experimental Setup Een wetenschappelijke proeve op het gebied van de Natuurwetenschappen. Proefschrift ter verkrijging van de graad van doctor aan de Katholieke Universiteit Nijmegen, volgens besluit van het College van Decanen in het openbaar te verdedigen op donderdag 10 april 1997, des namiddags om 3.30 uur precies, door Robert Bergman geboren op 1 april 1964 te Zwolle. Promotor: Prof. Dr. E.W. Kittel Co-promotor: Dr. A.C. KonigÈ Manuscriptcommissie: Dr. Ir. H. van der Graaf Dr. Ir. C.L.A. Pols ISBN: 90-9010437-2 Ter nagedachtenis aan Henk .... and eventually human beings arrived. The human beings were different primarily because they were the only species intensely curious about their surroundings. In time, mutations occured, and an odd subset of humans began roaming the land. They were arrogant. They were not content to enjoy the magni®cence of the universe. They asked "How?". How was the universe created? How can the "stuff" of the universe be responsible for the incredible variety in our world: stars, planets, sea otters, oceans, coral, sunlight, the human brain? The mutants had posed a question that could be answered - but only with the labor of millennia and with a dedication handed down from the master to student for a hundred of generations. The question also inspired a great number of wrong and embarrassing answers. Fortunately, these mutants were born without a sense of embarrassment. The were called physicists. ± Leon Lederman with Dick Teresi in 'The God Particle' [1] Contents 1 Elementary Particles 1 1.1 Introduction 1 1.2 Standard Model 2 1.2.1 Electroweak Interactions 3 1.2.2 Strong Interactions 4 1.2.3 Higgs Mechanism 5 1.3 Experimental Status 5 2 Large Hadron Collider 7 2.1 Experimental Particle Physics 7 2.2 LHC: Proton-Proton Collider 8 2.3 Detectors for LHC 9 2.3.1 ATLAS 11 2.3.1.1 Inner Detector in Solenoidal Magnetic Field 11 2.3.1.2 Calorimeter 12 2.3.1.3 Muon Detector in Toroidal Magnetic Field 12 2.3.1.4 Muon Spectrometer Performance 15 2.3.2 CMS 16 2.4 Physics at the LHC 17 2.4.1 Standard Model Higgs Boson 17 2.4.1.1 Higgs Boson Production 19 2.4.1.2 Higgs Boson Decays and Experimental Signatures 20 2.4.1.3 Four-Muon Decay Mode and its Backgrounds 22 2.4.2 Quark, Neutrino and Beyond SM Physics 25 3 Honeycomb Strip Chamber 27 3.1 Introduction 27 3.2 Charged Particle Detection 27 3.2.1 Energy Loss of Charged Particles 27 3.2.2 Energetic Knock-On Electrons 29 3.3 Motion of Charges in Gases 30 3.3.1 Electron and Ion Diffusion 30 3.3.2 Electron and Ion Drift 31 3.3.3 Drift in a Magnetic Field 32 3.3.4 Electron Attachment 34 i ii Contents 3.4 Ampli®cation of Ionization 35 3.4.1 The Proportional Mode and Beyond 35 3.4.2 Ampli®cation Factor in the Proportional Mode 38 3.4.3 The Signal Development 40 3.4.3.1 Signal Generation on the Anode 40 3.4.3.2 Signal Generation on the Cathode 41 3.5 Honeycomb Strip Chamber 41 3.5.1 Principle and Construction 41 3.5.2 Drift Time Measurement with the Anode Wire 42 3.5.3 Charge Ratio Measurement with the Cathode Strips 43 4 Tracking Calorimeter 45 4.1 Introduction 45 4.2 Sampling Calorimetry 46 4.3 Electromagnetic Showers 47 4.3.1 Interaction Processes 47 4.3.2 Shape of the Particle Shower 51 4.3.3 Energy Resolution 52 4.3.4 Sampling Calorimeter Response 53 4.4 Hadronic Showers 54 4.4.1 General Attributes 54 4.4.2 Dimensions of the Particle Shower 55 4.4.3 Calorimeter Performance 56 4.4.3.1 The eh Signal Ratio 56 4.4.3.2 Calorimeter Response 57 4.4.3.3 Compensating Hadron Calorimeter 58 4.4.3.4 Achieving Compensation 60 4.4.4 Energy Resolution 61 4.5 Tracking Calorimeter 62 4.5.1 Goals of the Tracking Calorimeter 62 4.5.2 Mechanical Construction of the HSC layers 64 4.5.2.1 Folding and Assembly of the Foil 65 4.5.2.2 Assembly and Wiring of a Single-Layer HSC 66 4.5.3 Assembly of the Calorimeter 68 4.5.4 TRACAL Readout Electronics 68 4.5.4.1 Wire Signals 68 4.5.4.2 Strip Signals 69 4.5.4.3 Calibration 70 5 Experimental Setup of RD5 73 5.1 Introduction 73 5.2 Beam Line for RD5 74 5.3 Description of the RD5 Detector 77 5.3.1 Magnets 79 5.3.2 Trigger 80 Contents iii 5.3.3 Beam De®nition 81 5.3.4 Tracking Calorimeter 82 5.3.4.1 Drift Time Measurement in TRACAL 82 5.3.4.2 Identi®cation of Electromagnetic Secondaries 85 5.3.5 Resistive Plate Chambers 88 5.3.6 Muon Drift Chambers 89 5.3.7 Data Acquisition System 90 6 Punchthrough Measurements 91 6.1 Introduction 91 6.2 Total Punchthrough Probability 91 6.2.1 Punchthrough Data Sample 91 6.2.2 Determination of Punchthrough Probability 93 6.2.2.1 Penetration Depth 93 6.2.2.2 Muon Background Subtraction 97 6.2.3 Description of RD5 Punchthrough Simulation 105 6.2.4 Results for Hadron-Induced Showers 106 6.2.4.1 Total Punchthrough Probability 106 6.2.4.2 Shower Lateral Distribution in TRACAL 112 6.2.4.3 Shower Multiplicity Distribution in TRACAL 113 6.3 Momentum and Angular Distribution of Punchthrough Muons 114 6.3.1 Determination of Punchthrough Muon Momentum 114 6.3.1.1 Momentum Fit of Punchthrough Muons 115 6.3.1.2 Description of Simulation 115 6.3.2 Momentum Distribution of Punchthrough Muons 116 6.3.3 Angular Distribution of Punchthrough Muons 120 6.4 Summary and Conclusions 122 A Physical Constants 123 B Acronyms 125 C Punchthrough Tables 127 Bibliography 133 Summary 141 Samenvatting 143 Dankwoord 147 Curriculum Vitae 149 1 Elementary Particles Nothing exists except 'atomos' and empty space; everything else is opinion. th ± Democritus ( century B.C.) 1.1 Introduction Elementary particle physics or high energy physics attempts to describe nature at a fundamental level. The objects of investigations are the ultimate constituents of matter, their interactions and the particles which mediate these interactions. For millenia mankind has tried to understand nature. A number of concepts still in use today were already introduced by the ancient Greek philosophers. For instance, the notion that matter consists of indivisible building blocks (atoms) was ®rst introduced by Democritus around B.C. About the same time Empedocles launched his vision that all materials were composed of only four ªelementsº: earth, water, air and ®re. Obviously the meaning and interpretation of these concepts has changed since the epoch of th the ancient philosophers. The atom was revitalised by the work of Dalton in the century. The role of the original four elements was replaced by almost a hundred chemical elements, culminating in the construction of the periodic table of the elements by Mendeleev in . The empty places in the periodic table belonged to elements still to be discovered. Based on their expected chemical properties some elements were indeed observed within a few years and proved the periodic table to be successful. Furthermore, the regularity of the periodic table suggested an underlying structure. It took the discovery of both the electron [2] and the atomic nucleus [3], together with the development of quantum mechanics to explain this structure. After the discovery of the neutron [4±6] also the composition of the nucleus became evident. The elementary particles needed to form the atoms of the chemical
Load more

Recommended publications
  • The LHC Project and Future of CERN
    The LHC Project and Future of CERN Robert Aymar Symposium on Physics of Elementary Interactions in the LHC Era Warsaw, 21–22 April 2008 Contents about CERN: a facility for the benefit of the European Particle Physics Community the LHC project: completion of installation, start of commissioning for accelerator, experiments and computing, the CNGS: start of operations and the CLIC scheme for multi Tev e+e- Linear Collider plans for CERN in the next decade Warsaw, 21-22 April 2008 2 CERN… • Seeking answers to questions about the Universe • Advancing the frontiers of technology • Training the scientists of tomorrow • Bringing nations together through science 33 CERN in Numbers • 2415 staff* • 730 Fellows and Associates* • 9133 users* • Budget (2007) 982 MCHF (610M Euro) *5 February 2008 • Member States: Austria, Belgium, Bulgaria, the Czech Republic, Denmark, Finland, France, Germany, Greece, Hungary, Italy, Netherlands, Norway, Poland, Portugal, Slovakia, Spain, Sweden, Switzerland and the United Kingdom. • Observers to Council: India, Israel, Japan, the Russian Federation, the United States of America, Turkey, the European Warsaw, 21-22Commission April 2008 and Unesco 4 Distribution of All CERN Users by Nation of Institute on 5 February 2008 Warsaw, 21-22 April 2008 5 CERN: the World’s Most Complete Accelerator Complex (not to scale) Warsaw, 21-22 April 2008 6 TheThe LongLong--TermTerm ScientificScientific ProgrammeProgramme Legend: Approved Under Consideration 2007 2008 2009 2010 2011 LHC Experiments ALICE ATLAS CMS LHCb TOTEM LHCf Other LHC Experiments (e.g. MOEDAL) Non-LHC Experimental Programme SPS NA58 (COMPASS) P326 (NA48/3)/NA62 P327 (EM processes in strong crystalline fields) NA49-future/NA61 Neutrino / CNGS New initiatives PS PS212 (DIRAC) PS215 (CLOUD) OTHER FACILITIES AD ISOLDE n-TOF Neutron CAST P331 (optical axion search and QED test) Test Beams North Areas West Areas East Hall R&D (Detector & Accelerator) 7 Poland and the Four Strategic Missions of CERN FUNADAMENTAL RESEARCH • Polish physicists collaborate with CERN since 1959.
    [Show full text]
  • HERA Collisions CERN LHC Magnets
    The Gallex (gallium-based) solar neutrino experiment in the Gran Sasso underground Laboratory in Italy has seen evidence for neutrinos from the proton-proton fusion reaction deep inside the sun. A detailed report will be published in our next edition. again, with particles taken to 26.5 aperture models are also foreseen to GeV and initial evidence for electron- CERN test coil and collar assemblies and a proton collisions being seen. new conductor distribution will further Earlier this year, the big Zeus and LHC magnets improve multipole components. H1 detectors were moved into A number of other models and position to intercept the first HERA With test magnets for CERN's LHC prototypes are being built elsewhere collisions, and initial results from this proton-proton collider regularly including a twin-aperture model at new physics frontier are eagerly attaining field strengths which show the Japanese KEK Laboratory and awaited. that 10 Tesla is not forbidden terri­ another in the Netherlands (FOM-UT- tory, attention turns to why and NIHKEF). The latter will use niobium- where quenches happen. If 'training' tin conductor, reaching for an even can be reduced, superconducting higher field of 11.5 T. At KEK, a magnets become easier to commis­ single aperture configuration was sion. Tests have shown that successfully tested at 4.3 K, reaching quenches occur mainly at the ends of the short sample limit of the cable the LHC magnets. This should be (8 T) in three quenches. This magnet rectifiable, and models incorporating was then shipped to CERN for HERA collisions improvements will soon be reassem­ testing at the superfluid helium bled by the industrial suppliers.
    [Show full text]
  • Trigger and Data Acquisition
    Trigger and data acquisition N. Ellis CERN, Geneva, Switzerland Abstract The lectures address some of the issues of triggering and data acquisition in large high-energy physics experiments. Emphasis is placed on hadron-collider experiments that present a particularly challenging environment for event se- lection and data collection. However, the lectures also explain how T/DAQ systems have evolved over the years to meet new challenges. Some examples are given from early experience with LHC T/DAQ systems during the 2008 single-beam operations. 1 Introduction These lectures concentrate on experiments at high-energy particle colliders, especially the general- purpose experiments at the Large Hadron Collider (LHC) [1]. These experiments represent a very chal- lenging case that illustrates well the problems that have to be addressed in state-of-the-art high-energy physics (HEP) trigger and data-acquisition (T/DAQ) systems. This is also the area in which the author is working (on the trigger for the ATLAS experiment at LHC) and so is the example that he knows best. However, the lectures start with a more general discussion, building up to some examples from LEP [2] that had complementary challenges to those of the LHC. The LEP examples are a good reference point to see how HEP T/DAQ systems have evolved in the last few years. Students at this school come from various backgrounds — phenomenology, experimental data analysis in running experiments, and preparing for future experiments (including working on T/DAQ systems in some cases). These lectures try to strike a balance between making the presentation accessi- ble to all, and going into some details for those already familiar with T/DAQ systems.
    [Show full text]
  • India-CMS Newsletter Member Institutes/ Universities of India-CMS
    India-CMS Newsletter Member Institutes/ Universities of India-CMS Vol 1. No. 1, July 2015 1. Nuclear Physics Division (NPD) Bhabha Atomic Research Center (BARC) Mumbai http://www.barc.gov.in/ First volume produced at: 2. Indian Institute of Science Education and Research (IISER) Department of Physics Pune http://www.iiserpune.ac.in Panjab University Sector 14 Chandigarh - 160014 3. Indian Institute of Technology (IIT), Bhubaneswar Bhubaneswar http:// www.iitbbs.ac.in 4. Department of Physics Indian Institute of Technology (IIT), Bombay Mumbai http://www.iitb.ac.in/en/education/academic-divisions 5. Indian Institute of Technology (IIT), Madras Chennai https://www.iitm.ac.in 6. School of Physical Sciences National Institute of Science Education and Research (NISER), Edited and Compiled by: Bhubaneswar http://physics.niser.ac.in/ Manjit Kaur Department of Physics 7. Department of Physics Panjab University Panjab University Chandigarh Chandigarh http://physics.puchd.ac.in/ [email protected] 8. Division of High Energy Nuclear and Particle Physics Ajit Mohanty Saha Institute of Nuclear Physics (SINP) Director Kolkata http://www.saha.ac.in/web/henppd-home Saha Institute of Nuclear Physics (SINP) Kolkatta 9. Department of High Energy Physics [email protected] Tata Institute of Fundamental Research (TIFR), Mumbai http://www.tifr.res.in/ ~dhep/ Abhimanyu Chawla Department of Physics 10. Department of Physics & Astrophysics Panjab University University of Delhi Chandigarh Delhi http://www.du.ac.in/du/index.php?page=physics-astrophysics [email protected] 11. Visva Bharti Santiniketan, West Bengal 731204 http://www.visvabharati.ac.in/Address.html 1 2 Contents Message ........................................................................................................................................................ 3 Message .......................................................................................................................................................
    [Show full text]
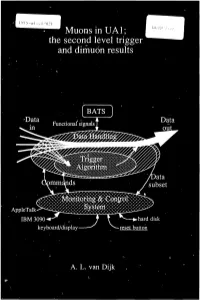
  • The Second Level Trigger and Dimuon Results
    ••~ Muonsin UA1; the second level trigger and dimuon results BATS -Data Functional signals /Data )mm; subset AppleTalk. S\S\ IBM 3090 •hard disk keyboard/display • reset button A. L. van Dijk Muons inUAl; the second level trigger and dimuon results ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit van Amsterdam, op gezag van de Rector Magnificus Prof. Dr. P. W. M. de Meijer, in het openbaar te verdedigen in de Aula der Universiteit (Oude Lutherse Kerk, ingang Singel 411, hoek Spui) op dinsdag 26 februari 1991 te 15:00 uur. door Adriaan Louis van Dijk geboren te Amsterdam Promotor: Prof. Dr. J. J. Engelen Co-Promotor: Dr. K. Bos The work described in this thesis is part of the research program of the 'Nationaal Instituut voor Kernfysica en Hoge Energie Fysica (NIKHEFH)'. The author was financially supported by the 'Stichting voor Fundamenteel Onderzoek der Materie (FOM)'. Contents I Introduction 1 1.1 Proton-ontlproton physics, motivation 1 1.2 The CERN proton-antiprolon collider 2 1.3 Collider performance and physics achievements 3 1.4 Jets, muons, heavy flavours and flavour mixing S 1.5 Outline of this thesis 7 II TheUAl Experiment 8 2.1 Introduction 8 2.2 The UA1 coordinate system 10 2.3 Central detector (CD) 11 2.4 The Hadronic Calorimeter 14 2.5 Muon detection system IS 2.6 Triggering and daia acquisition (1987-1990) 18 III Data Acquisition and Triggers 20 3.1 Introduction 20 3.2 Daia acquisition 21 3.2.2 The Event Building 23 3.2.3 Hardware and standards 23 3.2.4 Software 24 3.2.5 Ergonomics 24 3.3
    [Show full text]
  • Antiprotons in the Big Machine
    Antiprotons in the big machine Right the beam line which injects 26 GeV antiprotons into the SPS. Centre, the beam fine which sends high energy protons from the SPS towards the West Experimental Area. The main ring is on the left. (Photo CERN 38.4.81) On 7 July a pulse of antiprotons was sent to the CERN Super Proton Synchrotron, accelerated to 270 GeV and (briefly) stored. Two days later the exercise was repeated with greater success and the first evi­ dence obtained for proton-antipro­ ton collisions at 540 GeV — by far the highest collision energies ever achieved. Although there is still much to be done before the scheme becomes fully operational, this achievement is a major milestone in the CERN antiproton story. The origins of the project Antiprotons, since they presuma­ bly have the same properties as protons except for the sign of their electric charge, can be accelerated and stored in the same magnet ring as protons. Thus colliding beam sys­ tems, like the familiar electron-posi­ tron machines, are, in principle, fea­ sible. However until recently it was not possible to produce antiproton tion, the antiprotons emerge with a for colliding beam physics. It in­ beams of sufficient intensity and wide range of momenta, distinctly volves using electron beams travel­ density to give sufficient collisions in unsuitable for a magnet system in a ling along with the antiproton beam a reasonable enough time for useful beam transfer line, an accelerator or at the same velocity. The electron physics to be done. a storage ring which is designed to beam, which is much easier to con­ This situation has changed with handle a well defined particle mo­ trol, has particles at precisely the the invention of 'beam cooling'.
    [Show full text]
  • QCD Studies at L3
    QCD Studies at L3 Swagato Banerjee Tata Institute of Fundamental Research Mumbai 400 005 2002 QCD Studies at L3 Swagato Banerjee Tata Institute of Fundamental Research Mumbai 400 005 A Thesis submitted to the University of Mumbai for the degree of Doctor of Philosophy in Physics March, 2002 To my parents Acknowledgement It has been an extremely enlightening and enriching experience working with Sunanda Banerjee, supervisor of this thesis. I would like to thank him for his forbearance and encouragement and for teaching me the different aspects of the subject with lots of patience. I thank all the members of the Department of High Energy Physics of Tata Institute of Fundamental Research (TIFR) for providing various facilities and support, and ideal ambiance for research. In particular, I would like to thank B.S. Acharya, T. Aziz, Sudeshna Banerjee, B.M. Bellara, P.V. Deshpande, S.T. Divekar, S.N. Ganguli, A. Gurtu, M.R. Krishnaswamy, K. Mazumdar, M. Maity, N.K. Mondal, V.S. Narasimham, P.M. Pathare, K. Sudhakar and S.C. Tonwar. Asesh Dutta, Dilip Ghosh, S. Gupta, Krishnendu Mukherjee, Sreerup Ray Chaudhuri, D.P. Roy, Sourov Roy, Gavin Salam and K. Sridhar provided valuable theoretical insight on various occasions. My heartfelt thanks to them. I thank the European Organisation for Nuclear Research (CERN) for its kind hospitality and all the members of the Large Electron Positron (LEP) accelerator group for successful operation over the last decade. The members of the L3 collaboration and the LEP QCD Working Group provided me a stim- ulating working environment. In particular, I thank Pedro Abreu, Satyaki Bhattacharya, Gerard Bobbink, Ingrid Clare, Robert Clare, Glen Cowan, Aaron Dominguez, Dominique Duchesneau, John Field, Ian Fisk, Roger Jones, Mehnaz Hafeez, Stephan Kluth, Wolfgang Lohmann, Wes- ley Metzger, Peter Molnar, Oliver Passon, Martin Pohl, Subir Sarkar, Chris Tully and Micheal Unger.
    [Show full text]
  • The a to Z of Accelerators
    present explanation for this behav­ The long timescale needed to terparts. But superconductivity iour is that superconductivity exists produce acceptable conductors of above 77K provides a powerful in many discrete regions within niobium-tin (10-12 years) following stimulant to solve the technological the sample but only weak coupling its discovery in 1962 inevitably problems of dealing with brittle exists between these regions. This comes to mind in assessing the materials. The next few months weak coupling is strongly dimin­ potential timeîscales for developing could give us many more surprises ished by an external field. Electro­ high field magnets with the new in an area where none were sus­ magnetic and structural character­ materials. These new oxides, like pected only a few months ago. izations of these compounds are niobium-tin and the other A15 The discovery of Bednorz and proceeding furiously and we may compounds are inherently brittle Muller has given a profound new soon expect to know whether this and this is bound to affect their stimulus to superconductivity and percolative nature of the supercon­ application in magnets, just as the last discovery has surely not ductivity is inherent in the material large scale construction of niobium- yet been made. or results from the way present tin magnets has lagged behind samples are being prepared. their ductile niobium-titanium coun­ The A to Z of accelerators With great skill, the organizers physics but this information was 1965. The attendance of over of the 1987 Particle Accelerator surpassed in volume by reports 1100 was another reflection of Conference arranged a vast pro­ from the many other areas where the wealth of activity in the field.
    [Show full text]
  • Powermod™1 the Power You Need Sm
    INTERNATIONAL JOURNAL OF HIGH-ENERGY PHYSICS 1 PowerMod™ The Power You Need sm High Voltage.Solid-State Modulators At Diversified Technologies, we manufacture leading-edge solid state, high power modulators from our patented, modular design. PowerMod™ systems can meet your pulsed power needs - at up to 200 kV, with peak currents up to 2000 A. V PowerMod*™ HVPM 100-300 30 MWModulator (36" x 48" x 60") PowerMod™ HVPM 20-150 Pulse: 20 kV, 100A, ljis/div PowerMod™ Modulators deliver the superior benefits of solid state technology including: • Very high operating efficiencies • < 3V/kV voltage drop accross the switch PowerMod™ HVPM 20-300 6 MW Modulator (19" x 30" x 24") • <1mA leakage • Arbitrary pusewidths from less than 1 jus to DC • PRFsto30kHz • Opening and closing operation Call us or visit our website today to learn more about the PowerMod™ line of solid-state high power systems. DIVERSIFIED TECHNOLOGIES, INC. 35 Wiggins Avenue Bedford, MA 01730 781-275-9444 www. d i vt ecs.com PowerMod*™ HVPM 2.5-150 3 75 KW Modulator (19" x 19.5" x 8.5") D 1999 Diversified Technologies, Inc. PowerMod™ is a trademark of Diversified Technologies, Inc. Contents Covering current developments in high- energy physics and related fields worldwide CERN Courier is distributed to Member State governments, institutes and laboratories affiliated with CERN, and to their personnel. It is published monthly except January and August, in English and French editions. The views expressed are not necessar­ ily those of the CERN management. CERN Editor: Gordon Fraser CERN,
    [Show full text]
  • Baryon Production in Z Decay
    Baryon Pro duction in Z Decay Christopher G Tully A DISSERTATION PRESENTED TO THE FACULTY OF PRINCETON UNIVERSITY IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY RECOMMENDED FOR ACCEPTANCE BY THE DEPARTMENT OF PHYSICS January ABSTRACT How quarks b ecome conned into ordinary matter is a dicult theoretical question The p ointatwhich this o ccurs cannot b e measured by exp eriment but other prop erties related to connement can Baryon pro duction is a situation where one typ e of connement is chosen over another In this thesis pro duction rate measurements have b een p erformed for and baryons pro duced in hadronic decays of the Z The rates are low compared to meson pro duction but the particular prop erties of and decay allow these particles to be identied amongst the many mesons accompanying them The average number of and per hadronic Z decay was found to be D E N stat syst and D E N stat syst resp ectively These measurements take advantage of the unique photon detection capa bility of the L Exp eriment The rates are in agreement with those measured by other LEP detectors iii CONTENTS Abstract iii Acknowledgements v Intro duction Particle Creation and Detection Searching for Particle Decays Going Back in Time The History Behind SubNuclear Particles Quarks Discovery of the Pion The Quark Constituent Mo del
    [Show full text]
  • Around the Laboratories
    Around the Laboratories CERN Antiprotons 1985 Although the new Fermilab Teva- tron took the world collision energy record, 1985 was still a vintage year for CERN antiprotons. The scene was set last March /hen the ambitious attempt to ramp protons and antiprotons up and down between 100 and 450 GeV in the SPS was imme­ diately successful, providing the first glimpse of physics at collision energies of 900 GeV. In June came a short special run for the UA4 elastic scattering experiment. The main 1985 run got underway at the beginning of September, and when the 315 GeV beams were finally dumped on 23 December, the accumulated luminosity (a measure of the number of proton- antiproton collisions achieved) had reached a record figure of 655 inverse nanobarns, surpassing even the total number of collisions om all previous runs (0.2 inverse nanobarns in 1981, 28 in 1982, 153 in 1983 and 395 in 1984). Another great success last year was the smooth parallel running of the SPS Collider and the LEAR Low Energy Antiproton Ring. The main 1985 Collider run pro­ gressed in grand style with up to 1 70 nb" being recorded in a single Results from the UA 1 experiment at the week, while the superb Antiproton CERN proton-antiproton Collider show that Plenty of particles Accumulator scaled new heights the production of clusters or 'jets ' of In March last year, packets of 450 hadrons increases significantly over the of reliability, running at one stage energy range 200-900 GeV. GeV antiprotons orbiting in the for 999 hours (42 days) without seven-kilometre SPS ring at CERN the slightest mishap, notching up bilities.
    [Show full text]
  • FERMILAB New Neutrino Directions
    The HERA electron-proton collider now be­ ing built at the German DESY Laboratory in Hamburg will handle polarized (spin-oriented) electron beams. Here are some of the mova­ ble supports for the complicated spin rotator magnets, which will have to be moved up and down for different beam optics. Except for some minor work, all HERA civil engineering has been completed, and the bill is within one per cent of the original target figure, updated for inflation. FERMILAB New neutrino directions After two successful fixed target Tevatron runs in 1985 and 1987, the present neutrino programme at Fermilab has drawn to a close with the experiments agreeing with each other and with the faithful Standard Model. The long-standing discrepancy in the neutrino-nucleon reaction rate between studies at CERN and Fer­ milab has been resolved. Muon pairs, with each particle carrying the same electric charge, now ap­ pear at the prescribed rate, and the new 1987 data should go on to provide important new information on the quark content (structure functions) of nucleons. Thus it was an appropriate time to review the mented by additional quadrupoles magnet, transferred to the new ring data and examine possibilities for and multipoles. The 317 metre cir­ and accumulated there either in a the future in a 'New Directions in cumference DESY III, designed to single or nine equally spaced 'buck­ Neutrino Physics at Fermilab' meet­ take protons up to about 7.5 GeV, ets'. ing last fall. surrounds the new DESY II ma­ The electrons could then be The meeting got off to a good chine handling HERA electrons and taken up to 14 GeV without loss, start when Fermilab Director Leon positrons.
    [Show full text]