Formation of Photoelectron Holograms of Crystals Excited by Synchrotron Radiation V
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Investigation of the K-Mg-Ca Sulfate System As Part of Monitoring Problematic Phase Formations in † Renewable-Energy Power Plants
energies Article Investigation of the K-Mg-Ca Sulfate System as Part of Monitoring Problematic Phase Formations in y Renewable-Energy Power Plants Fiseha Tesfaye 1,* , Daniel Lindberg 2 , Mykola Moroz 3,4 and Leena Hupa 1 1 Johan Gadolin Process Chemistry Centre, Åbo Akademi University, Piispankatu 8, FI-20500 Turku, Finland; leena.hupa@abo.fi 2 Department of Chemical and Metallurgical Engineering, Aalto University, Kemistintie 1, FI-02150 Espoo, Finland; daniel.k.lindberg@aalto.fi 3 Department of Chemistry and Physics, National University of Water and Environmental Engineering, Soborna 11, UA-33028 Rivne, Ukraine; [email protected] 4 Department of Physical and Colloid Chemistry, Ivan Franko National University of Lviv, Kyrylo and Mefodiy 6, UA-79005 Lviv, Ukraine * Correspondence: fiseha.tesfaye@abo.fi; Tel.: +358-503-211-876 This article is an extension of our paper published in Materials Processing Fundamentals 2018, TMS 2018 y Conference; The Minerals, Metals & Materials Series. Springer, Cham, Switzerland, 11–15 March 2018; pp. 133–142. Received: 15 September 2020; Accepted: 11 October 2020; Published: 15 October 2020 Abstract: Besides the widely applied hydropower, wind farms and solar energy, biomass and municipal and industrial waste are increasingly becoming important sources of renewable energy. Nevertheless, fouling, slagging and corrosion associated with the combustion processes of these renewable sources are costly and threaten the long-term operation of power plants. During a high-temperature biomass combustion, alkali metals in the biomass fuel and the ash fusion behavior are the two major contributors to slagging. Ash deposits on superheater tubes that reduce thermal efficiency are often composed of complex combinations of sulfates and chlorides of Ca, Mg, Na, and K. -
Final Entries - Athletes List by Event
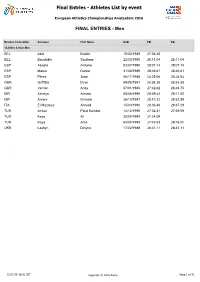
Final Entries - Athletes List by event European Athletics Championships Amsterdam 2016 FINAL ENTRIES - Men Member Federation Surname First Name DoB PB SB 10,000m Senior Men BEL Abdi Bashir 10/02/1989 27:36.40 BEL Bouchikhi Soufiane 22/03/1990 28:11.04 28:11.04 ESP Abadía Antonio 02/07/1990 28:07.14 28:07.14 ESP Mateo Daniel 31/08/1989 28:46.61 28:46.61 ESP Pérez Juan 06/11/1988 28:25.66 28:28.93 GBR Griffiths Dewi 09/08/1991 28:34.38 28:34.38 GBR Vernon Andy 07/01/1986 27:42.62 28:48.75 ISR Almeya Aimeru 08/06/1990 28:09.42 28:11.52 ISR Amare Girmaw 26/10/1987 28:10.32 28:52.89 ITA El Mazoury Ahmed 15/03/1990 28:36.40 28:37.29 TUR $UÕNDQ Polat Kemboi 12/12/1990 27:38.81 27:59.59 TUR Kaya Ali 20/04/1994 27:24.09 TUR Kaya Aras 04/04/1994 27:48.53 29:16.0h UKR Lashyn Dmytro 17/02/1988 28:37.11 28:37.11 01/07/16 16:42 CET Copyright © 2016 Arena Page 1 of 32 Final Entries - Athletes List by event European Athletics Championships Amsterdam 2016 FINAL ENTRIES - Men Member Federation Surname First Name DoB PB SB 100m Senior Men AUT Fuchs Markus 14/11/1995 10.36 10.36 BUL Dimitrov Denis 10/02/1994 10.16 10.18 CZE Veleba Jan 06/12/1986 10.23 10.28 ESP Hortelano Bruno 18/09/1991 10.06 10.06 ESP Rodríguez Ángel David 25/04/1980 10.14 10.24 EST Niit Marek 09/08/1987 10.19 10.30 FRA Dutamby Stuart 24/04/1994 10.12 10.12 FRA Lemaitre Christophe 11/06/1990 9.92 10.09 FRA Vicaut Jimmy 27/02/1992 9.86 9.86 FRA Zeze Mickael-Meba 19/05/1994 10.21 10.21 GBR Edoburun Ojie 02/06/1996 10.16 10.19 GBR Ellington James 06/09/1985 10.11 10.11 GBR Gemili Adam 06/10/1993 -

Ebook As Diasporas Dos Judeus E Cristaos.Pdf
As Diásporas dos Judeus e Cristãos- -Novos de Origem Ibérica entre o Mar Mediterrâneo e o Oceano Atlântico. Estudos ORGANIZAÇÃO : José Alberto R. Silva Tavim Hugo Martins Ana Pereira Ferreira Ângela Sofia Benoliel Coutinho Miguel Andrade Lisboa Centro de História da Universidade de Lisboa 2020 Título As Diásporas dos Judeus e Cristãos-Novos de Origem Ibérica entre o Mar Mediterrâneo e o Oceano Atlântico. Estudos Organização José Alberto R. Silva Tavim, Hugo Martins, Ana Pereira Ferreira, Ângela Sofia Benoliel Coutinho e Miguel Andrade Revisão André Morgado Comissão científica Ana Isabel Lopez-Salazar Codes (U. Complutense de Madrid), Anat Falbel (U. Federal do Rio de Janeiro), Ângela Domingues (U. Lisboa), Beatriz Kushnir (Directora, Arq. Geral da Cidade do Rio de Janeiro), Blanca de Lima (U. Francisco de Miranda, Coro; Acad. Nac. de la Historia-Capítulo Falcón, Venezuela), Claude B. Stuczynski (Bar-Ilan U.), Cynthia Michelle Seton-Rogers (U. of Texas-Dallas), Daniel Strum (U. São Paulo), Daniela Levy (U. São Paulo), Edite Alberto (Dep. Património Cultural/C. M. Lisboa; CHAM, FCSH-UNL), Elvira Azevedo Mea (U. Porto), Eugénia Rodrigues (U. Lisboa), Hernán Matzkevich (U. Purdue), Joelle Rachel Rouchou (Fund. Casa de Rui Barbosa, Rio de Janeiro), Jorun Poettering (Harvard U.), Maria Augusta Lima Cruz (ICS-U. do Minho; CHAM, FCSH, UNL), Maria Manuel Torrão (U. Lisboa), Moisés Orfali (Bar-Ilan U.), Nancy Rozenchan (U. de São Paulo), Palmira Fontes da Costa (U. Nova de Lisboa), Timothy D. Walker (U. Massachusetts Dartmouth) e Zelinda Cohen (Inst. do Património Cultural, Cabo Verde) Capa Belmonte, com Sinagoga Bet Eliahu. Fotografia de José Alberto R. -

Jewish Cemetries, Synagogues, and Mass Grave Sites in Ukraine
Syracuse University SURFACE Religion College of Arts and Sciences 2005 Jewish Cemetries, Synagogues, and Mass Grave Sites in Ukraine Samuel D. Gruber United States Commission for the Preservation of America’s Heritage Abroad Follow this and additional works at: https://surface.syr.edu/rel Part of the Religion Commons Recommended Citation Gruber, Samuel D., "Jewish Cemeteries, Synagogues, and Mass Grave Sites in Ukraine" (2005). Full list of publications from School of Architecture. Paper 94. http://surface.syr.edu/arc/94 This Report is brought to you for free and open access by the College of Arts and Sciences at SURFACE. It has been accepted for inclusion in Religion by an authorized administrator of SURFACE. For more information, please contact [email protected]. JEWISH CEMETERIES, SYNAGOGUES, AND MASS GRAVE SITES IN UKRAINE United States Commission for the Preservation of America’s Heritage Abroad 2005 UNITED STATES COMMISSION FOR THE PRESERVATION OF AMERICA’S HERITAGE ABROAD Warren L. Miller, Chairman McLean, VA Members: Ned Bandler August B. Pust Bridgewater, CT Euclid, OH Chaskel Besser Menno Ratzker New York, NY Monsey, NY Amy S. Epstein Harriet Rotter Pinellas Park, FL Bingham Farms, MI Edgar Gluck Lee Seeman Brooklyn, NY Great Neck, NY Phyllis Kaminsky Steven E. Some Potomac, MD Princeton, NJ Zvi Kestenbaum Irving Stolberg Brooklyn, NY New Haven, CT Daniel Lapin Ari Storch Mercer Island, WA Potomac, MD Gary J. Lavine Staff: Fayetteville, NY Jeffrey L. Farrow Michael B. Levy Executive Director Washington, DC Samuel Gruber Rachmiel -
Jewish Cemeteries, Synagogues, and Mass Grave Sites in Ukraine
JEWISH CEMETERIES, SYNAGOGUES, AND MASS GRAVE SITES IN UKRAINE United States Commission for the Preservation of America’s Heritage Abroad 2005 UNITED STATES COMMISSION FOR THE PRESERVATION OF AMERICA’S HERITAGE ABROAD Warren L. Miller, Chairman McLean, VA Members: Ned Bandler August B. Pust Bridgewater, CT Euclid, OH Chaskel Besser Menno Ratzker New York, NY Monsey, NY Amy S. Epstein Harriet Rotter Pinellas Park, FL Bingham Farms, MI Edgar Gluck Lee Seeman Brooklyn, NY Great Neck, NY Phyllis Kaminsky Steven E. Some Potomac, MD Princeton, NJ Zvi Kestenbaum Irving Stolberg Brooklyn, NY New Haven, CT Daniel Lapin Ari Storch Mercer Island, WA Potomac, MD Gary J. Lavine Staff: Fayetteville, NY Jeffrey L. Farrow Michael B. Levy Executive Director Washington, DC Samuel Gruber Rachmiel Liberman Research Director Brookline, MA Katrina A. Krzysztofiak Laura Raybin Miller Program Manager Pembroke Pines, FL Patricia Hoglund Vincent Obsitnik Administrative Officer McLean, VA 888 17th Street, N.W., Suite 1160 Washington, DC 20006 Ph: ( 202) 254-3824 Fax: ( 202) 254-3934 E-mail: [email protected] May 30, 2005 Message from the Chairman One of the principal missions that United States law assigns the Commission for the Preservation of America’s Heritage Abroad is to identify and report on cemeteries, monuments, and historic buildings in Central and Eastern Europe associated with the cultural heritage of U.S. citizens, especially endangered sites. The Congress and the President were prompted to establish the Commission because of the special problem faced by Jewish sites in the region: The communities that had once cared for the properties were annihilated during the Holocaust. -

Development and Application of Geochronometric Techniques to the Study of Sierra Nevada Uplift and the Dating of Authigenic Sediments
DEVELOPMENT AND APPLICATION OF GEOCHRONOMETRIC TECHNIQUES TO THE STUDY OF SIERRA NEVADA UPLIFT AND THE DATING OF AUTHIGENIC SEDIMENTS by M. Robinson Cecil _________________________________ A dissertation submitted to the faculty of the DEPARTMENT OF GEOSCIENCES In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY In the Graduate College UNIVERSITY OF ARIZONA 2009 2 THE UNIVERSITY OF ARIZONA GRADUATE COLLEGE As members of the Dissertation Committee, we certify that we have read the dissertation prepared by M. Robinson Cecil entitled Development and Application of Geochronometric Techniques to the Study of Sierra Nevada Uplift and the Dating of Authigenic Sediments and recommend that it be accepted as fulfilling the dissertation requirement for the Degree of Doctor of Philosophy ___________________________________________________________Date: 4/28/09 Mihai Ducea ___________________________________________________________Date: 4/28/09 Clement Chase ___________________________________________________________Date: 4/28/09 Jonathan Patchett ___________________________________________________________Date: 4/28/09 George Zandt ___________________________________________________________Date: 4/28/09 Paul Kapp Final approval and acceptance of this dissertation is contingent upon the candidate's submission of the final copies of the dissertation to the Graduate College. I hereby certify that I have read this dissertation prepared under my direction and recommend that it be accepted as fulfilling the dissertation requirement. ____________________________________________________________Date: 4/28/09 Dissertation Director: Mihai Ducea 3 STATEMENT BY AUTHOR This dissertation has been submitted in partial fulfillment of requirements for an advanced degree for the University of Arizona and is deposited in the University Library to be made available to borrowers under rules of the Library. Brief quotations from this dissertation are allowable without special permission, provided that accurate acknowledgment of source is made. -

Juliana Boerio-Goates Curriculum Vita
JULIANA BOERIO-GOATES CURRICULUM VITA Department of Chemistry Brigham Young University Provo, UT 84602 Education 1975 B.A. (Summa Cum Laude), Seton Hill College (Greensburg, PA) 1977 M.S., The University of Michigan 1979 Ph.D., The University of Michigan Professional Experience July 2008 B present Board of Directors, International Association of Chemical Thermodynamics. Jan 1999-2006 Editorial Board, Journal of Chemical Thermodynamics, Academic Press. Sept-Dec. 1997 Senior Academic Visitor, Chemical Crystallography Laboratory, Oxford University, Oxford, England 1996-2001 Associate Director, Center for the Improvement of Teacher Education and Schooling 1995-1998 Karl G. Maeser Professor of General Education 1993-present Professor of Chemistry 1992-1995 Associate Dean, General and Honors Education 1989-1992 Director, Center for Chemical Thermodynamics, BYU Jan.-Aug. 1989 Visiting Scientist, Center for Materials Science Research, Massachusetts Institute of Technology 1987-1993 Associate Professor Chemistry, Brigham Young University 1982-1987 Assistant Professor of Chemistry, Brigham Young University 1980-1981 Postdoctoral Research Associate, University of Michigan Summer 1976 Research Associate, Argonne National Laboratory, Argonne, IL Honors and Awards Alcuin Fellowship in General Education, BYU, 2007-2009. Karl G. Maeser Distinguished Faculty Lecture, BYU 2005-2006 Distinguished Centurion, Distinguished Alumni, Greensburg Central Catholic High School, Greensburg, PA 2004 Outstanding Teacher, BYU College of Physical and Mathematical Sciences, 2004 Phi Kappa Phi Distinguished Faculty Award, BYU, 2002-2003 Academic Year Distinguished Woman in Science Lecture, BYU College of Physical and Mathematical Sciences, 2002 Y-Chem Professor of the Month (September 2002), BYU Chemistry Student Affiliates Karl G. Maeser Professor of General Education, 1995-1998 Participant in the Leadership Associates Program of the National Network for Educational Reform, 1995-1996 Outstanding Alumna, Seton Hill College, 1995 Karl G. -

MB Kupershteyn TOWN of BAR: Jewish Pages Through
1 M. B. Kupershteyn TOWN OF BAR: Jewish Pages Through The Prism Of Time Vinnytsia-2019 2 The publication was carried out with the financial support of the Charity Fund " Christians for Israel-Ukraine” K 92 M. B. Kupershteyn Town of Bar: Jewish Pages Through The Prism Of Time. - Vinnytsia: LLC "Nilan-LTD", 2019 - 344 pages. This book tells about the town of Bar, namely the life of the Jewish population through the prism of historical events. When writing this book archival, historical, memoir, public materials, historical and ethnographic dictionaries, reference books, works of historians, local historians, as well as memories and stories of direct participants, living witnesses of history, photos from the album "Old Bar" and from other sources were used. The book is devoted to the Jewish people of Bar, the history of contacts between ethnic groups, which were imprinted in the people's memory and monuments of material culture, will be of interest to both professionals and a wide range of readers who are not indifferent to the history of the Jewish people and its cultural traditions. Layout and cover design: L. M. Kupershtein Book proofer: A. M. Krentsina ISBN 978-617-7742-19-6 ©Kupers M. B., 2019 ©Nilan-LTD, 2019 3 Table of Contents INTRODUCTION ........................................................................... 5 HISTORICAL BAR .......................................................................... 7 FROM THE DEPTHS OF HISTORY .................................................. 32 SHTETL .................................................................................... -

A NSF Physics Frontier Center Annual Report 2005-2006
A NSF Physics Frontier Center Annual Report 2005-2006 June 29, 2006 i Table of Contents 1 Executive Summary 1 2 Research Accomplishments and Plans 4 2.a Major Research Accomplishments . 4 2.a.1 Research Highlights . 4 2.a.2 Detailed Research Activities: MRC I- Theory . 5 2.a.3 Detailed Research Activities: MRC II- Structures in the Uni- verse ..................................... 20 2.a.4 Detailed Research Activities: MRC III - Cosmic Radiation Backgrounds ................................ 24 2.a.5 Detailed Research Activities: MRC IV - Particles from Space . 28 2.a.6 References . 32 2.b Research Organizational Details . 33 2.c Plans for the Coming Year . 33 3 Publications, Awards and Technology Transfers 40 3.a List of Publications in Peer Reviewed Journals . 40 3.b List of Publications in Peer Reviewed Conference Proceedings . 48 3.c Invited Talks by Institute Members . 52 3.d Honors and Awards . 56 3.e Technology Transfer . 57 4 Education and Human Resources 58 4.a Graduate and Postdoctoral Training . 58 4.a.1 Research Training . 58 4.a.2 Curriculum Development: . 62 4.b Undergraduate Education . 63 4.b.1 Undergraduate Research Experiences: . 63 4.b.2 Undergraduate Curriculum Development: . 64 4.c Educational Outreach . 65 4.c.1 K-12 Programs: Space Explorers . 66 4.c.2 Web-Based Educational Activities: . 69 4.c.3 Other: . 69 4.d Enhancing Diversity . 72 5 Community Outreach and Knowledge Transfer 74 5.a Visitor Participation in Center . 74 5.a.1 Long term visitors . 74 5.a.2 Short term and seminar visitors . 75 5.b Workshops and Symposia . -
Problems of Planetology, Cosmochemistry and Meteoritica
Abstracts Experimental geoecology Martynov1 K.V., Zakharova1 E.V., Nekrasov2 from the biosphere in rocks of earth crust. So far the A.N., Kotelnikov2 A.R. Influence of cooling only industrial technology of liquid HLW rate of the phosphate melt on phase solidification in our country is their processing in composition and properties of its phosphate glass at PA "Mayak". The composition, solidification products structure and properties of phosphate glasses are defined not only by the composition and temperature 1A.N. Frumkin Institutee of Physical Chemistry and conditions of melting of furnace mixture, but also by Electrochemistry RAS, Moscow mode of melt cooling [Vashman, 1997]. Really, a 2Institute of Experimental Mineralogy RAS, Chernogolovka cooling rate of a melt is easily regulated in vitro, and Moscow district for receiving homogeneous glass without crystal Abstract. It is experimentally proved that at slow cooling of inclusions it is tried to support highest rate (a Na2O-Al2O3-P2O5 melt used for a solidification of liquid high level quenching method). At PA "Mayak" spilling of waste (HLW) in glass matrix the glass-crystal product can be o formed. In process of fall of temperature in model experiments phosphate melt is made at a temperature 850 C from partial crystallization of melt was followed by differentiation of EP-500 ceramic furnace into cans with a capacity of main glass-forming components and HLW simulators between the 220 l [Polyakov, 1994]. The valuation by Newton- coexisting phases: Al, Cr, Fe concentrated in a crystal phase Na (Al,Cr,Fe) (P O ) PO ; Ca, Ni, La, U collected in the residual Rikhman’s heat equation shows that after spilling, 7 4 2 7 4 4 o melt as a result transformed to glass. -

Proceedings.Pdf
PEDIATRIC PULMONOLOGY PEDIATRIC ISSN 8755-6863 VOLUME 52 SUPPLEMENT 46 JUNE 2017 PEDIATRIC PULMONOLOGY Volume 52 • Supplement 46 • June 2017 Proceedings S1 Foreword PEDIATRIC PULMONOLOGY S2 Keynote Speaker S4 Post Graduate Course S17 I. Plenary Sessions S32 II. Topic Sessions S94 III. Young Investigator Oral Communications S100 IV. Posters S177 Index Volume 52 Supplement 46 June 2017 52 Supplement 46 June Volume 16th International Congress of Pediatric Pulmonology Lisbon Portugal, June 22–25, 2017 Pages S1 –S182 Pages ONLINE SUBMISSION AND PEER REVIEW http://mc.manuscriptcentral.com/ppul PEDIATRIC PULMONOLOGY Editor-in-Chief: THOMAS MURPHY, Watertown, MA USA Deputy Editor: TERRY NOAH, Chapel Hill, NC USA Associate Editors: ANNE CHANG, Brisbane, Queensland, Australia STEPHANIE DAVIS, Indianapolis, IN USA ALEXANDER MOELLER, Zurich, Switzerland KUNLING SHEN, Beijing, China PAUL STEWART, Chapel Hill, NC USA STEVEN TURNER, Aberdeen, Scotland, United Kingdom Topic Editors: JUDITH VOYNOW, Richmond, VA USA HEATHER ZAR, Cape Town, South Africa Managing Editor: ELIZABETH BRENNER, Malden, MA USA Editorial Board Richard Auten Brigitte Fauroux Min Lu Jürgen Schwarze Durham, NC USA Paris, France Shanghai, China Edinburgh, Scotland Avi Avital Michael Fayon George B. Mallory, Jr. Hiran Selvadurai Bordeaux, France Houston, TX USA Jerusalem, Israel Sydney, Australia Ian Balfour-Lynn Shona Fielding Franc¸ois Marchal Aberdeen, Scotland Nancy, France Renato Stein London, UK Porto Alegre, Brazil Monika Gappa Susanna McColley Eugenio Baraldi Wesel, Germany Chicago, IL USA Mary Sunday Padova, Italy Ben Gaston Mark Montgomery Durham, NC USA Lea Bentur Cleveland, OH USA Calgary, AB Canada Haifa, Israel Masato Takase Robert P. Gie Thomas Nicolai Tokyo, Japan David Birnkrant Tygerberg, South Africa Munich, Germany Cleveland, OH USA Asher Tal David Gozal Cathy Owens Beer-Sheva, Israel Hans Bisgaard Chicago, IL, USA London, UK Copenhagen, Denmark Anne Greenough Stacey Peterson-Carmichael Alejandro Teper Frank J. -

Adopting HIV/AIDS Policy in Russia and South Africa, 1999-2008
Syracuse University SURFACE Maxwell School of Citizenship and Public Political Science - Dissertations Affairs 2011 Treatment as a Common Good: Adopting HIV/AIDS Policy in Russia and South Africa, 1999-2008 Vladislav Kravtsov Syracuse University Follow this and additional works at: https://surface.syr.edu/psc_etd Part of the Political Science Commons Recommended Citation Kravtsov, Vladislav, "Treatment as a Common Good: Adopting HIV/AIDS Policy in Russia and South Africa, 1999-2008" (2011). Political Science - Dissertations. 97. https://surface.syr.edu/psc_etd/97 This Dissertation is brought to you for free and open access by the Maxwell School of Citizenship and Public Affairs at SURFACE. It has been accepted for inclusion in Political Science - Dissertations by an authorized administrator of SURFACE. For more information, please contact [email protected]. ABSTRACT The goal of this dissertation is to increase our understanding of domestic policy responses to initiatives and expertise as provided by international health organizations. Although following international recommendations often improves domestic public health, in certain circumstances resistance to adopting them persists. My core theoretical argument suggests that a strong societal agreement about what constitutes the ―common good‖ served by state (e.g., ―social purpose‖) informs how domestic policy-makers evaluate the benefits of adopting international recommendations. This agreement also affects how governments frame the provision of treatment, decide which subpopulations should benefit from the consumption of public good, and choose their partners in policy implementation. To demonstrate the impact of social purpose I examine how, why and with what consequences Russia and South Africa adopted the external best case practices, guidelines, and recommendations in regard to the HIV/AIDS treatment.