Linguistic Pitch Analysis Using Functional
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

第四届中国西南地区汉藏语国际研讨会program and Abstract Book
FOURTH WORKSHOP ON SINO-TIBETAN LANGUAGES OF SOUTHWEST CHINA 第四届中国西南地区汉藏语国际研讨会 UNIVERSITY OF WASHINGTON, SEATTLE SEPTEMBER 8-10, 2016 PROGRAM AND ABSTRACT BOOK Table of Contents General Information & Special Thanks to Our Sponsors ......................................................... 3 Program Synoptic Schedule ..................................................................................................................... 4 Thursday, September 8 .............................................................................................................. 5 Friday, September 9 ................................................................................................................... 6 Saturday, September 10 ............................................................................................................. 7 Abstracts (in presentation order) Scott DeLancey, Reconstructing Hierarchical Argument Indexation in Trans-Himalayan .... 8 James A. Matisoff, Lahu in the 21st century: vocabulary enrichment and orthographical issues ........................................................................................................................................ 10 Guillaume Jacques, The life cycle of multiple indexation and bipartite verbs in Sino-Tibetan ................................................................................................................................................. 11 Jackson T.-S. SUN and Qianzi TIAN, Argument Indexation patterns in Horpa languages: a major Rgyalrongic subgroup .................................................................................................. -

Prayer Cards | Joshua Project
Pray for the Nations Pray for the Nations A Che in China A'ou in China Population: 43,000 Population: 2,800 World Popl: 43,000 World Popl: 2,800 Total Countries: 1 Total Countries: 1 People Cluster: Tibeto-Burman, other People Cluster: Tai Main Language: Ache Main Language: Chinese, Mandarin Main Religion: Ethnic Religions Main Religion: Ethnic Religions Status: Unreached Status: Unreached Evangelicals: 0.00% Evangelicals: 0.00% Chr Adherents: 0.00% Chr Adherents: 0.00% Scripture: Translation Needed Scripture: Complete Bible www.joshuaproject.net Source: Operation China, Asia Harvest www.joshuaproject.net Source: Operation China, Asia Harvest "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations A-Hmao in China Achang in China Population: 458,000 Population: 35,000 World Popl: 458,000 World Popl: 74,000 Total Countries: 1 Total Countries: 2 People Cluster: Miao / Hmong People Cluster: Tibeto-Burman, other Main Language: Miao, Large Flowery Main Language: Achang Main Religion: Christianity Main Religion: Ethnic Religions Status: Significantly reached Status: Partially reached Evangelicals: 75.0% Evangelicals: 7.0% Chr Adherents: 80.0% Chr Adherents: 7.0% Scripture: Complete Bible Scripture: Complete Bible www.joshuaproject.net www.joshuaproject.net Source: Anonymous Source: Wikipedia "Declare his glory among the nations." Psalm 96:3 "Declare his glory among the nations." Psalm 96:3 Pray for the Nations Pray for the Nations Achang, Husa in China Adi -

A Speaker-Centered Approach to Descriptive Linguistics
Vol. 1, No. 2 (December 2007), pp.154-181 http://nflrc.hawaii.edu/ldc/ The Use of Perception Tests in Studying the Tonal System of Prinmi Dialects: A Speaker-centered Approach to Descriptive Linguistics Picus Sizhi Ding Macao Polytechnic Institute and University of Potsdam Contrary to previous description based on the Mandarin model of syllable-tone system, Xinyingpan, a dialect of Prinmi (a Tibeto-Burman language of China), has been discovered to possess a melody-tone system (or “pitch-accent” system) akin to that of Japanese. Targeting the crux of the unusual characteristics of this melody-tone system, where neutralization of two tonal categories in citation form is possible, this study uses perception tests to explore (dis)similarities among the tonal system of Xinyingpan Prinmi and those of other dialects. The perception tests consist of several minimal pairs of words contrasting solely by tone in a sentence frame. Results from more than twenty native speakers of fifteen Prinmi dialects from Ninglang, Lanping, and Yulong counties in Yunnan show that at least three minimal pairs of words in other dialects use the same tonal patterns for contrast in connected speech as in Xinyingpan. Evidence for the contrastive status of the pairs of words was attained directly from speakers who helped to prepare materials for the perception tests. This paper will also discuss some effects of language shift, such as linguistic attrition, observed in the empirical study. 1. INTRODUCTION1. Linguists doing fieldwork may observe fresh linguistic phenomena from time to time. Quite often, the new discovery is not shared with others who have worked on the same language at different times and locations. -

Reconsidering the Diachrony of Tone in Rma1
Journal of the Southeast Asian Linguistics Society JSEALS Vol. 13.1 (2020): 53-85 ISSN: 1836-6821, DOI: http://hdl.handle.net/10524/52460 University of Hawaiʼi Press RECONSIDERING THE DIACHRONY OF TONE IN RMA1 Nathaniel A. Sims University of California Santa Barbara [email protected] Abstract Prior work has suggested that proto-Rma was a non-tonal language and that tonal varieties underwent tonogenesis (Liú 1998, Evans 2001a-b). This paper re-examines the different arguments for the tonogenesis hypothesis and puts forward subgroup-internal and subgroup- external evidence for an alternative scenario in which tone, or its phonetic precursors, was present at the stage of proto-Rma. The subgroup-internal evidence comes from regular correspondences between tonal varieties. These data allow us to put forward a working hypothesis that proto-Rma had a two-way tonal contrast. Furthermore, existing accounts of how tonogenesis occurred in the tonal varieties are shown to be problematic. The subgroup-external evidence comes from regular tonal correspondences to two closely related tonal Trans- Himalayan subgroups: Prinmi, a modern language, and Tangut, a mediaeval language attested by written records from the 11th to 16th centuries. Regular correspondences among the tonal categories of these three subgroups, combined with the Rma-internal evidence, allow us to more confidently reconstruct tone for proto-Rma. Keywords: Tonogenesis, Trans-Himalayan (Sino-Tibetan), Rma, Prinmi, Tangut, Historical linguistics ISO 639-3 codes: qxs, pmi, pmj, txg 1. Introduction This paper addresses the diachrony of tone in Rma,2 a group of northeastern Trans-Himalayan3 language varieties spoken in 四川 Sìchuān, China. -

The Qiangic Subgroup from an Areal Perspective: a Case Study of Languages of Muli
LANGUAGE AND LINGUISTICS 13.1:133-170, 2012 2012-0-013-001-000299-1 The Qiangic Subgroup from an Areal Perspective: A Case Study of Languages of Muli Katia Chirkova CRLAO, CNRS In this paper, I study the empirical validity of the hypothesis of “Qiangic” as a subgroup of Sino-Tibetan, that is, the hypothesis of a common origin of thirteen little-studied languages of South-West China. This study is based on ongoing work on four Qiangic languages spoken in one locality (Muli Tibetan Autonomous County, Sichuan), and seen in the context of languages of the neighboring genetic subgroups (Yi, Na, Tibetan, Sinitic). Preliminary results of documentation work cast doubt on the validity of Qiangic as a genetic unit, and suggest instead that features presently seen as probative of the membership in this subgroup are rather the result of diffusion across genetic boundaries. I furthermore argue that the four local languages currently labeled Qiangic are highly distinct and not likely to be closely genetically related. Subsequently, I discuss Qiangic as an areal grouping in terms of its defining characteristics, as well as possible hypotheses pertaining to the genetic affiliation of its member languages currently labeled Qiangic. I conclude with some reflections on the issue of subgrouping in the Qiangic context and in Sino-Tibetan at large. Key words: Qiangic, classification, areal linguistics, Sino-Tibetan 1. Introduction This paper examines the empirical validity of the Qiangic subgrouping hypothesis, as studied in the framework of the project “What defines Qiang-ness: Towards a This is a reworked version of a paper presented at the International Symposium on Sino- Tibetan Comparative Studies in the 21st Century, held at the Institute of Linguistics, Academia Sinica, Taipei, Taiwan on June 24-25, 2010. -
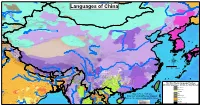
Map by Steve Huffman Data from World Language Mapping System 16
Mandarin Chinese Evenki Oroqen Tuva China Buriat Russian Southern Altai Oroqen Mongolia Buriat Oroqen Russian Evenki Russian Evenki Mongolia Buriat Kalmyk-Oirat Oroqen Kazakh China Buriat Kazakh Evenki Daur Oroqen Tuva Nanai Khakas Evenki Tuva Tuva Nanai Languages of China Mongolia Buriat Tuva Manchu Tuva Daur Nanai Russian Kazakh Kalmyk-Oirat Russian Kalmyk-Oirat Halh Mongolian Manchu Salar Korean Ta tar Kazakh Kalmyk-Oirat Northern UzbekTuva Russian Ta tar Uyghur SalarNorthern Uzbek Ta tar Northern Uzbek Northern Uzbek RussianTa tar Korean Manchu Xibe Northern Uzbek Uyghur Xibe Uyghur Uyghur Peripheral Mongolian Manchu Dungan Dungan Dungan Dungan Peripheral Mongolian Dungan Kalmyk-Oirat Manchu Russian Manchu Manchu Kyrgyz Manchu Manchu Manchu Northern Uzbek Manchu Manchu Manchu Manchu Manchu Korean Kyrgyz Northern Uzbek West Yugur Peripheral Mongolian Ainu Sarikoli West Yugur Manchu Ainu Jinyu Chinese East Yugur Ainu Kyrgyz Ta jik i Sarikoli East Yugur Sarikoli Sarikoli Northern Uzbek Wakhi Wakhi Kalmyk-Oirat Wakhi Kyrgyz Kalmyk-Oirat Wakhi Kyrgyz Ainu Tu Wakhi Wakhi Khowar Tu Wakhi Uyghur Korean Khowar Domaaki Khowar Tu Bonan Bonan Salar Dongxiang Shina Chilisso Kohistani Shina Balti Ladakhi Japanese Northern Pashto Shina Purik Shina Brokskat Amdo Tibetan Northern Hindko Kashmiri Purik Choni Ladakhi Changthang Gujari Kashmiri Pahari-Potwari Gujari Japanese Bhadrawahi Zangskari Kashmiri Baima Ladakhi Pangwali Mandarin Chinese Churahi Dogri Pattani Gahri Japanese Chambeali Tinani Bhattiyali Gaddi Kanashi Tinani Ladakhi Northern Qiang -

Tibet's Minority Languages-Diversity and Endangerment-Appendix 9 28 Sept Version
Tibet’s minority languages: Diversity and endangerment Short title: Tibet’s minority languages Authors: GERALD ROCHE (Asia Institute, University of Melbourne, [email protected])* HIROYUKI SUZUKI (IKOS, University of Oslo, [email protected]) Abstract Asia is the world’s most linguistically diverse continent, and its diversity largely conforms to established global patterns that correlate linguistic diversity with biodiversity, latitude, and topography. However, one Asian region stands out as an anomaly in these patterns—Tibet, which is often portrayed as linguistically homogenous. A growing body of research now suggests that Tibet is linguistically diverse. In this article, we examine this literature in an attempt to quantify Tibet’s linguistic diversity. We focus on the minority languages of Tibet—languages that are neither Chinese nor Tibetan. We provide five different estimates of how many minority languages are spoken in Tibet. We also interrogate these sources for clues about language endangerment among Tibet’s minority languages, and propose a sociolinguistic categorization of Tibet’s minority languages that enables broad patterns of language endangerment to be perceived. Appendices include lists of the languages identified in each of our five estimates, along with references to key sources on each language. Our survey found that as many as 60 minority languages may be spoken in Tibet, and that the majority of these languages are endangered to some degree. We hope out contribution inspires further research into the predicament of Tibet’s minority languages, and helps support community efforts to maintain and revitalize these languages. NB: This is the accepted version of this article, which was published in Modern Asian Studies in April 2018. -

The Influence of Mandarin Chinese on Minority Languages in Rural Southwest China: a Sociolinguistic Study of Tones in Contact
The influence of Mandarin Chinese on minority languages in rural southwest China: a sociolinguistic study of tones in contact JAMES N. STANFORD and JONATHAN P. EVANS Abstract Language change is often traced to language contact, but the specific socio linguistic processes are not fully understood. This article reports on our field research of contact between Chinese and two minority languages in rural southwest China: Sui and Qiang. The study shows how lexical tone, an under represented variable in sociolinguistics, can be valuable as an empirical mea sure of language contact and change. Furthermore, we find that it is the same Chinese tone, a high tone in Southwest Mandarin, which is affecting the pho nologies of both of these disparate minority languages. We use a social con structionist approach to model these changes: the “Structure” of a language is dialectically constructed by individual moments of speech — “Events” — which are in turn influenced by Structure. From this perspective, each indi vidual use of a hightone Chinese word is constructing and changing Sui and Qiang. Tone therefore provides an audible gauge of crosscultural contact, reflecting and constructing the rapidly changing sociolinguistic landscape of rural southwest China. Keywords: Language contact; tone; minority languages; Sui; Qiang. 1. Introduction The role of language contact is commonly noted in language change, but the social and linguistic complexity of such situations raises many questions about the specific processes involved. Thomason and Kaufman stress the importance of social factors, while also recognizing the secondary role of linguistic factors (1988: 212–213). With a similar sociolinguistic perspective in mind, we inves- tigate contact between Chinese and two minority languages in southwest China. -

Introduction to Qiang Phonology and Lexicon: Synchrony and Diachrony by Jonathan Paul Evans
Introduction to Qiang Phonology and Lexicon: Synchrony and Diachrony by Jonathan Paul Evans B.S. (Duke University) 1989 M.S. (University of California, Berkeley) 1991 A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Linguistics in the GRADUATE DIVISION of the UNIVERSITY OF CALIFORNIA, BERKELEY Committee in charge: Professor James A. Matisoff, Chairman Professor Gary B. Holland Professor Yoko Hasegawa FaH 1999 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Introduction to Qiang Phonology and Lexicon: Synchrony and Diachrony Copyright 1999 by Jonathan Paul Evans Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. This dissertation is dedicated to the greater glory of God A.M.D.G. and is offered here with deepest gratitude to My dear wife Wendy : I cannot imagine writing this without your patient endurance and gentle encouragement and to My wonderful parents, Hilary and Eunice Evans, who have waited a long time: May you continue to bless others as you have blessed me. and to The Qiang people, who have lavished on me their hospitality, patience, and friendship. "May God cause His face to shine upon you, and be gracious to you, and give you peace.” Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. In Memory of Elizabeth Evans 1965 - 1975 "...of such is the Kingdom of Heaven" Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Introduction to Qiang Phonology and Lexicon: Synchrony and Diachrony Table of Contents Abbreviations ...................................................................................................................... ix Acknowledgments ................................................................................................................ xi Chapter I. -

'African' Tone in the Sinosphere*
LANGUAGE AND LINGUISTICS 9.3:463-490, 2008 2008-0-009-003-000122-1 ‘African’ Tone in the Sinosphere* Jonathan P. Evans Academia Sinica Linguists often refer to tonal languages as belonging to ‘types’ ─ African, East Asian, etc. This paper documents the tonal system of the Mianchi dialect of Southern Qiang, a Tibeto-Burman language located squarely in the East Asian tone environment. Although tone has developed in Southern Qiang under heavy influence from Chinese, the tone system found in Mianchi fits an ‘African’ typology much better than it does a ‘Chinese’ or ‘East Asian’ type. The degrees of African-ness and Chinese-ness are evaluated, and African-style features are shown to be lurking throughout the Qiangic family. Similarities of word structure and word length between African and Qiangic languages are held responsible for the similarities. Key words: Tibeto-Burman, Qiang, tone typology, floating tone 1. Introduction Since Pike (1948), languages in which pitch is a non-predictable aspect of lexical items have been grouped into those in which level (or register) tones are basic, as is commonly found in Africa, and those in which contour tones are as basic as level tones, as in East Asia (Chinese dialects, Thai, Vietnamese, etc.). Recent research has elaborated on the typologies of ‘African’ tone (e.g., Odden 1995, Yip 2002:130-170, Hyman 2003, Downing 2004) and ‘East Asian’ tone (e.g., Matisoff 1999, Yip 1995, 2002:171-211). It is widely held that within the Qiang language (Tibeto-Burman: Qiangic; Sichuan Province, China), Southern dialects are lexically tonal and Northern dialects are not (H. -

Operation China
Qiang, Mawo October 9 ➤ GANSU hookworm to the Qiang, which has greatly reduced the danger of •Songpan Barkam these epidemic diseases. • •Maoxian •Wenchuan TIBET •Chengdu Customs: Qiang men and women •Litang •Kangding SICHUAN typically wear homespun linen Scale gowns with sheep-skin vests 0 KM 160 called guagua. They wear their Population in China: vests with the fur turned inward 12,000 (1990) for cool weather and turned 15,480 (2000) outward during rainy weather. 19,950 (2010) Location: Sichuan Both men and women wear Religion: Tibetan Buddhism variously colored scarfs on their Christians: None Known heads. Qiang women wear embroidered shoes called Yun Overview of the Yun shoes. An old legend says Mawo Qiang that long ago a Han girl named Yun Yun enjoyed close friendship Countries: China with her Qiang sisters and taught Pronunciation: “Chee-Ung-Mah-wo” them spinning, weaving, and Other Names: embroidery. One day Yun Yun and Chiang: Mawo, Mawo her Qiang sisters went up a Population Source: 12,000 (1998 mountain to cut firewood and got Liu Guangkun – 1990 figure); 15,000 (1998 J. Matisoff); caught in a storm; Yun Yun Out of a total Qiang population slipped and fell into a deep valley, of 198,252 (1990 census) leaving behind only her Location: W Sichuan: Heishui embroidered shoes. In memory of County: Mawo, Zhawo, Shuangliusuo, Xi’er, Hongyan, Yun Yun the Qiang girls wear and E’en districts Paul Hattaway shoes patterned after hers and Status: Location: In 1990 there were 12,000 call them Yun Yun shoes. Unmarried girls Officially included under Qiang speakers of the Mawo Qiang language often send their painstakingly embroidered Language: Sino-Tibetan, reported in China. -

2020 Daily Prayer Guide for All People Groups
2020 Daily Prayer Guide for all People Groups & Unreached People Groups of China Source: Joshua Project data, www.joshuaproject.net To order prayer resources or for inquiries, contact email: [email protected] 2020 Daily Prayer & Devotional Guide for all People Groups & LR-UPGs of China SUMMARY: China: 544 total People Groups; (+HK & Macau) China: 445 JP Least Reached = LR-UPG = shaded; Download & update from www.joshuaproject.net in July, Dec. 2019 LR-UPG: less than 2% Evangelical & less than 5% total Christian Frontier = FR = 0.1% Christian or less I give credit & thanks to Asia Harvest for permission to use their PG photos. Luke 10:2, Jesus told them, "The harvest is plentiful, but the workers are few. Ask the Lord of the harvest, therefore, to send out workers into his harvest field." * * * Let's dream God's dreams, and fulfill God's visions -- God dreams of all people groups knowing & loving Him! * * * Revelation 7:9, "After this I looked and there before me was a great multitude that no one could count, from every nation, tribe, people and language, standing before the throne and in front of the Lamb." CHINA -- DAILY PRAYER GUIDE FOR ALL PEOPLE GROUPS & UNREACHED PEOPLE GROUPS Page 1 PRAY PEOPLE GROUP POPULATION % - PERCENT % - PERCENT LR: PRIMARY PRIMARY PHOTOS OF DAILY: NAME: IN CHINA: EVANGELICAL: CHRISTIAN: FR LANGUAGE: RELIGION: PEOPLE GROUPS: 1 Jan. A Che 42,000 0 0 FR Ache Ethnic Religions 2 Jan. A'ou 2,800 0 0 FR A'ou Ethnic Religions 3 Jan. A-Hmao 455,000 75% 80% Miao,LargeFlowery Christianity 4 Jan.