Presentación De Powerpoint

Total Page：16

File Type：pdf, Size：1020Kb

La máquina de Turing No vamos a hablar de ALAN TURING Un poco de Historia Un poco de Historia 1812 Charles Babbage – Máquina diferencial Máquina calculadora de tablas matemáticas. La diseñó pero la construyó parcialmente. Cálculo de Funciones Polinómicas que aproximan a senos, cosenos, logaritmos, etc.. Un poco de Historia 1816-1871 Charles Babbage – Máquina Analítica Máquina analítica de propósito general. Sólo diseñó. Réplica en un museo de Londres Era programable con tarjetas perforadas. Lenguaje parecido a ensamblador. Ada Lovelace programadora. Un poco de Historia 1889 Herman Hollerith – Máquina Tabuladora Automatizó el censo americano Hollerith (ingeniero de minas) – Tabulating Machine Company 1890 - Tiempo de procesamiento humano 10 años, lo redujo a 6 semanas! Un poco de Historia 1936 Máquina de Turing Máquina universal abstracta http://www.aturingmachine.com/ Teoría de la computación que llevaría a la construcción del ordenador. Un poco de Historia 1939 Alan Turing - Bombe Dispositivo electro-mecánico. Descifrar códigos nazis de Enigma. 1920 – Enigma 1932 – Hitler gana elecciones & Marian Rejewski descifra códigos 1938 – Marian Rejewski diseña ‘Bombe’ 1939 – Alan Turing, Gordon Welchman y Harold Keen construyen ‘Bombe’ Parlamento Polaco a raiz de “The Imitation Game”: Controversia. La Máquina de Turing La máquina de Turing ¿Qué es un Número Computable? 1936 - Turing Un número computable es aquel para el que hay una máquina de Turing que dado un input termina con el n-ésimo dígito de ese número. Cálculo del número p Algoritmo de Chudnovsky ¿Qué es un Problema de decisión? ¿Es el 11 un número primo? ¿Es ababa un palíndromo? ¿Tardaré un tiempo finito en hacer un cálculo? 1936 - Church-Turing Demostraron que NO existe algoritmo general capaz de decidir si una fórmula es un TEOREMA. Problema de decisión = Problema de la parada 1936 - Turing Dada una máquina de Turing y un input, en general es imposible saber si la Máquina se parará. La máquina de Turing • Cinta con cuadrados. • Cada cuadrado es capaz de almacenar un símbolo del conjunto . • S es el input que pertenece al conjunto . • La máquina empieza que el input S . • Estado Inicial es q0 • En cada paso la máquina está en un estado q, lee un símbolo s, escribe un nuevo símbolo, cambia de estado y se mueve a la izquierda o derecha. q 0 1 1 0 0 1 1 1 0 0 1 0 1 0 0 0 La máquina de Turing • Formalmente una MAQUINA DE TURING es: función de transición input estados alfabeto q 0 1 1 0 0 1 1 1 0 0 1 0 1 0 0 0 Ejemplo Ejemplo de Código x 2x + 1 Números binarios x 2x + 1 Multiplicar por 2 un binario 3 x 2 = 6 4 x 2 = 8 Sumar 1 a un binario 3 + 1 = 4 6 + 1 = 7 Acabando… • 1931 – Gödel: “Toda teoría axiomática contiene proposiciones indecidibles: siempre habrá en ella afirmaciones verdaderas que no pueden demostrarse. • 1936 – Turing: Inicio oficial de la informática. Padre de la teoría de la computabilidad. • Aplicación en la Teoría de la complejidad. • La existencia de La máquina de Turing es en esencia la existencia de los algoritmos (ordenadores actuales) Gracias por vuestra atención .

281

Copy Link

Recommended publications

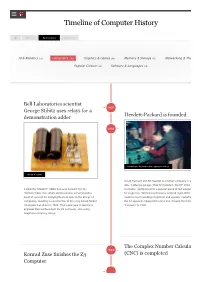
Timeline of Computer History
Timeline of Computer History By Year By Category Search AI & Robotics (55) Computers (145)(145) Graphics & Games (48) Memory & Storage (61) Networking & The Popular Culture (50) Software & Languages (60) Bell Laboratories scientist 1937 George Stibitz uses relays for a Hewlett-Packard is founded demonstration adder 1939 Hewlett and Packard in their garage workshop “Model K” Adder David Packard and Bill Hewlett found their company in a Alto, California garage. Their ﬁrst product, the HP 200A A Called the “Model K” Adder because he built it on his Oscillator, rapidly became a popular piece of test equipm “Kitchen” table, this simple demonstration circuit provides for engineers. Walt Disney Pictures ordered eight of the 2 proof of concept for applying Boolean logic to the design of model to test recording equipment and speaker systems computers, resulting in construction of the relay-based Model the 12 specially equipped theatres that showed the movie I Complex Calculator in 1939. That same year in Germany, “Fantasia” in 1940. engineer Konrad Zuse built his Z2 computer, also using telephone company relays. The Complex Number Calculat 1940 Konrad Zuse finishes the Z3 (CNC) is completed Computer 1941 The Zuse Z3 Computer The Z3, an early computer built by German engineer Konrad Zuse working in complete isolation from developments elsewhere, uses 2,300 relays, performs ﬂoating point binary arithmetic, and has a 22-bit word length. The Z3 was used for aerodynamic calculations but was destroyed in a bombing raid on Berlin in late 1943. Zuse later supervised a reconstruction of the Z3 in the 1960s, which is currently on Operator at Complex Number Calculator (CNC) display at the Deutsches Museum in Munich.
[Show full text]
Román Ceano © Román Ceano
La máquina enigma Román Ceano © Román Ceano. Todos los derechos reservados. El libro fue compilado de http://www.kriptopolis.org/enigma La fotografía sacada de http://enigma.wikispaces.com/file/view/enigma.jpg/30598271 Preludio En el verano de 1938, una pequeña localidad del condado de Buckingham vio perturbada su tranquilidad por la llegada de unos estrafalarios visitantes. Se trataba de hombres de aspecto próspero pero descuidado, acompañados por chicas que los lugareños juzgaron sospechosamente guapas y alegres. Estaban dirigidos al parecer por un tal Capitán Ridley, y decían que el motivo de su presencia era la caza. Ninguna de las camareras que les servían la cena en los hotelitos de la zona les oyó comentar anécdota cinegética alguna, lo cual era congruente con el hecho de que faltaban meses para la temporada. Lo que sí les oyeron comentar eran los opíparos almuerzos con que se obsequiaban. Estos debían tener lugar en la propiedad llamada Bletchley Park, puesto que allí se dirigían todos en sus coches cada mañana y de allí volvían cada tarde. Todo el mundo en Bletchley conocía la finca, sin duda la mejor de la comarca. La había creado sesenta años antes un exitoso corredor de bolsa de Londres llamado Herbert Leon, deseoso de disfrutar de la vida rural de las clases altas victorianas. Presidía la finca una mansión cuya fachada lucía una grotesca mezcla de estilos, que imitaba los palacios de las grandes familias rurales que habían sido reformados varias veces durante centurias. En la parte trasera había un gran patio, separado del edificio principal, donde estaban las cuadras, una enorme despensa donde guardar fruta fresca para el invierno y varias edificaciones auxiliares que recreaban de manera muy fidedigna el centro de operaciones de una propiedad rural.
[Show full text]
Bletchley Park, Haut Lieu De La Cryptographie
Bletchley Park, haut lieu de la cryptographie Laurent Bloch En route pour Bletchley Park! Bletchley Park est un site mythique de l’histoire de l’informatique: pendant la Seconde Guerre mondiale, Bletchley Park abrite le Government Code and Cypher School (GC&CS, qui deviendra le GCHQ en 1946), dont une mission de plus en plus importante sera le décryptement des messages codés des armées allemandes, et notamment des commu- nications des sous-marins en opérations dans l’Atlantique contre les convois qui achemi- naient de l’armement et d’autres marchandises vers le Royaume-Uni. À la ﬁn de la guerre, ce sont des dizaines de mathématiciens et d’ingénieurs qui travailleront à Bletch- ley Park, ainsi que plus de 8000 WRNS (British Women’s Royal Naval Service) occupées pour la plupart à transcrire les traces d’interceptions de transmissions hertziennes sur ruban perforé en vue de leur compilation et traitement sur matériel mécanographique. Ces opérations de décryptement, la recherche de procédés de nature à les automatiser, et la réalisation de machines capables de réaliser ces procédés, constituent des étapes majeures de la préhistoire de l’informatique, avec la participation d’Alan Turing, de Max Newman et d’autres précurseurs notables. Aussi, lorsque j’appris que l’ARCSI, dont j’ai l’honneur d’être membre, organisait une visite de Bletchley Park, je m’y précipitai, en entraînant mon épouse; en effet, lors de notre visite des collections d’ordinateurs du Science Museum de Londres, nous avions été frustrés de n’y voir ni la Bombe ni le Colossus. Ordinateur soviétique (Science Museum) Ça c’est de la logique discrète! Bletchley Park est à une heure de train de Londres-Euston, à 10 minutes à pied de la gare, c’est une excursion réalisable, que je ne saurais trop vous conseiller.
[Show full text]
Computer Hardware Lecture As of October 2014, There Were Nearly 2 Billion Personal Computers Used Worldwide
Computer Hardware Lecture As of October 2014, there were nearly 2 billion personal computers used worldwide. What is a Computer? A computer is an electronic (nowadays) device that processes information. To qualify as a computer a device must: • Accept Input • Remember and Store Information • Process Inputs • Produce Outputs LooKing at a Computer • Input: Your Keyboard and mouse, for example, are just input units—ways of getting information into your computer that it can process. If you use a microphone and voice recognition software, that's another form of input. • Memory/storage: Your computer probably stores all your documents and files on a hard-drive: a huge magnetic memory. But smaller, computer-based devices liKe digital cameras and cellphones use other Kinds of storage such as flash memory cards. • Processing: Your computer's processor (sometimes Known as the central processing unit) is a microchip buried deep inside. It worKs amazingly hard and gets incredibly hot in the process. That's why your computer has a little fan blowing away—to stop its brain from overheating! • Output: Your computer probably has an LCD screen capable of displaying high- resolution (very detailed) graphics, and probably also stereo loudspeakers. You may have an inKjet printer on your desK too to make a more permanent form of output. Computer History Charles Babbage (1791-1971) along with Ada Lovelace are credited with the invention of the first programmable computers. While Babbage's machines were mechanical and unwieldy, their basic architecture was similar to a modern computer. The data and program memory were separated, operation was instruction-based, the control unit could maKe conditional jumps, and the machine had a separate Input and Output unit.
[Show full text]
Contextualizing Colossus
Contextualizing Colossus: Codebreaking Technology and Institutional Capabilities (Preprint version) Thomas Haigh, University of Wisconsin—Milwaukee & Siegen University, [email protected] Mark Priestley, National Museum of Computing (UK), [email protected] This is a preprint draft. If you want to quote, cite, or assign this paper please use the final published version, which will appear in the July 2020 issue of Technology and Culture. Abstract: The Bletchley Park codebreaking center sits close to the heart of Britain’s collective sense of historical greatness. Historians view it as a highly successful but largely ad-hoc institutional response to novel cryptographic challenges, depicting both its reliance on elite mathematicians and a large labor force as ruptures with peacetime practice. In contrast, we suggest that underpinning Bletchley Park’s success were institutional capabilities established in the pre-war British state. We focus on the celebrated “Colossus” electronic codebreaking devices as one element of a highly successful institutional collaboration between Bletchley Park, where they were used, and the Post Office research station at Dollis Hill where they were designed and built. We reveal the development of a productive institutional partnership sponsored at the highest levels of government and supported by managers on both sides, correcting claims that Post Office engineer Tommy Flowers built the first machine at his own expense without the support or knowledge of Bletchley Park’s managers. Acknowledgements: This project was generously supported by Mrs. L. D. Rope’s Second Charitable Settlement. We extend our thanks to Crispin Rope and to all those at Lucy House. We are indebted to all those who commented on drafts of this, and related articles, including Brian Randell, Martin Campbell-Kelly, Quinn DuPont, Jim Reeds, Doron Swade, David Hemmendinger, Graeme Gooday, and the anonymous reviewers.
[Show full text]
Dongzu (Aidan) Lee 1 ANNOTATED BIBLIOGRAPHY1 Primary Sources
Dongzu (Aidan) Lee ANNOTATED BIBLIOGRAPHY1 Primary Sources Papers Turing, Alan. “Turing’s Treatise on Enigma.” (1939 - 1942) US National Archives and Records Administration. https://www.archives.gov/files/press/press-releases/2015/images/turing- enigma-treatise.pdf This paper had been written by Turing between 1939 and 1942 while working at Bletchley Park, but it had been classified for many years after the war by the British government; only in 1996 it became declassified. It is most informative on how Turing structured and manipulated input and algorithm in such ways as to maximize production of “contradictions” - for the purpose of skipping them - in Bombe, a computing machine he devised to deduce “rotor settings” from a given Enigma-encrypted message. What is the meaning of contradiction in Bombe? How to understand it best? A sign. An indication. An extra layer of information which neither True nor False solely as the answer(output) could deliver. Because of the way Bombe was set up, it communicated a unique meaning, and that was contradiction’s greatest use in Bombe. In the world of logic, contradiction often results from an inverted (i.e. up-side-down) self- inference such as in: “This statement is false.” (i.e. If it is true, it must be false, and if it is false, it must be true.) In the physical universe, a bridge may fall down if contradiction is present, because it means we have not fully thought out everything. In the world of Bombe, however, contradiction simply means randomness resulting from factors beyond the input – such as the rotor settings.
[Show full text]
“Alan Turing: the Journey of a Racing Mind” Vali Martinez Senior Division
“Alan Turing: The Journey of a Racing Mind” Vali Martinez Senior Division Individual Paper Word Count: 2,463 1 “Sometimes it is the people no one imagines anything of who do the things that no one can imagine.” 1 The Second World War persists in history as the most atrocious and utterly mortifying tragedy to befall globally. The malicious master Adolf Hitler banded with Germany, Italy, and Japan to coerce any individual set contumacious in his trail, continuously surmounting country after a helpless nation. In numerous circumstances, the advancements of the dictator's army were due to the German encryption mechanisms operating to transmit confidential combat communications. Striding forward to suffice the critical need of a penetrating mind to crack the seemingly impenetrable cryptograms, Alan Turing shined amidst the thousands that served to interpret reports from the prevalent German Enigma Machine. Turing's magnanimous wisdom drove him to vital contributions throughout the 20th-century conflict, and his lifelong benefactions to mathematics, in addition to the harsh penalty he sustained for existing as a homosexual individual, assisted in developing the position of such topics in modern-day society. Since boyhood, Turing displayed the prime demonstration of an extraordinary intellect. Born on June 23, 1912, in Maida Vale, London, the United Kingdom, the juvenile was raised with his older brother and mother (rarely witnessing the presence of his father, who was elsewhere in Chennai in the Indian Civil Service). 2 His inquisitiveness in science and biology first sparked at age ten when he received a novel with the title Nature’s Wonders .
[Show full text]
The History of Cracking the ENIGMA Machine
From Poznań to Bletchley Park : the history of cracking the ENIGMA machine: Marie-José Durand-Richard1 Philippe Guillot2 INTRODUCTION During World War II, the Allies could read many of the German ciphered messages they intercepted in plain text almost immediately, providing them with an advantage that had a significant impact on the course of the conflict. Movies such as Enigma (1999) and The Imitation Game (2015), highlight the success of the work of the British at Bletchley Park, and particularly the work of the mathematician Alan Madison Turing (1912-1954). But Turing did not work alone on breaking the Enigma code at Bletchley Park, and it is much less well-known that during the 1930s, the Poles had already accomplished the feat of making transparent the enciphered communications between the German army and its General Staff. So, the history of breaking the Enigma code is rather more complicated than is shown in such hagiographic movies. In this perspective, this paper focuses on the various skills at work in cracking the Enigma machine. In the period from 1932 to 1942, both the French and the British considered military intelligence would be more essential than mathematical cryptanalysis in overcoming the problem. However, their political and geographical situation stimulated the Poles to coordinate their technical, mathematical and political capabilities. Cyclometers, Bombas and perforated sheets were produced to help them overcome complications gradually introduced by the German armies in their Enigma ciphering methods. As early as 1936, the British codebreaker A. Dillwyn (Dilly) Knox (1884-1943) started a manual cryptanalysis of the commercial Enigma code at the Government Code and Cipher School (GC&CS) and succeeded in breaking the code of its Spanish and Italian versions in 1937.
[Show full text]
British Codebreaking Operations: 1938-43 Andrew J
East Tennessee State University Digital Commons @ East Tennessee State University Electronic Theses and Dissertations Student Works 5-2015 All the King’s Men: British Codebreaking Operations: 1938-43 Andrew J. Avery East Tennessee State University Follow this and additional works at: https://dc.etsu.edu/etd Part of the History Commons Recommended Citation Avery, Andrew J., "All the King’s Men: British Codebreaking Operations: 1938-43" (2015). Electronic Theses and Dissertations. Paper 2475. https://dc.etsu.edu/etd/2475 This Thesis - Open Access is brought to you for free and open access by the Student Works at Digital Commons @ East Tennessee State University. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of Digital Commons @ East Tennessee State University. For more information, please contact [email protected]. All the King’s Men: British Codebreaking Operations: 1938-43 _____________________ A thesis presented to the faculty of the Department of History East Tennessee State University In partial fulfillment of the requirements for the degree Master of Arts in History _____________________ by Andrew J. Avery May 2015 _____________________ Dr. Stephen G. Fritz, Chair Dr. Andrew L. Slap Dr. John Rankin Keywords: World War II, Alan Turing, Bletchley Park, Code-breaking, Room 40, Gordon Welchman, GC&CS ABSTRACT All the King’s Men: British Codebreaking Operations: 1938-43 by Andrew J. Avery The Enigma code was one of the most dangerous and effective weapons the Germans wielded at the outbreak of the Second World War. The Enigma machine was capable of encrypting radio messages that seemed virtually unbreakable.
[Show full text]
Cover Story Bletchley Park
eventy five years ago, Bletchley Park began work on deciphering German military messages. The story was shrouded in secrecy for nearly three Sdecades after the end of the Second World War and, even then, it filtered out slowly and reluctantly as some secrets still had currency. Many, especially those with an interest in technology, will recognise the name Alan Turing and associate him with the development of the first computer. However, such an association would earn a figurative rap on the knuckles from Bletchley historian Joel Greenberg. He acknowledged Turing’s genius, but pointed out that he was not at Bletchley Park when Colossus, the first electronic programmable computer, was designed and built. It has slowly emerged that Bletchley Park’s success – and it was huge – was down to a collective effort. While Colossus was the crowning glory from a technology perspective – it only became operational in the last year of the war – it was far from the only achievement. In fact, Colossus was only invented to decrypt messages sent using the Lorenz encryption machine, used in the latter part of the war for high level strategic communications. All operational communications during the entire conflict were made using Enigma machines machine encryption and Enigma was an electromechanical machine that and these were intercepted and decrypted successfully at Bletchley Park over performed alphabetic substitution, converting each character of a message the whole period. with another as randomly as possible. Greenberg explained: “Enigma was clumsy and unbelievably clunky. There Enigma and Bombe was a keyboard with 26 keys – one for each letter of the alphabet – and a Enigma was a commercial solution that, in earlier forms, had been around board with 26 circles of glass with a letter of alphabet embossed on it and a since World War I.
[Show full text]
C.S. PEIRCE, MECHANICALISM, and MUSIC by ARTHUR
C.S. PEIRCE, MECHANICALISM, AND MUSIC by ARTHUR FRANKLIN STEWART, B.A., M.M., M.M. A DISSERTATION IN FINE ARTS Submitted to the Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY Approved Accepted Dean (ff the Graduate School December, 1987 ^ /16 Ma. ^^"7 tor ^ Copyright 1987 Arthur Franklin Stewart CONTENTS ABSTRACT iii ILLUSTRATIONS v PREFACE vi I. AN OVERVIEW 1 II. WALTER GIESEKING AND ARTUR SCHNABEL: DIRECT EVIDENCE FROM THE MUSICAL WORLD 20 III. ALAN MARQUAND AND ALAN TURING: LOGICAL MACHINES, ALGORITHMS, AND FIXED METHODS . 5 0 IV. DAVID HILBERT AND CHARLES S. PEIRCE: FORMALISM AND THE LIMITS OF ROUTINE .... 79 REFERENCES 135 11 ABSTRACT C.S. Peirce, Mechanicalism, and Music is an interdisciplinary study which principally involves ideas drawn from music and philosophy. These ideas, as explored, propose useful interconnections between these areas of study. As the main point of philosophical reference, this examination uses aspects from the system of the eminent nineteenth-century American mathematician, scientist, and founder of philosophical pragmatism, Charles Sanders Peirce (1839-1914). Using the method of pragmatism as an overall guide, the present essay proposes the construction of a conceptually developed investigatory instrument to examine and test certain implications of the mechanical and anti-mechanical schools of thought found in the phenomenology of music, and to present from this examination a line of reasoning useful to the musical artist who seeks a rational choice between these schools. Writings by the pianists/teachers Walter Gieseking (1895-1956) and Artur Schnabel (1882-1951) are among the sources employed to illustrate aspects of the mechanical and anti-mechanical positions in music.
[Show full text]
Tutte, Flowers, and a Bad Imitation of Turing Reflections on Pioneering Code-Breaking Efforts
viewpoints VDOI:10.1145/3018994 Thomas Haigh Historical Reflections Colossal Genius: Tutte, Flowers, and a Bad Imitation of Turing Reflections on pioneering code-breaking efforts. AY 14, 2017, will be the 100th anniversary of the birth of someone you might not have heard of: William Thomas (“Bill”) Tutte. MDuring the Second World War he made several crucial contributions to decrypt- ing the Lorenz cipher used to protect the Nazi high command’s most cru- cial radio communications. This work provided the statistical method imple- mented electronically by Tommy Flow- ers, a telecommunications engineer, in the Colossus machines, which pio- neered many of the electronic engineer- ing techniques later used to build digi- tal computers and network equipment.a Myths of Bletchley Park The British code-breaking effort of the Second World War, formerly secret, is now one of the most celebrated aspects of modern British history, an inspiring story in which a free society mobilized its intellectual resources against a ter- rible enemy. That’s a powerful source of nostalgic pride for a country whose national identity and relationship with A scene from the 2014 film The Imitation Game with actor Benedict Cumberbatch its neighbors are increasingly uncertain. portraying Alan Turing. Tutte’s centennial gives a chance to con- sider the broader history of Bletchley and the way in which it has been remem- ably comes from the Oscar-winning Park, where the codebreakers worked, bered. Some kinds of people, and work, film The Imitation Game. This gives us have become famous and others have a starting point: the film is a bad guide not.
[Show full text]