DOCSLIB.ORG

Interior Point Methods ME575 – Optimization Methods John Hedengren

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Interior Point Methods ME575 – Optimization Methods John Hedengren Interior Point Methods ME575 – Optimization Methods John Hedengren 40 =0 30 =0.1 =1.0 ln(x) 20 =2.0 =5.0 10 =10 0 Barrier Function, Barrier - -10 -20 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Variable (x) Overview • Nonlinear constrained minimization • Slack variables • Barrier function • Newton’s method for KKT conditions • Interior Point Method (IPM) • Tutorial Examples Nonlinear Constrained Optimization min 푓(푥) 푥∈푅푛 푠. 푡. 푐 푥 = 0 푥 ≥ 0 • Linear, quadratic, or general nonlinear objective and constraints • Convex optimization, local solution possible for non-convex problems • Convert maximization by minimizing negative of the objective • Convert general inequalities to simple inequalities with slack variables Slack Variables min 푓(푥) min 푓(푥) 푥∈푅푛 푥∈푅푛 푠. 푡. 푔 푥 ≥ 푏 푠. 푡. 푐 푥 = 0 ℎ 푥 = 0 푥 ≥ 0 • Complete worksheet on slack variables 푚푛 푥1푥4 푥1 + 푥2 + 푥3 + 푥3 푥 푠. 푡. 푥1푥2푥3푥4 ≥ 25 2 2 2 2 푥1 + 푥2 + 푥3 + 푥4 = 40 • Additional slack variable tutorial: • http://apmonitor.com/me575/index.php/Main/SlackVariables Barrier Function 푛 min 푓(푥) min 푓 푥 − 휇 ෍ ln 푥푖 푥∈푅푛 푥∈푅푛 푠. 푡. 푐 푥 = 0 푖=1 푥 ≥ 0 푠. 푡. 푐 푥 = 0 40 • Natural log barrier term for =0 30 inequality constraints =0.1 =1.0 ln(x) 20 • The term ln 푥푖 is undefined=2.0 =5.0 10 for 푥푖 < 0 =10 0 • Search points only in interior Barrier Function, Barrier - -10 feasible space -20 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Variable (x) Barrier Function Example 1 min 푥 − 3 2 min 푥 − 3 2 − 휇 ln 푥 푥∈푅 푥∈푅 푠. 푡. 푥 ≥ 0 40 Unconstrained =1 30 =2 =5 =10 20 10 0 Augmented ObjectiveAugmented Function -10 -20 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Dependent Variable (x) Barrier Function Example 2 min 푥 + 1 2 min 푥 + 1 2 − 휇 ln 푥 푥∈푅 푥∈푅 푠. 푡. 푥 ≥ 0 10 Unconstrained 9 =1 8 =2 =5 7 =10 6 5 4 3 Augmented ObjectiveAugmented Function 2 1 0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 Dependent Variable (x) How to Solve a Barrier Problem: Step 1 • KKT Conditions for Barrier Problem 푛 푛 1 min푛 푓 푥 − 휇 ෍ ln 푥푖 훻푓 푥 + 훻푐 푥 휆 − 휇 ෍ = 0 푥∈푅 푥푖 푖=1 푖=1 푠. 푡. 푐 푥 = 0 푐 푥 = 0 1 • Define 푧푖 = and solve modified version of KKT conditions 푥푖 훻푓 푥 + 훻푐 푥 휆 − 푧 = 0 푐 푥 = 0 푋푍푒 − 휇푒 = 0 How to Solve a Barrier Problem: Step 2 • Find KKT solution with Newton-Raphson method 푥 훻푓 푥 + 훻푐 푥 휆 − 푧 = 0 푊푘 훻푐 푥푘 −퐼 푑푘 훻푓 푥푘 + 훻푐 푥푘 휆푘 − 푧푘 푐 푥 = 0 푇 휆 훻푐 푥푘 0 0 푑푘 = − 푐 푥푘 푋푍푒 − 휇푒 = 0 푧 푋 푍 푒 − 휇 푒 푍푘 0 푋푘 푑푘 푘 푘 푗 • Where: 푧1 0 0 푥1 0 0 2 2 푇 푊푘 = 훻푥푥퐿 푥푘, 휆푘, 푧푘 = 훻푥푥 푓 푥푘 + 푐 푥푘 휆푘 − 푧푘 푍푘 = 0 ⋱ 0 푋푘 = 0 ⋱ 0 0 0 푧푛 0 0 푥푛 Find a Search Direction and Step Size: Example 3 푑푥 푚푛 푓 = 푦2 푊푘 훻푐 푥푘 −퐼 푘 훻푓 푥푘 + 훻푐 푥푘 휆푘 − 푧푘 1 푇 휆 푥∈푅 훻푐 푥푘 0 0 푑푘 = − 푐 푥푘 푧 푋 푍 푒 − 휇 푒 푠. 푡. 2푦 ≤ 9 푍푘 0 푋푘 푑푘 푘 푘 푗 푦 ≥ 0 2 2 푇 푊푘 = 훻푥푥퐿 푥푘, 휆푘, 푧푘 = 훻푥푥 푓 푥푘 + 푐 푥푘 휆푘 − 푧푘 푠푡푎푟푡푛푔 푎푡 푦 = 3, 휇 = 10, 휆 = 1, 훼 = 0.5 How to Solve a Barrier Problem: Step 2 • Find KKT solution with Newton-Raphson method 푥 훻푓 푥 + 훻푐 푥 휆 − 푧 = 0 푊푘 훻푐 푥푘 −퐼 푑푘 훻푓 푥푘 + 훻푐 푥푘 휆푘 − 푧푘 푐 푥 = 0 푇 휆 훻푐 푥푘 0 0 푑푘 = − 푐 푥푘 푋푍푒 − 휇푒 = 0 푧 푋 푍 푒 − 휇 푒 푍푘 0 푋푘 푑푘 푘 푘 푗 • Where: 푧1 0 0 푥1 0 0 2 2 푇 푊푘 = 훻푥푥퐿 푥푘, 휆푘, 푧푘 = 훻푥푥 푓 푥푘 + 푐 푥푘 휆푘 − 푧푘 푍푘 = 0 ⋱ 0 푋푘 = 0 ⋱ 0 0 0 푧 0 0 푥 • Rearrange into symmetric linear system 푛 푛 푥 푊푘 + Σ푘 훻푐 푥푘 푑푘 훻푓 푥푘 + 훻푐 푥푘 휆푘 −1 푇 휆 = − Σ푘 = 푋푘 푍푘 훻푐 푥푘 0 푑푘 푐 푥푘 푧 푥 휆 • Solve for 푑푘 after the linear solution to 푑푘 and 푑푘 with explicit solution 푧 −1 푥 푑푘 = 휇푘푋푘 푒 − 푧푘 − Σ푘푑푘 Step Size (훼) • Two objectives in evaluating progress • Minimize objective • Minimize constraint violations • Two popular approaches • Decrease in merit function, 푚푒푟푡 = 푓 푥 + 휈 σ 푐(푥) • Filter methods • Cut back step size until improvement 푥 푥푘+1 = 푥푘 + 훼푘푑푘 휆 휆푘+1 = 휆푘 + 훼푘푑푘 푧 푧푘+1 = 푧푘 + 훼푘푑푘 Convergence Criteria • Convergence when KKT conditions are satisfied with a tolerance max 훻푓 푥 + 훻푐 푥 휆 − 푧 ≤ 휖푡표푙 max 푐(푥) ≤ 휖푡표푙 max 푋푍푒 − 휇푒 ≤ 휖푡표푙 • Tolerance for constraint violation may be more restrictive Interior Point Method Overview Initialize 휆 Initialize x , l , z 푥 = 푓푒푎푠푏푙푒 0 0 0 0 휇 퐼 훻푐 푥0 푤 훻푓 푥 − 푧 − 푧 푧0 = 0 퐿,0 푈,0 푥 푇 휆 = − 0 훻푐 푥0 0 0 0 Yes Check for Convergence Optimal Solution No 퐸 푥, 휆, 푧 ≤ 휖푡표푙 푥 Compute the Search Direction −1 푊푘 + Σ푘 훻푐 푥푘 푑푘 훻푓 푥푘 + 훻푐 푥푘 휆푘 − 푍푘 Σ푘 = 푋푘 푍푘 푇 휆 = − with the linearized Barrier Problem 훻푐 푥푘 0 푑푘 푐(푥푘) 푧 −1 푥 푑푘 = 휇푋푘 푒 − 푧푘 − Σ푘푑푘 푥 Backtracking Line Search 푥푘+1 = 푥푘 + 훼푘푑푘 Determine 훼 by decrease in Merit Function or 휆 = 휆 + 훼 푑휆 푘+1 푘 푘 푘 with Filter Methods 푧 푧푘+1 = 푧푘 + 훼푘푑푘 Barrier Function Example 4 푚푛 푥2 5 + 푥1 푥∈푅2 푥1푥2 ≥ 5 푠. 푡. 2 2 푥1 + 푥2 ≤ 20 Barrier Function: Example 4 min 푥2 5 + 푥1 푥∈푅2 푥1푥2 ≥ 5 푠. 푡. 2 2 푥1 + 푥2 ≤ 20 Comparing Interior Point and Active Set Methods 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) Percentage 6.1 40 MINOS 5.5 30 20 NLP Benchmark – Summary (494 Problems) 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than the best solver () APOPT Solver • AMPL / MATLAB / Python Interfaces from http://apopt.com IPOPT Solver • Download Source Code from https://projects.coin-or.org/Ipopt Interior Point Homework Problem 1 2 2 min 푥1 − 2푥1푥2 + 4푥2 푥∈푅2 푠. 푡. 0.1푥1 − 푥2 > 1 Interior Point Homework Problem 2 2 2 min 푥1 + 2푥2 푥∈푅2 푠. 푡. 2푥1 + 푥2 ≤ 9 푥1 + 2푥2 푥1 > 0, 푥2 > 0 Homework Help: IPOPT Output • Visit: http://apmonitor.com/online/view_pass.php?f=ipm.apm Homework Help: IPOPT Output IPOPT Output Headings • iter: The current iteration count. • objective: The unscaled objective value at the current point. • inf_pr: The unscaled max constraint violation at the current point. • inf_du: The max scaled dual infeasibility at the current point. • lg(mu): log10 of the value of the barrier parameter m • ||d||: The infinity norm (max) of the primal step • lg(rg): log10 of the value of the regularization term for the Hessian of the Lagrangian. Dash (-) indicates that no regularization was done. • alpha_du: The stepsize for the dual variables • alpha_pr: The stepsize for the primal variables • ls: The number of backtracking line search steps Homework Help: IPOPT Output Homework Help • Download BPOPT Solver (MATLAB version) from Interior Point Page • http://apmonitor.com/me575/index.php/Main/InteriorPointMethod • Homework Problem 1 = BPOPT problem 10 • Homework Problem 2 = BPOPT problem 6 % load bpopt libraries addpath('bpopt') % Solve problem 1 prob = bp_create(10); % create problem sol = bpopt(prob); % solve problem.
Load more

Recommended publications
  • University of California, San Diego
    UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization .
    [Show full text]
  • Click to Edit Master Title Style
    Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than
    [Show full text]
  • Specifying “Logical” Conditions in AMPL Optimization Models
    Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual
    [Show full text]
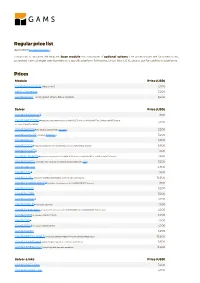
  • Standard Price List
    Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities .
    [Show full text]
  • Click to Edit Master Title Style
    Click to edit Master title style APMonitor Modeling Language John Hedengren Brigham Young University Advanced Process Solutions, LLC http://apmonitor.com Overview of APM Software as a service accessible through: MATLAB, Python, Web-browser interface Linux / Windows / Mac OS / Android platforms Solvers 1 1 2 3 3 APOPT , BPOPT , IPOPT , SNOPT , MINOS Problem characteristics: min J (x, y,u, z) Large-scale x s.t. 0 f , x, y,u, z Nonlinear Programming (NLP) t Mixed Integer NLP (MINLP) 0 g(x, y,u, z) Multi-objective 0 h(x, y,u, z) n m m Real-time systems x, y u z Differential Algebraic Equations (DAEs) 1 – APS, LLC 2 – EPL 3 – SBS, Inc. Oct 14, 2012 APMonitor.com Advanced Process Solutions, LLC Overview of APM Vector / matrix algebra with set notation Automatic Differentiation st nd Exact 1 and 2 Derivatives Large-scale, sparse systems of equations Object-oriented access Thermo-physical properties Database of preprogrammed models Parallel processing Optimization with uncertain parameters Custom solver or model connections Oct 14, 2012 APMonitor.com Advanced Process Solutions, LLC Unique Features of APM Initialization with nonlinear presolve minJ(x, y,u) x s.t. 0 f ,x, y,u min J (x, y,u) t 0 g(x, y,u) 0h(x, y,u) x minJ(x, y,u) x s.t. 0 f ,x, y,u s.t. 0 f , x, y,u t 0 g(x, y,u) t 0 h(x, y,u) minJ(x, y,u) x s.t. 0 f ,x, y,u t 0g(x, y,u) 0h(x, y,u) 0 g(x, y,u) minJ(x, y,u) x s.t.
    [Show full text]
  • Notes 1: Introduction to Optimization Models
    Notes 1: Introduction to Optimization Models IND E 599 September 29, 2010 IND E 599 Notes 1 Slide 1 Course Objectives I Survey of optimization models and formulations, with focus on modeling, not on algorithms I Include a variety of applications, such as, industrial, mechanical, civil and electrical engineering, financial optimization models, health care systems, environmental ecology, and forestry I Include many types of optimization models, such as, linear programming, integer programming, quadratic assignment problem, nonlinear convex problems and black-box models I Include many common formulations, such as, facility location, vehicle routing, job shop scheduling, flow shop scheduling, production scheduling (min make span, min max lateness), knapsack/multi-knapsack, traveling salesman, capacitated assignment problem, set covering/packing, network flow, shortest path, and max flow. IND E 599 Notes 1 Slide 2 Tentative Topics Each topic is an introduction to what could be a complete course: 1. basic linear models (LP) with sensitivity analysis 2. integer models (IP), such as the assignment problem, knapsack problem and the traveling salesman problem 3. mixed integer formulations 4. quadratic assignment problems 5. include uncertainty with chance-constraints, stochastic programming scenario-based formulations, and robust optimization 6. multi-objective formulations 7. nonlinear formulations, as often found in engineering design 8. brief introduction to constraint logic programming 9. brief introduction to dynamic programming IND E 599 Notes 1 Slide 3 Computer Software I Catalyst Tools (https://catalyst.uw.edu/) I AIMMS - optimization software (http://www.aimms.com/) Ming Fang - AIMMS software consultant IND E 599 Notes 1 Slide 4 What is Mathematical Programming? Mathematical programming refers to \programming" as a \planning" activity: as in I linear programming (LP) I integer programming (IP) I mixed integer linear programming (MILP) I non-linear programming (NLP) \Optimization" is becoming more common, e.g.
    [Show full text]
  • Treball (1.484Mb)
    Treball Final de Màster MÀSTER EN ENGINYERIA INFORMÀTICA Escola Politècnica Superior Universitat de Lleida Mòdul d’Optimització per a Recursos del Transport Adrià Vall-llaura Salas Tutors: Antonio Llubes, Josep Lluís Lérida Data: Juny 2017 Pròleg Aquest projecte s’ha desenvolupat per donar solució a un problema de l’ordre del dia d’una empresa de transports. Es basa en el disseny i implementació d’un model matemàtic que ha de permetre optimitzar i automatitzar el sistema de planificació de viatges de l’empresa. Per tal de poder implementar l’algoritme s’han hagut de crear diversos mòduls que extreuen les dades del sistema ERP, les tracten, les envien a un servei web (REST) i aquest retorna un emparellament òptim entre els vehicles de l’empresa i les ordres dels clients. La primera fase del projecte, la teòrica, ha estat llarga en comparació amb les altres. En aquesta fase s’ha estudiat l’estat de l’art en la matèria i s’han repassat molts dels models més importants relacionats amb el transport per comprendre’n les seves particularitats. Amb els conceptes ben estudiats, s’ha procedit a desenvolupar un nou model matemàtic adaptat a les necessitats de la lògica de negoci de l’empresa de transports objecte d’aquest treball. Posteriorment s’ha passat a la fase d’implementació dels mòduls. En aquesta fase m’he trobat amb diferents limitacions tecnològiques degudes a l’antiguitat de l’ERP i a l’ús del sistema operatiu Windows. També han sorgit diferents problemes de rendiment que m’han fet redissenyar l’extracció de dades de l’ERP, el càlcul de distàncies i el mòdul d’optimització.
    [Show full text]
  • GEKKO Documentation Release 1.0.1
    GEKKO Documentation Release 1.0.1 Logan Beal, John Hedengren Aug 31, 2021 Contents 1 Overview 1 2 Installation 3 3 Project Support 5 4 Citing GEKKO 7 5 Contents 9 6 Overview of GEKKO 89 Index 91 i ii CHAPTER 1 Overview GEKKO is a Python package for machine learning and optimization of mixed-integer and differential algebraic equa- tions. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP). Modes of operation include parameter regression, data reconciliation, real-time optimization, dynamic simulation, and nonlinear predictive control. GEKKO is an object-oriented Python library to facilitate local execution of APMonitor. More of the backend details are available at What does GEKKO do? and in the GEKKO Journal Article. Example applications are available to get started with GEKKO. 1 GEKKO Documentation, Release 1.0.1 2 Chapter 1. Overview CHAPTER 2 Installation A pip package is available: pip install gekko Use the —-user option to install if there is a permission error because Python is installed for all users and the account lacks administrative priviledge. The most recent version is 0.2. You can upgrade from the command line with the upgrade flag: pip install--upgrade gekko Another method is to install in a Jupyter notebook with !pip install gekko or with Python code, although this is not the preferred method: try: from pip import main as pipmain except: from pip._internal import main as pipmain pipmain(['install','gekko']) 3 GEKKO Documentation, Release 1.0.1 4 Chapter 2. Installation CHAPTER 3 Project Support There are GEKKO tutorials and documentation in: • GitHub Repository (examples folder) • Dynamic Optimization Course • APMonitor Documentation • GEKKO Documentation • 18 Example Applications with Videos For project specific help, search in the GEKKO topic tags on StackOverflow.
    [Show full text]
  • Largest Small N-Polygons: Numerical Results and Conjectured Optima
    Largest Small n-Polygons: Numerical Results and Conjectured Optima János D. Pintér Department of Industrial and Systems Engineering Lehigh University, Bethlehem, PA, USA [email protected] Abstract LSP(n), the largest small polygon with n vertices, is defined as the polygon of unit diameter that has maximal area A(n). Finding the configuration LSP(n) and the corresponding A(n) for even values n 6 is a long-standing challenge that leads to an interesting class of nonlinear optimization problems. We present numerical solution estimates for all even values 6 n 80, using the AMPL model development environment with the LGO nonlinear solver engine option. Our results compare favorably to the results obtained by other researchers who solved the problem using exact approaches (for 6 n 16), or general purpose numerical optimization software (for selected values from the range 6 n 100) using various local nonlinear solvers. Based on the results obtained, we also provide a regression model based estimate of the optimal area sequence {A(n)} for n 6. Key words Largest Small Polygons Mathematical Model Analytical and Numerical Solution Approaches AMPL Modeling Environment LGO Solver Suite For Nonlinear Optimization AMPL-LGO Numerical Results Comparison to Earlier Results Regression Model Based Optimum Estimates 1 Introduction The diameter of a (convex planar) polygon is defined as the maximal distance among the distances measured between all vertex pairs. In other words, the diameter of the polygon is the length of its longest diagonal. The largest small polygon with n vertices is the polygon of unit diameter that has maximal area. For any given integer n 3, we will refer to this polygon as LSP(n) with area A(n).
    [Show full text]
  • Users Guide for Snadiopt: a Package Adding Automatic Differentiation to Snopt∗
    USERS GUIDE FOR SNADIOPT: A PACKAGE ADDING AUTOMATIC DIFFERENTIATION TO SNOPT∗ E. Michael GERTZ Mathematics and Computer Science Division Argonne National Laboratory Argonne, Illinois 60439 Philip E. GILL and Julia MUETHERIG Department of Mathematics University of California, San Diego La Jolla, California 92093-0112 January 2001 Abstract SnadiOpt is a package that supports the use of the automatic differentiation package ADIFOR with the optimization package Snopt. Snopt is a general-purpose system for solving optimization problems with many variables and constraints. It minimizes a linear or nonlinear function subject to bounds on the variables and sparse linear or nonlinear constraints. It is suitable for large-scale linear and quadratic programming and for linearly constrained optimization, as well as for general nonlinear programs. The method used by Snopt requires the first derivatives of the objective and con- straint functions to be available. The SnadiOpt package allows users to avoid the time- consuming and error-prone process of evaluating and coding these derivatives. Given Fortran code for evaluating only the values of the objective and constraints, SnadiOpt automatically generates the code for evaluating the derivatives and builds the relevant Snopt input files and sparse data structures. Keywords: Large-scale nonlinear programming, constrained optimization, SQP methods, automatic differentiation, Fortran software. [email protected] [email protected] [email protected] http://www.mcs.anl.gov/ gertz/ http://www.scicomp.ucsd.edu/ peg/ http://www.scicomp.ucsd.edu/ julia/ ∼ ∼ ∼ ∗Partially supported by National Science Foundation grant CCR-95-27151. Contents 1. Introduction 3 1.1 Problem Types . 3 1.2 Why Automatic Differentiation? . 3 1.3 ADIFOR ......................................
    [Show full text]
  • Component-Oriented Acausal Modeling of the Dynamical Systems in Python Language on the Example of the Model of the Sucker Rod String
    Component-oriented acausal modeling of the dynamical systems in Python language on the example of the model of the sucker rod string Volodymyr B. Kopei, Oleh R. Onysko and Vitalii G. Panchuk Department of Computerized Mechanical Engineering, Ivano-Frankivsk National Technical University of Oil and Gas, Ivano-Frankivsk, Ukraine ABSTRACT Typically, component-oriented acausal hybrid modeling of complex dynamic systems is implemented by specialized modeling languages. A well-known example is the Modelica language. The specialized nature, complexity of implementation and learning of such languages somewhat limits their development and wide use by developers who know only general-purpose languages. The paper suggests the principle of developing simple to understand and modify Modelica-like system based on the general-purpose programming language Python. The principle consists in: (1) Python classes are used to describe components and their systems, (2) declarative symbolic tools SymPy are used to describe components behavior by difference or differential equations, (3) the solution procedure uses a function initially created using the SymPy lambdify function and computes unknown values in the current step using known values from the previous step, (4) Python imperative constructs are used for simple events handling, (5) external solvers of differential-algebraic equations can optionally be applied via the Assimulo interface, (6) SymPy package allows to arbitrarily manipulate model equations, generate code and solve some equations symbolically. The basic set of mechanical components (1D translational “mass”, “spring-damper” and “force”) is developed. The models of a sucker rods string are developed and simulated using these components. The comparison of results of the sucker rod string simulations with practical dynamometer cards and Submitted 22 March 2019 Accepted 24 September 2019 Modelica results verify the adequacy of the models.
    [Show full text]
  • A Case Study to Help You Think About Your Project
    Wind Turbine Optimization a case study to help you think about your project Andrew Ning ME 575 Three broad areas of optimization (with some overlap) Convex Gradient-Based Gradient-Free Today we will focus on gradient-based, but for some projects the other areas are more important. In higher dimensional space, analytic gradients become increasingly important #iterations # design vars There is a difference between developing for analysis vs optimization Vy(1 + a0) plane of rotation φ V (1 a) W x − There is a difference between developing for analysis vs optimization Vy(1 + a0) plane of rotation φ V (1 a) W x − 1 a 2 C = − c σ0 CT =4a(1 a) T sin φ n − ✓ ◆ 2 1+a0 2 2 C = c σ0λ CQ =4a0(1 + a0) tan φλ Q cos φ t r r ✓ ◆ There is a difference between developing for analysis vs optimization Vy(1 + a0) plane of rotation φ V (1 a) W x − 1 1 a = 2 a0 = 4sin φ +1 4sinφ cos φ 1 cnσ0 ctσ0 − There is a difference between developing for analysis vs optimization use Parameters y use ProgGen Converg Skew correction use WTP_Data n CALL GetCoefs Declarations reset induction !Converg & Return Initialize induction vars < MaxIter CALL FindZC CALL NewtRaph reset induction Initial guess (AxInd / TanInd) n & y CALL NewtRaph MaxIter ZFound Converg CALL BinSearch < Converg ! y n AxIndLo = AxInd -1 n AxIndHi = AxInd +1 AxIndLo = -0.5 Converg AxIndHi = 0.6 CALL BinSearch y n Skew correction Converg AxIndLo = -1.0 CALL BinSearch AxIndHi = -0.4 y CALL GetCoefs n Converg AxIndLo = 0.59 CALL BinSearch AxIndHi = 2.5 Return y y Converg Skew correction CALL GetCoefs Return n AxIndLo = -1.0 CALL BinSearch AxIndHi = 2.5 y Converg Skew correction CALL GetCoefs Return n Return Sometimes a new solution approach is needed… Vy(1 + a0) plane of rotation φ Vx(1 a) W − sin φ V cos φ (φ)= x =0 R 1 a − V (1 + a ) − y 0 Sometimes a new solution approach is needed… Algorithm Avg.
    [Show full text]