Microwave Measurements of the Time Evolution of Electron Density in the T-11M Tokamak V
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Warfare in a Fragile World: Military Impact on the Human Environment
Recent Slprt•• books World Armaments and Disarmament: SIPRI Yearbook 1979 World Armaments and Disarmament: SIPRI Yearbooks 1968-1979, Cumulative Index Nuclear Energy and Nuclear Weapon Proliferation Other related •• 8lprt books Ecological Consequences of the Second Ihdochina War Weapons of Mass Destruction and the Environment Publish~d on behalf of SIPRI by Taylor & Francis Ltd 10-14 Macklin Street London WC2B 5NF Distributed in the USA by Crane, Russak & Company Inc 3 East 44th Street New York NY 10017 USA and in Scandinavia by Almqvist & WikseH International PO Box 62 S-101 20 Stockholm Sweden For a complete list of SIPRI publications write to SIPRI Sveavagen 166 , S-113 46 Stockholm Sweden Stoekholol International Peace Research Institute Warfare in a Fragile World Military Impact onthe Human Environment Stockholm International Peace Research Institute SIPRI is an independent institute for research into problems of peace and conflict, especially those of disarmament and arms regulation. It was established in 1966 to commemorate Sweden's 150 years of unbroken peace. The Institute is financed by the Swedish Parliament. The staff, the Governing Board and the Scientific Council are international. As a consultative body, the Scientific Council is not responsible for the views expressed in the publications of the Institute. Governing Board Dr Rolf Bjornerstedt, Chairman (Sweden) Professor Robert Neild, Vice-Chairman (United Kingdom) Mr Tim Greve (Norway) Academician Ivan M£ilek (Czechoslovakia) Professor Leo Mates (Yugoslavia) Professor -

Large Igneous Provinces: a Driver of Global Environmental and Biotic Changes, Geophysical Monograph 255, First Edition
2 Radiometric Constraints on the Timing, Tempo, and Effects of Large Igneous Province Emplacement Jennifer Kasbohm1, Blair Schoene1, and Seth Burgess2 ABSTRACT There is an apparent temporal correlation between large igneous province (LIP) emplacement and global envi- ronmental crises, including mass extinctions. Advances in the precision and accuracy of geochronology in the past decade have significantly improved estimates of the timing and duration of LIP emplacement, mass extinc- tion events, and global climate perturbations, and in general have supported a temporal link between them. In this chapter, we review available geochronology of LIPs and of global extinction or climate events. We begin with an overview of the methodological advances permitting improved precision and accuracy in LIP geochro- nology. We then review the characteristics and geochronology of 12 LIP/event couplets from the past 700 Ma of Earth history, comparing the relative timing of magmatism and global change, and assessing the chronologic support for LIPs playing a causal role in Earth’s climatic and biotic crises. We find that (1) improved geochronol- ogy in the last decade has shown that nearly all well-dated LIPs erupted in < 1 Ma, irrespective of tectonic set- ting; (2) for well-dated LIPs with correspondingly well-dated mass extinctions, the LIPs began several hundred ka prior to a relatively short duration extinction event; and (3) for LIPs with a convincing temporal connection to mass extinctions, there seems to be no single characteristic that makes a LIP deadly. Despite much progress, higher precision geochronology of both eruptive and intrusive LIP events and better chronologies from extinc- tion and climate proxy records will be required to further understand how these catastrophic volcanic events have changed the course of our planet’s surface evolution. -

Geologic Studies of Planetary Surfaces Using Radar Polarimetric Imaging 2
Geologic studies of planetary surfaces using radar polarimetric imaging 2 4 Lynn M. Carter NASA Goddard Space Flight Center 8 Donald B. Campbell 9 Cornell University 10 11 Bruce A. Campbell 12 Smithsonian Institution 13 14 14 Abstract: Radar is a useful remote sensing tool for studying planetary geology because it is 15 sensitive to the composition, structure, and roughness of the surface and can penetrate some 16 materials to reveal buried terrain. The Arecibo Observatory radar system transmits a single 17 sense of circular polarization, and both senses of circular polarization are received, which allows 18 for the construction of the Stokes polarization vector. From the Stokes vector, daughter products 19 such as the circular polarization ratio, the degree of linear polarization, and linear polarization 20 angle are obtained. Recent polarimetric imaging using Arecibo has included Venus and the 21 Moon. These observations can be compared to radar data for terrestrial surfaces to better 22 understand surface physical properties and regional geologic evolution. For example, 23 polarimetric radar studies of volcanic settings on Venus, the Moon and Earth display some 24 similarities, but also illustrate a variety of different emplacement and erosion mechanisms. 25 Polarimetric radar data provides important information about surface properties beyond what can 26 be obtained from single-polarization radar. Future observations using polarimetric synthetic 27 aperture radar will provide information on roughness, composition and stratigraphy that will 28 support a broader interpretation of surface evolution. 29 2 29 1.0 Introduction 30 31 Radar polarimetry has the potential to provide more information about surface physical 32 properties than single-polarization backscatter measurements, and has often been used in remote 33 sensing observations of Solar System objects. -

Case Study of the Internal Growth Dynamics of NASA
University of Montana ScholarWorks at University of Montana Graduate Student Theses, Dissertations, & Professional Papers Graduate School 1971 Case study of the internal growth dynamics of NASA Bruce M. Whitehead The University of Montana Follow this and additional works at: https://scholarworks.umt.edu/etd Let us know how access to this document benefits ou.y Recommended Citation Whitehead, Bruce M., "Case study of the internal growth dynamics of NASA" (1971). Graduate Student Theses, Dissertations, & Professional Papers. 1747. https://scholarworks.umt.edu/etd/1747 This Thesis is brought to you for free and open access by the Graduate School at ScholarWorks at University of Montana. It has been accepted for inclusion in Graduate Student Theses, Dissertations, & Professional Papers by an authorized administrator of ScholarWorks at University of Montana. For more information, please contact [email protected]. CASE STUDY OF THE INTERNAL GROWTH DYNAMICS OF NASA By Bruce M. Whitehead B.A. University of Montana, 1970 Presented in partial fulfillment of the requirements for the degree of Master of Arts UNIVERSITY OF MONTANA 1971 Approved by: Chairman, Board of Examiners Dea^ Grad^txe 7/ UMI Number: EP35189 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. UMI OlM«rt*tk>n Publishing UMI EP35189 Published by ProQuest LLC (2012). Copyright in the Dissertation held by the Author. -

All Roads in County (Updated January 2020)
All Roads Inside Deschutes County ROAD #: 07996 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) <null> <null> 211009 Other Rural Local Dirt-Graded <null> County Road Length: 0 101ST LN ROAD #: 02265 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) 10 0 101ST ST 0.262 END BULB 151204 Deschutes County Rural Local Macadam, Oil 0.262 Mat County Road Length: 0.262 101ST ST ROAD #: 02270 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) 10 0 HWY 126 0.357 MAPLE LN, NW 151204 Deschutes County Rural Local Macadam, Oil 0.357 Mat 20 0.357 MAPLE LN, NW 1.205 95TH ST 151203 Deschutes County Rural Local Macadam, Oil 0.848 Mat County Road Length: 1.205 103RD ST ROAD #: 02259 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) <null> <null> 151209 Local Access Road Rural Local AC <null> <null> <null> 151209 Unknown Rural Local AC <null> 40 2.75 BEGIN 3.004 COYNER AVE, 141228 Deschutes County Rural Local Macadam, Oil 0.254 NW Mat County Road Length: 0.254 105TH CT Page 1 of 975 \\Road\GIS_Proj\ArcGIS_Products\Road Lists\Full List 2020 DCRD Report 1/02/2020 ROAD #: 02261 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) 10 0 QUINCE AVE, NW 0.11 END BUBBLE 151204 Deschutes County Rural Local Macadam, Oil 0.11 Mat County Road Length: 0.11 10TH ST ROAD #: 02188 SEGMENT FROM TO TRS OWNER CLASS SURFACE LENGTH (mi) <null> <null> 151304 City of Redmond City Collector AC <null> <null> <null> 151309 City of Redmond City Local AC <null> <null> <null> 151304 City of Redmond City Collector Macadam, Oil <null> Mat <null> <null> 141333 City of Redmond Rural -

Arvalis Ross, S. Californica Banks, S. Cornuta Ross, S. Hamata Ross, S
AN ABSTRACT OF THE THESIS OF ELWIN D. EVANS for the DOCTOR OF PHILOSOPHY (Name) (Degree) in ENTOMOLOGY presented on October 4, 1971 (Major) (Date) Title: A STUDY OF THE MEGALOPTERA OF THE PACIFIC COASTAL REGION ,Or THE UNtjT5D STATES Abstract approved: N. H. /Anderson Nineteen species of Megaloptera occurring in the western United States and Canada were studied.In the Sialidae, the larvae of Sialis arvalis Ross, S. californica Banks, S. cornuta Ross, S. hamata Ross, S. nevadensis Davis, S. occidens Ross and S. rotunda Banks are described with a key for their identification.The female of S. arvalis is described for the first time.Descriptions of the egg masses, hatching, and the egg bursters and first instar larvae are givenfor some species.Data are given on larval habitats, life cycles, distribution and emergence of the adults. An evolutionaryscheme for the Sialidae in the study area and the world genera ishypothesized. In the Corydalidae, Orohermes gen. nov. andProtochauliodes cascadiusse.nov. are described.The adults of Corydalus cognatus Hagen, Dysmicohermes disjunctus Munroe, D. ingens Chandler, Orohermes crepusculus (Chandler), Neohermesfilicornis (Banks), N. californicus (Walker), Protochauliodes aridus Maddux, P. spenceri Munroe, P. montivagus.Chandler, P. simplus Chandler, and P. minimus (Davis) are also described.The larvae of all but three species are described.Keys are presented for identifying the adults and larvae.Egg masses, egg bursters and the mating behavior are given for some species.Pre-genital scent glands were found in the males of the Corydalidae.Data are given on the larval habitats, distribution and adult emergence.Life cycles of five years are estimated for some intermittent stream inhabitants and the cold stream species, 0. -

Summary of Sexual Abuse Claims in Chapter 11 Cases of Boy Scouts of America
Summary of Sexual Abuse Claims in Chapter 11 Cases of Boy Scouts of America There are approximately 101,135sexual abuse claims filed. Of those claims, the Tort Claimants’ Committee estimates that there are approximately 83,807 unique claims if the amended and superseded and multiple claims filed on account of the same survivor are removed. The summary of sexual abuse claims below uses the set of 83,807 of claim for purposes of claims summary below.1 The Tort Claimants’ Committee has broken down the sexual abuse claims in various categories for the purpose of disclosing where and when the sexual abuse claims arose and the identity of certain of the parties that are implicated in the alleged sexual abuse. Attached hereto as Exhibit 1 is a chart that shows the sexual abuse claims broken down by the year in which they first arose. Please note that there approximately 10,500 claims did not provide a date for when the sexual abuse occurred. As a result, those claims have not been assigned a year in which the abuse first arose. Attached hereto as Exhibit 2 is a chart that shows the claims broken down by the state or jurisdiction in which they arose. Please note there are approximately 7,186 claims that did not provide a location of abuse. Those claims are reflected by YY or ZZ in the codes used to identify the applicable state or jurisdiction. Those claims have not been assigned a state or other jurisdiction. Attached hereto as Exhibit 3 is a chart that shows the claims broken down by the Local Council implicated in the sexual abuse. -

Lunar Polar Craters--Icy, Rough Or Just Sloping?
Lunar polar craters – icy, rough or just sloping? Vincent R. Ekea,∗, Sarah A. Bartrama, David A. Lanea, David Smitha, Luis F. A. Teodorob aInstitute for Computational Cosmology, Department of Physics, Durham University, Science Laboratories, South Road, Durham DH1 3LE, U.K. bBAER, Planetary Systems Branch, Space Science and Astrobiology Division, MS: 245-3, NASA Ames Research Center, Moffett Field, CA 94035-1000, U.S.A. Abstract Circular Polarisation Ratio (CPR) mosaics from Mini-SAR on Chandrayaan-1 and Mini-RF on LRO are used to study craters near to the lunar north pole. The look direction of the detectors strongly affects the appearance of the crater CPR maps. Rectifying the mosaics to account for parallax also significantly changes the CPR maps of the crater interiors. It is shown that the CPRs of crater interiors in unrectified maps are biased to larger values than crater exteriors, because of a combination of the effects of parallax and incidence angle. Using the LOLA Digital Elevation Map (DEM), the variation of CPR with angle of incidence has been studied. For fresh craters, CPR ∼ 0:7 with only a weak dependence on angle of incidence or position interior or just exterior to the crater, consistent with dihedral scattering from blocky surface roughness. For anomalous craters, the CPR interior to the crater increases with both incidence angle and distance from the crater centre. Central crater CPRs are similar to those in the crater exteriors. CPR does not appear to correlate with temperature within craters. Furthermore, the anomalous polar craters have diameter-to-depth ratios that are lower than those of typical polar craters. -

Workshop on Lunar Crater Observing and Sensing Satellite (LCROSS) Site Selection, P
WORKSHOP PROGRAM AND ABSTRACTS LPI Contribution No. 1327 WWWOOORRRKKKSSSHHHOOOPPP OOONNN LLLUUUNNNAAARRR CCCRRRAAATTTEEERRR OOOBBBSSSEEERRRVVVIIINNNGGG AAANNNDDD SSSEEENNNSSSIIINNNGGG SSSAAATTTEEELLLLLLIIITTTEEE (((LLLCCCRRROOOSSSSSS))) SSSIIITTTEEE SSSEEELLLEEECCCTTTIIIOOONNN OOOCCCTTTOOOBBBEEERRR 111666,,, 222000000666 NNNAAASSSAAA AAAMMMEEESSS RRREEESSSEEEAAARRRCCCHHH CCCEEENNNTTTEEERRR MMMOOOFFFFFFEEETTTTTT FFFIIIEEELLLDDD,,, CCCAAALLLIIIFFFOOORRRNNNIIIAAA SSSPPPOOONNNSSSOOORRRSSS LCROSS Mission Project NASA Ames Research Center Lunar and Planetary Institute National Aeronautics and Space Administration SSSCCCIIIEEENNNTTTIIIFFFIIICCC OOORRRGGGAAANNNIIIZZZIIINNNGGG CCCOOOMMMMMMIIITTTTTTEEEEEE Jennifer Heldmann (chair) NASA Ames Research Center/SETI Institute Geoff Briggs NASA Ames Research Center Tony Colaprete NASA Ames Research Center Don Korycansky University of California, Santa Cruz Pete Schultz Brown University Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 LPI Contribution No. 1327 Compiled in 2006 by LUNAR AND PLANETARY INSTITUTE The Institute is operated by the Universities Space Research Association under Agreement No. NCC5-679 issued through the Solar System Exploration Division of the National Aeronautics and Space Administration. Any opinions, findings, and conclusions or recommendations expressed in this volume are those of the author(s) and do not necessarily reflect the views of the National Aeronautics and Space Administration. Material in this volume may be copied without restraint for -
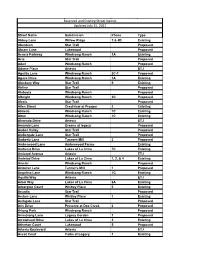
Reserved and Existing Street Names Updated July 15, 2021
Reserved and Existing Street Names Updated July 15, 2021 Street Name Subdivision Phase Type Abbey Lane Willow Ridge 3 & 4B Existing Aberdeen Star Trail Proposed Abram Lane Lakewood Proposed Acacia Parkway Windsong Ranch 1A Existing Acie Star Trail Proposed Adair Windsong Ranch Proposed Adams Place Artesia ETJ Agarita Lane Windsong Ranch 2C-1 Proposed Agave Drive Windsong Ranch 1A Existing Ainsbury Way Star Trail 9 Existing Airline Star Trail Proposed Alabasta Windsong Ranch Proposed Albright Windsong Ranch 3C Proposed Alexis Star Trail Proposed Allen Street Crestview at Prosper 2 Existing Almeda Windsong Ranch 1C Existing Alton Windsong Ranch 1C Existing Alvarado Drive Artesia ETJ Amanda Lane Greens at legacy Proposed Amber Valley Star Trail Proposed Ambergate Lane Star Trail Proposed Amberly Lane Tanners Mill 2 Proposed Amberwood Lane Amberwood Farms Existing Amherst Drive Lakes of La Cima 7C Existing Amistad Avenue Artesia ETJ Amistad Drive Lakes of La Cima 1, 2, & 4 Existing Amsler Windsong Ranch Proposed Andover Lane Tanner's Mill 1 Proposed Angelina Lane Windsong Ranch 1C Existing Aquilla Way Artesia ETJ Arbol Way Lakes of La Cima 6A Existing Arborglen Court Whitley Place 5 Existing Arcadia Star Trail Proposed Arches Lane Whitley Place 1 Existing Archgate Lane Star Trail Proposed Aris Drive Preserve at Doe Creek 2 Proposed Arlong Park Windsong Ranch Proposed Armstrong Lane Legacy Garden 1 Proposed Arrowhead Drive Lakes of La Cima 3 Existing Atherton Court Lakewood 5 Proposed Artesia Boulevard Artesia ETJ Ascot Court Parks at Legacy -

A Multispectral Assessment of Complex Impact Craters on the Lunar Farside
Western University Scholarship@Western Electronic Thesis and Dissertation Repository 2-15-2013 12:00 AM A Multispectral Assessment of Complex Impact Craters on the Lunar Farside Bhairavi Shankar The University of Western Ontario Supervisor Dr. Gordon R. Osinski The University of Western Ontario Graduate Program in Planetary Science A thesis submitted in partial fulfillment of the equirr ements for the degree in Doctor of Philosophy © Bhairavi Shankar 2013 Follow this and additional works at: https://ir.lib.uwo.ca/etd Part of the Geology Commons, Geomorphology Commons, Physical Processes Commons, and the The Sun and the Solar System Commons Recommended Citation Shankar, Bhairavi, "A Multispectral Assessment of Complex Impact Craters on the Lunar Farside" (2013). Electronic Thesis and Dissertation Repository. 1137. https://ir.lib.uwo.ca/etd/1137 This Dissertation/Thesis is brought to you for free and open access by Scholarship@Western. It has been accepted for inclusion in Electronic Thesis and Dissertation Repository by an authorized administrator of Scholarship@Western. For more information, please contact [email protected]. A MULTISPECTRAL ASSESSMENT OF COMPLEX IMPACT CRATERS ON THE LUNAR FARSIDE (Spine title: Multispectral Analyses of Lunar Impact Craters) (Thesis format: Integrated Article) by Bhairavi Shankar Graduate Program in Geology: Planetary Science A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy The School of Graduate and Postdoctoral Studies The University of Western Ontario London, Ontario, Canada © Bhairavi Shankar 2013 ii Abstract Hypervelocity collisions of asteroids onto planetary bodies have catastrophic effects on the target rocks through the process of shock metamorphism. The resulting features, impact craters, are circular depressions with a sharp rim surrounded by an ejecta blanket of variably shocked rocks. -

Curriculum Vitae
Kevin R. Evans, Ph.D. – Curriculum Vitae Geography, Geology, and Planning Department 1733 S. Fairway Ave. Missouri State University Springfield, Missouri 65804 901 S. National Ave. Home: (417) 888-0288 Springfield, Missouri 65897 Cell: (417) 496-0811 Office: Temple 369-A Core lab: 126A Kemper Hall Tel.: (417) 836-5590 Core lab tel.: (417) 836-8855 Lab: (417) 836-3231 [email protected] Fax: (417) 836-6006 http://geosciences.missouristate.edu/kevinevans.aspx Education: Ph.D., honors, Geology, 1997, The University of Kansas, Lawrence, Kansas. M.S., honors, Geology, 1989, The University of Kansas, Lawrence, Kansas. B.S., cum laude, Geology, 1986, Southwest Missouri State University, Springfield, Missouri. Emphases/Principal Interests: Impact geology, stratigraphy, sequence stratigraphy, carbonate depositional systems, geologic mapping, and cultural geology. Professional Certification Registered Geologist (RG), State of Missouri (via ASBOG FG/PG examinations), license no. 2009026258 Teaching Experience: Professor of Geology. Missouri State University, 2013-present. Courses: Physical Geology, Historical Geology, Petroleum Geology, Depositional Environments, Directed Field Trips, and Special Topics. Associate Professor of Geology and Earth Science Education Program Coordinator. Missouri State University, 2008-2013. Courses: Physical Geology, Environmental Geology, Historical Geology, Petroleum Geology, Directed Field Trips, Science Education, Earth Science Education, Pistol Marksmanship, and Special Topics. Assistant Professor of Geology and Earth Science Education Program Coordinator. Missouri State University, 2003-2008. Courses: Environmental Geology, Directed Field Trips, Science Education, Earth Science Education, and Special Topics. Lecturer and Adjunct Faculty Member, Southwest Missouri State University, Springfield, Missouri, 2002-2003. Courses: Global Issues, Environmental Geology, and Physical Geology labs. Instructor, De Anza College, Cupertino, California, Fall Quarter 1997.