Models Scientific Electronic Calculators Owners Manual
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Implementation and Design of Calculator
Implementation and Design of Calculator Submitted To: Sir. Muhammad Abdullah Submitted By: Muhammad Huzaifa Bashir 2013-EE-125 Department of Electrical Engineering University of Engineering and Technology, Lahore Contents Abstract ........................................................................................................................................... 2 Introduction ..................................................................................................................................... 3 Input Unit: ................................................................................................................................... 3 Processing Unit: .......................................................................................................................... 3 Output Unit: ................................................................................................................................ 3 Interfacing and Implementation ...................................................................................................... 4 LCD: ........................................................................................................................................... 4 Hardware Interfacing: ............................................................................................................. 4 Problem and Solution of hardware interfacing: ...................................................................... 4 Software Interfacing: ............................................................................................................. -
Computing Systems
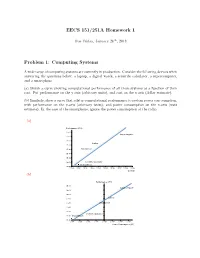
EECS 151/251A Homework 1 Due Friday, January 26th, 2018 Problem 1: Computing Systems A wide range of computing systems are currently in production. Consider the following devices when answering the questions below: a laptop, a digital watch, a scientific calculator, a supercomputer, and a smartphone. (a) Sketch a curve showing computational performance of all these systems as a function of their cost. Put performance on the y-axis (arbitrary units), and cost on the x-axis (dollar estimate). (b) Similarly, show a curve that relates computational performance to system power con- sumption, with performance on the y-axis (arbitrary units), and power consumption on the x-axis (watt estimate). In the case of the smartphone, ignore the power consumption of the radio. (a) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! 1.E+02! Scientific Calculator! Digital Watch! 1.E+00! 1.E+00! 1.E+01! 1.E+02! 1.E+03! 1.E+04! 1.E+05! 1.E+06! 1.E+07! 1.E+08! 1.E+09! Cost ($)! (b) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! Scientific Calculator! 1.E+02! Digital Watch! 1.E+00! 1.E-08! 1.E-06! 1.E-04! 1.E-02! 1.E+00! 1.E+02! 1.E+04! 1.E+06! Power Consumption (W)! EECS 151/251A Homework 1 2 Problem 2: Logic Consider the circuit below. -

Samsung Galaxy J3 V J327V User Manual
User guide. User guide. User usuario. Guía del Guía GH68-47432D Printed in USA Galaxy J7_COLL-78600-UG-PO-CVR-6x4-V3-F-R2R.indd All Pages 2/2/17 11:00 AM SMARTPHONE User Manual Please read this manual before operating your device and keep it for future reference. Table of Contents Special Features . 1 Navigation . 28 Side Speaker . 2 Entering Text . 30 Getting Started . 3 Multi Window . 33 Set Up Your Device . 4. Emergency Mode . 35 Assemble Your Device . .5 Apps . 37 Start Using Your Device . 10 Using Apps . 38 Set Up Your Device . 11 Applications Settings . 41 Learn About Your Device . .15 Calculator . 45 Front View . 16 Calendar . 46 Back View . .18 Camera and Video . 49 Home Screen . .19 Clock . 54 VZW_J727V_EN_UM_TN_QB1_031717_FINAL Contacts . 57 Connections . 104 Email . 64 Wi‑Fi . 105 Gallery . .67 Bluetooth . 108 Google Apps . 71 Data Usage . 111 Message+ . .74 Airplane Mode . 113 Messages . .77 Mobile Hotspot . .114 My Files . 82 Tethering . 117 Phone . 84 Mobile Networks . 117 S Health . 94 Location . 118 Samsung Gear . 96 Advanced Calling . .119 Samsung Notes . 97 Nearby Device Scanning . .121 Verizon Apps . 99 Phone Visibility . .121 Settings . 101 Printing . .121 How to Use Settings . 102 Virtual Private Networks (VPN) . .121 Change Carrier . 123 Table of Contents iii Data Plan . 123 Smart Alert . 133 Sounds and Vibration . 124 Display . 134 Sound Mode . 125 Screen Brightness . 135 Easy Mute . 125 Screen Zoom and Font . 135 Vibrations . 125 Home Screen . 136 Volume . 126. Easy Mode . 136 Ringtone . .127 Icon Frames . .137 Notification Sounds . 128 Status Bar . .137 Do Not Disturb . 128 Screen Timeout . -
Calculating Solutions Powered by HP Learn More
Issue 29, October 2012 Calculating solutions powered by HP These donations will go towards the advancement of education solutions for students worldwide. Learn more Gary Tenzer, a real estate investment banker from Los Angeles, has used HP calculators throughout his career in and outside of the office. Customer corner Richard J. Nelson Learn about what was discussed at the 39th Hewlett-Packard Handheld Conference (HHC) dedicated to HP calculators, held in Nashville, TN on September 22-23, 2012. Read more Palmer Hanson By using previously published data on calculating the digits of Pi, Palmer describes how this data is fit using a power function fit, linear fit and a weighted data power function fit. Check it out Richard J. Nelson Explore nine examples of measuring the current drawn by a calculator--a difficult measurement because of the requirement of inserting a meter into the power supply circuit. Learn more Namir Shammas Learn about the HP models that provide solver support and the scan range method of a multi-root solver. Read more Learn more about current articles and feedback from the latest Solve newsletter including a new One Minute Marvels and HP user community news. Read more Richard J. Nelson What do solutions of third degree equations, electrical impedance, electro-magnetic fields, light beams, and the imaginary unit have in common? Find out in this month's math review series. Explore now Welcome to the twenty-ninth edition of the HP Solve Download the PDF newsletter. Learn calculation concepts, get advice to help you version of articles succeed in the office or the classroom, and be the first to find out about new HP calculating solutions and special offers. -

Calculator Policy
CALCULATOR POLICY 1. Examination Candidates may take a non-programmable calculator into any component of the examination for their personal use. 2. Instruction booklets or cards (eg reference cards) on the operation of calculators are NOT permitted in the examination room. Candidates are expected to familiarise themselves with the calculator’s operation beforehand. 3. Calculators must have been switched off for entry into the examination room. 4. Calculators will be checked for compliance with this policy by the examination invigilator or observer. 5. Features of approved calculators: 5.1. In addition to the features of a basic (four operation) calculator, a scientific calculator typically includes the following: 5.1.1. fraction keys (for fraction arithmetic) 5.1.2. a percentage key 5.1.3. a π key 5.1.4. memory access keys 5.1.5. an EXP key and a sign change (+/-) key 5.1.6. square (x²) and square root (√) keys 5.1.7. logarithm and exponential keys (base 10 and base e) 5.1.8. a power key (ax, xy or similar) 5.1.9. trigonometrical function keys with an INVERSE key for the inverse functions 5.1.10. a capacity to work in both degree and radian mode 5.1.11. a reciprocal key (1/x) 5.1.12. permutation and/or combination keys ( nPr , nCr ) 5.1.13. cube and/or cube root keys 5.1.14. parentheses keys 5.1.15. statistical operations such as mean and standard deviation 5.1.16. metric or currency conversion 6. Features of calculators that are NOT permitted include: 6.1. -

The Demise of the Slide Rule (And the Advent of Its Successors)
OEVP/27-12-2002 The Demise of the Slide Rule (and the advent of its successors) Every text on slide rules describes in a last paragraph, sadly, that the demise of the slide rule was caused by the advent of the electronic pocket calculator. But what happened exactly at this turning point in the history of calculating instruments, and does the slide rule "aficionado" have a real cause for sadness over these events? For an adequate treatment of such questions, it is useful to consider in more detail some aspects like the actual usage of the slide rule, the performance of calculating instruments and the evolution of electronic calculators. Usage of Slide Rules During the first half of the 20th century, both slide rules and mechanical calculators were commercially available, mass-produced and at a reasonable price. The slide rule was very portable ("palmtop" in current speak, but without the batteries), could do transcendental functions like sine and logarithms (besides the basic multiplication and division), but required a certain understanding by the user. Ordinary people did not know how to use it straight away. The owner therefore derived from his knowledge a certain status, to be shown with a quick "what-if" calculation, out of his shirt pocket. The mechanical calculator, on the other hand, was large and heavy ("desktop" format), and had addition and subtraction as basic functions. Also multiplication and division were possible, in most cases as repeated addition or subtraction, although there were models (like the Millionaire) that could execute multiplications directly. For mechanical calculators there was no real equivalent of the profession-specific slide rule (e.g. -

Scale Drawings, Similar Figures, Right Triangle Trigonometry
SCALE DRAWINGS, SIMILAR FIGURES, RIGHT TRIANGLE TRIGONOMETRY In this unit, you will review ratio and proportion and solve problems related to scale drawings and similar figures. You will then investigate right triangle trigonometry. You will examine how trigonometry is derived from the angles and sides of right triangles and then apply “trig” functions to solve problems. Proportions Applications of Proportions Scale Drawings and Map Distances Similar Polygons Trigonometric Ratios Table of Trigonometric Ratios Map of Ohio Proportions A ratio is a comparison of two quantities and is often written as a fraction. For example, Emily is on the basketball team and during her first game she made 14 out of 20 shots. You can make a ratio out of shots made and shots attempted. shots made 14 7 == shots attempted 20 10 A proportion is any statement that two ratios are equal. For example, if Rachel is on the same basketball team as Emily, and she made 21 out of 30 baskets, Rachel’s ratio can be written as: shots made 21 7 == shots attempted 30 10 14 21 It can now be said that Emily’s ratio and Rachel’s ratio are equal. To prove this 20 30 we will use the “cross products property”. For all real numbers a, b, c, and d, where b ≠ 0 and d ≠ 0 . ac = if ad= bc bd Let’s take a look at Emily and Rachel’s ratios and use the cross product property to make sure they are equal. 14 21 = 20 30 14×=× 30 20 21 420= 420 true Use cross products to determine if the two ratios are proportional. -

Scientific Calculator Apps As Alternative Tool in Solving
INTERNATIONAL JOURNAL OF RESEARCH IN TECHNOLOGY AND MANAGEMENT (IJRTM) ISSN 2454-6240 www.ijrtm.com SCIENTIFIC CALCULATOR APPS AS ALTERNATIVE TOOL IN SOLVING TRIGONOMETRY PROBLEMS Maria Isabel Lucas, EdD, Pamantasan ng Lungsod ng Maynila, Manila, Philippines [email protected] ABSTRACT Mark Prensky (2001), the originator of the term digital The present 21st century students belong to the post- natives (Generation Y and Z) and digital immigrants, the millennial generation or Gen Z. They are considered predecessors of the millennials, cited that mathematics have to digital natives who have high penchant on ICT gadgets be reengineered to match the characteristics of the 21st century learners: particularly on smartphones which have already formed In math, for example, the debate must no longer be about part of their daily necessities. The teachers who are digital whether to use calculators and computers – they are a part of immigrants may capitalize this by integrating technology the Digital Natives‟ world – but rather how to use them to as a tool for teaching and learning to cater their learning instill the things that are useful to have internalized, from key needs and interests. Free applications are available both skills and concepts to the multiplication tables. We should be for android and iOS operating systems such as scientific focusing on “future math” – approximation, statistics, binary calculator apps. This study verifies whether the use of the thinking. (p.5) mobile application in computing Trigonometry problems is Practically, not all students in the local university where a good alternative to the commonly used handheld this study was conducted can afford to buy the commercial calculators using a quasi-experiment among 50 students of handheld calculator due to its relatively high cost. -

EL-531W Scientific Calculator Operation Guide
SSCCIIEENNTTIIFFIICC CCAALLCCUULLAATTOORR OOPPEERRAATTIIOONN GGUUIIDDEE <W Series> CO NTENTS HOW TO OPERATE Read Before Using Key layout/Reset switch 2 Display pattern 3 Display format 3 Exponent display 4 Angular unit 5 Function and Key Operation O N/O FF, entry correction keys 6 Data entry keys 7 Random key 8 Modify key 9 Basic arithmetic keys, parentheses 10 Percent 11 Inverse, square, cube, xth power of y, square root, cube root, xth root of y 12 10 to the power of x, common logarithm 13 e to the power of x, natural logarithm 14 Factorials 15 Permutations, combinations 16 Time calculation 17 Fractional calculations 18 Memory calculations ~ 19 Last answer memory 20 Trigonometric functions 21 Arc trigonometric functions 22 Hyperbolic functions 23 Coordinate conversion 24 Binary, pental, octal, decimal, and hexadecimal operations (N-base) 25 STATISTICS FUNCTION Data input and correction 26 “ANS” keys for 1-variable statistics 27 “ANS” keys for 2-variable statistics 31 1 H ow to O pe ra te ≈Read B efore Using≈ This operation guide has been written based on the EL-531W , EL-509W , and EL-531W H models. Some functions described here are not featured on other models. In addition, key operations and symbols on the display may differ according to the model. 1 . K E Y L AY O U T 2nd function key Pressing this key will enable the functions written in orange above the calculator buttons. ON/C, OFF key D irect function 2nd function <Power on> <Power off> W ritten in orange above the O N/C key Mode key This calculator can operate in three different modes as follows. -

Online Calculators in the Test Delivery System
Online Calculators in the Test Delivery System 2021–2022 Updated June 29, 2021 Prepared by Cambium Assessment, Inc. Descriptions of the operation of Cambium Assessment, Inc. (CAI) systems are property of Cambium Assessment, Inc. and are used with the permission of CAI. Table of Contents About Calculators in the Test Delivery System ........................................................................................................ 3 Standard Calculator ............................................................................................................................... 3 Scientific Calculator ............................................................................................................................... 3 Full Function Calculator ......................................................................................................................... 3 Accessing the Sample Calculators ............................................................................................................................ 4 Open a Sample Calculator on Windows/Mac/Linux .............................................................................. 4 Open a Sample Calculator on iPads ....................................................................................................... 6 2 About Calculators in the Test Delivery System Students are able to use an online calculator for some grades and subjects of the RISE Assessments as an alternative to handheld calculators, as allowed by the Utah State Board of Education. Starting -

Scientific Calculator Operation Guide
SSCIENTIFICCIENTIFIC CCALCULATORALCULATOR OOPERATIONPERATION GGUIDEUIDE < EL-W535TG/W516T > CONTENTS CIENTIFIC SSCIENTIFIC HOW TO OPERATE Read Before Using Arc trigonometric functions 38 Key layout 4 Hyperbolic functions 39-42 Reset switch/Display pattern 5 CALCULATORALCULATOR Coordinate conversion 43 C Display format and decimal setting function 5-6 Binary, pental, octal, decimal, and Exponent display 6 hexadecimal operations (N-base) 44 Angular unit 7 Differentiation calculation d/dx x 45-46 PERATION UIDE dx x OPERATION GUIDE Integration calculation 47-49 O G Functions and Key Operations ON/OFF, entry correction keys 8 Simultaneous calculation 50-52 Data entry keys 9 Polynomial equation 53-56 < EL-W535TG/W516T > Random key 10 Complex calculation i 57-58 DATA INS-D STAT Modify key 11 Statistics functions 59 Basic arithmetic keys, parentheses 12 Data input for 1-variable statistics 59 Percent 13 “ANS” keys for 1-variable statistics 60-61 Inverse, square, cube, xth power of y, Data correction 62 square root, cube root, xth root 14 Data input for 2-variable statistics 63 Power and radical root 15-17 “ANS” keys for 2-variable statistics 64-66 1 0 to the power of x, common logarithm, Matrix calculation 67-68 logarithm of x to base a 18 Exponential, logarithmic 19-21 e to the power of x, natural logarithm 22 Factorials 23 Permutations, combinations 24-26 Time calculation 27 Fractional calculations 28 Memory calculations ~ 29 Last answer memory 30 User-defined functions ~ 31 Absolute value 32 Trigonometric functions 33-37 2 CONTENTS HOW TO -

Improving Calculus Learning Using a Scientific Calculator
Open Education Studies, 2020; 2: 220–227 Research Article Miriam Dagan*, Pavel Satianov, Mina Teicher Improving Calculus Learning Using a Scientific Calculator https://doi.org/10.1515/edu-2020-0125 received July 2, 2020; accepted September 28, 2020. made possible with calculators. This includes not only the basic computational tools, but also their potential use in Abstract: This article discusses the use of a scientific enhancing conceptual understanding of mathematical calculator in teaching calculus by using representations concepts and approaches, essential for developing of mathematics notions in different sub-languages research and critical thinking by the student. (analytical, graphical, symbolical, verbal, numerical This is very important nowadays, because academic and computer language). Our long-term experience institutions have been dealing with the failure of students shows that this may have a positive and significant effect in the first year of their studies in general and especially on the enhancement of conceptual understanding of in mathematical courses (Lowe and Cook, 2003; Yorke and mathematical concepts and approaches. This transcends Longden, 2004). With technological advances and a large the basic computational uses, and implies a potential flow of students to STEM professions at universities and for real improvement in the learning success, cognitive colleges, there is a constant decline in the mathematical motivation and problem solving skills of the student. basic knowledge of the novice academic students (Gueudet, We illustrate the steps we have taken towards doing this 2013; Bosch, Fonseca & Gascon, 2004). Undergraduate through some examples. students have difficulties in understanding definitions and various representation of mathematical concepts. It is Keywords: scientific calculator; calculus teaching; because teaching and learning in high school is still based different representations; conceptual understanding; more on algorithmic exercises and memorization, rather cognitive motivation.